基于半监督学习和最小二乘支持向量机回归的废旧机电产品再制造成本预测方法研究*
敖秀奕,张旭刚,江志刚,张 华
(武汉科技大学 a.冶金装备及其控制教育部重点实验室;b.机械传动与制造工程湖北省重点实验室,武汉 430081)
0 引言
废旧机电产品虽无法继续服役,但对其再制造加工可将其性能恢复到原始状态甚至超过其最初的性能,同样也可以节约资源,减少环境的污染[1]。然而再制造企业的主要目的是为了盈利,在对废旧产品进行再制造之前,首先要考虑是否有必要对其进行再制造。如果废旧产品再制造的成本比其产生的收益要高或者高于同类新品的制造费用,那么对其进行再制造加工就没有任何必要,只有在再制造企业有利润的前提下,产品才会被再制造,因此对废旧产品再制造成本进行预测非常有必要,同时也是再制造决策的主要依据之一。
关于再制造成本预测的问题,国内外学者进行了广泛的研究。文献[2]运用统计粗糙理论和灰色理论从状态的角度对重载发动机的再制造成本进行了预测;文献[3]从多个方面分析了发动机再制造企业成本核算与成本管理的问题,并探讨了相应的解决办法;文献[4]运用线性归回模型找到了零部件失效类型与再制造成本的关系,并对再制造成本进行了预测;文献[5]提出了一种再制造工艺优化的方法,该方法能够有效提高可靠性,降低成本;文献[6]从产品寿命周期的角度分析了各阶段的再制造成本,并提出了改善再制造成本的措施;文献[7]引入射频识别技术到废品回收中,将RFID技术水平和RFID标签成本作为考虑因素创建了集中和分散的供应链模型,探讨了最优定价策略和RFID的技术水平;文献[8]提出了再制造分类和回收的策略,建立了再制造率与再制造成本之间的函数关系。
上述研究从资源、环境、工艺、技术等方面对再制造成本进行了研究,涉及的方面虽然很广泛,但由于大多数的研究都是采用定性的分析方法或者是函数的回归分析法,这些方法大多泛化能力较差,也难以反映再制造成本的随机性。文献[9]采用BP神经网络对液压缸的再制造成本进行了预测,但该方法的实施需要大量的数据样本作为支撑,样本获取难度较大。文献[10]利用支持向量机对机械式变速箱的再制造成本进行了预测,验证了在样本量较小的前提下,预测精度比BP神经网络更好。
然而实际再制造过程中,废旧零部件的再制造成本获取过程较为复杂,获取大量已知再制造成本的产品信息非常困难,然而大量还未进行再制造的产品信息是可以较容易获得的。考虑本文研究的内容,标准的最小二乘支持向量机所需的已完成再制造的废旧产品的成本信息依然庞大,很难满足其需求,因此本文将半监督思想引入最小二乘支持向量机回归 (least squares support vector regression,LS-SVR) 算法,综合利用少量已完成再制造和大量未完成再制造的废旧机电产品信息,实现再制造成本的准确预测。
1 基于半监督学习和最小二乘支持向量机的再制造成本预测模型
1.1 再制造成本的构成
机电产品再制造大致可分为回收、拆卸、清洗、检测分类、再制造加工、再装配调试、包装等工序[11]。每一道工序都会产生一定的费用或者收入,机电产品再制造的成本由两部分组成:再制造过程中总的支出费用(包括材料费、人工费、燃油等)和废品处理的收入(包括材料直接回收和降价出售等)。再制造过程总成本公式如下:
y=E-I
(1)
式中,y表示再制造过程的总成本,E表示再制造过程总的支出,I表示处理废品的收入。
1.2 再制造成本的影响因素分析
机电产品再制造成本的60%来源于替换的零部件和可再制造零部件的修复,剩下40%的费用主要包括清洗、检测、材料、人工等费用[12]。由此可看出零部件再制造和零部件替换对再制造成本的影响是巨大的。
产品拆卸后得到的可用零部件分为三类:可直接利用的零部件、经再制造加工利用的零部件和直接替换的零部件。每一件产品拆卸得到的零部件的比率不可能完全相同,这将直接导致再制造成本的差异。除此之外,由于废旧零部件失效形式和失效程度的不同,导致其再制造修复的难易程度也不同,因此再制造复杂程度也是影响再制造成本的一个重要因素[13],复杂程度越高成本则越高,因此引入再制造复杂系数Ω来衡量其再制造的难易程度。假设应直接替换的零部件的比率为va,经再制造加工利用的零部件的比率为vb,则可直接利用的零部件的比率为vc=1-va-vb。由于拆卸的零部件中可直接利用的零部件占比很小,故v1,v2是影响再制造成本的主要因素。
通过以上分析,将直接替换的零部件的比率v1,经再制造加工利用的零部件的比率v2和再制造复杂系数Ω作为输入,再制造成本y作为输出,采用半监督最小二乘支持向量机回归算法(semi-supervised learning based on LS-SVR,SLS- SVR)对再制造成本进行预测。
1.3 建立半监督最小二乘支持向量机预测模型
设第i个样本的输入为xi=(via,vib,Ωi),第i个样本的输出量yi表示对应机电产品的实际再制造成本。给定已知再制造成本的样本集L={(x1,y1), (x2,y2), …,(xm,ym)},其中xι∈Rn,yi∈R(i= 1,2,...m),为了找到零部件各类型的比率和再制造复杂系数与再制造成本之间的联系,在高维特征空间利用最小二乘支持向量机建立再制造成本预测的线性回归模型[14],该模型的回归函数可表示为:
f(x)=wT·φ(x)+b
(2)
式(2)中,f(x)为预测的再制造成本,φ(x)作用是将输入空间x(零部件各类型的比率和再制造复杂系数)的三个非线性属性参数映射到高维特征空间,将原样本空间的非线性拟合问题转变为高维特征空间中的线性拟合问题[15]。wT为权值向量,b为偏置。


(3)
式(3)中,ξ=(ξ1,ξ2, …,ξm)T为对应于L的松弛变量,ζ=(ζ1,ζ2, …,ζu)T为对应于U的松弛变量;γ和λ为取正值的正则化调节参数。
为求上述优化问题,对式(3)求其lagrange函数,将约束问题转化为无约束问题:

(4)
式(4)中,拉格朗日乘数α∈R,β∈R。为满足karush-kuhn-tucker(KKT)条件,对上式w,b,ξ,ζ,α,β求偏导,并令其为0,消元去掉w,ξ,ζ,可得到下列线性方程组(矩阵形式):
(5)

求得线性方程组(5)的解为α=(α1;α2; … ;αm),β=(β1;β2; … ;βu;)和b, 则再制造成本预测模型为:
(6)
2 案例及结果分析
2.1 训练样本与测试样本的确定
现以一批某型号废旧变速箱再制造为例,经拆卸、清洗、检测和分类等一系列工序后,得到了每一个变速箱各类型零部件的比率及其再制造复杂系数,一共30组数据。利用这些数据进行训练和测试,其中训练样本中包含10组已经完成再制造的数据和15组未知再制造成本的数据,测试样本为5组已知再制造成本的数据。训练样本数据如表1和表2所示,测试样本数据如表3所示。

表1 训练样本数据集L

表2 训练样本数据集U

表3 测试样本数据集C
2.2 预测结果及分析
为了验证SLS-SVR所建立的模型预测结果更好,引入均方根误差(RMSE)来比较LS-SVR和SLS-SVR的性能。
(7)

在MATLAB 7.0环境下,利用SLS-SVR建立再制造成本预测模型,同时与LS-SVR对比。预测值与相对误差如表4所示。

表4 预测值与相对误差
由表4可知,LS-SVR建立的预测模型仅采用了已知再制造成本的10个样本进行训练,由于数据量太小,导致训练结果相对较差,最大误差达14.32%,平均误差为9.72%,RMSE=82.80;由于SLS-SVR的预测模型将未知再制造成本的样本加入到了训练中,训练数据量更大,其所得的预测成本与实际成本相差更小,最大误差仅为6.19%,平均误差只有4.114%,RMSE=51.25,预测结果更加理想。图2更直观的反映了两种预测模型的预测结果与真实值的差距,SLS-SVR模型的预测结果更好。
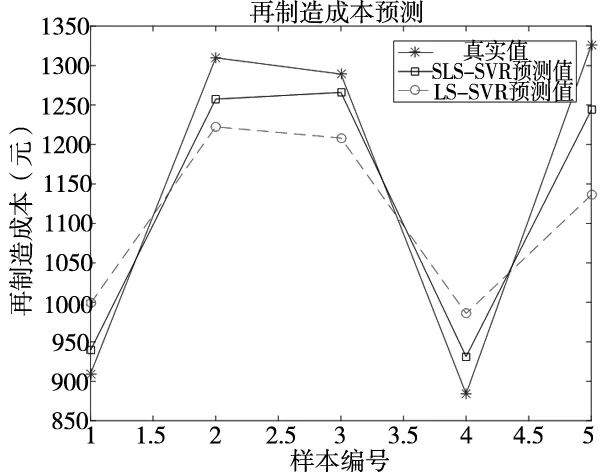
图2 预测结果与实际结果对比图
3 结论
针对再制造非线性、随机性的特性和再制造样本数量少的问题,结合半监督学习与最小二乘支持向量机,以各类型废旧零部件比率和再制造复杂系数为输入,再制造成本为输出建立了废旧机电产品的再制造成本预测模型。案例分析表明,该模型不仅解决了样本量少的问题,而且运算速度快、预测精度高,可为再制造企业快速判断废旧产品的再制造成本和再制造性提供理论依据。

