转子偏心对高速电主轴电磁特性的影响*
邵启鹏,刘保国,冯 伟,申会鹏,张 闯
(河南工业大学 机电工程学院 河南省超硬磨料磨削装备重点实验室,郑州 450001)
0 引言
随着国家制造业水平的不断提高,加工高精密的磨削产品逐渐由传统机床主轴更迭为“零传动”的高速电主轴技术。高速电主轴系统是高维数、多输入—输出和多物理过程的复杂精密设备,其定转子间电磁场的相互作用对电主轴加工性能的优劣起着至关重要的影响。经典的麦克斯韦电磁场理论是电主轴将电能转换成机械能并保证转子高速稳定运转的基础。但是,由于制造误差、安装误差以及砂轮的不均衡受力和温度影响,转子的回转中心会不可避免的相对于定子中心发生偏移。根据轴的旋转中心与定子中心和转子中心的关系,将偏心分为静态偏心,动态偏心和混合偏心。其定义如图1所示,黑点代表转子的旋转中心,定子中心和转子中心分别其圆形的几何中心。偏心会导致气隙间隙不均匀的分布,当绕组通入电流后,由电磁感应原理会产生畸变的气隙磁密。生成的不平衡磁拉力会进一步激发电磁振动[1],对高速电主轴系统的回转精度和高精密加工表面质量以及噪声控制产生消极影响。
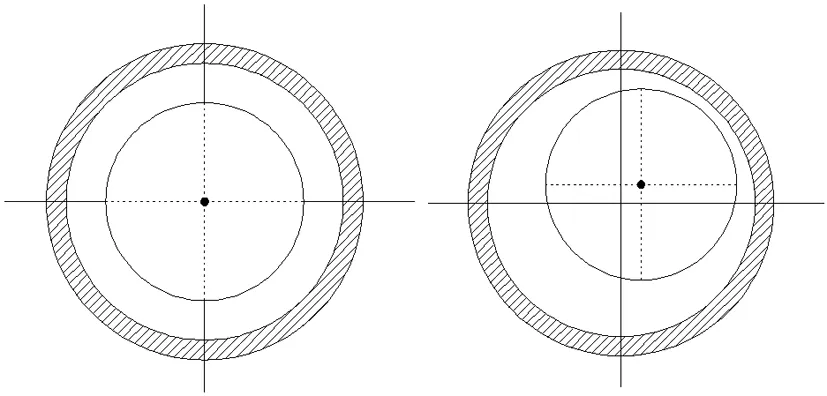
(a) 理想状态 (b) 静态偏心

(c) 动态偏心 (d) 混合偏心 图1 不同类型偏心示意图
由于不平衡电磁力直接影响着主轴的振动和回转精度,很多国内外学者对不均匀气隙厚度和不平衡电磁力已进行了相关的研究[2]。研究成果主要集中于静偏心下不同理论建模的性能分析以及气隙厚度对主轴工作的影响。朱海峰等[3]通过ANSYS结合MATLAB计算了电机静偏心的力波幅值及其分布特征。Belmans[4]推导了电磁力的非线性解析表达式。A Macdonald等[5]提出了一个考虑磁饱和的等效电路新模型。王保民等[6]分析了温升和离心力对定转子气隙厚度的影响。于慎波等[7]发现楔形气隙相比于均匀气隙能使电主轴产生更大的电磁转矩、更小的径向力以及对减小噪声和振动。Jawad Faiz[8]通过研究气隙控制几何条件和扩展非均匀气隙理论对异步电动机进行了精确的电磁建模及性能分析。
虽然学者们对电机理论建模和气隙厚度进行了广泛研究,但对转子不同偏心下电磁力的研究不够深入,本文基于Ansoft软件对电主轴电磁力特性以及相关规律进行了论述,得出了气隙网格控制的一般条件以及不同偏心下气隙磁场的变化规律;研究了电磁力密度随偏心位移的增长趋势。研究结果对电磁振动以及主轴回转精度提供了理论支撑。
1 电主轴气隙磁场分析
1.1 电磁场理论
由电磁学经典理论可知,电磁场是有内在联系的电场和磁场综合作用的结果,一旦了解电磁感应就可以计算预测定转子间的互相作用力。在电主轴通电工作时,磁力线径直地穿过环形气隙,转子高速旋转不断地切割磁力线,并将产生一个径向电磁力以及提供扭矩旋转的切向电磁力。定转子间隙中充斥着复杂的基波、谐波磁场。当转子及其绕组不对中时,利用旋转磁场法将磁通密度表示为磁导率与定子、转子磁动势的乘积已获得的谐波场之和[9]。复杂的磁电激发过程如图2所示。假定在电主轴的定子接线端输入三相正弦电流,首先,定子的通电绕组引起一个磁动势,它由基波磁势和一系列谐波磁势构成,这主要是因为绕组非正弦的空间分布作用。定子磁动势与气隙磁导率综合作用产生定子磁场部分,进而产生定子磁通密度。并且转子导条在这些定子磁通密度中生成电流,其进一步形成了转子磁动势。同理,该转子磁动势与空隙磁导相互作用产生含有其他分量的转子磁密。根据它们的极对数,新的转子磁通密度波可以在定子绕组中引起相应的电流分量,从而建立电流与磁场在气隙空间中的相互联系。
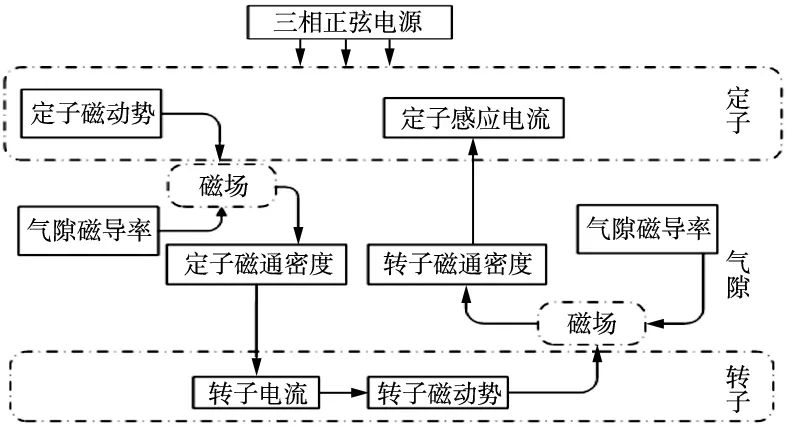
图2 气隙磁场建立示意图
1.2 混合偏心下电磁力的表示
由电机学基本理论可知,高速电主轴各频率、各次数的电磁力波都存在于定转子之间的环形气隙中。气隙中不均衡磁拉力是一个关联因素众多、机理繁杂的产生过程。因此探究气隙电磁力的特性必须进行一定的简化处理,我们可以将转子假设为刚体。电主轴整体磁场大都分布于一个具有包络面的立体空间内,我们可以沿轴向将电主轴切割成多个横截面,将复杂的空间实体问题分解为平面二维问题。
当转子旋转中心相对于定子几何中心发生偏移时,定转子间隙厚度也会随之发生改变,综合气隙厚度不同状态的偏心下是随时间和空间变化的函数。其函数表达式为:
δ(θ,t)=δ0[1-εscosθ-εdcos(θ-ωrt)]
(1)
其中,δ0表示定转子不偏心理想状态时气隙厚度;θ为定子位置角;t是时间;ωr为转子旋转角频率;εs表示静偏心度,εd表示动偏心度,它们分别为静偏移量和动偏移量相对于理想气隙厚度的比值。
由式(1)可知,当εd=0时,电主轴为静偏心状态。此时气隙厚度是一个关于θ的函数,与t无关:
δ(θ)=δ0[1-εscosθ]
(2)
同理,当εs=0时,电主轴为动偏心状态。此时气隙厚度是关于θ和t一起变化的二元函数。
δ(θ,t)=δ0[1-εdcos(θ-ωrt)]
(3)
由现有理论研究可知,气隙中磁感应强度与气隙长度成反比,所以混合偏心下气隙磁导可近似表示为:
λ(θ,t)≈Λ0+Λ0εscosθ+Λ0εdcos(θ-ωrt)
(4)
其中,Λ0为转子旋转中心不偏移下的气隙磁导。
当电主轴通上三相交流电,在电主轴定转子间隙将会产生随时间和空间变化的基波磁动势和定转子谐波磁动势[10]。其综合表达式为:
f(θ,t)=f0(θ,t)+∑fv(θ,t)+∑fμ(θ,t)
(5)
其中,基波磁动势f0(θ,t)、定子v次谐波磁动势fv(θ,t)、转子μ次谐波磁动势fμ(θ,t)为:

(6)
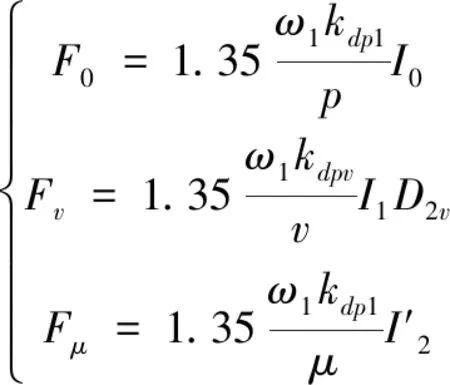
(7)
其中,p为极对数;ω1为基波旋转角速度;ωμ为转子相对定子μ次谐波角速度;Kdpi为基波/谐波绕组因数;D2v为阻尼系数。
由电机工程手册可知,气隙磁通密度的瞬时求解可用式(8)来完成:
b(θ,t)=f(θ,t)λ(θ,t)
(8)
其中,λ(θ,t)为气隙磁导;f(θ,t)为气隙磁动势。
所以可以推出电主轴在混合偏心状况下通入三相正弦电流的气隙磁场函数式:
b(θ,t)=f(θ,t)λ(θ,t)=
[f0(θ,t)+∑fv(θ,t)+∑fμ(θ,t)][Λ0+
Λ0εscosθ+Λ0εdcos(θ-ωrt)]=
[F0cos(pθ-ω1t-φ0)+∑Fvcos(νθ-ω1t-φ1)+
∑Fμcos(μθ-ωμt-φ2)][Λ0+
Λ0εscosθ+Λ0εdcos(θ-ωrt)]=
Bf+Bsh+Bdh
(9)
Bf=B0cos(pθ-ω1t-φ0)+∑Bvcos(νθ-ω1t-φ1)+
∑Bμcos(μθ-ωμt-φ2)
(10)
(11)
(12)
由该公式得出,电主轴气隙磁场是定转子基波磁场和谐波磁场综合作用的结果。Bf是基波磁场磁通密度;Bsh是转子静偏心时谐波磁通密度;Bdh是转子动偏心时谐波磁通密度。
径向气隙磁密比切向气隙磁密大的多,在进行计算时可丢掉切向气隙磁密的影响。依照麦克斯韦电磁场定律,作用于转子上的电磁力正比于气隙磁密的平方,其瞬时求解方程为:
(13)
其中,μ0为空气磁导率,其数值为4π×10-7H/m。
2 建模与仿真
2.1 电主轴的结构参数
文章以磨削高速电主轴为科研依托进行模型分析与数值计算,表1为电主轴的主要结构参数。
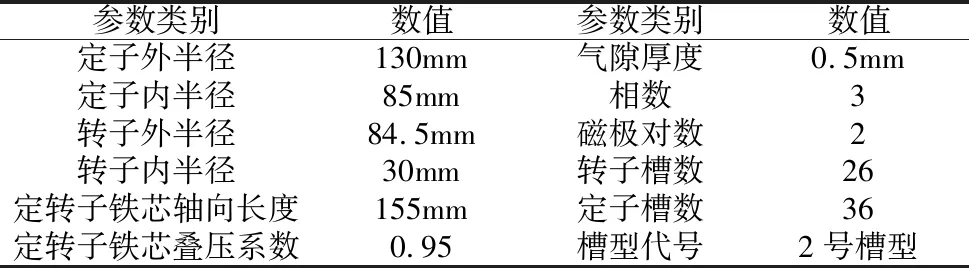
表1 电主轴基本参数
2.2 有限元模型的建立
Ansoft Maxwell是电磁场仿真分析常用的科学软件,它基于经典电磁场理论,采用离散元思维,借助计算机的强大运算能力用模拟仿真替代复杂的模型试验,使实际中繁杂深奥的电磁场问题得以解决[11]。
在电机学中,求解电磁力通常有两种途径,一是麦克斯韦尔应力法,其二是虚功位移法。在具体的应用中,虚功位移法求解较为精确,但只能计算物体总的受力。麦克斯韦尔应力法不仅可以求解物体总的受力还可以求解力的分布,所以本文选取麦克斯韦尔应力法应用在二维有限元电磁场的计算仿真中。使用这种方法,需要在定转子的气隙中画一个首尾相连的圆弧,求解这一曲线上的磁通密度,进而得出电磁力密度,再对曲线路径进行积分乘上模型轴向长度就可以得出电磁力的大小。其计算公式为:
(14)
其中,Br为径向磁通密度,Bt为切向磁通密度,Ld为转子轴向长度。
为了研究偏心状态下电主轴的电磁特性,我们首先绘制了各部件的几何模型,设置了相应部件的材料属性和绕组激励,最终生成所求电主轴二维电磁场模型。在二维电磁场模型中,我们认为定转子铁芯冲片材质均匀且都具有各向同性,其磁化曲线单值。边界条件是在电磁场的求解中也很重要,在这里选择气球边界条件,它在模型磁饱和以及漏磁处理方面具有优势。最终,建立的电主轴电磁场结构模型如图3所示。

图3 电主轴电磁场结构模型
2.3 气隙网格处理
Maxwell中自带的自适应网格剖分方便实用效率高,除此之外软件对精度要求高的操作还提供手动剖分的方式。一般来说,气隙由于运动域Band的存在,即使自适应剖分方式也足以将气隙分为两层。这种方式对分析一般电磁场问题已经足够,但对于电磁力以及电磁转矩等还有一定的缺陷。由于转子受力对于气隙网格的敏感性,所以在计算分析最小气隙处至少需要4层网格,本文划分8层网格,如图4所示。

图4 气隙网格剖分图
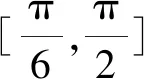
经过数学运算,单元网格的剖分长度最大值D=lmax/h取值范围的表达式为:
其中,d为气隙的厚度,N为要划分网格的层数,一般N=2,4,8,16......。
在网格层数与边长的关系条件中,对气隙层数的控制作用效果良好,相邻的层数剖分并不重叠,相反有一定的缓冲空间。也就是说,在缓冲范围内还会有混合网格的存在。
3 仿真结果的对比
3.1 静态偏心、动态偏心、正常气隙的磁力线图
磁力线云图如图5所示。从图5a中,我们可以观察到均匀气隙的磁力线走势图,它们呈现四极闭合。闭合方式在静偏心、动偏心中同样成立,这是电主轴极对数作用的结果。磁力线主要密布在定转子实体冲片及绕组之间,绕组中间几乎没有磁感线穿过,冲片外缘有少量的漏磁。另外,磁感线疏密不均的排布代表着电磁感应强度的强弱,同规格的面积内,磁力线越密集表示磁通量密度越大。在图5b中可以发现,静偏心的磁力线在转子偏向侧比较密集,在转子转动过程中,磁力线不断地根据绕组的移动重建,但密集区域不变。在图5c中,动偏心的磁力线也是在转子偏向侧较密集,但在转子转动磁力线不断重建的过程中,密集区域也随之发生转变。

(a) 均匀气隙磁力线云图

(b) 静偏心磁力线云图
(c) 动偏心磁力线云图 图5 磁力线云图
3.2 电磁力密度场图
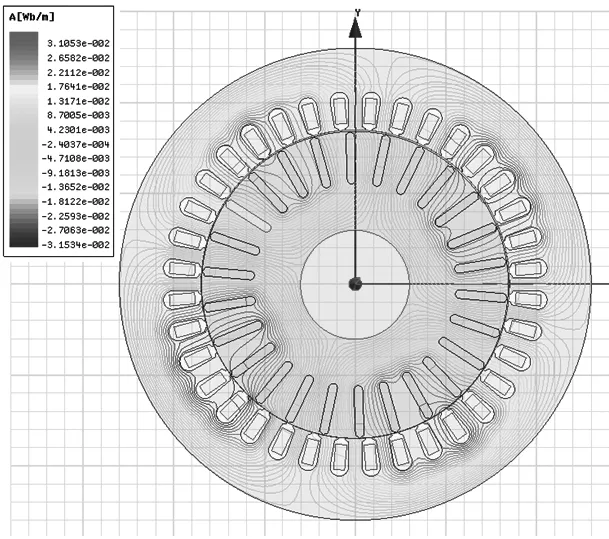
从图6中我们可以得出径向电磁力在圆周360°的分布趋势。这些曲线可以发现磁力波性图的局部呈现锯齿状波动,这主要是因为定转子冲片的槽口和齿作用的影响。磁力波在槽口处量值较小几乎为零,在齿部量值较大。电磁力的幅值在一个磁极内呈现类似正弦曲线的规律变化,磁极边缘幅值最小,几乎为零,然后急剧变化,到磁极中心幅值最大。
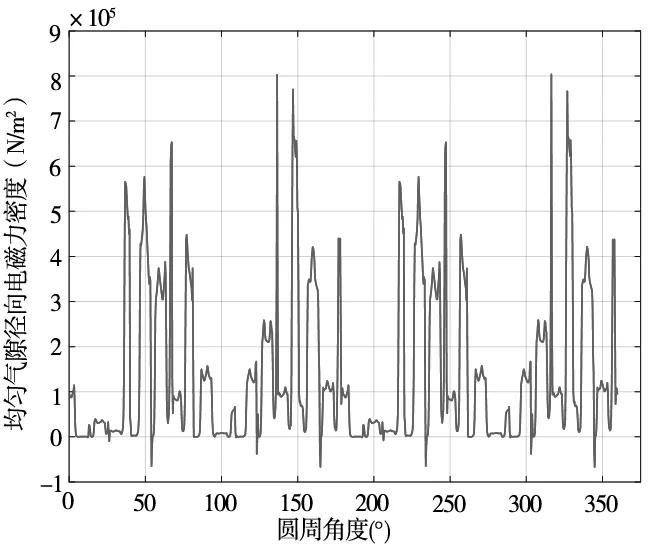
(a) 均匀气隙径向电磁力密度场图
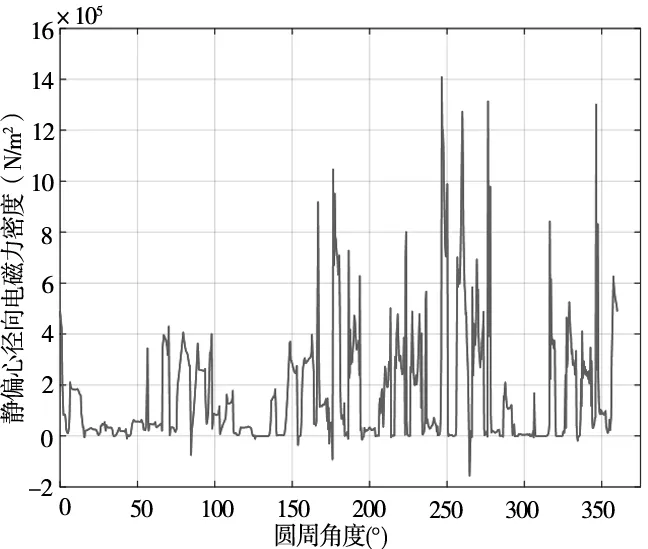
(b) 静偏心径向电磁力密度场图
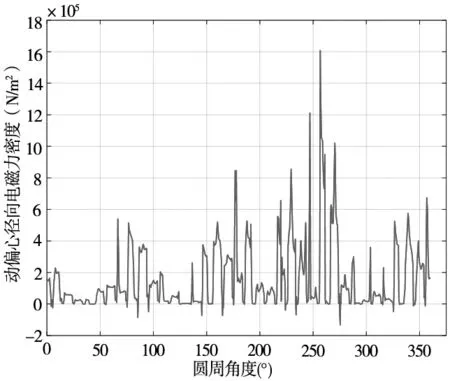
(c) 动偏心径向电磁力密度场图 图6 径向电磁力密度场图
图6a中当转子处于不偏心的正常气隙时,电磁力变化趋势基本相同,幅值规律的波动,对应位置基本相等。图6b静偏心时,电磁力波幅值在磁极与偏移的综合作用下变化明显,偏向侧数值增大,偏离侧则相反。图6c动偏心时,电磁力波幅值呈现动态变化,幅值大小交替改变,幅值差距明显。不同的气隙偏心中,电磁力波形图在两磁极过渡部分几乎不随变化发生改变,这种现象是因为此处与转子偏移相垂直,间隔随偏心位移的变化较小,磁通量密度变化不大造成的。
3.3 不同偏心下最大径向电磁力密度
从图7可以看出,转子动、静偏心最大径向电磁力密度在随偏离位移增大的变化趋势。在不同的偏离量下,不同的气隙偏心下径向电磁力随着转子偏离量递增。在相同的偏离量下,静偏心的不均衡磁拉力变化程度相比动偏心的变化更大, 并且当偏心率较小时,静偏心的不平衡电磁力密度增长更快;动偏心下不平衡电磁力密度在偏心位移不大时缓慢增加,当偏心率较大时,增速较快。
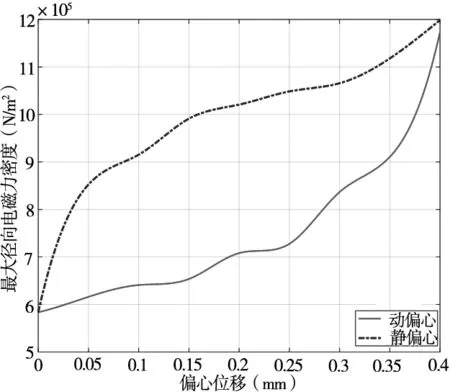
图7 不同偏心下动、静偏心最大径向电磁力密度对比
3.4 动偏心电磁力谐波分析
当相对偏心距较小时以及磁极数大于等于4的情况下,转子的轨迹基本是一个类似圆,与动态偏心的情况一致,所以研究动态偏心非常有意义[12]。磁密是电磁力的直接影响因素,可以通过磁密谐波分析来反映电磁力的谐波占比。
从图8快速傅里叶变换图中,我们可以发现谐波幅值随谐波次数的大致变化规律。气隙磁密的高次谐波幅值比较小,对定转子的作用力很小,因此,在必要条件下可以忽略。由图8a和图8b标记点数值可知,奇数次的谐波占比多余偶数次的谐波,幅值更大。对电主轴电磁力特性起主要作用的是奇数、低次谐波。并且从图中可知,切向磁密的幅值远远小于径向磁密的幅值,这是因为气隙中磁力线基本都径向穿过环形气隙的。
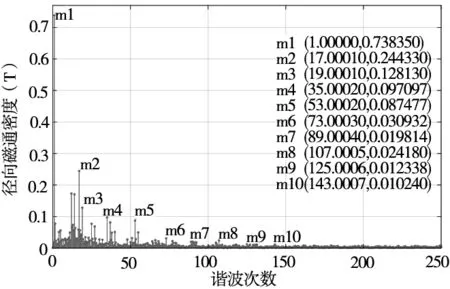
(a) 径向磁通密度FFT分解
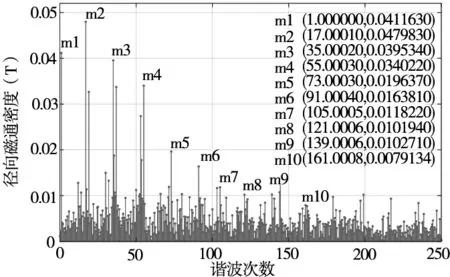
(b) 切向磁通密度FFT分解 图8 磁通密度傅里叶分析图
4 结论
本文将理论推导和Maxwell应力张量法应用到电主轴二维电磁场仿真模型中,研究了不同偏心下气隙磁场和偏心磁拉力的变化规律,得到了以下结论:
(1)基于网格三角形的数值计算,给出了在Maxwell中控制气隙层数的条件,得出了气隙厚度和层数的函数关系,使网格剖分操作更加的简洁并便于控制。
(2)通过对比不同偏心下磁力线和电磁力密度的分布,分析了静偏心和动偏心下电磁分布力的变化规律。不平衡电磁力方向与偏心位移方向相反,电磁力大小在偏向侧显著增大,偏离侧显著减小,且动偏心的增大趋势更加明显。
(3)研究了径向电磁力密度随偏心位移的变化规律。结果表明,随偏心位移的增加,静偏心最大径向电磁力密度变化在偏心率小时增速快,而后增速减慢;动偏心变化规律则相反。总体不平衡电磁力随偏心的增大而增大,力的方向指向圆心。并且在磁通密度的FFT变换中通过具体的数值结果表明了对电磁力起主要作用的是径向、奇数、低次谐波。

