基于中心点法的井下巷道锚杆支护可靠性分析

李 健，郭忠平，郭嘉兴

（1.山东科技大学 研究生院，山东 青岛 266590；2.六盘水师范学院 矿业与土木工程学院，贵州 六盘水 553004）

锚杆支护技术的出现已经超过百年，井下巷道锚杆支护在我国的井工开采的矿山中已经普遍应用，关于巷道锚杆支护的研究也相当的广泛，主要是针对支护效果及支护稳定性进行了大量研究[1-18]。例如康红普[1]等主要研究了预应力锚杆对巷道围岩的加固效果，分析了预应力对巷道支护稳定性的作用。顾士坦[2]详细分析了锚杆的受力特征及锚杆对锚固围岩的加固作用。然而，由于岩石介质的复杂性和各个参数的不确定性，以及在施工过程中的人为误差引起的锚杆支护可靠性问题研究一直未能得到重视，相对于结构工程的可靠性研究，井下巷道锚杆支护的可靠性研究文献并不丰富。例如，王卫军[3]利用验算点法进行迭代计算了巷道支护的可靠性，但仅对间排距和应变2个量对可靠度影响作了简要分析。侯晓琳[4]利用将优化求解法、蒙特卡洛法综合对巷道可靠性进行了研究，但研究方法复杂，在目前实际的工程设计利用该方法有较大难度。目前，在我国采矿行业中，井下巷道的生产设计，往往还是依靠设计手册中的锚杆悬吊理论来进行设计，由于其计算方法简单明了，具有较强的实用性所以至今仍被广泛应用。但利用简单实用的中心点法对悬吊理论设计的支护方案的可靠性问题方面的研究明显偏少，对于此问题应当给予足够的重视。为此重点从概率角度出发，利用中心点法，对采用悬吊理论设计的巷道锚杆支护方案进行可靠性研究，并对多个锚杆支护参数的敏感性进行分析。

1 锚杆支护结构力学模型

锚杆悬吊理论[5-8]是最早出现的锚杆支护设计原理，尽管其具有很大的局限性，但因其计算方便实用，一直广泛应用在工程领域。该理论认为锚杆的作用就是将顶板松散软弱的岩层悬吊在上层稳定的岩层中，保证整个巷道的稳定，悬吊理论模型图如图1。

图1 锚杆支护悬吊理论模型图

设松散层高度为H，锚杆的间排距为a，有：

锚杆的锚固力Q1：

式中：σt为锚杆抗拉强度，MPa；d为锚杆直径，mm。

悬吊的松散层质量Q2：

式中：H为松散层高度，m；a为锚杆的间排距，m；ρ为岩层平均密度，t/m3。

2 锚杆支护结构可靠性分析

2.1 中心点法

中心点法属于一次可靠度方法中的均值一次二阶矩法MFOSM[9]。均值一次二阶矩法首先用Taylor公式将非线性功能函数展开，选在随机变量的均值点即中心点μxi处。

假设某结构的功能函数为：

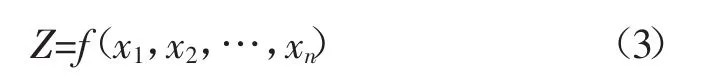
式中：xi为随机变量（i=1，2，…，n）。

在随机变量xi的均值μxi处展开，略去高次项，保留线性项可得：

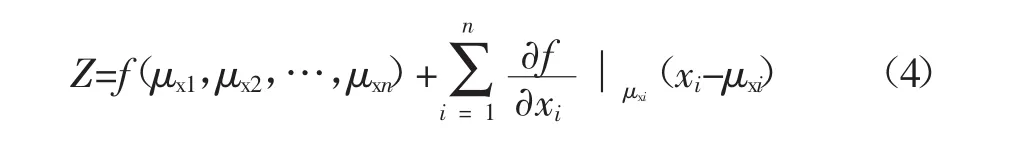
式中：μxi为随机变量 xi的均值（i=1，2，…，n）。

结构的可靠度指标β可表示为：

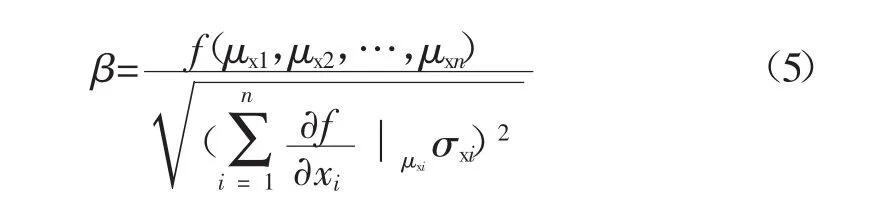
式中：μxi为随机变量 xi的均值（i=1，2，…，n）；σxi为随机变量xi的标准差。

结构的可靠度概率pr和失效概率pf可表示为：

式中：pr为结构的可靠度概率；pf为结构的失效概率；Φ为标准正态分布函数。

2.2 锚杆支护结构功能函数方程

锚杆的间排距a，在认为安装锚杆时候，由于误差的存在，使得a存在一定的随机性。同时，由于松散层的高度H只能是估算，不可能准确的测量，所以H也存在较大的随机性。一般，一个正常矿井的锚杆作业施工队伍的施工水平是较为稳定的，所以在安装锚杆时，由于人为误差引起的锚杆间排距a的随机性也应具有一定的统计规律。为方便研究，将a和H 2个变量都假设服从正态分布，他们的期望和标准差都分别记为 μH、μa、σH、σa其余的变量例如锚杆直径d、锚杆抗拉强度σt、岩层平均密度ρ都记为常数。仅考虑2个变量，有锚杆支护结构功能函数方程：

式中：Q1为锚杆的锚固力；Q2为悬吊的松散层质量。

极限状态方程为：

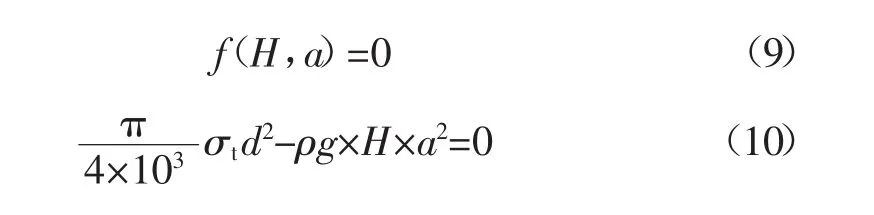
式中：各个参数含义同式（1）和式（2）。

由中心点法式（5）计算得可靠性指标：

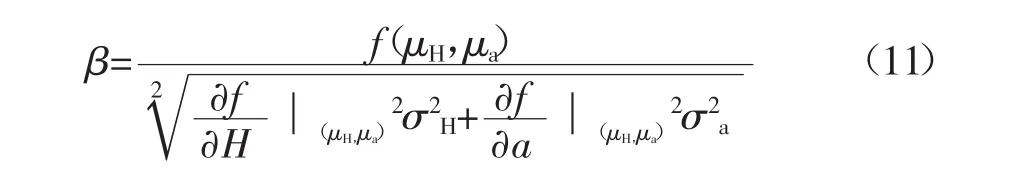
整理得，

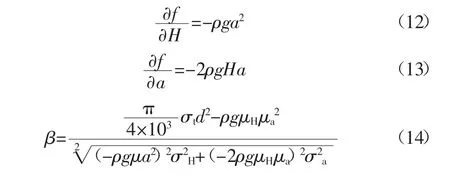
式中：σt为锚杆抗拉强度，MPa；d为锚杆直径，mm；H为松散层高度，m；a为锚杆的间排距，m；ρ为岩层平均密度，t/m3；σH为松散层高度H的标准差，m；σa为锚杆间排距a的标准差，m。

2.3 支护结构可靠度计算

根据某矿井下巷道的实测取值如下，锚杆抗拉强度σt=200 MPa，锚杆直径d=20 mm；松散层高度H=0.5 m；锚杆的间排距a=1.5 m；岩层平均密度ρ=3.0 t/m3；松散层高度H的标准差σH=0.26 m；锚杆间排距a的标准差σa=0.2 m。

将上述数值代入式（14），计算得:

代入式（6）和式（7），得结构的可靠度概率为:

支护结构的失效概率为:

即支护结构的失效概率为6.91%，不到7%的失效概率对于一般的井下巷道锚杆支护设计方案是可以接受的[10]。

3 支护参数敏感性分析

可靠性指标β对于这些参数的敏感性是怎样的，下面再来分析一下。令所有的参数在其均值上下±10%范围内取值，每次增减2.5%，得到支护参数变化表（表 1）[11-12]。

表1 支护参数变化表

表1中的参数仅改变其中1个，保持其他参数不变，求得对应的可靠度指标，得到支护参数敏感性分析表（表2）。为分析支护参数的敏感性，依次取上表中其中之1个参数值，和除此参数值之外的剩余参数值的平均值，代入式（14），得到的可靠度指标β，即是该参数变化后的可靠度值，并将该值填入原表对应位置。并依次代入式（14）计算可靠度指标β后填入原表，得到支护参数敏感性分析表。例如，取表中第1个值σt=180 MPa，其余参数值均保持平均值，根据式（14）计算得β=1.162 305，并将该值填入原表对应位置，即表第1行第1列位置。

表2 支护参数敏感性分析表

根据支护参数敏感性分析表，用EXCEL表格，生成的支护参数敏感性分析图如图2。

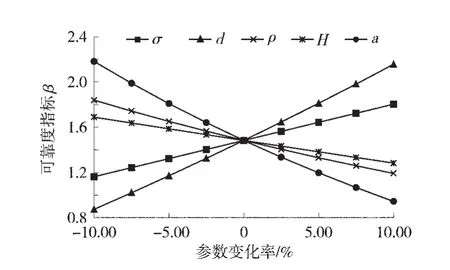
图2 支护参数敏感性分析图

表3 可靠性指标β的最大变化率指标表

根据支护参数敏感性分析表图和可靠性指标β的最大变化率指标表，可知：

1）根据可靠性指标β的最大变化率指标表，可知各个支护参数的敏感性，从大到小排序依次为锚杆直径d、锚杆间排距a、岩层密度ρ、锚杆抗拉强度σt、松散层厚度 H。

2）在其他参数不变条件下，可靠性指标β与锚杆间排距a，岩层密度ρ，松散层厚度H，呈负相关关系，即这些参数数值越大，支护方案的可靠性就越低。可靠性指标β与锚杆直径d，锚杆抗拉强度σt为正相关关系，即参数数值越大，支护方案的可靠性越高。

3）具体每个参数的敏感性是不一样，即对可靠性指标β的影响程度是不同的。最为敏感的是锚杆直径d和锚杆间排距a。在同样条件下，锚杆直径d仅从20 mm减少到18 mm，可靠性指标β就从1.482 63降低到0.874 0，对应的可靠性概率pr即从93.09%，降低到80.89%。对于这样支护方案可靠性明显偏低。同样锚杆间排距a，从1.50 m增加到1.65 m时，可靠性概率就变为82.74%，也是不能接受的可靠度。

4）根据文献[13]来看，要求锚杆安装间排距a误差为±100 mm，这个变化范围对于锚杆间排距a=1.0 m的设计方案来讲，变化幅度已经达到10%，以本文中的工程案例来分析，锚杆间排距a降低10%后，β即从1.482 63降为0.944 102，对应的失效概率即从93.09%降为82.74%，这样对支护结构的可靠度就会产生显著影响[14]。

4 结论

1）锚杆间排距a对支护结构的可靠度有显著影响。在实际巷道锚杆支护中，锚杆间排距a受人为影响因素大，常出现与设计间排距的偏差。所以，在比较重要的巷道支护设计中，方案的最终确定时，应充分考虑本矿井的实际情况和施工队伍水平，有意识的调整设计方案，采取冗余设计，确保方案的可靠性。

2）支护结构的可靠度对锚杆直径d最为敏感，要充分考虑实际工程中锚杆直径d受各种因素（锈蚀）引起的减小问题。在实际中，锚杆采用标准的型钢，其原始参数是比较均匀的。一般合格的型钢尺寸误差都在百分之一左右，不会出现10%这样的误差，所以在支护结构使用初期，直径d的影响并不显著。但由于井下巷道往往环境恶劣，如锚杆在围岩中会发生锈蚀，造成锚杆有效直径的减小。同时，现在井下巷道支护设计中普遍采用的高强度和小直径锚杆支护设计方案，锚杆的锈蚀速度与锚杆的应力状态有关，工作应力越大，锈蚀的速率越快。这样如采用小直径的锚杆，锈蚀引起的有效直径减小问题更加明显，进而降低整个锚杆支护系统的可靠性。这些方案在初期和短时间内，可靠性降低问题并不明显，所以在大量服务年限较短的采准巷道中使用尚未见严重问题的发生，但是这中间还是存在一定的安全隐患。在井下恶劣环境中和使用年限较长的支护工程中，支护方案失效的风险将进一步加大，有可能造成严重的后果。当直径d减少10%时，可靠性就会大幅降低，从而可能引发整个支护系统的失效。