变基床系数条件下充填采煤工作面顶板力学机制分析

冯 超，李广洲，王军伟，崔青原

（1.安阳工学院 土木与建筑工程学院，河南 安阳455000；2.驻马店市建筑勘察设计院有限公司，河南 驻马店463000）

充填采煤条件下，充填体置换煤体的过程存在时间和强度不协调，导致顶板应力重分布，结果可能导致顶板岩层产生较大变形而发生冒顶。获得充填工作面顶板变形及内力分布规律对维持工作面稳定、预测覆岩裂隙扩展高度、关键层变形规律等方面具有重要意义。在目前充填采煤技术条件下，工作面直接顶及基本顶仅发生弯曲变形，所以其力学机制的理论研究主要采用弹性曲梁模型[1]、弹性地基梁、板模型[2-9]等。弹性地基梁模型是将顶板岩梁的支承体视为弹性支座，考虑了梁与支座的变形协调，相比于弹性梁、板模型，更加符合实际工程。目前，在基于弹性地基梁模型的相关理论分析成果丰硕，文献[2-6]分别从不同侧面出发，建立顶板弹性地基梁模型，分别分析了顶板变形，内力的影响因素，工作面下采空区矿压显现，顶板裂隙扩展规律。文献[7-9]考虑不同边界条件，建立顶板弹性地基薄板模型，分别从不同角度，分析了基本顶破断条件及其影响因素、直接顶变形规律。上述研究成果均是基于支承体基床系数为恒定常数，建立整个采场顶板力学模型进行研究，而作为顶板支承体的煤体和充填体基床系数为非恒定常数情况鲜有考虑。考虑工作面前方煤体破碎区基床系数为非恒定常数和充填体基床系数随龄期增长而变化的特征，针对“充-采”循环接续过程中顶板受力最不利情况，建立变基床系数下工作面顶板弹性地基梁模型，得到顶板的变形及弯矩分布图，为工程实践及顶板防控提供理论参考。

1 工程背景

榆阳煤矿首次以风积砂为主要材料，添加水泥、粉煤灰、辅料和水，按照一定比例配置充填料浆，成功进行了风积砂膏体充填采煤的工业化试验[10]。

2307充填工作面北邻2301连采充填工作面，东邻回风巷，南侧为未采区、西侧边界煤柱。工作面宽度为150 m，煤层厚度平均3.5 m，采深平均190 m，煤层顶底板岩层情况见表1。

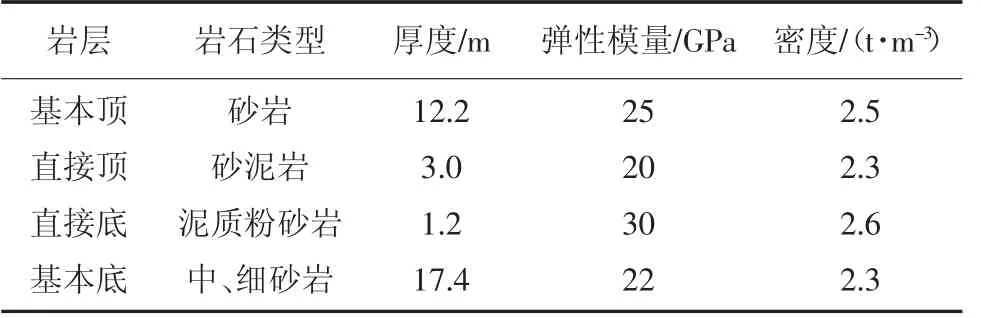
表1 煤层顶底板参数

“充-采”循环作业是在支架的掩护下，前方采煤后方采空区支设柔性模板，充填料浆在地表制备完毕，通过自流充入模板内，达到一定强度后，继续进行下一循环作业，每一循环平均周期为4 d，充填采煤循环作业如图1。

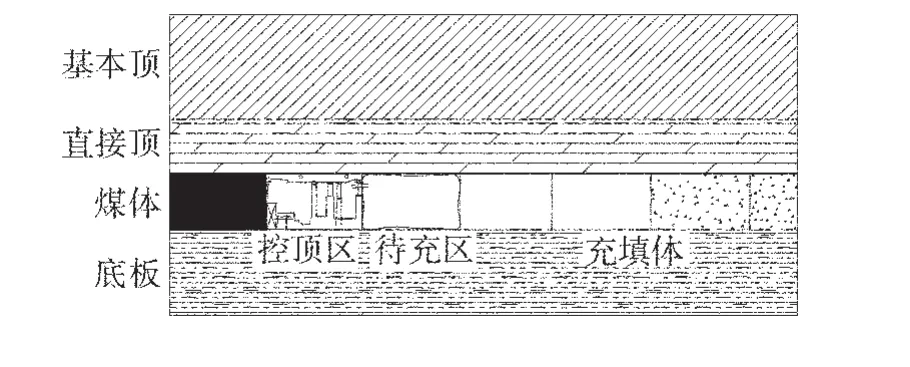
图1 充填示意图

2 充填顶板力学模型

工作面顶板的稳定性是关系到煤矿安全及充填工作面正常进行的关键，由图1可知，当采煤工作面向前采进1个步距后，支架后方采空区尚未充填而上一循环的充填体龄期为1 d，此条件下对顶板的稳定性最为不利。因此，以单位宽度的顶板岩梁为研究对象，其受力模型如图2。

顶板岩梁受力范围共分5段，AB段为煤层破碎区，煤层被采出后，前方煤壁一侧形成自由面，在上部荷载作用下，一定范围内煤体破裂，形成煤体破碎区，在这一范围内，煤体基床系数非恒定值；BC段为支架控顶区，利用液压支架的支承力控制顶板下沉，这一范围内可视为基床系数为常数；CD段为待充区，这一范围内顶板下方未设支承，基床系数为0；DG段为不同龄期条件下的膏体充填体支承区，对顶板的支承作用随时间变化逐渐增长，假设充填材料强度在28 d达到100%，这一范围内的充填体以1个充填步距为单位，基床系数逐渐变化。

将单位充填顶板视为岩梁，底部支承物体可视为连续的弹簧支座，利用Winkler弹性地基梁理论[11]，建立的变基床系数顶板岩梁的弹性地基梁模型如图3。图中a为煤层破碎区宽度，b为控顶区宽度，l为一充填步距宽度，q为岩梁所受上覆岩层压力，kmi为煤层支座的基床系数，kc为控顶区基床系数，kti为第i充-采循环充填体基床系数，kt为充填体恒定基床系数。

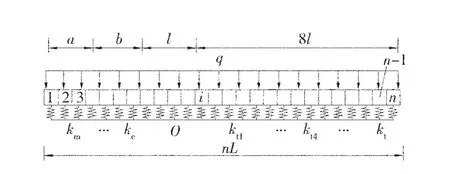
图3 顶板岩梁弹性地基梁模型

考虑到破碎区煤层为非恒定常数、充填体的基床系数随龄期变化，解析法难以获得理论解，可基于有限差分原理[12]进行求解。

将岩梁均分长度大小为L的n个小段，可近似认为每个小段岩梁下地基反力pi为均匀分布，设每段挠曲变形量为yi，则：

式中：ki为各区段不同地基的基床系数。

3 充填顶板变形及内力计算的数值解法

由材料力学可知，梁挠度y与弯矩M的微分关系为：

式中：E为岩梁弹性模量，MPa；I为岩梁截面惯性矩，m4。

根据有限差分原理可知，用中心差分代替二阶导数，即：

将式（3）代入式（2）中可得：

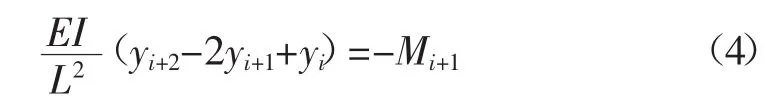
式中：Mi+1为第i+1节点处岩梁弯矩。

将图3中的力学模型岩梁第i+1节点处截开，取左侧为研究对象，按照弯矩平衡原则，可求得第i+1节点处岩梁弯矩Mi+1为：

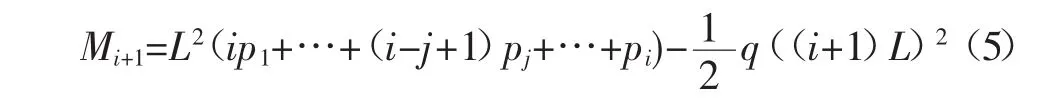
式中：q为岩梁上部均布荷载。

将式（5）写成和式的形式为：

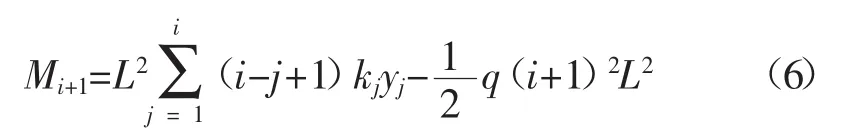
将式（6）代入到式（4）整理并化简可得：

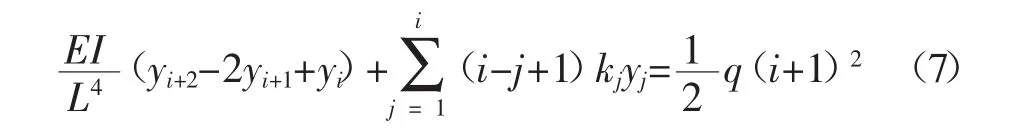
当 i分别取 1，2，…，n-2，上式可以列出 n-2个方程式，仍需要补充2个方程，才能求解全部挠度值。根据全梁下弯矩和竖直方向合力为0为条件，补充另外2个方程：

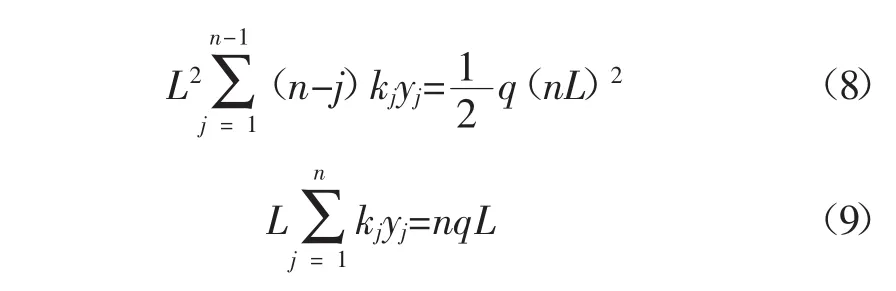
将这n个线性方程式用矩阵表示：

式中：[A]为1个n阶方阵；{Y}为挠度列向量；{P}为荷载向量，其分别可表示为：

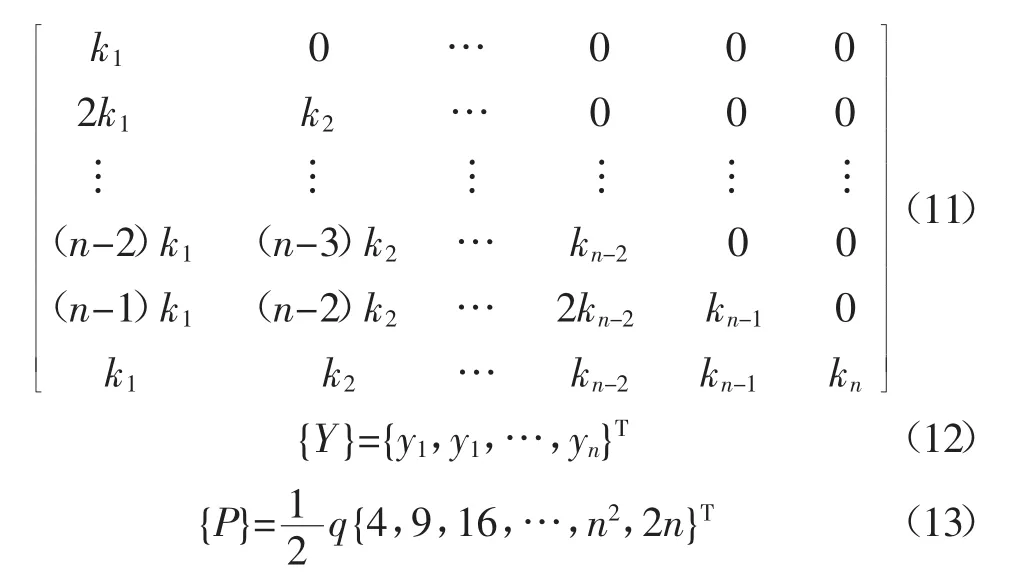
确定各区段的基床系数，即可以求出挠度列向量{Y}。

4 基床系数的确定

4.1 破碎区煤体基床系数

煤体未采出之前处于三向受压状态，被采出后，煤体一侧卸荷，处于自由状态，水平应力被释放，加之上部荷载作用下，浅部煤体向自由面发生水平变形，进而一定范围内产生塑性裂缝和破碎，承载力降低，基床系数也发生变化。基床系数的确定可由现场试验或者经验公式求解[13-14]，但是，破碎区煤体难以进行室内试验，为此，采用数值计算的方法研究km变化规律，基床系数由下式确定[11]。

式中：km为基床系数，MPa/m；q为地基上所受应力值，MPa；s为荷载作用下煤层地基位移，m。

采用FLAC3D软件建立三维煤层模型，模型的尺寸为10 m×10 m×3.5 m，模型上部施加均布荷载∑ρgH=4.56 MPa（ρ为上覆岩层平均密度，H为采场埋深），x=0面、z=3.5面为自由面，其余边界面固定，采用莫尔-库伦强度准则，煤层力学参数见表2，计算出竖向位移如图4。

表2 煤层力学参数

图4 煤层竖直方向位移

由图4可知，在原岩应力作用下，一定范围内煤体竖向位移随至开采面距离的增大而逐渐减小，浅部竖向位移最大，在距离煤壁约0.7hm（hm为煤层厚度，m）后趋于稳定。为简化计算，将一端自由的煤层基床系数简化为折线模型[15]，如图5，图中a=hm·tan（45°-φ/2）≈2.5 m，km0为自由面基床系数，将模拟结果代入式（14），可求出 km0=43 MPa/m，km=460 MPa/m。在（0，a）范围内，km（x）=167x+43，可确定破碎区煤体不同位置的基床系数。

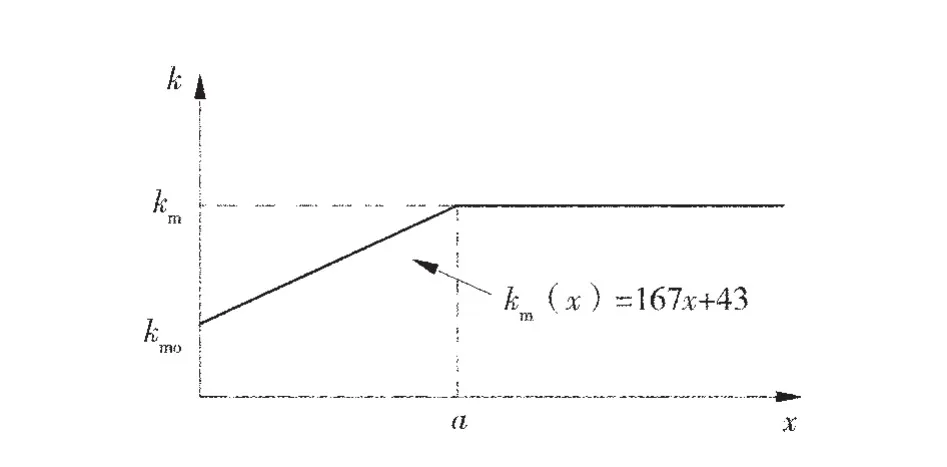
图5 煤层基床系数简化模型

4.2 充填体基床系数

为获得不同龄期条件下充填体的基床系数值，对榆阳煤矿2307工作面不同循环的充填体进行钻心取样。测得的充填体在单轴压缩条件下的力学参数见表3。

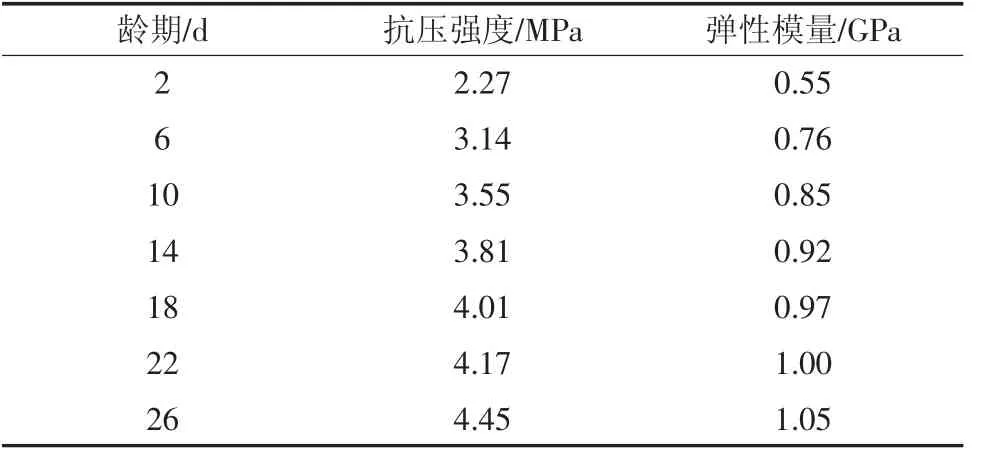
表3 充填体单轴压缩下力学参数

充填体基床系数kt可由下式计算：

式中：E0为充填体弹性模量，GPa；h0为充填体高度，m。

取h0=3.5 m。充填体基床系数随龄期变化曲线如图6，充填体基床系数随龄期增长而变大，龄期在0~10 d范围内，基床系数增长较快，在10~26 d范围内，基床系数增长缓慢，变化趋势基本符合对数变化，拟合方程为：y=68.77ln(x)+82.552。

5 顶板挠度及弯矩分布

5.1 顶板挠度及内力分布

图6 充填体基床系数随龄期变化曲线

根据上述分析及榆阳煤矿2307工作面的实际情况，按照图1工作面位置，取单位宽度岩梁总长为70 m为研究对象，厚度3 m，其中岩梁的弹性模量E=20 GPa，截面惯性矩I=2.25 m4，上覆岩层平均密度ρ=2.4 t/m3，采场埋深H=190 m，则岩梁所受均布荷载q=4.56 MPa，破碎区煤体宽度a=2.5 m，控顶区宽度b=6 m，一个充填步距长度l=6.4 m，控顶区液压支架等效基床系数kc=1.44 MPa/m，煤层破碎区基床系数km及充填体不同龄期对应的基床系数kt按照第4节分析结果取值。计算中将岩梁均等分为140个小段，每个小段长度L=0.5 m，采用有限差分法，计算的岩梁挠度及弯矩的分布曲线如图7和图8。

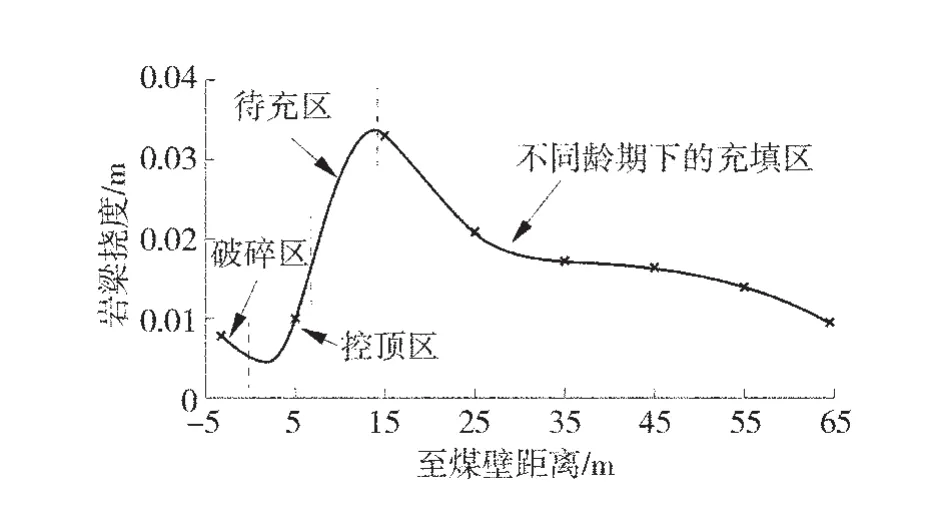
图7 顶板变形分布曲线

图8 顶板弯矩分布曲线

图7 显示破碎区煤层上方岩梁挠度逐渐减小；在控顶区上方，受支架巨大的支承力影响，岩梁挠度最小，最小值为5 mm，在距离煤壁13 m处的待充区上方，顶板岩梁变形量最大，最大值为34 mm；在充填区上方，受充填体支承强度不断增长的影响，岩梁变形量平缓变化。

图8显示顶板岩梁的弯矩在控顶区上方弯矩最大，最大值为180 MN·m，在待充区上方弯矩最小，最小值为-160 MN·m，并随工作面后方长度增加而逐渐降低为0。主要原因是支架巨大支承强度、待充区未及时支承和充填体强度低未形成有效支承。充填顶板在控顶区和待充区范围内弯矩急剧变化，易造成顶板弯剪破坏，引起工作面冒顶事故的发生，对充填工作面的安全产生极大威胁。

5.2 顶板防控措施

1）提高充填体早期弹性模量。待充区后方的充填体早期弹性模量低，未能及时对顶板形成有效支承，可利用柔性模板的滤水功能，将充填料浆多余水分泌出，以提高充填体早期弹性模量。

2）调整充填步距。充填步距大，可提高充填效率，但在未支承状态下，顶板跨度越大，弯矩越大。应加强顶板监测，动态调整充填步距。

3）超前顶板加固。支架向前推进过程中，在架间打设控顶锚杆，利用锚杆拉力，将顶板所受荷载转移至上层岩体。

6 结论

1）破碎区煤体基床系数为非恒定常数，并沿开采方向逐渐增大，距离开采面2.5 m后逐渐稳定，利用数值模拟得到基床系数随距离的变化，并求出简化模型表达式；对不同龄期的充填体开展抗压强度试验，得到充填体基床系数随龄期增长而升高，且符合对数变化特征并拟合出变化的表达式。

2）建立顶板岩梁变基床系数弹性地基梁力学模型，得到顶板挠度和弯矩分布曲线。顶板挠度在控顶区上方最小，在待充区上方最大，随差开采工作面距离增大先增长后逐渐降低。顶板岩梁弯矩在控顶区和待充区上方的变化剧烈，易造成顶板弯剪破坏。