基于驾驶人特性的自适应换道预警算法研究*

刘志强，韩静文，倪 捷

（江苏大学汽车与交通工程学院，镇江 212013）

前言

车道变换是驾驶过程中最常见也是危险程度较高的驾驶行为，美国高速公路安全管理局（national highway traffic safety administration，NHTSA）研究数据表明，由换道引发的交通事故在所有事故中占比高达27%，其中驾驶人因素导致的交通事故约占93%［1］。同时，我国大型实车路试验（China field operational tests，China-FOT）统计数据也进一步显示，换道切入危险事故占事故总量的23.91%［2］。因此，为降低由换道引发的交通事故，改善驾驶人的操作环境，换道预警辅助系统（lane changing warning system，LCWS）得到广泛研究并实际应用［3］。

目前，国内外针对换道预警算法的研究多集中于两方面：一是基于避撞时间（time to collision，TTC）的换道预警［4-5］；二是基于最小安全距离（minimum safety distance，MSD）的条件约束预警［6-7］。前者根据自车与前车相对位置及相对速度的变化情况预估车道变换的潜在风险。后者通过设定最小安全距离阈值及时向驾驶人做出危险警告。由于预警系统的激活可能会与驾驶人操作习惯相悖，导致此类系统接受度低，部分研究人员基于此开展针对驾驶人个体差异性的预警模型研究［8-9］。但大多驾驶人分类模型是离线状态下完成的，运算量大，且模型参数单一固定，预警系统实时性差。基于此，本文中提出一种在线学习驾驶人特性的换道预警算法。首先，搭建算法的框架结构；其次，确定换道危险感知模型，设计模型参数及预警阈值的动态调节算法；最后，通过实车试验，验证算法自适应驾驶人特性的能力及预警策略效果。

1 自适应驾驶人特性的LCWS结构

为使LCWS具有自适应驾驶人特性的能力，设计如图1所示的系统结构。首先，确定换道模型，提出换道参数修正方法实现对多车碰撞风险的综合评估，并给出模型参数的动态调节方法；其次，建立基于驾驶员操作感知的换道行为数据库，设计基于信息熵的最优阈值搜索方法，同时建立阈值合理性评价体系，判断阈值是否需要调整；最后，将实时危险评估值与预警阈值进行比较，判断系统报警情况，使得预警系统在不干涉驾驶员操作的前提下，根据当前状态自我调节，提高行车安全性。

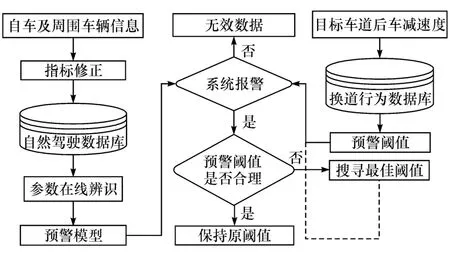
图1 自适应驾驶人特性的LCWS结构

2 自适应换道预警模型

考虑换道过程中周边车辆的行驶状态，综合评价自车行驶危险程度，在模型中引入定量表征多车影响权重的指标，通过动态权重分配方法对换道参数进行修正。此外，为自适应驾驶人特性对模型参数进行在线辨识，实现预警模型的个性化设计。

2.1 换道预警模型

本文中所研究的换道场景为快速道路环境，如图2所示。换道过程为SV车（自车）从原车道变换至目标车道，ALV车和AFV车分别表示目标车道上的前、后车辆，LV车表示同车道上前车，FV车表示同车道上后车。SV车从当前车道换至目标车道的前后车之间。换道过程中，通过车联网环境实现信息交互，获取的车辆状态参数均以自车为参照物。

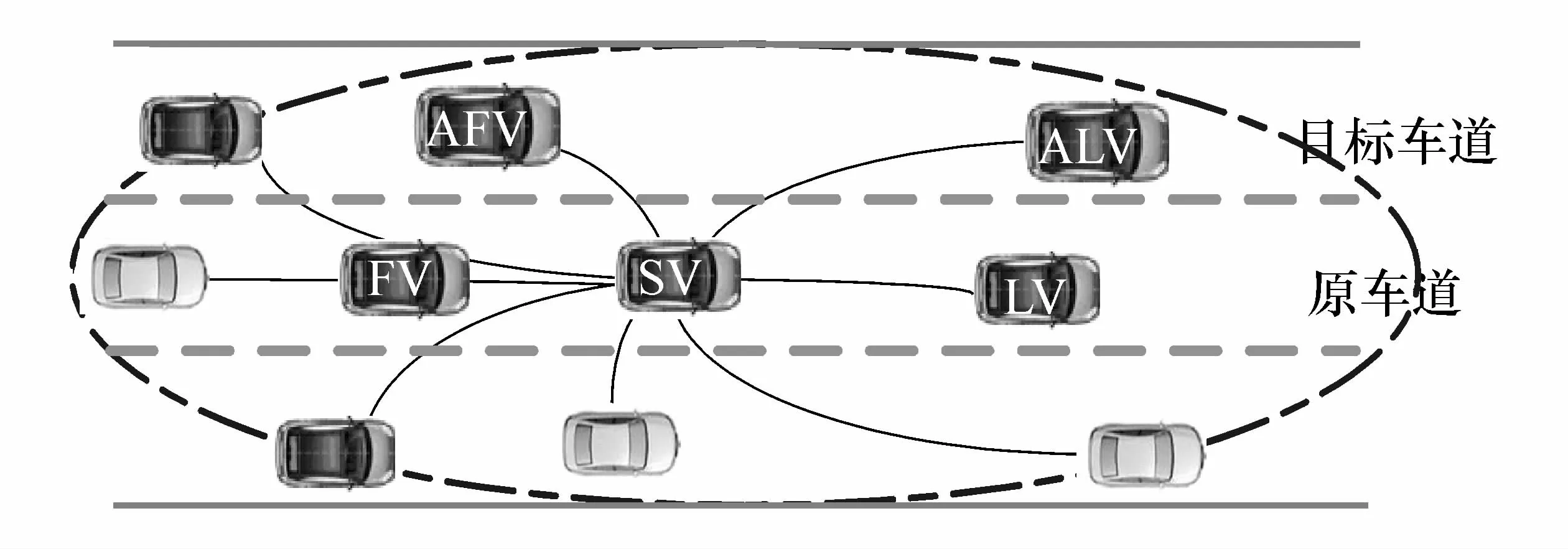
图2 换道场景

基于自车与前车保持安全距离的假设，虚拟弹簧理论［10］将行车队列中的驾驶人期望加速度（t）描述为

式中：D*（t）为驾驶人期望跟车间距；DSV（t）为 t时刻实际跟车距离；kr为虚拟弹簧常数与车辆质量的比值；kv为阻尼系数与车辆质量的比值；vLV（t）与vSV（t）为t时刻LV车和SV车的速度。另外，交通流中的全速度模型［11］也考虑了依赖于车头时距的优化速度及正速度差对驾驶人的影响，该影响（t）为

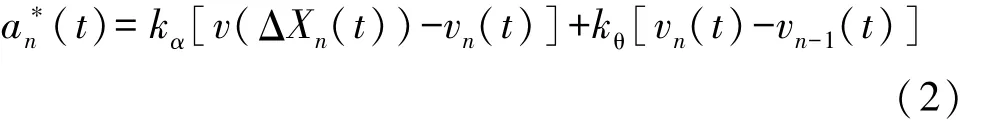
驾驶人期望加速度模型的作用是模拟驾驶人在行车过程中对车辆的控制特性。结合虚拟弹簧理论模型和全速度模型，说明驾驶人的操纵行为与车辆的车头间距和速度直接相关，考虑到车头时距（THW）和避撞时间倒数（TTCi）是反映车距和车速的重要参数，同时能表征驾驶员特性和行车状态，是驾驶人稳定行车时的主要控制目标［12］，故确定期望加速度模型（t）为

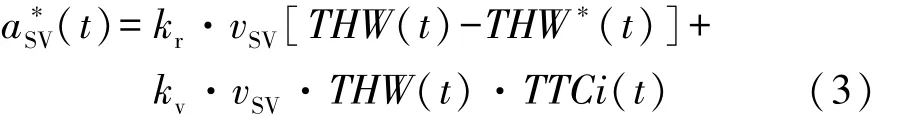
式中：车头时距THW（t）为自车相对前车距离与自车车速的比值；避撞时间的倒数TTCi（t）为相对车速与自车相对前车距离的比值；THW*（t）为期望跟车时距。

换道操作是一个连续的即时行为，主要研究车辆的纵向运动，如车头时距、避撞时间和临界安全距离等［13］。基于此假设，以上模型同样适用于换道过程。但此类模型主要考虑自车与前车之间的防碰撞问题，在换道过程中，除了考虑自车道前车和目标车道前车，还需重点关注目标车道后车的影响。对目标车道后车的跟车时距 THWr和避撞时间倒数TTCir推导为

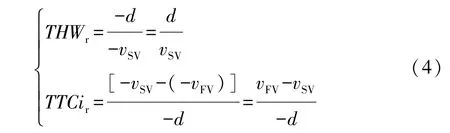
式中d为与前车的相对距离。

本文中综合考虑自车换道时周边多车的状态信息，引用改进的加速度模型进行换道预警。将式（3）两边同时除以自车速度，得预警模型DR（i）为

式中：DR为换道风险指数，表征当前时刻换道风险程度的大小，s-1；i为换道数据的采样序列号（本文中数据采样时间为0.1 s）；THWd，hβ和 hμ为反映驾驶员特性动态变化的参数。

2.2 换道参数的修正

在一个换道周期中，须综合考虑多车道前车及目标车道后车的行驶状态，采用动态权重分配法定量评估各车影响程度大小。引入换道过程中的车辆速度关联度、换道安全系数以及横向偏移作为权重分配的判断指标，对换道参数THW和TTCi进行修正，修正值W（i）和TCi（i）为

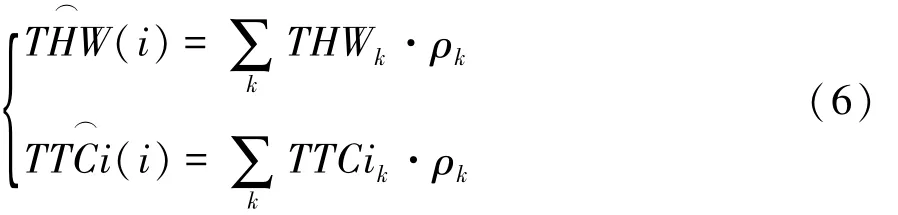
式中：k＝LV，ALV，AFV；ρk为权重系数。对于 ρk的确定，模糊逻辑法能够模仿人脑的不确定性概念判断，是现代人工智能技术的核心［14］，因此可用于驾驶辅助系统中的控制参数调节问题。将3个指标作为模型的输入，权重系数ρk作为输出，建立换道协同车辆的权重调节系统，其结构框图如图3所示。

图3 模块框图设计

（1）速度关联度 即换道车辆与周围车辆相对速度的灰色关联度，描述两车之间的行车稳定程度。基于灰色关联度分析的一般方法分为归一化、求差序列、求两级最大最小差值和求关联系数矩阵4步。关联度系数 gk（i）为

速度关联度的归一值有low，moderate和high 3个等级，分别表示协同车辆与自车的速度关联度较小、居中和较大。

（2）横向偏移 即换道车辆SV与周围车辆的横向位置的差值，是驾驶员对车辆控制量的直接表征参数。以自车与原车道前车为例，自车换道对前车的影响随着横向偏移的增加而逐渐降低。横向偏移 offset（i）为

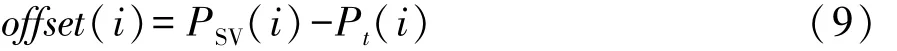
式中：Pt（i）为车辆横向位置，t∈｛LV，AFV，ALV｝。

横向偏移的归一值有near，medium和far 3个等级，对应了周围协同车辆与自车的横向位置的偏差较近、适中和较远。

（3）换道安全系数 即自车与周围车辆的实际距离与安全距离的比值，反映了换道过程中自车与周围车辆纵向距离的安全程度，换道安全系数φs为

式中：do为自车与周围车辆的实际纵向距离；dsafe为两车间的临界安全距离。

对目标车道后车而言，dsafe为换道临界安全距离。换道安全系数的归一值有low，moderate和high 3个等级，对应了换道安全系数较低、中等和较高3个等级。选择常用的高斯函数f作为参数等级的表达形式：

式中σ和c为实数常数。

由此可得到输入和输出的隶属度函数曲线，权重系数的隶属度函数曲线包含VS，S，M，B和VB 5条曲线，分别表示极小、小、中等、大和极大，如图4所示。依据设定的模糊计算规则得到权重系数ρk的等级表达，并采用质心法解模糊得到其定量表达。

2.3 模型参数THW d，hβ和hμ的在线辨识

为实现对驾驶员换道特性的在线学习，采用运算量较小、并能实时处理的递推极大似然估计算法。同时，为降低数据库中过时数据对当前状态判断的影响，引入带遗忘因子的迭代过程，使估计结果更符合当前状态特征［15］。将系统模型考虑为线性差分方程 y（k），其表达式为

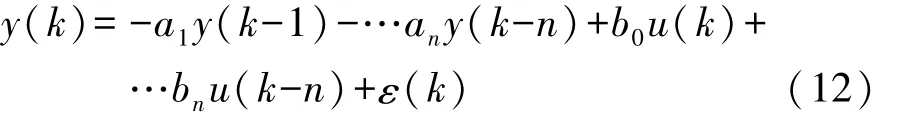
式中：a1，…，an，b0，…，bn为序列系数；ε（k）～N（μ，σ2）为高斯序列；n为序列长度。以上系统模型方程可表示成式（13）所示的向量问题：

式中：Y为观测量，是系统的输出；φ为系统输入量；θ为待估参数变量；e为期望为0的高斯白噪声。

根据式（5）换道预警模型，可得

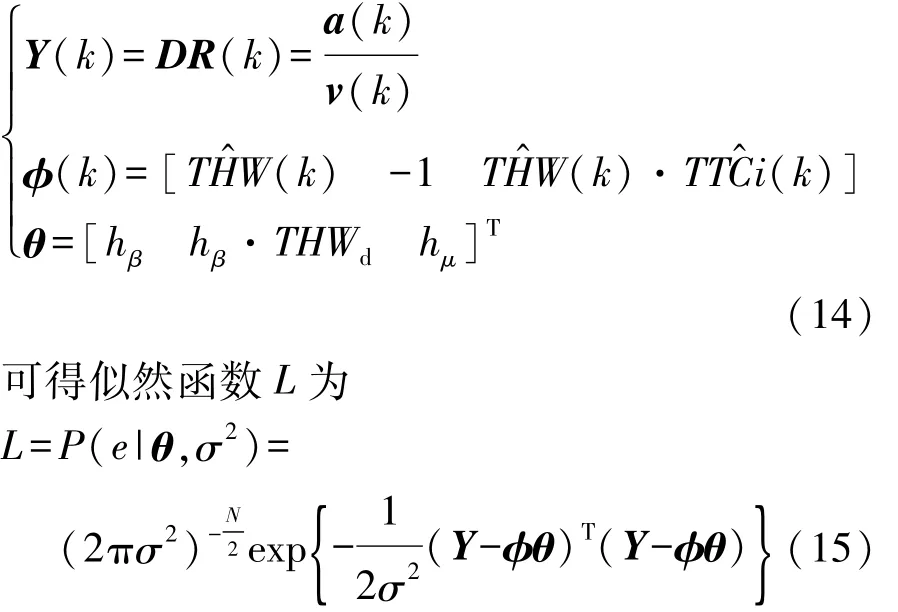
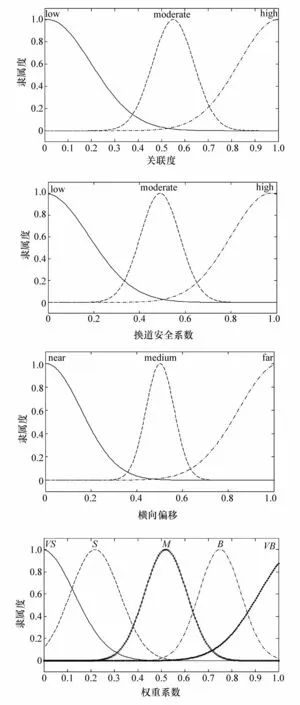
式中σ为序列ε（k）的均方差。

根据极大似然原理，对式（15）中未知参数求偏导，令其为 0，可得待估参数 θ的极大似然估计值：L

根据递推的极大似然估计算法，每观测1次新数据递推计算1次模型参数，如式（17）所示。

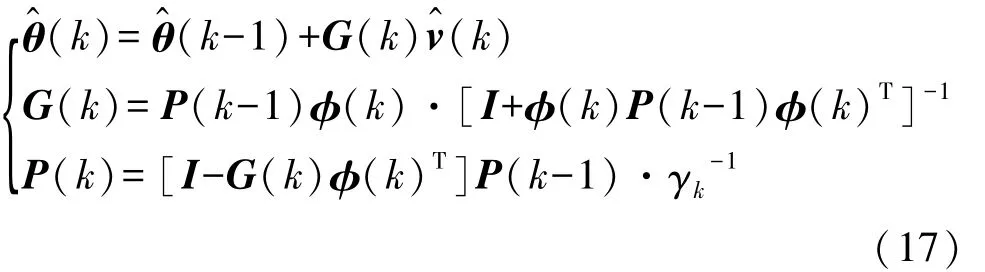
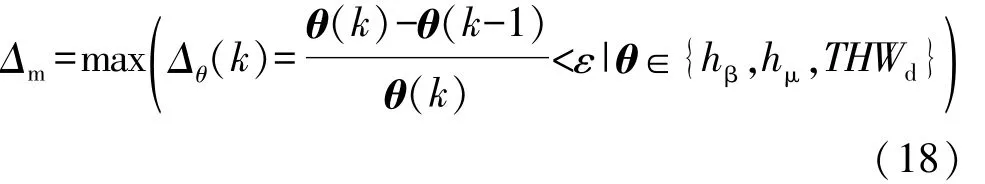
式中ε为适当小的数，即当3个参数的变化波动较小时，递推即可停止。

2.4 换道模型有效性分析

通过分析基于实车试验获取的567组有效换道数据，对本文中建立的换道预警模型的有效性加以验证。基于换道危险评估模型可获得换道过程中的加速度预测值，将车辆加速度预测值与实际值进行对比，如图5所示。

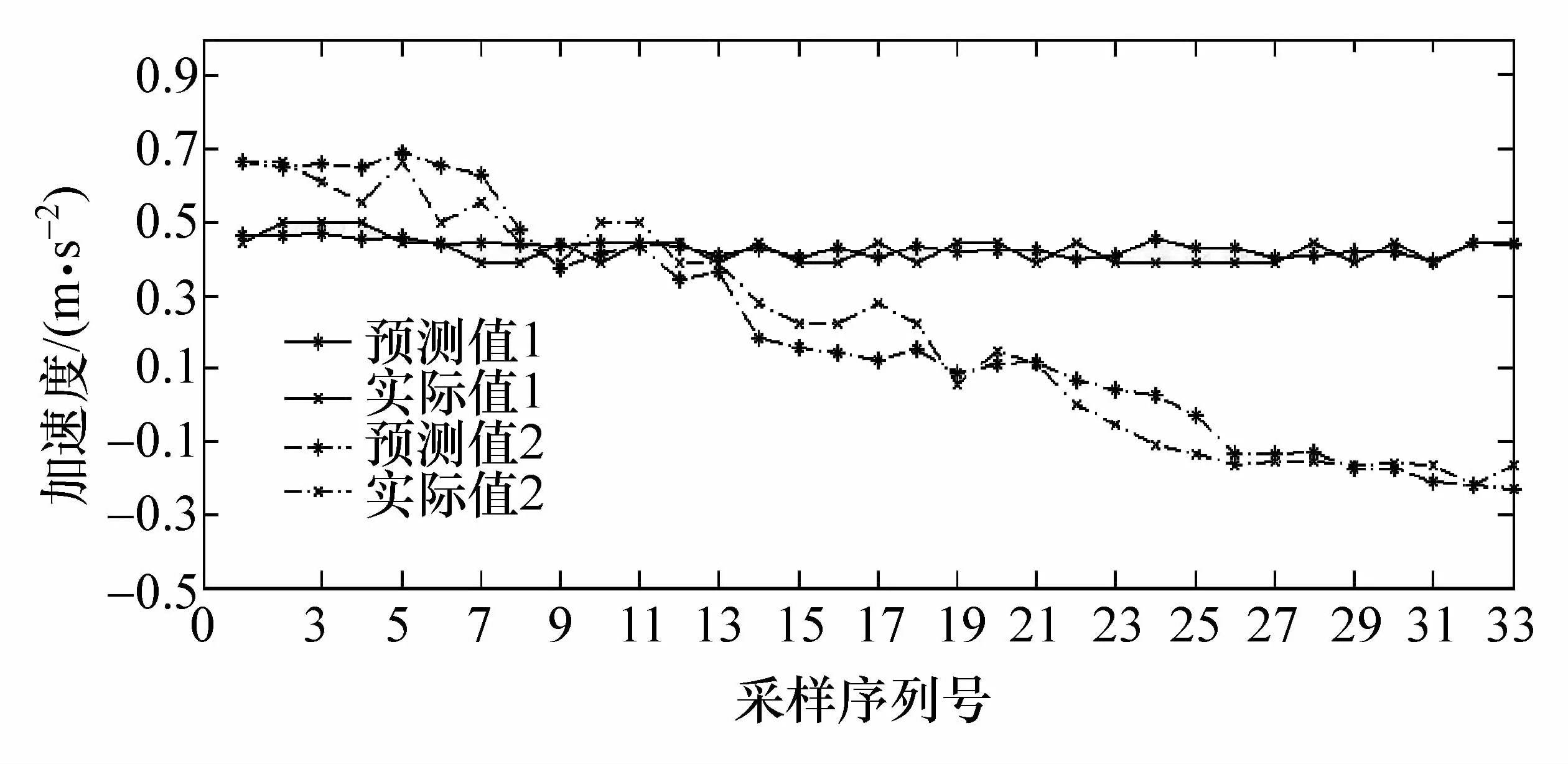
图5 换道过程中的加速度曲线预测

由图5可知，自适应驾驶员特性的加速度预测值符合驾驶员在实际换道过程中的操作特性，表明该模型能够对危险换道情况进行有效预警。

3 预警阈值

3.1 预警阈值的确定

在一次完整的换道数据序列中，通过考察目标车道后车的驾驶行为来判断自车换道过程是否安全。根据文献［16］，高速情况下，车辆危险程度主要受最大制动减速度的影响。后车基本匀速甚至略有加速表明车辆换道行为对目标车道后车的影响小，换道行为安全；相反则说明换道行为不安全。考虑到加速度的取值对驾驶人操作舒适性有较大影响，本文中通过划分最大减速度区间来确定换道过程中后车的危险程度，如表1所示。

表1 目标车道后车危险程度的划分

将各状态下的危险感知值实时存储入数据库，但样本量的不断增加会使得样例类别的混乱程度增大，为获得较为准确的预警阈值，用信息熵的概念来表征判别属性的适应程度。信息熵是描述信息不确定度的期望值，熵越大集合信息的混乱程度越高，反之分类越清晰［17］。信息熵 Entr（X）为

式中：Di＝｛D1，D2，…，Dk｝为特征属性，本文中取 k＝3，分别表示判别结果为安全、较危险和危险；P（Di，X）表示判别结果为Di的分类样例占集合总数X的比例。

将较危险状态的DR值作为区间值属性的条件属性 Ci＝｛C1，C2，…，Cn｝，将数据集按照条件属性Ci的取值进行升序排列得到Ci′，并计算Ci中的最优割点［17］。对选定区间上每一个备选割点P，训练数据集被分割成S1，S2和S3，分割的信息熵定义为数据集 Sj（j＝1，2，3）的类信息熵的加权平均 E（C，P；S），其计算方法为

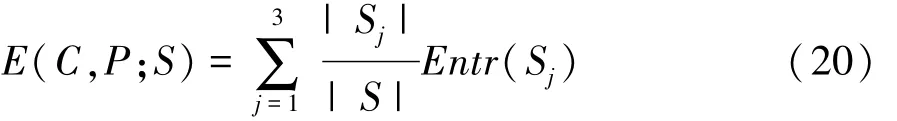
其中 Entr（Sj）由式（20）计算得出。在所有的备选割点中选取使得E（C，P；S）达到最小值的P*，即为特征属性Ci的最优割点，从而得最优阈值DRs为

即当实时危险感知值DR（i）∈DRs时，表明当前处于较危险状态，系统进入一级报警模式；当DR（i）＜DRs，当前为危险状态，系统进入二级报警模式；当DR（i）＞DRs时，为安全状态。

3.2 阈值合理性判断

本文中所建立的预警系统中的信息处理模块选择采用信号检测理论（signal detection theory，SDT）［18］对预警模型进行评价，根据预警系统的判断情况将实时获取的换道数据分成4类，如表2所示。

根据表2分析可知，Ⅰ类和Ⅳ类数据分别表征预警系统的误警情况和漏警情况，即实际情况是正常换道时，系统却发出警报的案例，以及实际情况是危险换道，系统并没有进行预警的案例。若这两种案例占比过大，超出驾驶人对预测模型的容忍限度，说明当前阈值不合理，会降低驾驶人对辅助系统的接受程度。

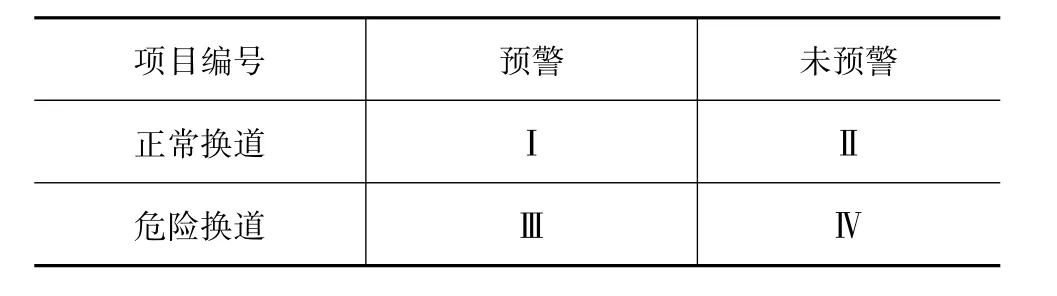
表2 评价结果

3.3 阈值调整规则

数据库中不断添入新数据，同时将过时数据剔除，使算法决策判断的数据样本可靠性提高，也提升了搜索最优阈值的判别能力。当系统漏警和误警情况比率超出限定值时，系统依据现存数据库对最优阈值进行重新搜索，通常将限定值取为8%［12］。

4 算法验证

为验证算法性能，本文中设计了如下实车试验。路线选取为城市快速公路，选择10名驾驶人作为受试对象。试验车辆装配有毫米波雷达、行车记录仪、转向盘传感器、速度传感器、陀螺仪和GPS等设备。车辆信息数据采集系统主要采集车速、转向盘转角、制动和节气门开度等运动参数。工控机负责记录信息数据，将各路信号集中转换，实现数据信号的同步输出，主要试验设备如图6所示。

图6 数据采集试验设备

数据采集方式为设备自动获取数据，后期完成数据的提取处理及样本筛选工作。对获取的换道试验数据进行分类处理，存储各状态的危险感知值，该值由换道预警模型获得，即将实时修正的车头时距、避撞时间的倒数和当前状态下模型最新参数代入计算，部分DR序列如图7所示。

图7 部分DR序列

计算该数据集下的最优割点DRs∈［-0.008，0.057 6］。DR（i）＜-0.008时，换道车辆处于危险状态；DR（i）＞0.0576时，车辆处于安全状态。图8比较了两种状态下自适应模型（ALC）与非自适应模型（N-ALC）的危险感知值序列，自适应预警模型相对于非自适应模型对危险的感知可提前0.3～1 s，为驾驶人采取措施规避危险提供了时间优势。

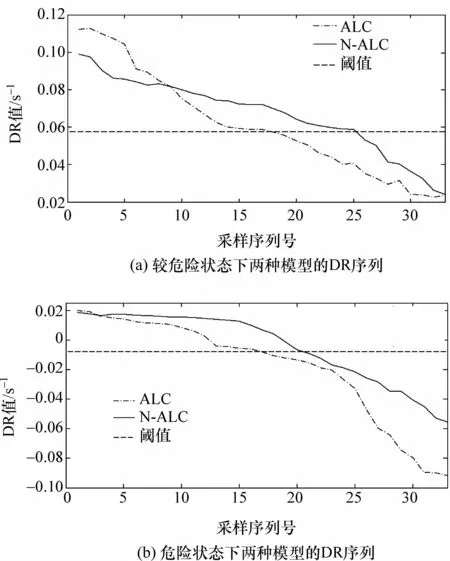
图8 两种模型下的DR序列

利用训练模型对测试数据进行预测，分别将非自适应模型与自适应模型情况下的预测结果与实际结果进行对比，分析系统各状态的识别准确率，具体结果如表3所示。

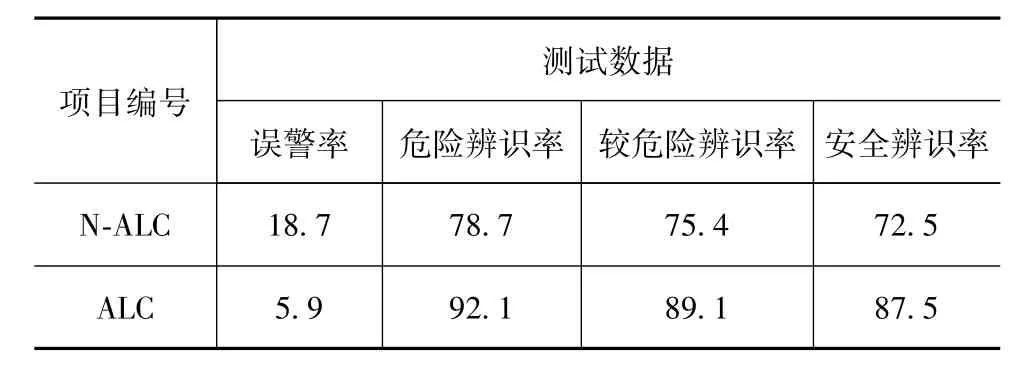
表3 验证结果 %

引入接受者操作特性曲线（receiver operating characteristic curve，ROC）来衡量模型预判的准确率。ROC曲线下的面积AUC（area under curve）值越大分类性能越好。通过计算，分别给出非自适应模型和自适应模型的ROC曲线，如图9（a）和9（b）所示。图9（a）中3种状态的ROC曲线的AUC值分别为t1＝0.818（安全）、t2＝0.836（较危险）和 t3＝0.865（危险）。图9（b）中自适应模型下的 ROC曲线分别为 t1＝0.908（安全），t2＝0.919（较危险）和 t3＝0.941（危险）。由ROC曲线性质可知，AUC越大，其性能就越好。由此说明自适应模型的判别能力较好，且误警率相对于非自适应模型大大降低。

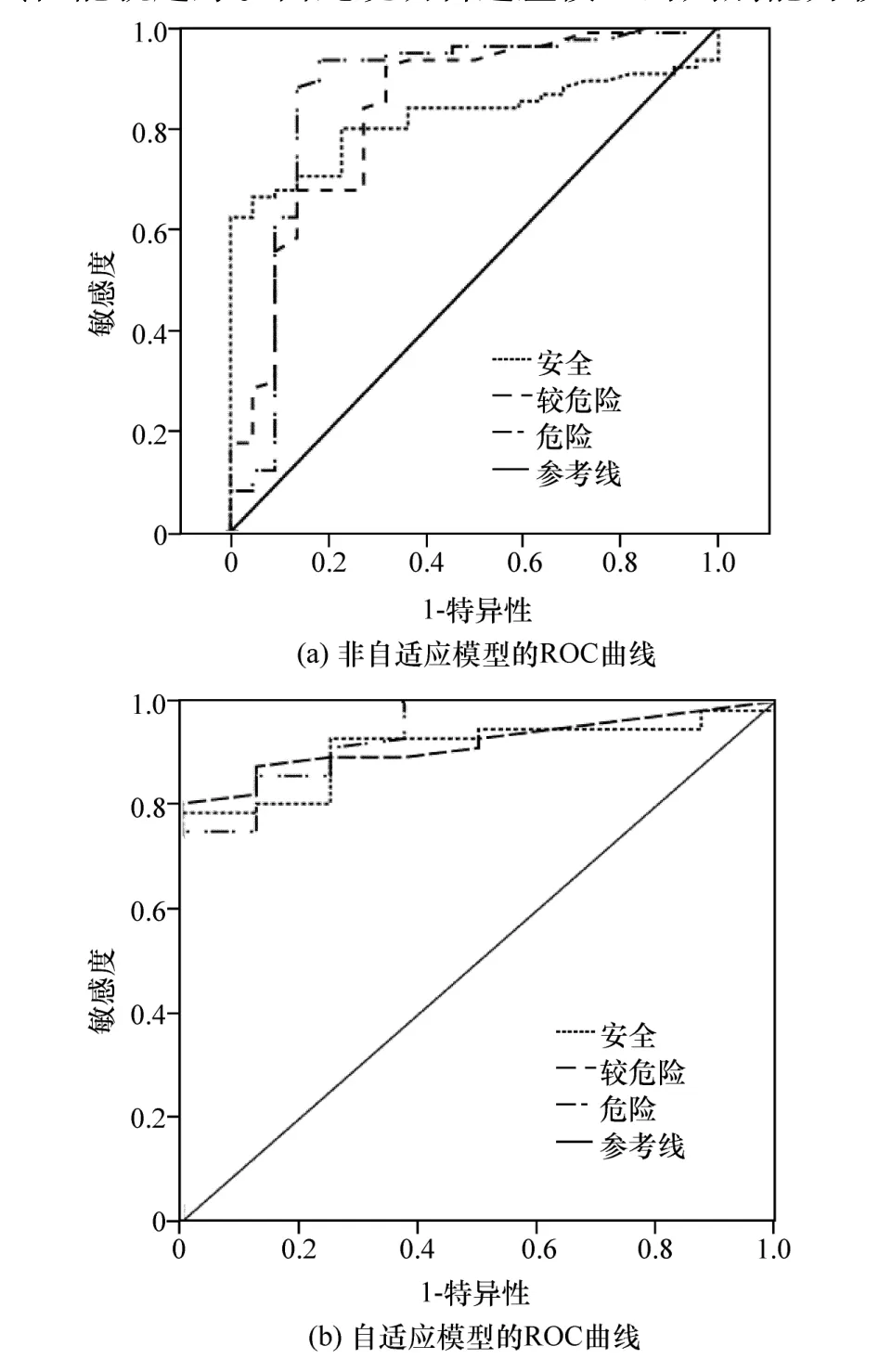
图9 两种模型下的ROC曲线

5 结论

（1）建立了模型参数和预警阈值可调的自适应换道预警模型，并通过实车试验进行了验证。结果表明，参数动态变化的自适应模型更加符合实际的驾驶操作行为，且能够反映不同驾驶员在复杂交通环境下的驾驶风格差异。

（2）自适应预警算法充分考虑驾驶人特性，相对于非自适应模型能较早感知危险，为驾驶人提供0.3～1 s避撞时间。另外，自适应模型的危险状态识别率达到92.1%，误警率低，表明该模型应用于城市快速道路或高速公路上的换道危险感知时有较高的精度，较好地解决了驾驶人与智能辅助系统之间匹配度不高的问题。