基于主成分回归的安徽省城镇居民用电量预测模型

潘玉荣，贾朝勇

（蚌埠学院理学院，安徽蚌埠233000）

居民生活用电量是全社会用电量的一个重要组成部分。近些年来，随着安徽国民经济的快速发展和居民生活水平的不断提高，居民生活用电总量也在不断增加。2017年城乡居民生活用电总量达到3 210 585万千瓦时，占安徽省全社会用电总量的16.7%。而且，未来几年安徽省居民生活用电量仍保持着较大的增幅［1］。分析城镇居民生活用电量增加的动因，准确预测居民生活用电量将为电力系统规划和运行提供一些决策信息。很多学者对居民用电量的影响因素展开了研究［2-4］。文献［5-7］利用多元回归分析方法，建立了居民生活用电量与影响因素间的回归模型。然而当影响因素间存在严重的多重共线性，多元回归建立的模型就失去了统计意义，所以引入新的方法对居民用电量进行分析和预测是十分必要的。文献［8］基于主成分－BP神经网络法对我国农村居民用电量进行了预测研究。文献［9］根据2007-2013年淮安市居民生活用电量数据，利用灰色预测模型对淮安市居民生活用电消费进行分析及预测。本文则以安徽省城镇居民生活用电量相关数据为例，详细分析了城镇居民生活用电量的影响因素，并应用主成分回归法建立城镇居民用电量的预测模型。

1 安徽省城镇居民生活用电的影响因素分析

安徽省城镇居民生活用电量与很多因素有关，本文从安徽省统计局网站收集到2005-2016年城镇居民生活用电量相关数据并进行了整理，利用EXCEL软件对该数据进行了基本分析。

1.1 经济社会因素对城镇居民生活用电的影响

近十几年来，随着安徽经济的快速发展，居民收入大幅度提高。统计数据显示，城镇居民的年人均可支配收入从2005年的8 470.68元提高到2016年的29 155.98元，提高了约3.4倍。居民可支配收入的提高带动居民生活用电量的增加。由图1可知，城镇居民人均收入的增长与城镇居民生活用电量的增加具有同向性。

随着我国城镇化进程的推动，安徽省常住人口从2005年的6 120万人增加到2016年的6 196万人，城镇化率由35.5%上升到51.99%，城镇常住人口数的增加使城镇居民生活用电总量快速增长。其次，安徽房地产市场的快速发展使城镇居民的居住条件得到极大改善，城镇居民的人均住房建筑面积大幅增加。2005年安徽人均住房建筑面积仅19.9 m2，到2016年增加到36.9 m2，几乎翻了一倍，人均住房建筑面积与居民生活用电量相关性很强。在住房面积改善的同时，人们会购买更多的大功率家用电器如空调、冰箱、洗衣机等，而大功率家用电器的使用是居民生活用电量快速增长的原因之一。此外，电价是居民用电量的一个影响因素，特别是我国实现阶梯电价以来，电价在一定程度上对城镇居民用电量起到制约的作用。然而，由于我国现行的电价交叉补贴政策，居民电价仍处于较低水平，电价对居民用电量的总体影响相对较小。

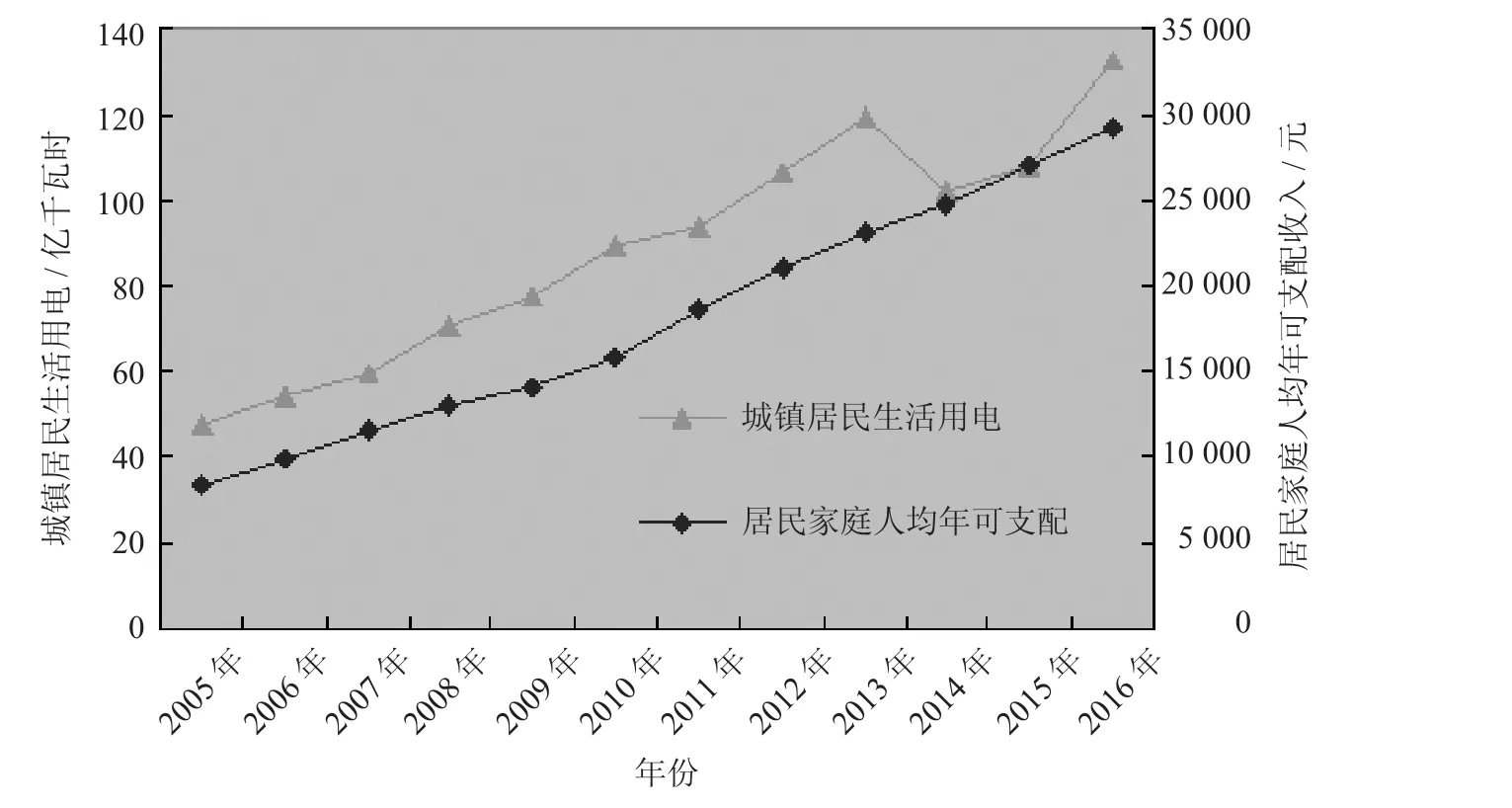
图1 城镇居民生活用电与城镇居民人均年可支配收入序列图

1.2 自然因素对城镇居民生活用电的影响

安徽省属于温和气候型气候，四季分明，雨水充沛，年平均气温在14～17℃左右，是典型的夏热冬冷地区。夏季气温的高峰和冬季气温的低谷都导致了空调和采暖用电的高峰。图2给出安徽省2015年1月到2016年12月居民月用电量与月平均气温的关系图。从图2中可以看出，夏季月耗电量的波峰与月平均气温的波峰几乎同时出现，而冬季月耗电量的波峰与月平均气温的波谷几乎同时出现。因此，气温对夏季和冬季居民用电的影响不容忽略，气温对安徽省居民的月用电量存在显著影响。

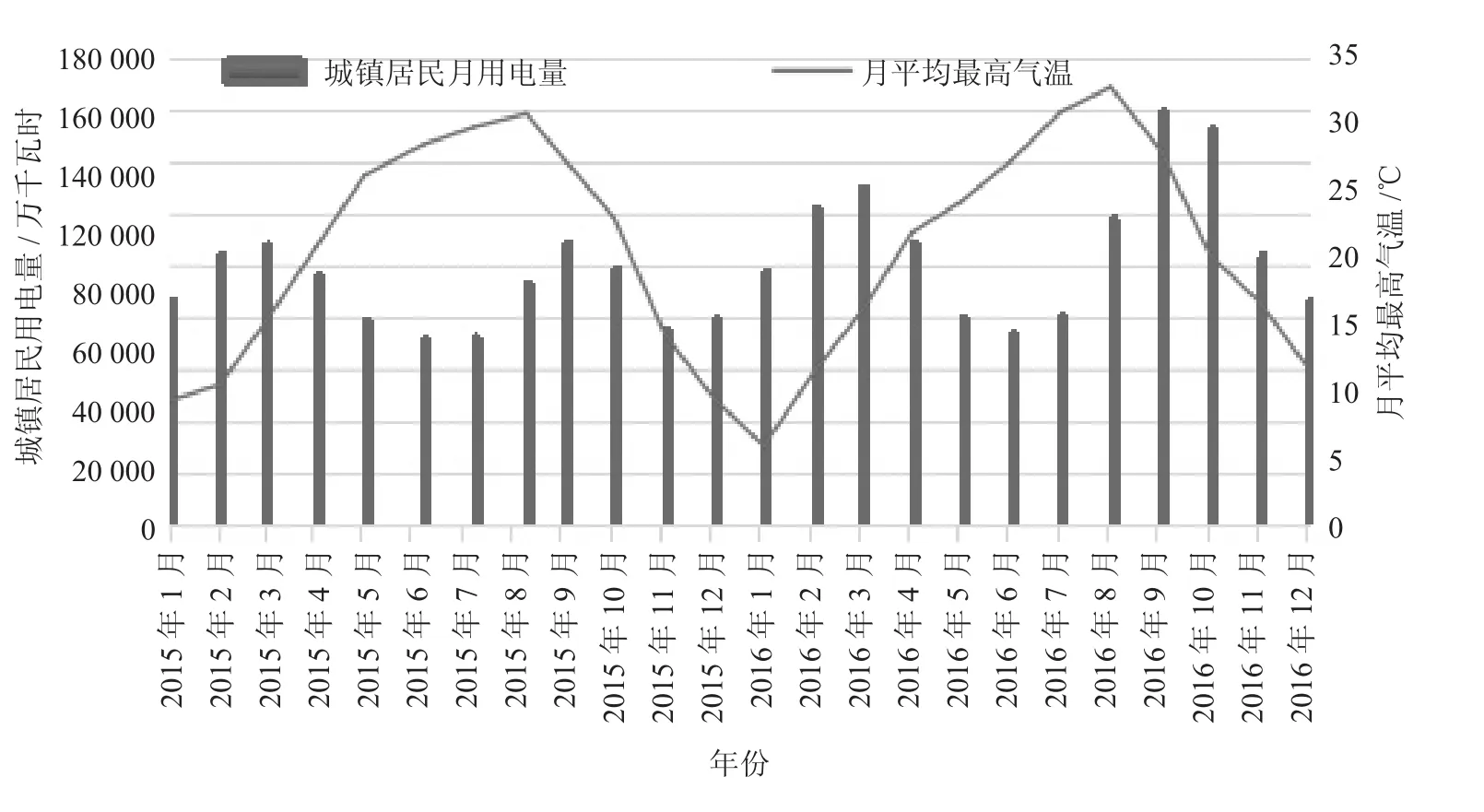
图2 城镇居民月用电量与月平均气温关系图

2 安徽省城镇居民生活用电量的预测模型

2.1 变量的选取及多重共线性问题

影响安徽省城镇居民生活用电的影响因素很多，根据上述基本分析，本文选取了城镇居民人均年可支配收入x1（元）、城镇居民人均建筑面积x2（m2）、城镇居民家庭年平均每百户空调拥有量x3（台）、x4城镇常住人口（万）、年平均气温x5（℃）作为城镇居民年生活用电总量y（亿千瓦时）主要影响因素。应用SPSS软件，对城镇居民生活用电量与各因素进行描述统计分析和相关分析，得到表1和表2。从表2可看到，y 与 x1、x2、x3、x4的相关系数分别为 0.956、0.936、0.954、0.95，相关系数接近于 1，说明城镇居民年生活用电量与这四个变量存在较强的正相关关系。而年平均气温与城镇居民年生活用电量相关系数仅为-0.218，呈负的线性相关关系且相关性较弱，这说明虽然气温对夏季和冬季居民家庭用电影响不容忽略，然而平均到全年以后影响却不显著。因此，下面的分析中剔除了年平均气温这个变量。

表1 描述统计量

表2 城镇居民年生活用电量与各影响因素的相关性

因y与x1、x2、x3、x4存在显著的线性相关关系，现以y为被解释变量，城镇居民人均年可支配收入、城镇居民人均建筑面积、城镇居民家庭年平均每百户空调拥有量与城镇常住人口作为解释变量，进行多元线性回归，得到表3。

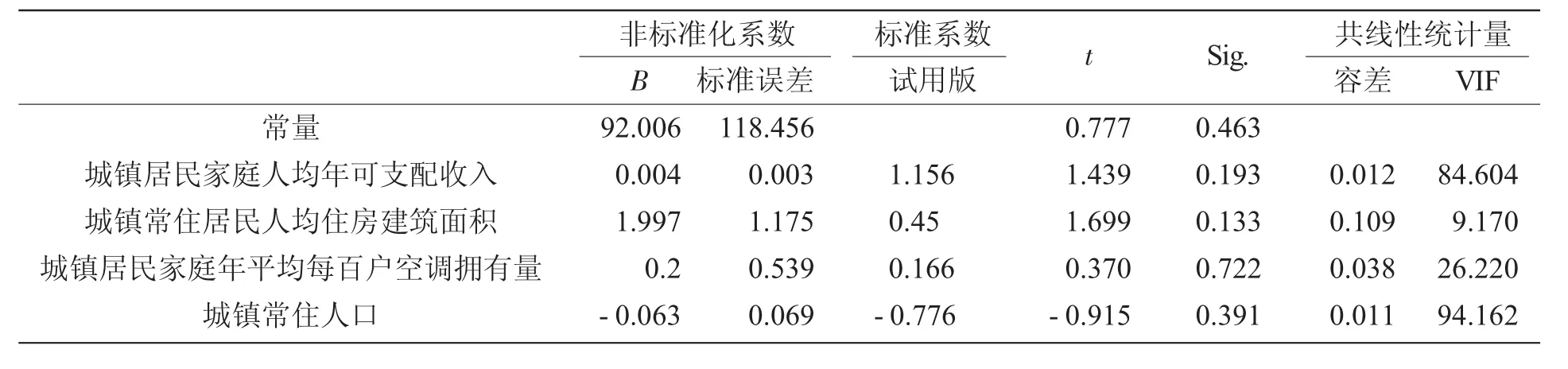
表3 多元回归结果和共线性统计量

从表3的第6列数值可看到，若取显著水平α=0.05，4个解释变量的回归系数显著性t检验的概率P均大于显著水平α，说明该模型的回归系数均未通过显著性检验，所以回归模型不可用，需重新建模。表3的最后两列分别是解释变量的容忍度（Tolerance）和方差膨胀因子VIF，4个回归系数对应的容忍度分别为0.012、0.109、0.038、0.011，其中有3个接近于0，说明解释变量间存在多重共线性，再从VIF的值看，有3个远远大于10，这说明解释变量间确实存在严重的多重共线性。

2.2 主成分回归模型的建立

主成分回归是回归分析中解决多重共线性问题非常有效的方法，主成分回归建模的详细过程参见文献［10］。接下来，对 y、x1、x2、x3、x4进行主成分回归分析。

2.2.1 数据的标准化及KMO检验

为了分析结果不受原始数据的量纲影响，对y、x1、x2、x3、x4观测数据进行标准化，标准化后的变量分别命名为 zy、zx1、zx2、zx3、zx4。接着检验变量 zx1、zx2、zx3、zx4是否适合作主成分提取，得到表4。

KMO检验统计量是用于测度变量间简单相关系数和偏相关系数的指标，它的取值范围为0～1，KMO的值越接近1，意味着变量间的相关性越强。从表4可知，KMO的观测值为0.801，说明原有变量相关性较强。另外，再根据Bartlett的球形度检验统计量的观测值为84.335，相应的概率P是0，如果取显著水平α=0.05，则P＜α，应拒绝原假设，说明相关系数矩阵与单位阵有显著差异，即变量间存在相关性。因此，zx1、zx2、zx3、zx4适合作主成分提取。

表4 KMO和Bartlett的检验

2.2.2 主成分提取

利用SPSS软件对4个变量进行主成分提取，得到表5。从表5中可看到，第一个特征值是3.885，能解释原有4变量总方差的96.386%，累计方差贡献率达96.386%，大于85%。因此，我们只要提取第一主成分就够了。

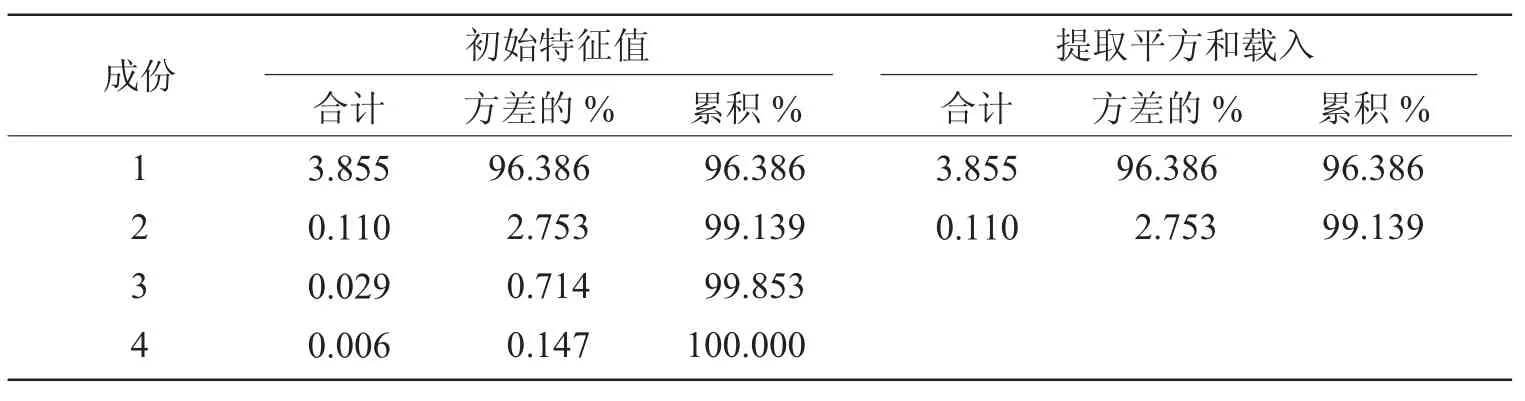
表5 主成分提取汇总表

第一个特征值为λ1=3.855，则对应的标准正交化特征向量［10］是

所以，可以写出主成分系数矩阵（见表6）。再根据特征向量可求得主成分得分函数F1为

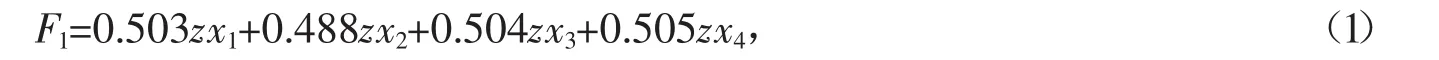
将 zx1、zx2、zx3、zx4的观测值代入式（1），即可得到变量 F1的值。

表6 主成分矩阵

2.2.3 线性回归

用安徽省城镇居民年生活用电量的标准化值zy，对主成分F1进行线性回归得表7。由表7可写出回归方程为

根据回归结果可知，回归方程（2）的多重可决系数R2为0.934，接近于1，说明方程的拟合度较好。如果取显著水平α=0.05，方程（2）对应的统计量F的值为142.42，相伴概率为0，0＜α，说明该回归方程是显著的。另外，F1前的回归系数为0.492，相应的概率为0，而0＜α，说明该回归系数均通过了显著性检验。

再将式（1）代入式（2）中，得

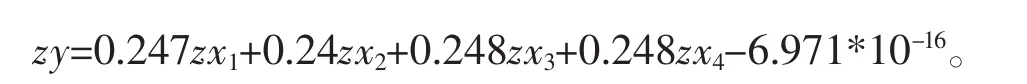
表7 线性回归结果

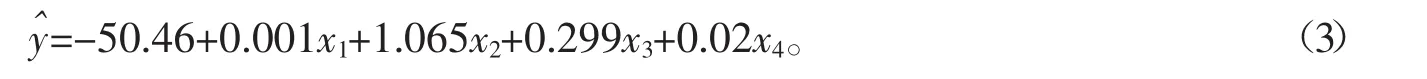
从经济意义角度看，该模型与实际情况相吻合。在其他因素不变情况下，人均收入每增加1 000元，城镇居民年生活用电量增加1亿千瓦时。同样在其他因素不变情况下，城镇居民人均建筑面积每增加1 m2，相应的城镇居民年生活用电量增加1.065亿千瓦时，这说明城镇居民居住面积的增加对居民生活用电总量影响较大。

3 模型的预测

现用估计模型对安徽省城镇居民生活用电量进行预测，并将预测结果和实际值进行了比较，得到图3。从图3可以清楚地看到，2012年以前城镇居民年生活用电量预测值和实际值较接近，而2013年、2014年，两者存在一定差异。另外，我们还计算了预测值和实际值的绝对误差值和相对误差值，相对误差最小的年份是2011年，仅为-0.005，相对误差最大的年份是2013年，为0.11。总体而言，该主成分回归模型的预测效果较理想。

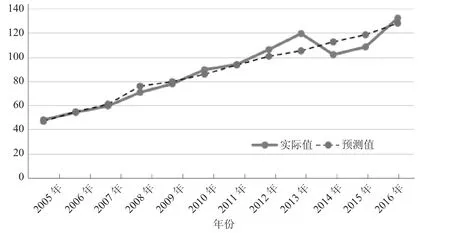
图3 城镇居民年生活用电量预测值与实际值比较

4 结论

为研究影响安徽省城镇居民生活用电量的主要影响因素，本文从安徽统计局网站收集了2005-2016年的城镇居民生活用电相关数据，详细分析了各因素与城镇居民用电量的关系，并应用主成分回归法建立城镇居民生活年用电量与主要因素之间的预测模型。分析表明：城镇居民居住条件改善是安徽居民生活用电增长的主要原因，其次，家用大功率电器增加、城镇居民可支配收入的提高以及城镇常住人口的增长对城镇居民生活用电量的增长起到重要的促进作用，而其他因素对安徽省城镇居民用电量的影响不显著。