非线性网络控制系统故障检测和控制器协同设计
陆诗敏,金朝永 *,罗俊玉
(广东工业大学应用数学学院,广东广州510520)
伴随着科学技术和工业生产的进步,网络控制系统的研究得到迅速发展,与传统的点对点式控制系统相比,网络控制系统具有信息资源共享、远程操作和灵活性强等优点,在工业实践中得到广泛应用,如过程控制系统、远程医疗、建筑自动化、高速列车控制、航空及航天、电机自动控制、机器人系统等领域[1-4],但同时也带来新的问题和挑战,比如网络传输带宽的有限性、数据丢包、网络诱发的传输时滞、数据错序、误码等,导致系统性能下降甚至不稳定,而由于对动态系统的更高性能、更高安全性和可靠性标准的需求不断增长,越来越多学者开始在控制领域中研究故障检测与隔离技术问题[5-7]。
文献[8-9]将两个通道的数据丢包建模成相互独立的伯努利白噪声序列,研究离散网络系统的基于观测器的故障检测问题。文献[10-11]研究一类带有时滞的离散网络控制系统,协同设计故障检测滤波器和控制器。上述文献只研究了故障检测滤波器的设计,这是一种开环设计问题。然而,在实际的网络控制系统中,由于控制元件受环境或本身物理特性的影响,控制器参数的微小摄动都有可能导致系统不稳定,这就要求把控制器的影响考虑进去,协同设计故障检测滤波器和控制器是不可缺少的。另一方面,现有的大多数文献都是关于线性网络控制系统,而带有一些约束条件且非线性网络控制系统的故障检测方法却很少,常用方法有:1)采用T-S模糊模型将非线性系统通过一系列局部线性系统逼近[12];2)利用鲁棒H∞控制理论将非线性问题转化为带有约束的线性不等式优化问题。
本文针对一类具有扇区非线性的网络控制系统,协同设计故障检测滤波器和控制器。通过将基于观测器的故障检测滤波器作为残差生成器,基于李雅普诺夫方法,给出并证明误差系统均方指数稳定且具有H∞性能的充分条件。将网络系统的控制器和故障检测滤波器的参数求解转化为线性矩阵不等式的凸优化问题,以确保残差和故障估计误差尽可能小。
1 问题描述
考虑如下一类扇区非线性的离散网络控制系统
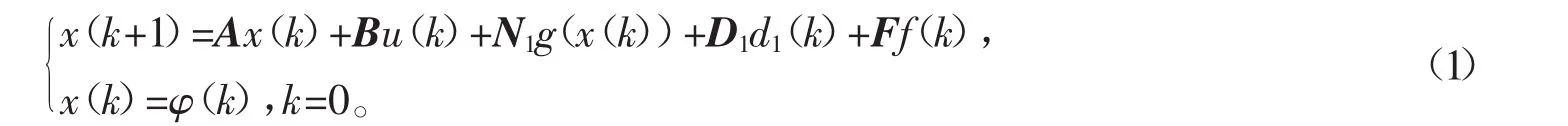
其中,x(k)∈Rn为状态向量;u(k)∈Rm为控制输入向量;d1(k)∈l2[0,∞)为扰动输入;f(k)∈Rl为待检测的故障;φ(k)为给定的初始条件;g(x(k))为关于状态变量的非线性函数;A,B,N1,D1,F为具有适当维数的常数矩阵;非线性向量函数g(·)满足初始条件g(0)=0且满足扇区有界条件

其中,S1,S2∈Rn×n是已知实数常值矩阵,S=S1-S2是对称正定矩阵。
注1 式(2)给出的扇形非线性是文献[7]研究的Lipschitz非线性的一般形式。
网络系统中测量随机丢包的过程可描述为

其中,y(k)∈RP为测量输出向量;d2(k)∈l2[0,∞)为测量噪声;C和D2为具有适当维数的常数矩阵;α(k)为传感器到控制器通道上的随机丢包情况,当α(k)=1时,无数据丢失,当α(k)=0时,数据全部丢失,随机变量α(k)∈R为满足Bernoulli 0-1序列分布的白噪声系列,有
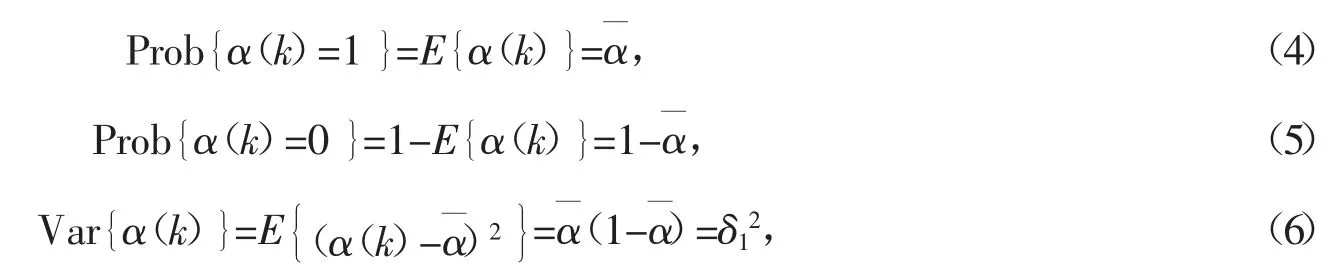
对于离散网络控制系统设计如下基于观测器的故障滤波器
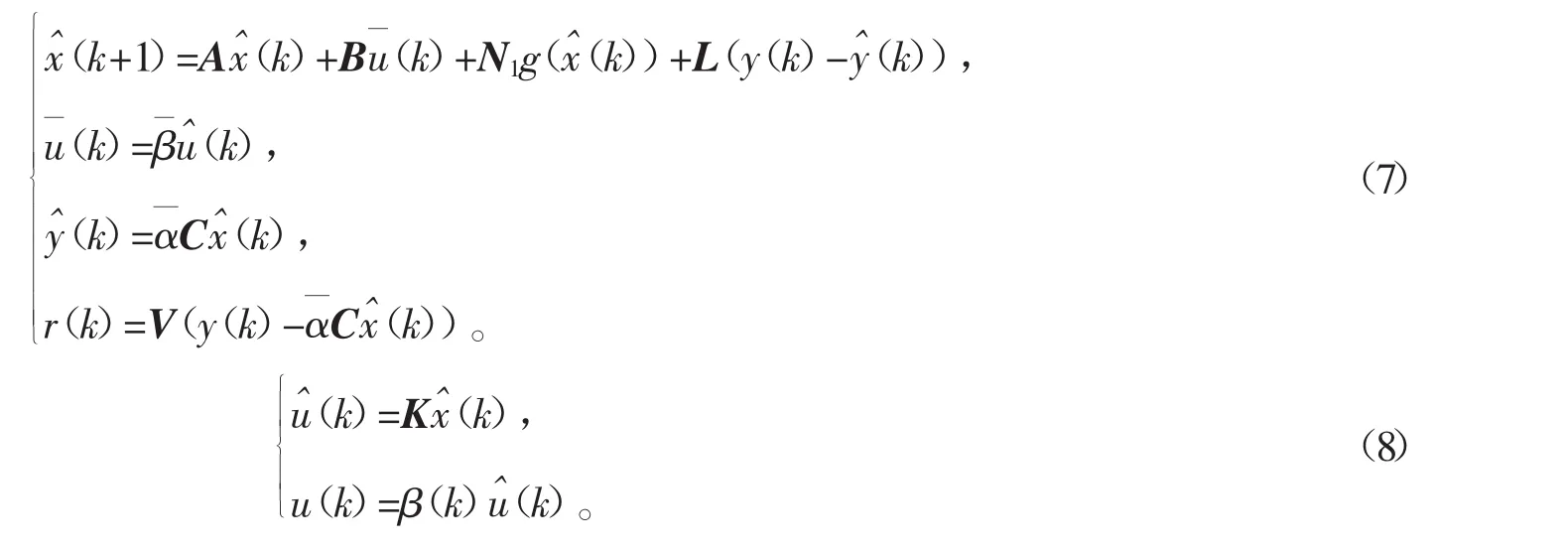

定义如下的状态估计误差和残差误差信号

将式(1)、(3)、(7)、(8)代入式(12),得闭环控制系统的表达式为

其中
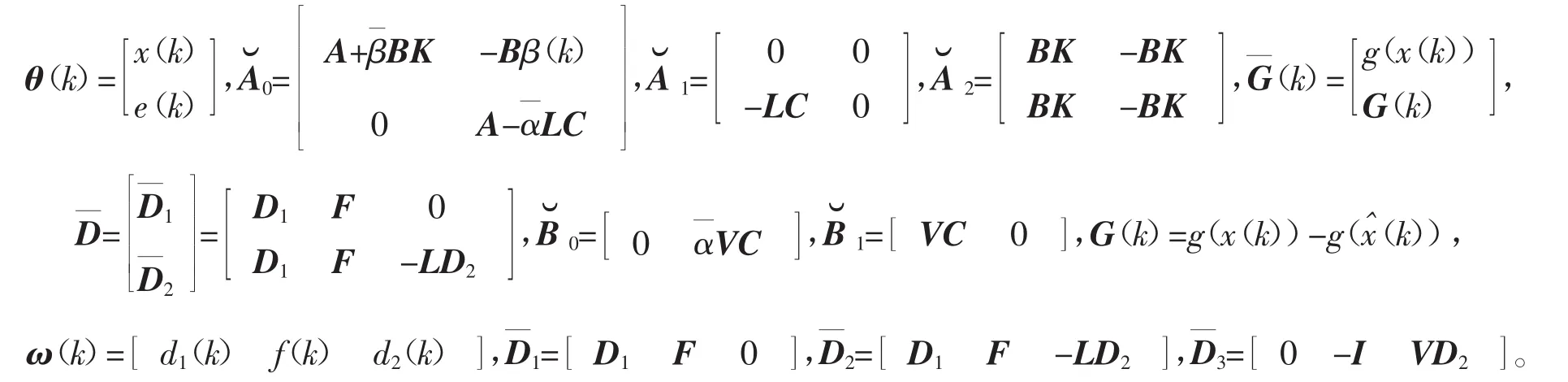
为推导出主要结论,引入如下定义和引理:
定义 1 对于系统(13),当 ω(k)=0时,存在 ρ>0和 τ∈(0,1)使得

则称系统为均方意义下指数稳定。
本文通过以下规则来判断系统是否有故障

引理 1[14]假设 g(·)是一个向量值非线性函数,S1,S2∈Rn×n是已知实数常值矩阵,若

则
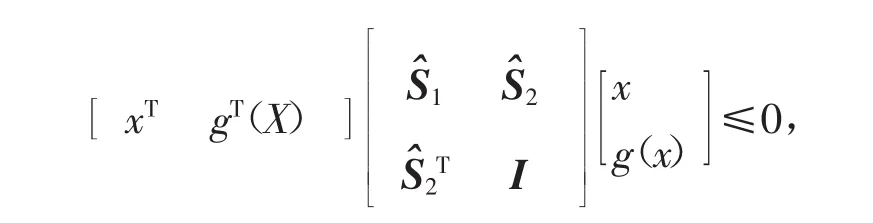

2 故障检测滤波器和控制器协同设计
2.1 H∞性能分析

证明 定义如下形式的Lyapunov函数
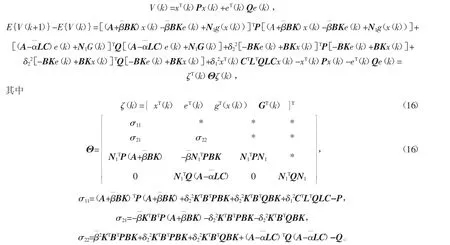
由式(2)及引理1得

根据引理2,如果存在正定对称矩阵P>0和Q>0,存在非负的标量τ1,τ2,使得

由于式(19)中同时存在 P,P-1,Q,Q-1,因此式(18)不是线性矩阵不等式。定义
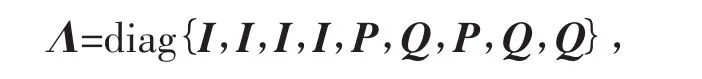
对式(19)分别左乘矩阵ΛT和右乘矩阵Λ,得到线性矩阵不等式(14),则

因此当w(k)=0时,系统(13)是均方指数稳定的。
现在分析闭环网络控制系统的H∞性能指标。
当 w(k)≠0时,有


由式(2)及引理1得

根据引理2,如果存在正定对称矩阵P>0和Q>0,存在非负的标量τ1,τ2,使得

由于式(23)中同时存在 P,P-1,Q,Q-1,因此式(22)不是线性矩阵不等式。定义
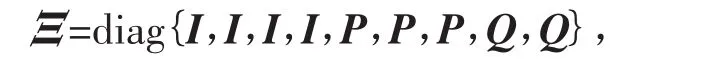
对式(23)分别左乘矩阵ΞT和右乘矩阵Ξ,得到线性矩阵不等式(15),则
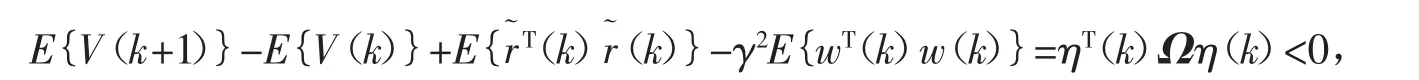
从0到∞累加后,即可得到
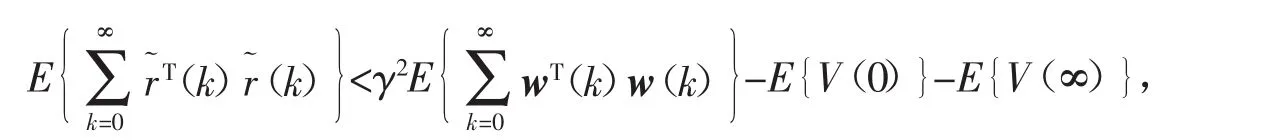
由闭环系统(13)是均方指数稳定的及θ(0)=0时,可得到

这说明系统(13)具有H∞性能指标。
假设 1[16]B 是满列秩矩阵,rank(B)=m 存在两个正交矩阵 U∈Rn×n和 W∈Rn×n,使得

其中,U1∈Rm×n,U2∈R(n-m)×n和Σ=diag{σ1,σ2,…,σm},σi(i=1,2,…,m)是B的非零奇异值。
引理3 B∈Rn×m是满列秩矩阵,如果矩阵P满足

其中,P11∈Rm×n>0,P22∈R(n-m)×(n-m)>0。U1,U2与假设 1 的 U1,U2相同,则存在一个非奇异矩阵 P1∈Rm×n,s.t.BP1=PB。

则闭环网络控制系统(14)是均方指数稳定的,且当w(k)≠0时,系统(14)具有H∞性能指标。
注2在闭环网络控制系统(14)满足性能指标下,建立如下最优化问题

3 实例仿真
在本节中,将给出一个数值例子来验证故障检测与控制器协同设计方法的有效性。

假设网络控制系统的初始状态为 x(0)=[0 0]T,采样周期 T=1 s。

图1 闭环系统的状态
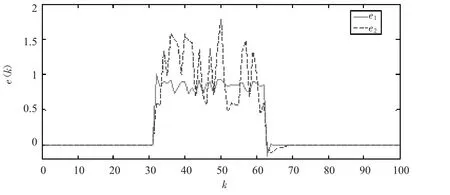
图2 状态估计误差

图3 残差信号

图4 残差评价函数
4 结论
本文针对一类扇区非线性的离散网络控制系统,协同设计了基于观测器的故障检测滤波器和控制器参数,在实际应用过程中考虑了控制器的影响,并证明了该系统均方指数稳定,且达到鲁棒干扰抑制水平。仿真算例说明了在有外部干扰的情况下,设计的鲁棒故障检测滤波器具有优异的性能。

