基于时频图蚁群边缘检测的FSK信号识别
郑文秀, 马 昊
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
随着无线通信中信号的调制方式越来越丰富,在通信电子对抗、电子侦察和无线电信号管理等领域识别并区分接收信号的调制类型越来越重要。只有正确地识别并区分接收信号,才能进行后续的信号分析和处理。
目前,针对频移键控(frequency-shift key, FSK)信号调制的识别方法,如基于瞬时特征分析的方法[1-2]、基于小波变化方法[3-4],需要将精确载波频率、初始相位作为先验知识。日益复杂的通信环境,使得先验知识难以应用于未知情况,这给信号调制方式识别带来很大困难[5]。文献[6]提出了低信噪比条件下的FSK信号调制特征提取方法,提高了调制特征识别的准确性,但未能解决时频分析中的频率混叠问题。基于时频图增强的FSK信号特征提取,降低了的噪声影响,但会忽略微弱信号的频率特性[7]。文献[8-10]提出基于信号星座图形状和最大似然准则的方法,在实际中,基于模糊C-均值(fuzzy c-means,FCM)聚类方法的星座图恢复算法[11]无法预先得到需给定的聚类数目,在低信噪比条件下,其基于最大似然准则分类判别算法的准确度明显降低[12]。
为了识别FSK信号的调频方式,进而对其有效分类,本文拟提出一种基于时频图蚁群边缘检测的算法。该算法运用离散短时傅里叶变换(discrete short time Fourier transform,DSTFT)处理图像,将时频图转换成时频二维灰度图并做增强处理,结合基于蚁群的边缘检测算法检测增强处理的时频二维灰度图边缘[13-14],由边缘检测图的投影确定FSK信号的谱线数,并区分FSK信号载波数量。
1 FSK信号原理及其特征识别
二进制频移键控2FSK信号,载波频率随着调制信号“0”和“1”的变化呈现周期性变化,“0”对应载波频率f1,“1”对应载波频率f2。
FSK信号s(t)的时域表达式[15]为
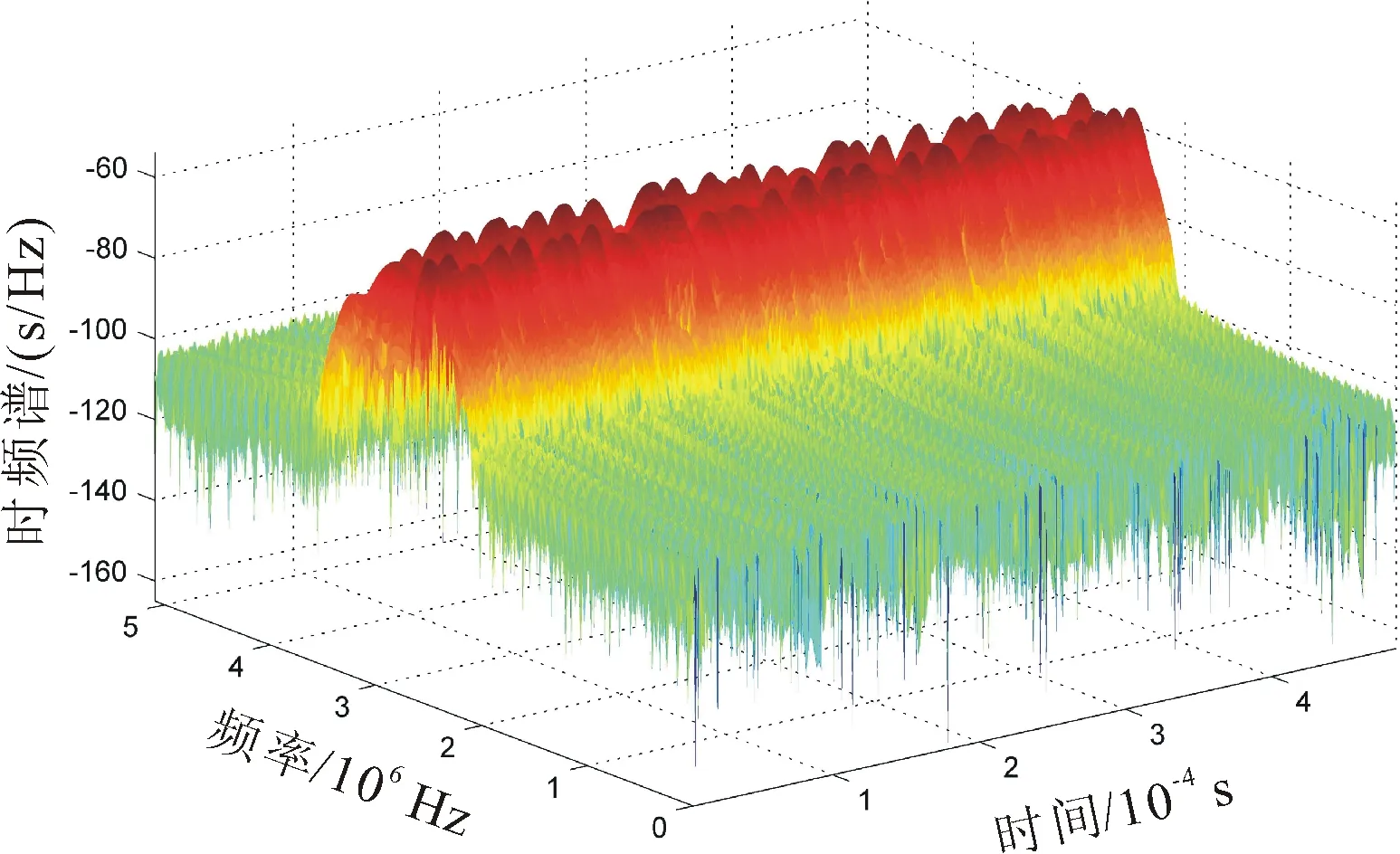
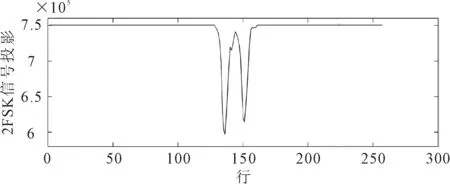
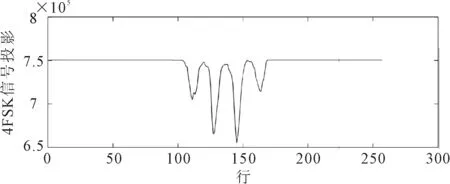
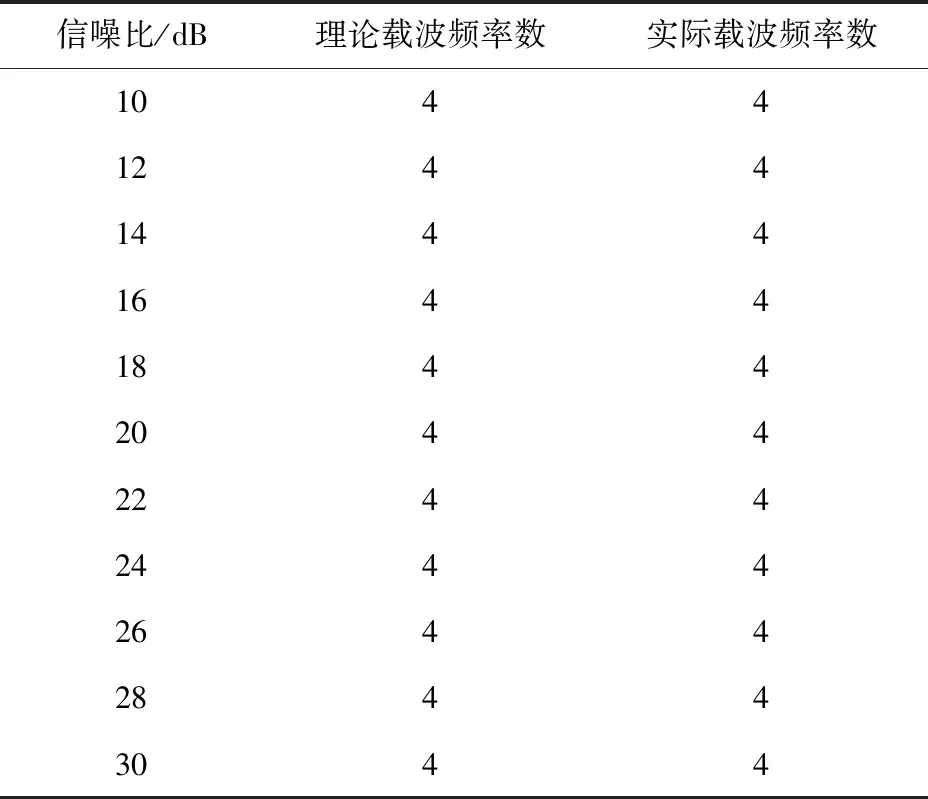
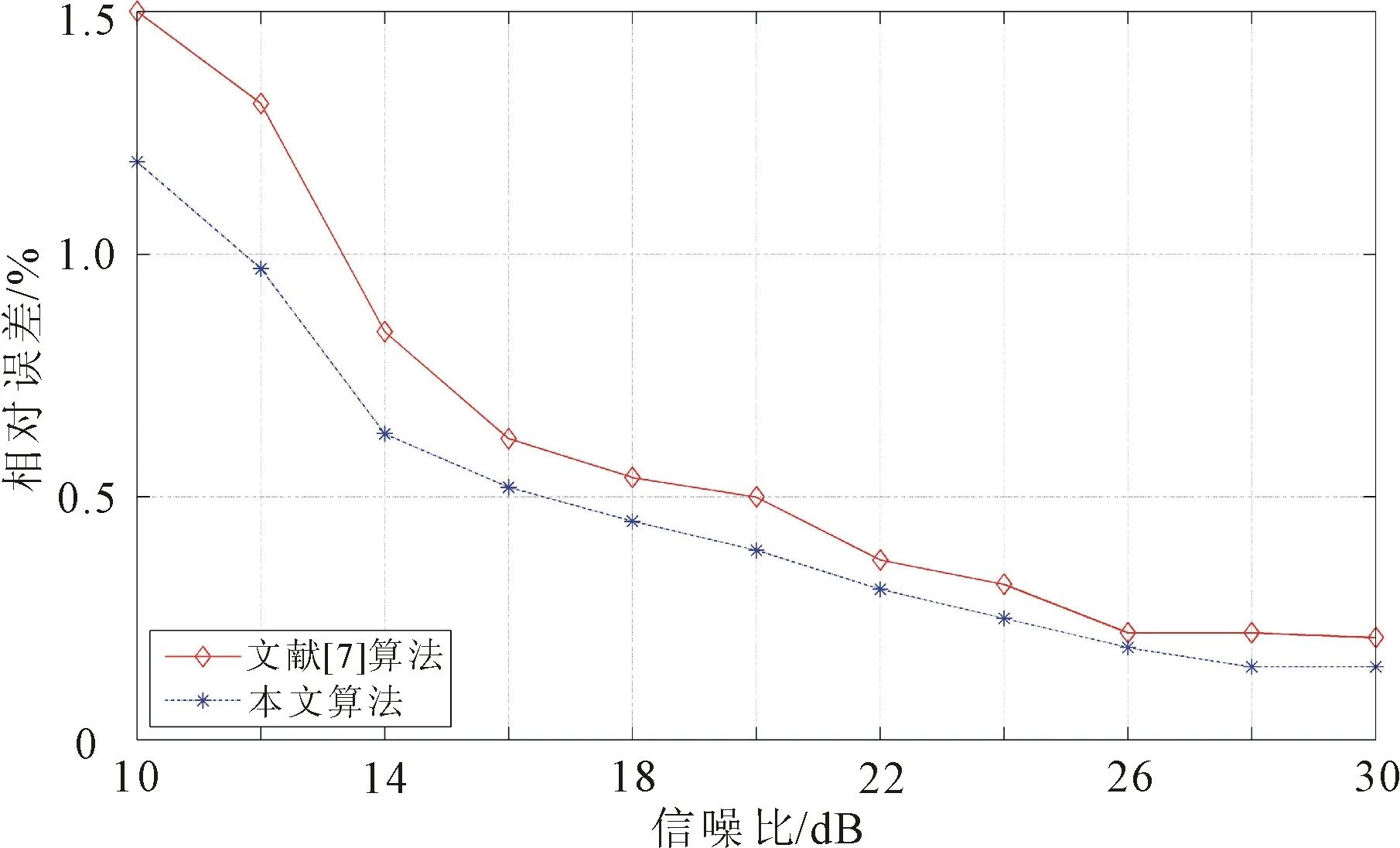
s(t)=Acos[2πf(t)+φ(t)] (0≤t (1) 其中,A为信号幅度,φ(t)为瞬时相位,T为键控信号周期,f(t)为键控信号频率。 键控信号f(t)的瞬时频率[15]为 (2) 其中,f0为中心频率,Δf为频率偏量。fh和fl分别为上、下边频率。FSK信号由两个边频率为fh和fl的正弦信号组成。 FSK信号具有周期性,当傅里叶级数展开时,瞬时相位θ(t)具有连续性,令其为0,则有[15] (3) (4) 其中,f为键控信号频率,m和n分别代表移频指数和中心载频所对应的谱线位置。 FSK信号的中心频率为f0,其以键控信号频率f为等差级数向两边展开。对FSK信号进行傅里叶变换可得对应的载波频率信息。 2FSK信号的时域和频域波形如图1所示,可以看出,在频域中,2FSK信号有2条谱线。 图1 2FSK信号的时域频域波形图 本文算法以时频二维灰度图为基础,识别调频信号,对其进行边缘检测。信号时频平面中,在瞬时频率附近的信号集中了主要能量,载波处的能量较大。与其他非载波区域相比较,图像的灰度值发生了剧烈变化。对时频二维灰度图进行边缘检测得到的边缘检测图像,包含了信号的主要能量特征,根据这些特性来进行特征提取。 FSK信号的二维信号特征提取步骤描述如下。 步骤1通过DSTFT的得到FSK信号的时频图。求出时频图的灰度,执行幂律变换[7]以获得增强的灰度值矩阵G(i,k)。 步骤2利用矩阵G(i,k)得到增强的时频二维灰度图,进行基于蚁群算法的边缘检测[14]。载波频率边缘处的灰度值发生剧烈变化,得到的边缘检测图包含信号载波信息。 步骤3沿着边缘检测图的纵轴(时间轴)做横轴(频率轴)的投影,得到包含载波个数的曲线图。根据曲线图的最小波谷数确定谱线数。如果曲线有L个波谷,则有L条谱线。谱线向量位置为 D=(d0,d1,…,dL-1)。 (5) 步骤4根据FSK信号时频图的频谱线数,区分出FSK信号的载波频率个数。 令i时刻的白噪声n(i)通过接收机后变成高斯有色噪声n1(i)。以采样率fs进行采样,得到时刻i输出的FSK信号序列函数[7]表达式为 s(i)=x(i)+n1(i), (6) (7) 其中,x(i)为i时刻的FSK信号;A是信号幅度;fn为第n个载波频率;θn为初始相位。g(·)为时刻i的矩形脉冲,Ts为码元宽度。 经过离散短时傅里叶变换(discrete short time Fourier transform, DSTFT),输入信号被转换为离散化的时频平面。选取长度为M的窗函数w(·),以时间作为采样周期,序列信号s(i)在时间点i和频率点k处的DSTFT表达式[7]为 (8) 通过(8)式可以看出,信号的DSTFT实际为加窗函数的离散傅里叶变换,SSTFT(i,k)相当于对信号s(i)截取有限长度做离散傅里叶变换[7]。因此信号s(i)在时间点i的短时功率为 P(i,k)=|SSTFT(i,k)|2。 (9) 不同时刻、频率点处的短时功率谱构成短时功率谱矩阵P(i,k),将其映射为信号s(i)的时频图。 采用经过灰度处理后时频图的灰度深浅表示频谱强度,横轴和纵轴分表表示时间和频率。为了得出时频二维灰度图,需要将短时功率谱矩阵P(i,k)转化为灰度值矩阵。 对矩阵P(i,k)中的每个元素均乘以矩阵P(i,k)中元素的最大值,再乘以255后做取整运算,得到灰度值矩阵H(i,k)。时频二维灰度图可由灰度值矩阵H(i,k)表示。 噪声的影响导致时频二维灰度图的分辨率下降。为了提高图像分辨率,采用幂律变换[16]对图像做增强处理。令像素点(z,r)的灰度值为q,经过幂律变换得到的增强值为 h=c(q+ε)γ。 (10) 其中,c和γ为转换系数,γ值决定了图像增强的效果;ε为偏移量。以此类推,得到图像增强后的灰度值矩阵G,代表图像的增强时频二维灰度图。 灰度值矩阵元素对应灰度图像像素,矩阵元素值代表图像灰度值。基于蚁群的边缘检测算法选取蚂蚁模型,通过启发式信息来判断边缘特性比较明显的像素点。每个像素可以被认为是沿着图像在矩阵中移动的蚂蚁,蚂蚁在边缘处留下信息素。图像梯度变化明显的边缘反映蚂蚁根据启发式信息移动经过的路径。以蚂蚁在图像中留下的访问信息为依据,建立像素矩阵,从而确定图像边缘。 在一幅图像中随机放置蚂蚁l只。利用相邻像素的信息素值计算每个蚂蚁的启发信息。计算出每只蚂蚁向其所在位置相邻8个像素点转移的概率,蚂蚁向转移概率最大的像素点移动。 令ηzr和τzr分别表示像素点(z,r)处的启发信息和信息素浓度,每只蚂蚁移动到一个像素点都会释放信息素,设信息素以挥发率ρ挥发,挥发规则[13]为 (11) (12) 其中,Q为设定阈值,ηzr>Q表示蚂蚁搜索到可能的边界。 当蚂蚁转移到新像素点时,在该点释放新的信息素值,完成一次局部更新;以此类推,当蚁群中所有蚂蚁移动完成后,实现对图像信息素图的全局更新。 每只蚂蚁依据该像素点的转移概率移动位置。设时刻t蚂蚁v从位置(z0,r0)转移到(z,r),转移概率[17]为 (13) 其中:α为信息素启发式因子,影响蚂蚁的路径选择能力;β为期望启发式因子,影响启发信息作用的大小。每只蚂蚁都是以启发信息和信息素图为规则,由当前位置向相邻的8个像素点移动。蚂蚁在完成预定的迭代次数后结束算法。 基于蚁群算法的边缘检测算法流程如图2所示。 图2 蚁群边缘检测流程 为了验证算法的可行性和有效性,采用MATLAB 2014a软件进行仿真。实验采用一台2.50 GHz AMD四核CPU,8G RAM的计算机编写代码,分别模拟2FSK信号和4FSK信号作为测试信号。选择汉明窗进行DSTFT,设置窗函数的长度为100个采样点。 (1)信噪比15 dB条件下2FSK信号的识别 设定码元个数为1 000,载波频率f1、f2分别为2.5 MHz和3 MHz,码速率为300 bit/s,采样频率为10.2 MHz的2FSK信号,混入带宽为1.2 MHz的高斯白噪声,模拟产生信噪比为15 dB的2FSK信号。2FSK信号经过DSTFT变换的时频图、时频二维灰度图、蚁群边缘检测图和投影图,分别如图3—图6所示。 图3中有2个明显的波峰,说明在信噪比15 dB条件下,2FSK信号有2个载波频率。经过多次实验,对时频图进行灰度处理后,取γ值为0.8进行变换,可以得到效果较好的增强图像。信噪比15 dB时的时频二维灰度图及增强图像如图4所示。 从图4可以看出,相比于图4(a),图4(b)能够比较清晰地显示载波信号的边缘,表明图像增强方法对于噪声信号有一定的抑制作用,但是,仍然无法清晰区分载波。对增强的时频二维灰度图做基于蚁群算法的边缘检测,如图5所示。可以看出,进行基于蚁群的边缘检测后,降低了噪声的影响,较好的保留了信号信息,能明显区分载波信号。 图3 信噪比15 dB条件下2FSK信号时频图 (a) 2FSK二维灰度图 (b) 2FSK二维灰度增强图像 图5 15 dB下的2FSK信号蚁群边缘检测图 沿着边缘检测图时间轴做频率轴的投影,得到包含载波个数的曲线,如图6所示。可以看出,投影图曲线显示出2个波谷,则验证了2FSK信号的2个载波频率。 图6 2FSK信号蚁群边缘检测图投影 (2) 15 dB信噪比的4FSK信号 选取4FSK信号载波频率f1、f2、f3和f4分别为2.5 MHz、3 MHz、3.5 MHz和4MHz,采样频率为12 MHz。在信噪比为15 dB条件下的时频图如图7所示。可以看出,与15 dB下的2FSK信号时频图相比,在信噪比为15 dB条件下4FSK信号更加平滑。 图7 15 dB信噪比条件下的4FSK信号时频图 保持转换系数不变,在信噪比为15 dB条件下4FSK信号的时频二维灰度图及增强图像如图8所示。可以看出,由于受到噪声影响,增强的时频二维灰度图不能清晰、有效地区分载波。 对增强后的时频二维灰度图做基于蚁群算法的边缘检测,其结果如图9所示。可以看出,经过边缘检测抑制噪声后,保留了大部分载波信号,提高了分辨载波信号能力。 沿着边缘检测图时间轴做频率轴的投影,得到包含载波个数曲线,如图10所示。可以看出,当信噪比为15 dB,投影曲线有4个很明显的波谷,验证了4FSK信号有4个载波频率。能够明显地区分4FSK载波信号。 (a) 4FSK二维灰度图 (b) 4FSK二维灰度增强图像 图9 15 dB下的4FSK信号蚁群边缘检测图 图10 4FSK信号蚁群边缘检测图投影 为了在不同信噪比条件下验证算法的稳定性,以4FSK信号为例,信噪比范围选取10 dB到30 dB,步进为2 dB,在每个信噪比条件下进行500次实验,得到每个信噪比条件下信号载波频率个数的统计数据。计算每个信噪比条件下载波频率个数的平均值,得到载波频率的实际个数,如表1所示。可以看出,信噪比从10 dB递增到30 dB时,4FSK信号的理论载波频率个数和实际载波频率个数一致,表明算法具有一定的稳定性。 表1 不同信噪比下的载波频率个数 在相同实验条件下,与文献[7]算法进行比较,两种算法识别率的相对误差如图11所示。 图11 不同算法的相对误差 由图11可以看出,本文算法识别率的相对误差低于文献[7]算法,但是,随着信噪比增大,两种算法识别率的相对误差逐渐接近。这可能是因为,与文献[7]以特征参数角二阶矩(angular second moment,ASM)能量曲线区分信号载波频率个数的方法相比,本文算法对时频图做基于蚁群的边缘检测,能够更清晰地描述出载波和非载波区域边缘,明显地区分载波频率个数,从而有效地减少噪声干扰,提高了识别的准确性。 提出一种基于时频图蚁群边缘检测的调频信号识别算法。该算法在传统时频分析的基础上,对增强的时频二维灰度图做基于蚁群的边缘检测;对边缘检测图投影,得出包含载波个数的曲线,区分载波频率的个数。通过仿真实验表明该算法能有效地区分2FSK信号和4FSK信号载波频率个数。性能实验表明,在信噪比10dB~30dB下,算法不受信噪比变化的影响,具有一定的稳定性。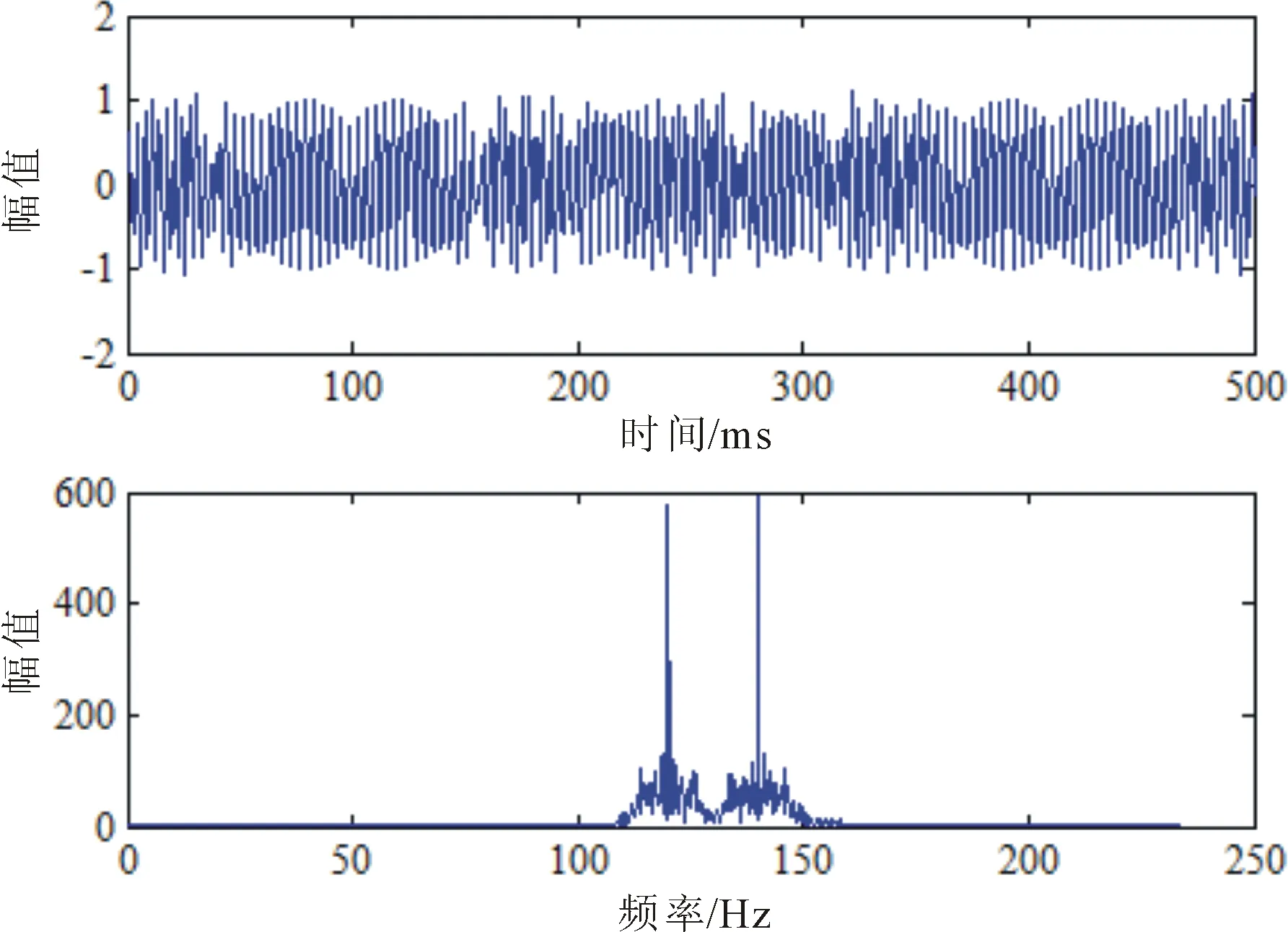
2 FSK信号的二维信号特征提取
2.1 算法步骤
2.2 生成时频二维灰度图
2.3 基于蚁群算法的边缘检测
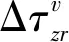

3 实验及结果分析
3.1 调制方式识别仿真实验






3.2 不同信噪比条件下算法的性能
4 结语

