一类不可微优化问题的混合萤火虫算法
李琳娜, 方 铭, 黄琼丹
(1.西安邮电大学 校友工作办公室, 陕西 西安 710121; 2.西安邮电大学 计算机学院, 陕西 西安 710121;3. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
l1模极小化问题已广泛应用在稀疏信号处理和机器学习领域[1-4]。利用混合l1/l2范数最小化和正交匹配追求算法,设计了多输入多输出系统中稀疏有限脉冲响应决策反馈均衡器[1];利用顺序重加权l1范数最小化技术,研究了电子冷却问题中二维热传导的热源分布优化问题[3];将波束发生器输出向量的l1模,作为成本函数的波束形成方法[4]。由于l1模极小化问题是不可微优化问题,求解较为困难。利用凝聚熵函数法[5-7],将l1模极小化问题转化为可微优化问题,可求解非线性l1模极小化问题,但此方法仅适用于求解连续性、可微分和小规模等问题[8-11],对于目标函数及约束函数非光滑的问题,则需要不断计算待求解问题的梯度信息并选取合适的初始点作为计算起点,求解难度大[7]。
萤火虫算法[12-14](firefly algorithm,FA)是一种群体智能算法,具有不依赖于初始点选取和梯度信息等特点,可解决离散性、不确定性和大规模等问题,跟粒子群算法[15](particle swarm optimization,PSO)相比,收敛速度更快,已广泛应用在人工智能、目标优化和系统控制等领域。
为了解决非线性l1模极小化问题,本文提出一种改进的l1模极小化萤火虫算法(l1firefly algorithm,LFA)。通过凝聚熵函数法及罚函数法[7],将非线性l1模极小化问题转化为光滑函数的无约束优化问题[8],并应用萤火虫算法进行优化求最优解。
1 问题描述
非线性l1模极小化问题可描述为
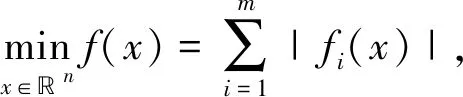
(1)
其中,fi(x)是一簇光滑函数(i∈+),gj(x)是一簇光滑约束函数。由于绝对值函数的不可微性,导致此问题的目标函数f(x)是不可微函数,所以问题(1)是较为复杂的带约束不可微优化问题。
将函数f(x)等价为
构造函数f(x)的凝聚熵函数,通过引入下述相关定义及定理[7-8],可将非线性l1模极小化问题转化为可微优化问题。
定义1定义函数

为问题(1)中目标函数f(x)在x∈n上的凝聚熵函数,p为可调节参数。
定理1对任何x∈n,函数Fp(x)随参数p的增大而单调减少,且当p→+∞时,以f(x)为极限,即
Fs(x)≤Fr(x)s≤rs,r∈
由定理1可知,当p取的足够大时,函数Fp(x)可近似替代目标函数f(x)。因此,当p→+∞时,问题(1)可近似为
minFp(x)
s.t.gj(x)≤0(j=1,2,…,n;x∈n)。
(2)
问题(2)中目标函数可微,但是约束函数仍不可微。因此,对约束函数进行处理,可将问题(2)转换为目标函数与约束函数均可微的优化问题。
定理2问题(2)的约束集合等价于极大值约束
定理2把多约束问题转化为单约束问题,则问题(2)可等价于
minFp(x)
s.t.G(x)≤0。
(3)
定义2定义函数
为函数G(x)在x∈n上的凝聚熵函数,q为可调节参数。
定理3对任何x∈n,函数Gq(x)随参数q的增大而单调减少,且当q→+∞时,以G(x)为极限,即
Gs(x)≤Gr(x)s≤rs,r∈,
由定理3可知,当q取的足够大时,函数Gq(x)可近似替代目标函数G(x)。因此,当q→+∞时,问题(3)可近似为
minFp(x)
s.t.Gq(x)≤0,
(4)
此时,问题(4)中的目标函数与约束函数均光滑可微,便于问题求解。当p,q→+∞时,可用问题(4)的解近似代替问题(1)的解。
定义3称函数
φ(x,η)=Fp(x)+ηGq(x),
(5)
为问题(4)的罚函数,η为罚因子。
式(5)将问题(4)转化为无约束可微优化问题,以式(5)作为目标函数,利用萤火虫算法极小化该目标函数,在参数选取合理情况下,便可得到问题(4)的解,即问题(1)的高精度近似解。
对于无约束非线性l1模极小化问题,只需利用萤火虫算法极小化问题(2)中的目标函数Fp(x),即可求得问题(1)的高精度解。
2 萤火虫算法
萤火虫算法[16-18]是一种启发式群智能优化算法,其灵感来自于萤火虫荧光闪烁的求偶行为。在萤火虫算法中,个体之间存在自身亮度和吸引度两个要素。个体自身亮度由其当前适应值决定,适应值越佳,自身亮度越高,所处位置就更优。吸引度与亮度相关,亮度越高的个体吸引力更强,可以吸引亮度更弱的个体向自身靠近,如果亮度相同,则各自随机移动。吸引度决定了个体在每次迭代中,靠近吸引个体移动的距离大小。为了符合自然界中光线传播衰减规律,个体之间的相对亮度与吸引度和个体之间距离成反比。将个体所在位置坐标作为潜在解,利用发光特性,吸引视线内萤火虫相互靠近和移动,从而实现个体的位置更新,搜索最优解。
从数学角度考虑萤火虫算法,需要定义荧光的相对亮度、个体的吸引强度及位置更新公式等3个参数[12-13]。
定义4荧光的相对亮度
L=L0×e-βrij,
(6)
其中L0表示个体的最大荧光亮度,即rij=0处的萤光亮度,与适应值函数有关。β为光强度吸收因子,模拟光线传播中的衰减现象,可设为常数。rij为个体i与j之间的直线距离,计算表达式为
(7)
其中,xik与xjk分别表示第i个个体与第j个个体位置的第k维坐标,n为空间维数,即问题变量个数。
定义5个体的吸引强度
σ=σ0×e-βrij,
(8)
其中σ0为最大吸引强度,即rij=0处的吸引强度。
定义6个体的位置更新公式为
xik=xik+σ(xjk-xik)+α(R-1/2),
(9)
其中α为步长,R为[0,1]均匀分布的随机数。为了避免早熟收敛,加入随机扰动因子α×(R-1/2)。α为线性递减,在算法运行初期,可增强全局搜素能力;后期则利于局部精细搜索。
3 LFA算法
LFA算法利用凝聚熵函数将非线性l1模极小化问题的目标函数及约束函数分别转化为单一光滑函数,构造此光滑目标函数与光滑约束函数的罚函数,再利用萤火虫算法极小化该函数并求得最优解。具体算法步骤如下。
步骤1算法初始化,给出光强度吸收因子β、p、步长α和最大荧光亮度σ0等基本参数,其中罚因子η>0。
步骤2在n维空间,随机生成个体m的位置坐标。
步骤3计算第k代每个个体的目标值φ(x(k)η(k)),设置为各自最大荧光亮度L0。
步骤4根据式(6)、式(7)和式(8),分别计算每个个体的相对荧光亮度L和吸引强度σ,并由相对荧光亮度决定个体移动方向。
步骤5令k=k+1,根据式(9)更新个体位置。
步骤6当满足停止准则时,转步骤7,否则,转步骤3,进行新的搜索。
步骤7输出个体所在位置坐标。
求解凝聚熵函数Fp(x)和Gq(x)时,当参数p,q选取过大,则会引起指数部分过大,导致数据溢出,无法得到结果输出;若p,q取值较小,则计算精度得不到有效保证,因此作以下处理。
取临界正整数M,使eM+1发生数据溢出,且eM未发生。
(1)对函数Fp(x),令
若pFk(x)≤M,则

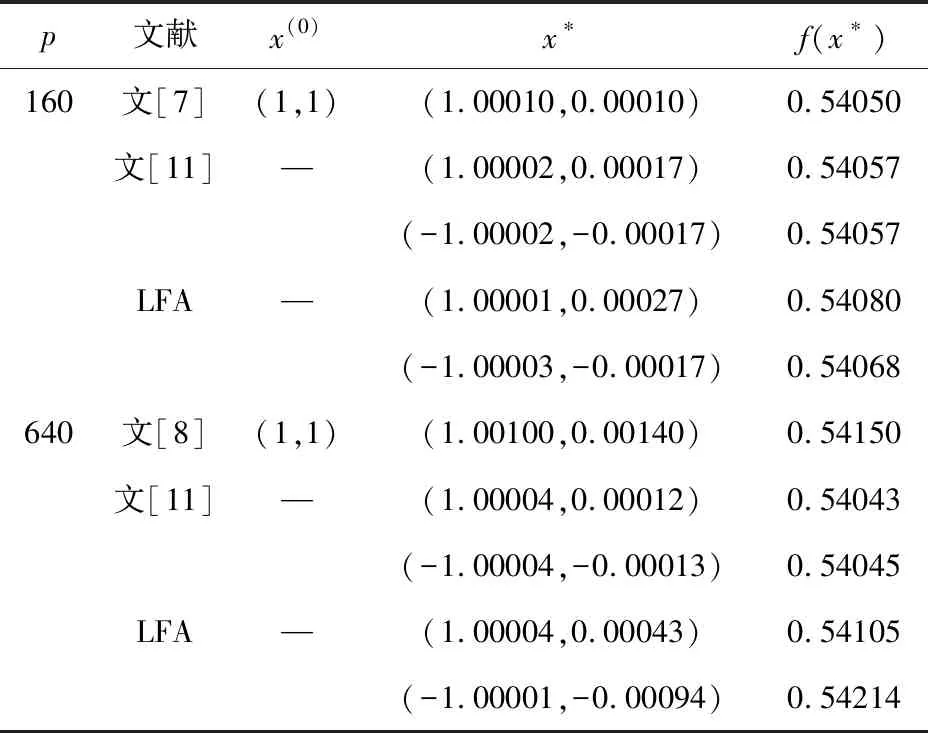
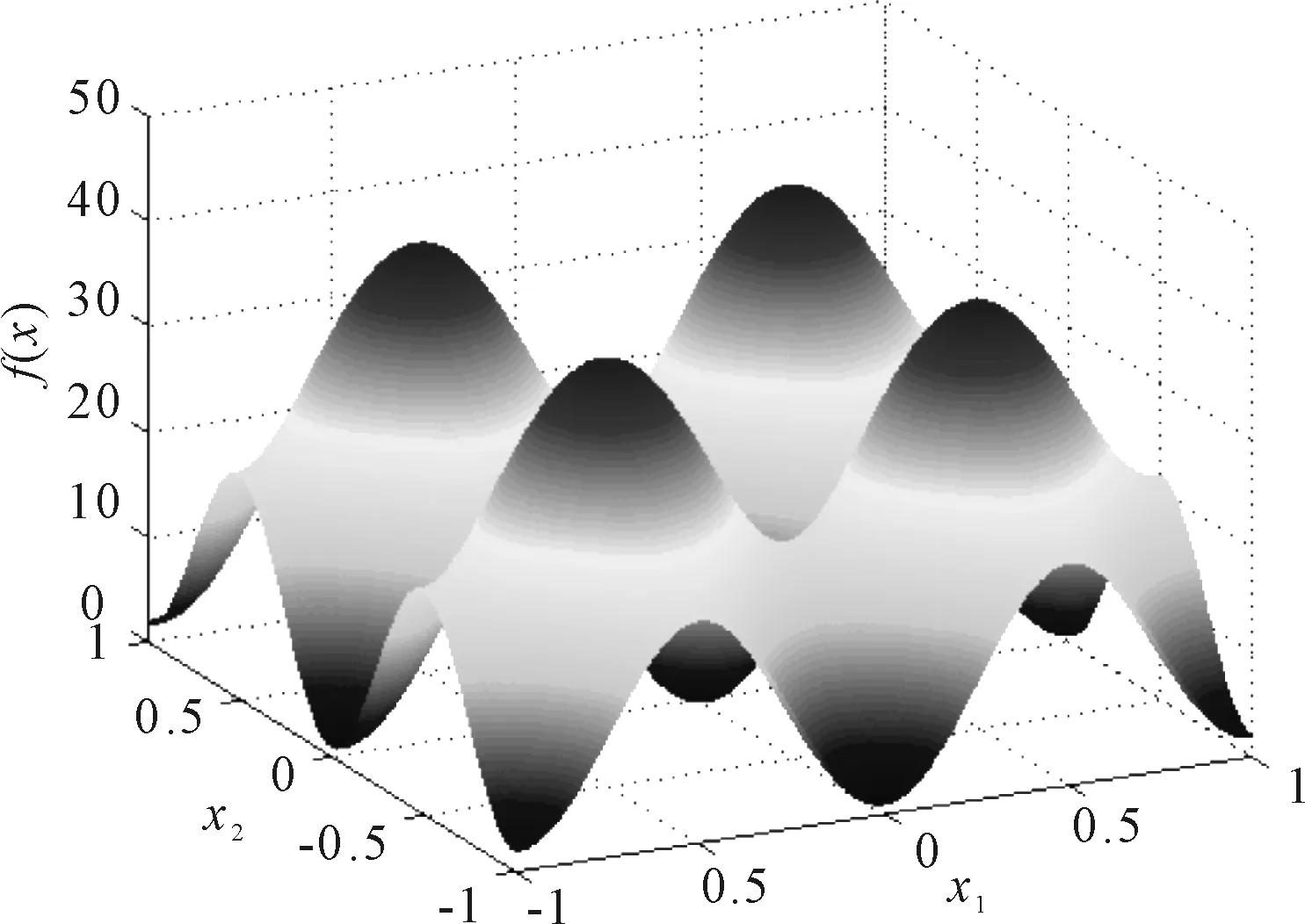
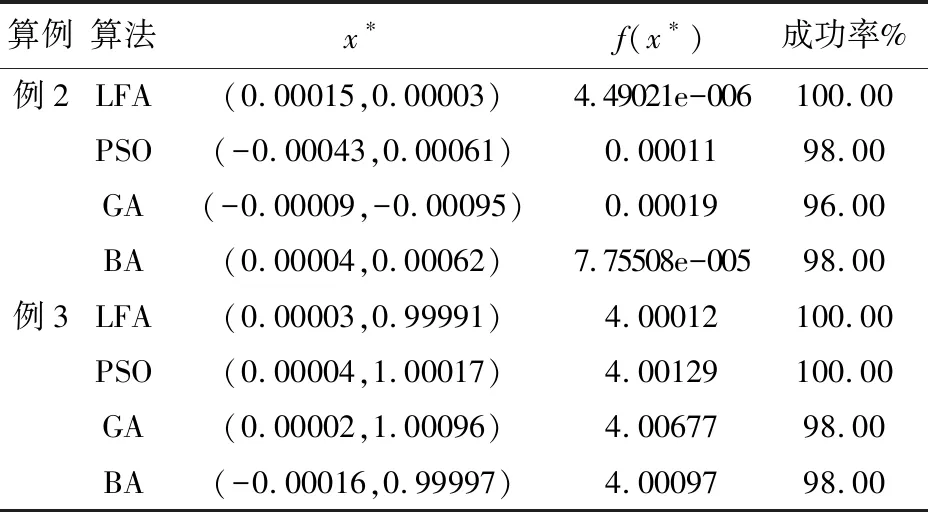
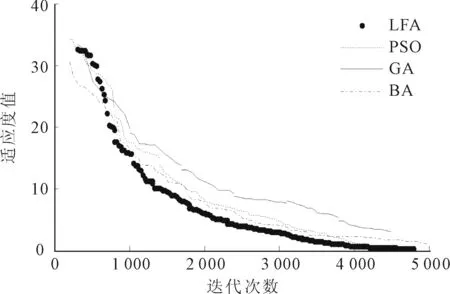
若pFk(x) (2)对函数Gq(x),令 若qGk(x)≤M,则 若qGk(x)>M,则 Gq(x)=±Gk(x), 其中,当Gq(x)为正时,右式取“+”号,当Gq(x)为负时,右式取“-”号。 LFA算法的性能主要由凝聚熵函数调节参数的取值和搜索解的能力两个方面因素决定,实验分别对这两个因素进行探讨。 实验平台为Windows 10、64位操作系统,因特尔i3双核、64位处理器,主频1.7Ghz,4G内存,实验所涉及算法使用C++语言编程实现。 例1问题 最优解 x*=(1,0)T,f(x*)=cos 1, 或者 x*=(-1,-0)T,f(x*)=cos (-1) 例2问题 最优解 x*=(0,0)T,f(x*)=0 例3问题 最优解 x*=(0,1)T,f(x*)=4 实验1验证调节参数p对LFA算法性能的影响。例1是无约束非线性l1模极小化问题,算法精度ε=10-6,个体数m=100,空间维数n=2,最大吸引度σ0=1.0,光强吸收因子β=1.0,步长α=0.5,解的空间范围限定在[-1,+1]。分别对比p取不同值时,文献[7]、文献[8]、文献[11]和LFA算法的求解结果,如表1所示。 表1 不同p值对比结果 由表1可知,文献[7]与文献[8]算法求解初期,需要设置初始点x(0),对于不同的初始点,求解的最优点可能会不同,这是由于在求解梯度时,梯度下降方向唯一造成的。若选取不当的初始点,则会对最后的计算结果产生较大影响,甚至造成错解或者漏解。例1有一对对称解,文献[7]与文献[8]算法均发生了漏解现象。文献[11]求解此问题时,与LFA算法均属群体智能算法。在p取值相同的情况下,LFA算法求解精度比文献[7]和文献[8]较高,同时,不依赖于初始点的选取,所以不会产生漏解现象。当p值增大,例1的解都更加精确,因此,在实际解决此类问题时,p的取值应当更大。 图1 例2函数图像 算例算法x∗f(x∗) 成功率%例2LFA(0.00015,0.00003)4.49021e-006100.00PSO(-0.00043,0.00061)0.0001198.00GA(-0.00009,-0.00095)0.0001996.00BA(0.00004,0.00062)7.75508e-00598.00例3LFA(0.00003,0.99991)4.00012100.00PSO(0.00004,1.00017)4.00129100.00GA(0.00002,1.00096)4.0067798.00BA(-0.00016,0.99997)4.0009798.00 由表2可以看出,对于复杂的非线性l1模极小化问题,以上4种群体智能算法均能取得满意解,但LFA算法对待优化问题进行了熵函数处理,使待求解函数变的光滑,搜索成功率也高于其他3种算法。图2和图3分别为例2和例3的收敛曲线,可以看出,LFA比其他3种算法下降的更快,因此收敛速度较快。 图2 例2收敛曲线 图3 例3收敛曲线 LFA算法不依赖初始点信息,且无需梯度信息,采用凝聚熵函数法及罚函数法将非线性l1模极小化问题转化为光滑函数的无约束优化问题,再利用萤火虫算法进行优化搜索最优解。数值实验结果表明,LFA算法的求解精度和搜索成功率均比PSO算法、GA算法和BA算法高,可有效求解非线性l1模极小化问题。4 数值实验对比及结果分析
4.1 数值算例
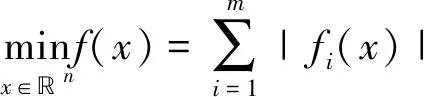
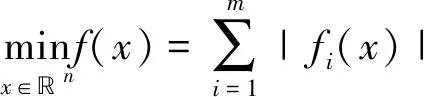
4.2 实验分析
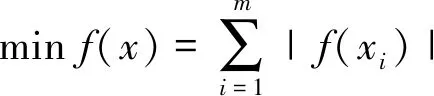

5 结语

