基于遗传神经网络的学生成绩预测
刘 毓, 杨 柳, 刘 陆
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
为了提高教学质量,制定合理化的人才培养方案,众多学者开始关注数据挖掘技术在教育教学领域的应用[1]。教育数据挖掘[2]是指用数据挖掘技术分析从大量教学数据中自动检索并整理统计出相关信息的数据分析过程,发现教学数据中潜在的有效信息,以解决教学实践中的问题,为教学管理者、教师、学生等教育领域相关人员提供教学建议和理论支持。学生成绩预测是教育数据挖掘中的重要内容。
目前,基于遗传神经网络的成绩预测的研究大致可分为如下几类,径向基函数神经网络预测(radial basis function, RBF)、反向传播神经网络预测(back propagation, BP),以及成绩修正模型预测等。文献[3]提出了基于主成分分析法-径向基函数(principal component analysis-radial basis function, PCA-RBF)神经网络的学生成绩预测模型,使用主成分分析法(principal component analysis, PCA)进行数据降维,利用RBF神经网络进行学生成绩预测,虽然提高了预测精度,但未得出学生成绩的影响因子,使该模型的可理解性降低[4]。文献[5]利用BP神经网络对学生成绩进行预测,但BP神经网络的预测精度较低[6]。文献[7]提出了一个学生等级预测模型,利用基于特征选择回归和BP神经网络的方法进行等级预测,为学生成绩分析提供了重要参考,但是该模型的预测精度不足[8]。文献[9]提出了一种基于试卷难度系数变化的GM(1,1)修正模型,仅以试卷难度系数为标准,对学生考试成绩进行预测,模型实用性不足[10]。
为了提高学生成绩预测的精度,本文拟提出一种基于遗传神经网络的学生成绩预测模型。该模型通过计算相关系数来简化输入项,引入遗传算法优化BP神经网络的初始权值和阈值,改进BP神经网络预测模型,实现对学生成绩的预测。
1 BP神经网络学生成绩预测
BP神经网络是多层前向网络,包括输入层、隐含层和输出层共3层,如图1所示。输入层主要负责接收信号,隐含层对信号进行映射转换,输出层主要输出BP神经网络的预测结果。
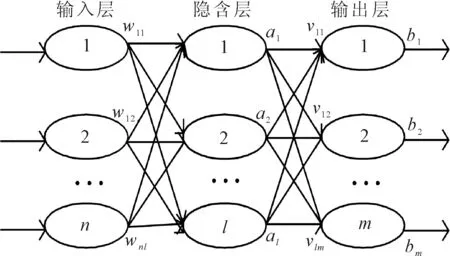
图1 3层BP神经网络结构
其中,假设n是输入层节点数,l是隐含层节点数,m是输出层的节点数,{w11,w12,…,wnl}分别为连接输入层节点与隐含层节点之间的权值,{a1,a2,…,al}分别为隐含层每一个节点上的阈值,{v11,v12,…,vlm}分别为连接隐含层节点与输出层节点之间的权值,{b1,b2,…,bm}分别为输出层每一个节点上的阈值。BP神经网络主要采用误差函数梯度下降法进行学习,循环进行输入信号的前向传播和误差的逆向传播这两个过程,直到均方误差值等于给定值或达到最大迭代次数为止[11]。
分别对BP神经网络的输入层节点数、隐含层节点数以及输出层节点数进行设置。输入层的节点数为输入的课程数目,输出层的节点数取决于输出的课程数目。隐含层节点数采用试凑法确定,根据实验结果选择最优的隐含层节点数。利用试凑法[12]对隐含层的初始值确定式为
(1)
式中∂是1~10之间的任意常数。建立BP神经网络预测模型,输入数据为某高校通信工程专业的学生基础课程成绩,输出数据为学生的核心专业课程期末考试成绩。
2 遗传神经网络学生成绩预测
为了克服BP神经网络建立预测模型预测精度低的缺点[13],建立了一种基于遗传神经网络的预测模型,如图2所示。

图2 遗传神经网络预测模型
通过相关分析法[14]选择与预测目标课程成绩高度关联的基础课程成绩作为预测的输入项,引入遗传算法优化BP神经网络的权值和阈值,选择、交叉、变异为BP神经网络选择最优的初始权值和阈值。遗传神经网络预测学生成绩的具体流程,如图3 所示。
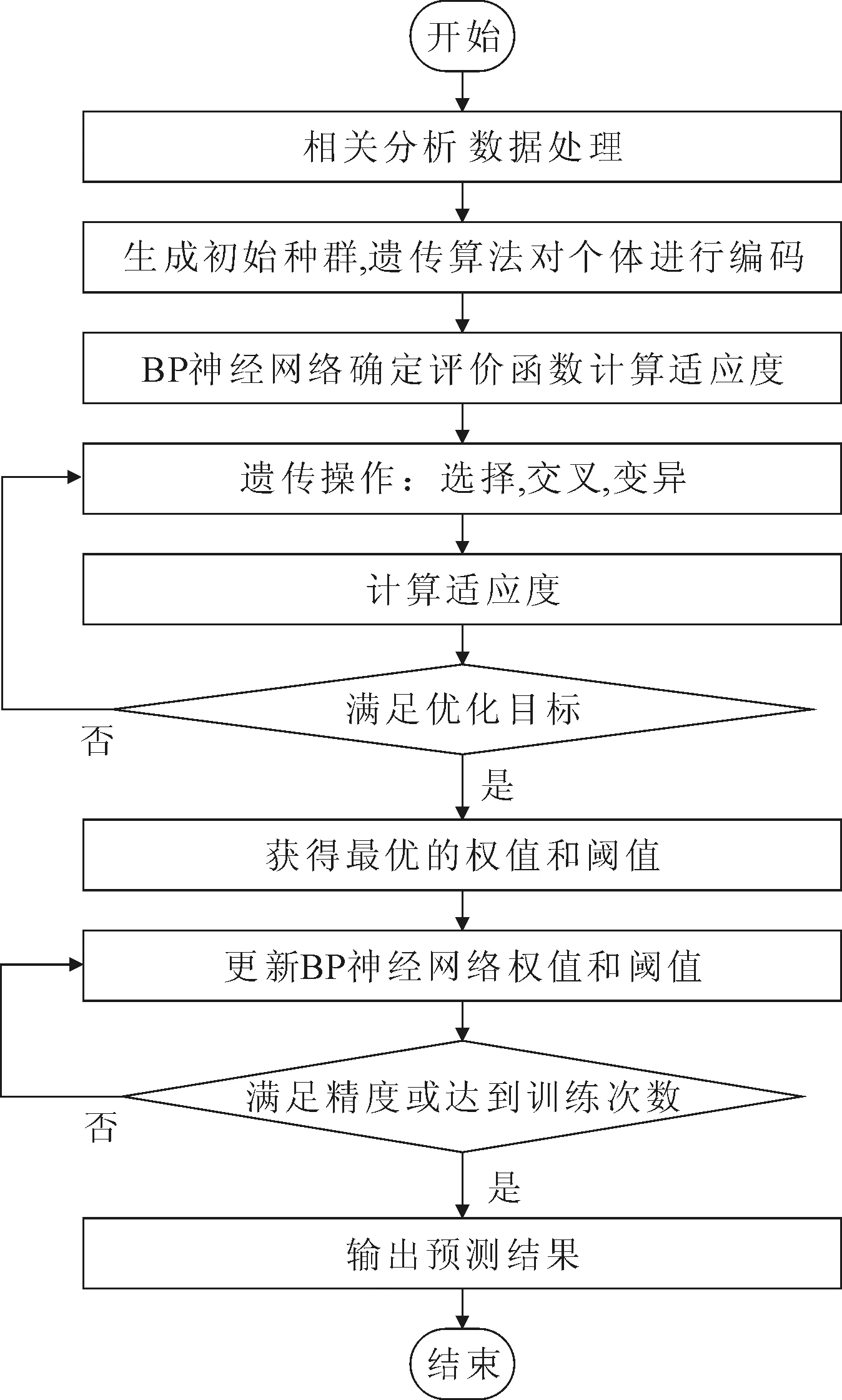
图3 遗传神经网络成绩预测流程
2.1 相关分析法
相关分析法[14],是研究观测值之间是否存在某种依存关系,并探讨具有依存关系的变量之间相关方向、相关程度,分析随机变量之间相关关系的一种统计方法。用相关分析法计算基础课程成绩与目标课程成绩的相关性,分析各门基础课程成绩对目标课程成绩的影响程度。
在相关分析法中,一般使用皮尔逊相关系数[14]ρ来研究相关度,其定义[14]为
(2)
2.2 遗传算法优化BP神经网络
遗传算法是基于自然群体遗传进化机制的自适应全局优化概率搜索算法,它模拟了生物进化中的繁殖、杂交和突变现象[15]。遗传算法优化BP神经网络,主要利用BP神经网络中的初始权值和阈值作为遗传算法中的染色体,生成初始种群,用遗传算法的遗传算子进行选择、交叉和变异操作,对种群个体进行逐代择优,找到BP神经网络的初始权值和阈值的最优解并进行赋值,代入BP神经网络模型训练,得到全局最优预测值,降低BP神经网络的预测误差。
2.2.1 实数编码
采用实数编码的方式设计神经网络,将BP神经网络中的所有权值和阈值作为待编码的参数,待编码的参数为(n+1)×l+(l+1)×m,这些参数的排列顺序为输入层到隐含层的权值,隐含层到输出层的权值,隐含层的阈值,输出层的阈值。
2.2.2 适应度函数
遗传算法搜索目标为获取所有进化代中使网络的误差平方和最小的网络权值和阈值,遗传算法朝着适应度函数值增大的方向进化[12],适应度函数f可以用每一个个体的训练误差的倒数来表示
(3)
式中oi是通过BP神经网络预测输出的学生的目标课程成绩数据。
2.2.3 选择算子
采用轮盘赌法[12]的选择方式,首先计算某代个体的适应度值fc,然后计算此适应度值在总适应度值中所占的比例,用K表示种群个体的数目,c(c=1,2,..,K)为种群K中的一个个体,则该个体在选择过程中被选择的概率为Pc
(4)
2.2.4 交叉操作
从种群中选择两个个体,按照给定的概率交叉,得到新个体的操作称为交叉操作[16]。采用实数交叉法进行交叉操作,r是染色体,h、v是染色体的个数,s是染色体的位数,第h个染色体rh和第v个染色体rv在第s位的交叉操作[16]方法为
(5)
式中rhs是第h个染色体的s位,rvs是第v个染色体的第s位,β为[0,1]之间的随机数。
2.2.5 变异操作
从种群中随机选择一个个体,按一定概率变异,得到新个体的过程叫做变异操作[16]。例如第h个染色体的第s位进行变异,变异方法[16]为
rhs=rhs+Δx。
(6)
式中Δx为随机数,设Δx的取值范围[rmin-rhs,rmax-rhs],rmax是基因rhs的上界,rmin是基因rhs的下界。
用遗传神经网络进行学生成绩预测,将学生课程成绩分为学习样本与测试样本,学习样本中的基础课程成绩设置为遗传神经网络的输入项,目标课程成绩设置为输出项,用学习样本训练遗传神经网络模型,将测试样本中的基础课程成绩代入训练好的模型中,即可预测得出的学生的目标课程成绩,实现对学生成绩的预测。
3 实验结果及分析
3.1 数据采集
采集数据为某大学通信工程专业1601—1603的99名学生,在大学一年级和大学二年级两年中的12门基础课程成绩,分别为高等数学AI、高等数学AII、大学物理AI、线性代数A、复变函数、大学物理实验AI、电路分析基础A、电路基础实验、大学英语I、大学英语II、思想道德修养与法律基础、大学体育的成绩,并采集这些学生的核心专业基础课信号与系统的期末考试卷面成绩。
针对采集的原始数据,做数据预处理,删除在本次考试中缺考学生的所有数据,剩余80名学生数据,再将数据归一化至[0~100]区间内,得到最终的学生成绩数据。
3.2 相关分析法数据处理
将信号与系统作为预测目标课程,参照式(2),可得到经数据预处理后的通信工程专业80名学生的12门基础课程成绩,与目标课程信号与系统成绩之间的相关系数,见表1。
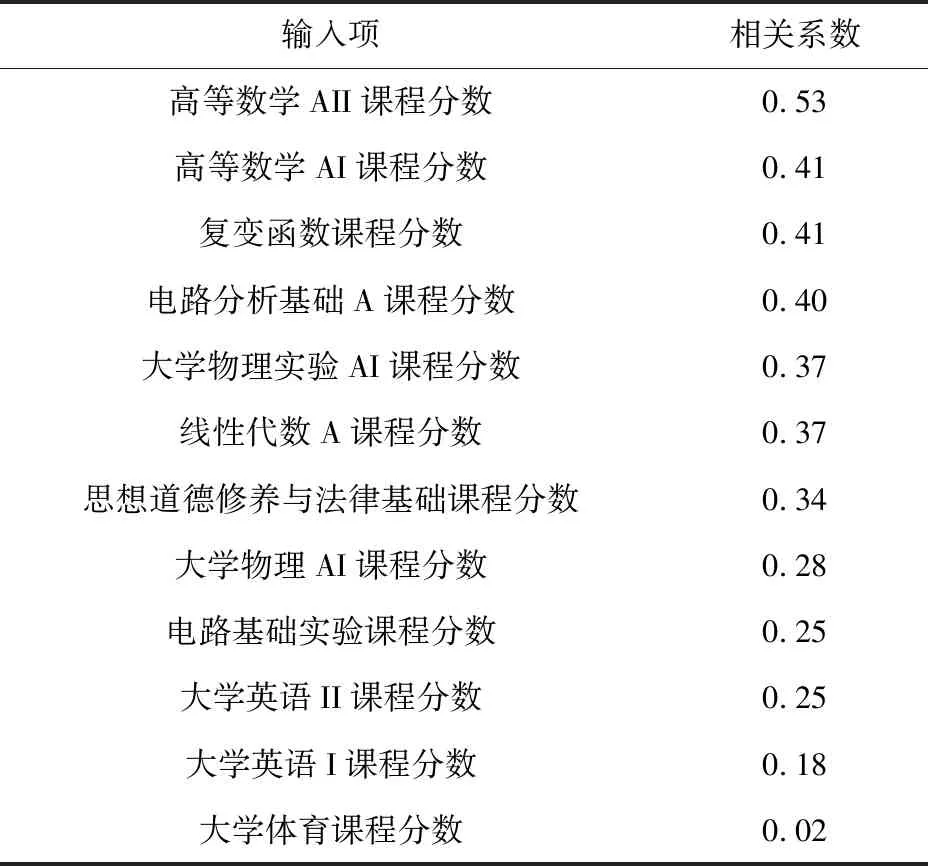
表1 基础课程与目标课程相关系数
表1中可以看出,高等数学AII、高等数学AI、以及复变函数等课程成绩与目标课程信号与系统成绩的相关度较高,而大学体育、大学英语I、大学英语II等课程成绩与目标课程成绩的相关度则相对较低。
3.3 学生成绩预测实验分析
选取matlabR2016a软件作为仿真工具,分别采用BP神经网络模型和遗传神经网络模型进行预测。设置测试集和训练集,将所采集到的通信工程专业1601—1603班级中学号后10位的学生成绩作为测试集,其余70名学生的成绩数据作为训练集。
3.3.1 BP神经网络学生成绩预测分析
使用BP神经网络模型进行学生成绩预测,初始的学生基础课程成绩共12门,将神经网络的输入层神经元设置为12,信号与系统的成绩数据作为输出,将输出层神经元设置为1,根据式(1)可求得,隐含层神经元个数为4~14,由于隐含层的节点数目决定了神经网络结构的非线性映射能力,为了使神经网络具有更好的预测性能,设隐含层神经元为14,设循环次数为3 000,训练误差为0.001。学习速率决定了训练过程中的权值变化,一般情况下选取较小的学习速率保证学习的稳定性,因此这里取学习速率为0.2[5],得到如图4所示BP神经网络模型的实际值和预测值折线图。

图4 BP神经网络模型实际预测值折线
对BP神经网络模型得到的实际值和预测值进行分析。学生1的信号与系统成绩为60分,预测得到68分;学生2的真实成绩为66分,预测得到56分;学生3的实际得分为80分,预测得到72分;学生4的真实成绩为64分,预测得到73分;学生5的真实成绩为72分,预测得到68分;学生6的真实成绩为75分,预测得到61分;学生7的真实成绩为68分,预测得到59分;学生8的真实成绩为56分,预测得到52分;学生9的真实成绩为88分,预测得到77分;学生10的真实成绩为72分,预测得到70分。由于部分输入项与与输出项的相关度低,随机设置了BP神经网络的初始权值和阈值,每个学生得到的预测成绩和和真实成绩都存在较大误差,可以看出BP神经网络模型在学生成绩预测中还存在不足之处。
3.3.2 遗传神经网络学生成绩预测分析
在遗传神经网络的成绩预测中,采用相关分析法选取相关系数大于0.35的高等数学AII、高等数学A、复变函数、电路分析基础A、大学物理实验AI、线性代数A,6门基础课程成绩作为输入项,所以将神经网络的输入层神经元设置为6,将隐藏层神经元设置为13,信号与系统的成绩数据作为输出项,将输出层神经元设置为1,用Matlab仿真工具实现遗传算法的编解码函数和适应度函数,将神经网络部分的参数与BP神经网络的参数设置为相同值,同时对遗传算法种群的初始化和基本参数进行设置,遗传算法中的种群规模一般设置范围为10~200,若种群规模设置过大,导致结果收敛性能差,若种群规模过小,则会出现近亲交配,产生病态基因,因此设置初始种群规模为100,最大遗传代数为50,交叉概率设置范围为0.3~0.9,若交配概率过大容易错失最优个体,交配概率过小则不能有效更新种群,设交叉概率为0.5,变异概率设置范围为0.001~0.2,为了保证种群的多样性同时不破坏现有的种群模式,设变异概率为0.01[11],得到遗传神经网络模型实际值和预测值折线图,如图5所示。
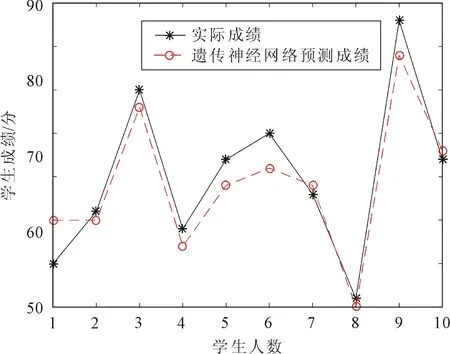
图5 遗传神经网络模型实际预测值折线
图5中可以看出,学生1的信号与系统成绩为60分,预测得到65分;学生2的真实成绩为66分,预测得到65分;学生3的实际得分为80分,预测得到78分;学生4的真实成绩为64分,预测得到62分;学生5的真实成绩为72分,预测得到69分;学生6的真实成绩为75分,预测得到71分;学生7的真实成绩为68分,预测得到69分;学生8的真实成绩为56分,预测得到55分;学生9的真实成绩为84分,预测得到77分;学生10的真实成绩为72分,预测得到73分。遗传神经网络模型预测得到的学生成绩,与学生的实际成绩更为接近。将BP神经网络模型的预测结果与遗传神经网络模型的预测结果进行对比,可以看出遗传神经网络模型具有更小的预测误差,两种模型的预测值对比,见表2。
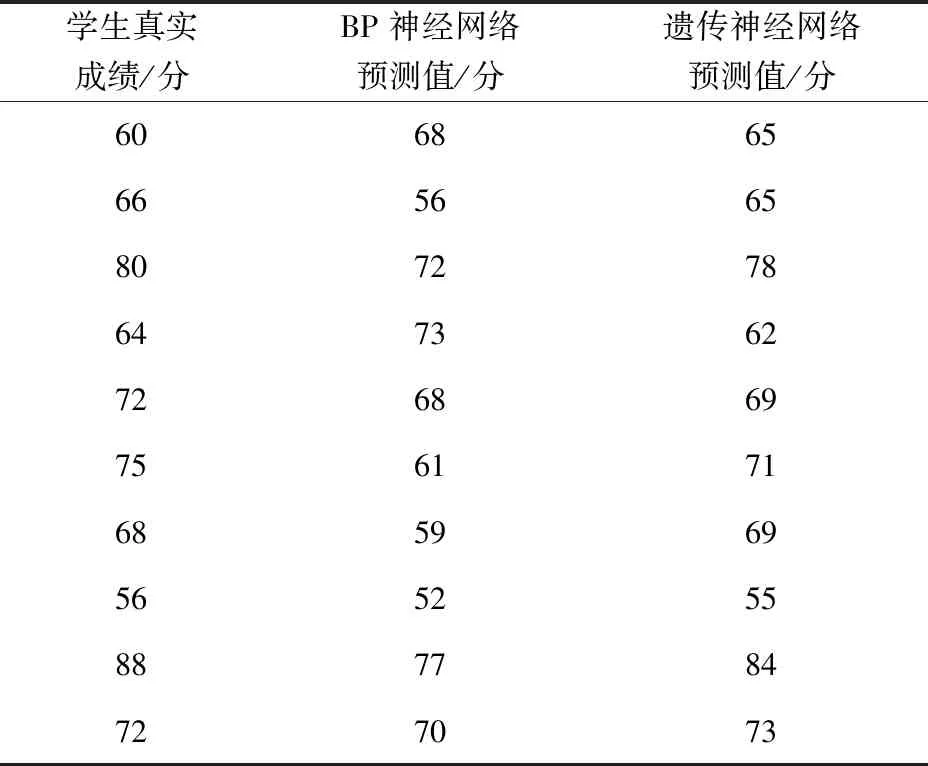
表2 两种模型预测结果对比
根据表2中的两种模型预测值和实际值分别求解两种模型的均方根误差e
(7)
式中Q为预测的学生人数,在本文中为10。
将表2中学生真实成绩作为yi,分别将BP神经网络预测成绩及遗传神经网络预测成绩作为oi,代入式(7)求解出BP神经网络模型预测的均方根误差为8.6,遗传神经网络模型预测的均方根误差为2.8。通过对均方根误差的比较,可以看出,遗传神经网络模型相较于BP神经网络模型,预测精度更高。更适合于进行学生成绩预测。
4 结语
针对遗传神经网络的学生成绩预测,在BP神经网络预测模型的基础上,用相关分析法求解基础课程成绩与目标课程成绩的相关系数,去除与目标课程成绩相关程度低的基础课程成绩,设计遗传算法的编码方式、适应度函数、遗传算子,将遗传算法与BP神经网络相结合,得到BP神经网络的最优初始权值与阈值,建立了遗传神经网络学生成绩预测模型。通过采集某大学通信工程专业1601—1603班级99名学生的实际基础课程成绩,代入遗传神经网络学生成绩预测模型,预测这些学生的核心专业基础课程成绩。实验结果表明,该模型与BP神经网络模型相比,预测的均方根误差由8.6降低为2.8,具有更高的预测精度,验证了该模型的有效性。

