基于CART决策树的HEVC帧间CU快速划分算法

唐浩漾, 王 婧, 孙梓巍, 段一伟

(西安邮电大学 自动化学院， 陕西 西安 710121)

高效视频编码(high efficiency video coding，HEVC)[1]是新一代视频编码标准。相同感知质量下，HEVC比H.264的比特率降低50%，但其编码复杂度也随之提高。在帧间编码过程中，HEVC采用四叉树划分结构提高编码性能，编码单元(coding unit，CU)的尺寸由H.264的16×16变为从8×8到64×64，增加了整个帧间编码过程的复杂度。因此，在不影响HEVC编码性能的情况下，降低帧间编码复杂度是HEVC的主要研究方向之一。

针对HEVC帧间编码中CU划分过程率失真代价计算量大的问题，一些学者提出了在CU划分过程中提早预判CU深度级的算法。如采用预测相邻CU深度率失真代价模型[2]，在编码当前CU深度后快速预测下一深度级CU的率失真代价；或者根据不同深度下CU划分和不划分率失真代价的值，实现对不同深度CU的划分和裁剪，避免了对每一深度级CU率失真代价的计算[3]。但是，这些算法仍需计算率失真代价，计算量较大。

为了避免了率失真代价计算，近年来，一些学者采用机器学习的方法实现对CU的划分。基于贝叶斯和支持向量机的方法[4-5]解决CU的划分问题，虽然能够降低了编码计算复杂度，但是，该方法因误判特征属性导致CU划分结果不够准确。基于决策树的CU快速划分算法[6]以选择CU纹理特征中的最优特征属性作为判断依据，对CU实现快速划分，取得了较好的效果，却在属性特征的选择上忽略了CU时空域相关性的影响。

为了在保持编码性能同时，又能避免率失真代价的计算，本文拟提出一种基于CART决策树算法。该算法利用CU深度存在的空间相关性，建立CART决策树模型，然后用CART模型实现对当前CU的快速划分。最后，采用实验方法验证算法的有效性。

1 HEVC帧间CU划分

在HEVC过程中,CU划分可以分为正向划分与逆向裁剪两个过程[7]，CU是编码的基本单元，其依次采用的大小尺寸有64×64、32×32、16×16和8×8，对应的深度信息D分别取值0、1、2、3。首先进行正向划分过程，从最大编码单元(largest coding unit，LCU),尺寸为64×64开始，每个LCU被划分为4个尺寸均为32×32的CU，以此类推，直至被划分到尺寸为8×8的CU为止，其划分结果如图1所示。然后，进行逆向裁剪过程。如果4个四叉树划分图尺寸CU的率失真代价之和小于其对应的16×16尺寸CU的率失真代价，则保留8×8尺寸CU的分割状态；否则，剪掉此分支。按照这种方式，逐级向上处理，直至64×64尺寸对应的CU。率失真代价是编码的码率与图像失真度之间的相互关系被定义为

J=(Sluma+ωchroma×Schroma)+λB，

(1)

其中，Sluma为当前的亮度块与参考块之间的均方差值和，Schroma为当前的色度块与其参考块之间的均方差值和，ωchroma为色度块的加权因子，λ为拉格朗日因子，B为用于CU编码所需的比特数，J为求得的当前CU的率失真代价。

在CU划分过程中，为了确定CU的四叉树结构，需要进行深度从0到3完全遍历，共计算40+41+42+43=85次率失真代价，计算过程较复杂。研究表明，CU划分过程的率失真代价计算占HEVC整个编码时间的40%[8]。因此，在保证视频质量的前提下，提前终止CU的划分，能够降低HEVC的帧间编码复杂度。

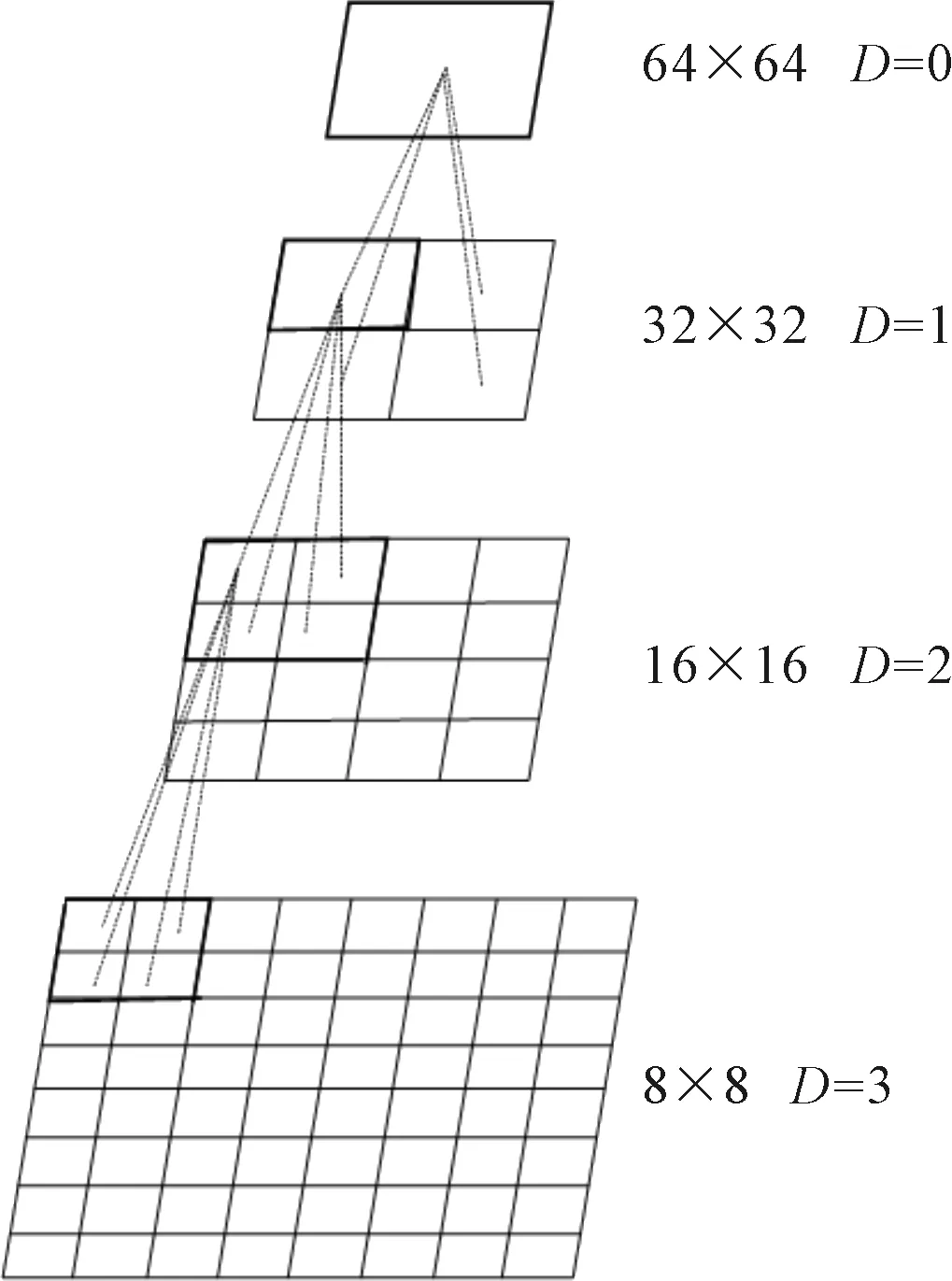
图1 CU四叉树划分图

2 基于CART的帧间CU划分算法

分类回归树[9](classification and regression tree,CART)算法是决策树方法中典型算法之一，该算法选择具有最小的特征属性的基尼系数(Gini index)作为判断能力的度量。本文利用空间相邻CU的深度信息作为CART决策树的判断度量，来实现CU的快速划分。

2.1 CART决策树模型及测试评估

2.1.1 建立CART决策树模型

CU划分问题可归为对不同尺寸CU的划分与不划分二分类问题。设M是对一幅图像进行CU划分的S个数据样本的集合，所包含CU尺寸分别为64×64、32×32和16×16，对应的3个数据样本集合分别Mi(i=1,2,3)。分别将数据样本集合Mi分为划分和不划分2个不同的子类Cij(j=1,2)。当j=1时表示划分；当j=2时表示不划分。在不同尺寸CU进行划分的样本集合Mi中，样本的基尼系数[10]为

(2)

式中pj(j=1,2)表示各个样本中CU被划分与不划分的概率。若Mi中包含的样本数为Si，每个子类Cij中所含的样本数记为Sij，则当前样本的基尼系数可表示为

(3)

采用CART决策树模型需要选择数据样本中最小特征属性的基尼系数作为判断能力的度量[9]。考虑到视频序列是由一系列连续的图像序列组成，相邻视频帧之间有很强的相关性[11-12]。为了统计其相关性，采用表1所示的HEVC标准序列进行深度信息相关性统计，表2为每一帧不同深度下的深度信息统计结果。

表2中的概率为当前CU与相邻CU的深度相关性概率。如表2中59.6%表示当前CU深度为0的情况下，左方LCU中深度为0的CU个数与该LCU下所有CU个数之比值。由表2可看出，相邻CU与当前CU具有同一深度划分的相关性概率较大。因此，将当前CU的左方CU、左上方CU和上方CU的深度信息分别记为Dl、Dl-u、Du，并作为CART决策树模型的特征属性。

在深度信息为Dl的条件下，可把样本Mi分成Ci1,l和Ci2,l两个不同类。Ci1,l和Ci2,l所包含的样本数分别为Si1,l和Si2,l，则在该条件下，集合Mi的基尼系数为

(4)

其中，G(Ci1,l)和G(Ci2,l)分别表示在深度信息Dl情况下，样本集合Mi划分和不划分2个不同子类对应的基尼系数，可依据式(3)计算得到。

依次计算数据样本Mi在Dl-u和Du的情况下对应的基尼系数，以其最小值对应深度信息作为样本Mi的最优特征属性，建立CART决策树模型。

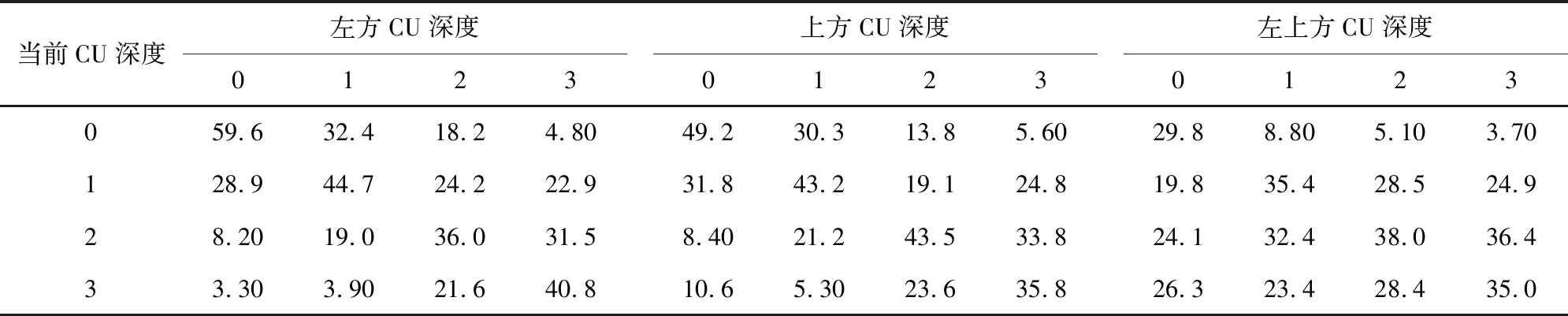
表2 当前CU与相邻CU的深度相关性概率/(%)

2.1.2 CART决策树模型的测试评估

为了测试CART决策树模型对CU划分的准确性，利用HM编码器HM16.0对表1的测试序列CU划分，以评估不同分类器模型对CU的划分性能。实验统计了不同尺寸CU的划分时间和预测准确率，其结果如表3所示。从表中可看出，利用CART模型预测CU划分的时间较短，平均准确率高于90%，适用于编码单元CU的快速划分。

表3 不同尺寸CU的划分时间和预测准确率

2.2 帧间CU的快速编码划分算法

利用CART决策树分类器预测帧间CU的划分结果，其算法可描述如下。

步骤1从CU深度为0开始编码。

步骤2计算当前CU和其最优特征属性的基尼系数。

步骤3判断当前CU的基尼系数。若当前CU的基尼系数小于其最优特征属性的基尼系数，则不划分CU；否则，划分CU。

步骤4对于已划分的CU，判断其深度。若深度小于3，则当前深度加1，且返回步骤2；否则，终止CU划分过程；对于未划分的CU，终止CU划分过程。

3 实验结果及分析

为了验证本文算法的有效性，在HEVC参考软件HM16.0中实现了本文算法。编码器参数为低时延P帧模式，量化参数QP值分别为22、27、32、37,测试帧数为50帧。实验硬件条件为Inter酷睿i5处理器，内存为8GB，采用Windows64位操作系统，运行环境为Microsoft Visual Studio 2010，测试序列如表1所示。

测试中采用通常的评价编码性能参数指标，分别为峰值信噪比的变化Δγ、比特率的变化率ΔRBit和编码时间的变化率ΔT，其定义分别为

Δγ=γ-γHM,

(5)

(6)

(7)

其中：γ、γHM、RBit、RBit,HM和T、THM分别表示本文算法和HM16.0算法峰值信噪比、比特率和编码时间。为了评估本文算法的性能，分别采用了HM16.0算法、文献[6]算法和本文算法的实验测试，结果如表4。

从表4可见，相对于HM16.0，本文算法平均减少43.34%的编码时间，RBit平均增加了1.13%,PSNR平均降低了0.051 dB。与文献[6]算法相比，本文算法能节省10.45%的编码时间，RBit平均降低0.79%，PSNR平均提高了0.021 dB，且本文算法较文献[6]算法降低的0.79%的比特率。主要原因是本文算法比文献[6]算法在CU划分过程中选择了最小基尼系数的特征属性作为CU划分的度量，考虑了最小比特率的限制条件。

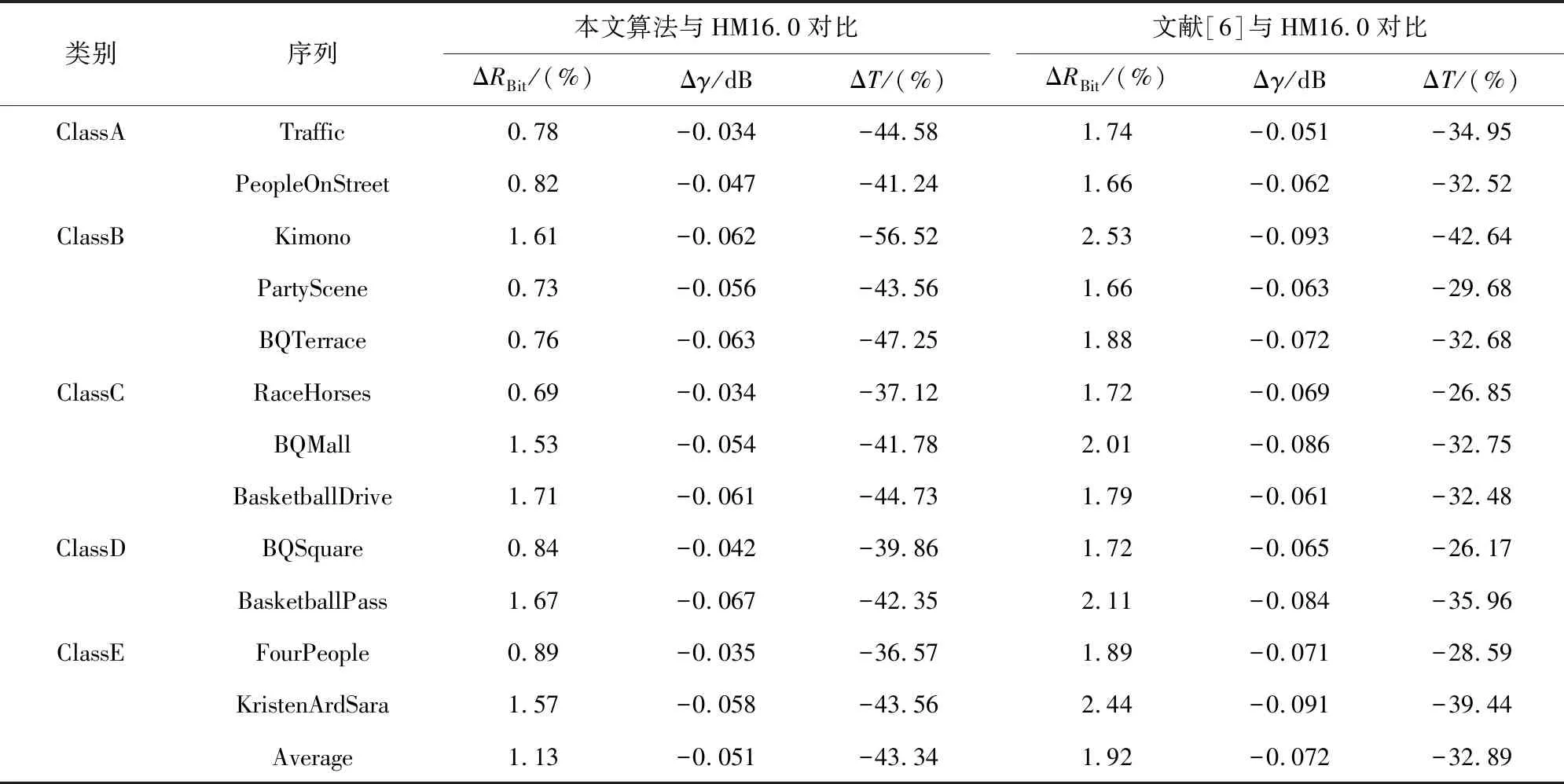
表4 本文算法和文献[6]算法分别与HM16.0算法对比

测试序列采用PeopleOnStreet，在不同QP(22、27、32、37)情况下，分别使用了上述3种算法计算出率失真和编码时间，结果如图2所示。

从图2(a)可以看出，3种算法所得到的率失真曲线基本重合，说明3种编码算法的编码码率和图像质量基本相同。而从图2(b)可以看出，本文算法与HM16.0算法和文献[6]算法相比，编码时间分别减少41.24%和32.52%。可见，本文算法在保持视频质量的同时，有效地提高了HEVC帧间编码的编码效率。

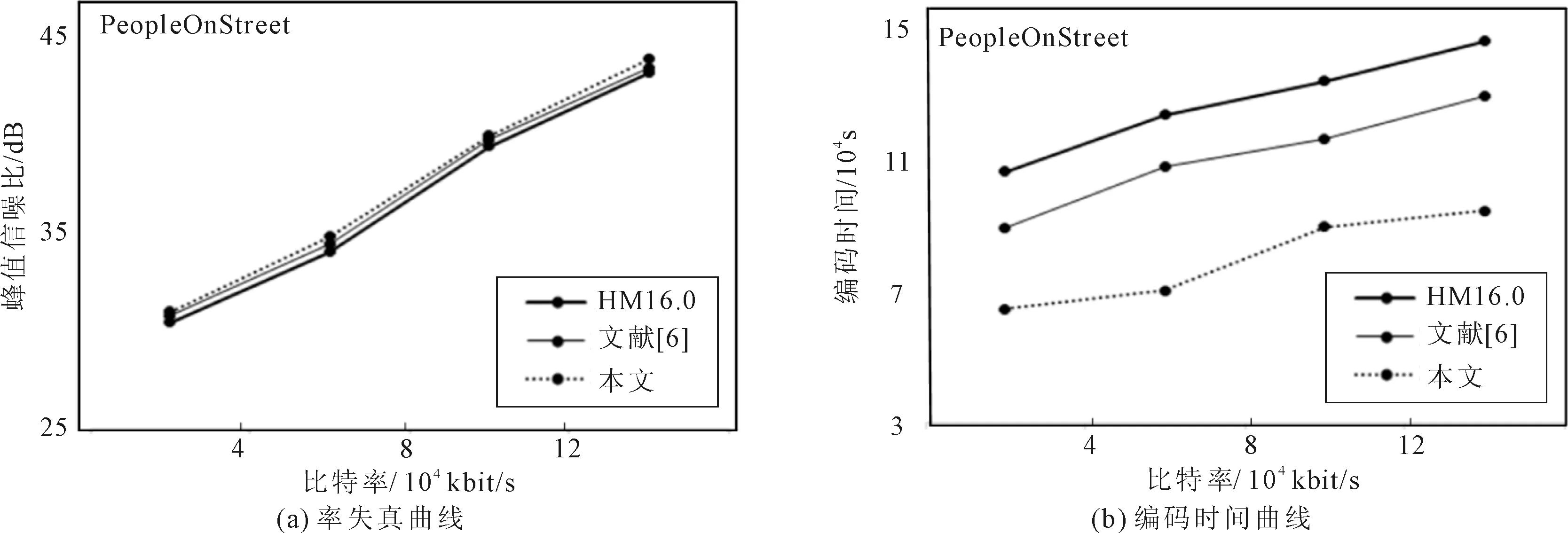
图2 曲线对比

4 结语

针对HEVC的帧间编码过程CU划分复杂度过高的问题，提出了一种基于CART决策树的HEVC帧间CU快速划分算法。算法在CART决策树中利用CU的空间相关性作为判断CU划分的依据，实现对CU的快速划分。实验结果表明，本文算法比HM16.0算法的编码时间平均减少了43.34%，比文献[6]的快速算法还能节省约10.45%的编码时间，有效提高了编码效率。