循环冗余校验串行抵消列表解码算法改进

徐东明, 孙 妍

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

极化码(polar code)是在理论上能达到信道容量的一种编码方式，是5G增强移动宽带(enhance mobile broadband, eMBB)场景的信道编码技术方案[1-4]。串行抵消(successive cancellation, SC)解码算法作为早期的极化码解码算法，纠错性能在无限码长下能够达到信道容量，但对中短码的解码性能较差[5-7]。串行抵消列表(successive cancellation list, SCL)解码算法在SC解码的搜索路径上有了相应扩展，提高了解码性能，但也抬升了计算复杂度[8-10]。目前，性能最佳的极化码解码算法当属有循环冗余校验(cyclic redundancy check, CRC)辅助的串行抵消列表(CRC-SCL)解码算法，它可使极化码解码时在校验性能方面与低密度校验码(low density parity check code, LDPC)相接近[11-13]，其纠错性能更强，但计算复杂度也更高。

考虑到SCL算法同时对L条路径进行搜索解码，这是影响其计算复杂度的主要原因。本文拟通过动态调节L值的大小，并对解码序列进行比特翻转，以此来降低CRC-SCL算法的计算复杂度。

1 极化码解码方案及改进

1.1 极化码解码方案

SC解码是伴随着极化码同时被提出的[4]，其算法以似然比的取值为判决准则，按比特序号从小到大的顺序依次进行解码。当码长N趋于无限长时，由SC解码算法可得无误码的解码比特，且其时间复杂度仅为O(NlogN)。但是，对于中短码，因信道不能完全极化，SC解码会导致部分解码错误。另外，SC解码器在解码过程中依赖于已经解出的信息比特，一旦某解码比特出现错误，势必会影响后续多个解码比特，最终降低解码性能。

在SC解码的搜索路径上进行相应扩展，可得SCL解码算法[8-9]。SCL解码选取路径度量值较大的L条路径，同时对其进行解码搜索，而其他路径则被丢弃[10]。根据解码树按位搜索，若某层路径数小于L，则保留全部路径；若路径数大于L，则保留度量值较大的前L条候选路径，继续下层路径选择，直至解码到最底层；从最底层路径度量值最大的L条路径序列还原发送比特。通常情形下，L值越大，解码误码率越低，但内存使用量也越大。

CRC在信息论和编码空间中被应用于错误检测和纠错[11]。CRC-SCL解码即是在发送比特的信息位中加入CRC码，先进行SCL解码，对保留下的L条路径进行CRC校验，并在通过CRC校验的路径中还原发送比特，从而提高解码算法的纠错能力[12-13]。纠错编码器的输入块由长度为k的信息位和长度为m的CRC校验码组成，后者可看作纠错码源比特的一部分。

1.2 改进后的低复杂度CRC-SCL解码

设计新的解码器，以降低CRC-SCL算法的计算复杂度。

改变SCL解码算法中固定的L值，使其成倍数递增。固定的L值具有一定缺陷：L值定义过小，不能正确还原发送比特；L值定义过大，又会增加算法的计算复杂度。为了解决L值定义过大或过小带来的解码问题，选取动态可调节L值的CRC-SCL解码器。解码器最初采用SC解码，若序列未通过CRC校验，则进行L值为2的SCL解码，若解码一直未成功，迭代地增加L，直至L达到预定义的Lmax值。

将未通过CRC校验的比特位按其似然比排序，选取似然比最小的比特位进行翻转，构成新的序列再次进行CRC校验，校验成功便输出信号，否则执行L扩充解码。

改进后的低复杂度CRC-SCL解码算法流程，可具体描述如下。

步骤1对输入信号序列进行SC解码。

步骤2SC解码完成后，在SC解码保留路径上执行CRC校验。

步骤3如果路径通过CRC校验，则输出该路径，并退出解码，否则转到步骤4。

步骤4先对解码序列进行比特翻转，再进行CRC验证，若通过则输出路径，否则执行步骤5。

步骤5选择L，执行SCL解码，在SCL解码保留路径上执行CRC校验。

步骤6如果有路径通过CRC校验，则输出路径，并退出解码，否则转到步骤8。

步骤7对解码序列进行比特翻转再进行CRC校验，如果该条路径通过CRC校验，则输出路径，否则执行步骤8。

步骤8将L更新为2×L，如果L≤Lmax，则执行步骤5，否则输出路径度量值最大的序列并退出解码。

2 仿真结果

在加性高斯白噪声(additive white Gaussian noise, AWGN)信道，使用含CRC的极化码(1024，512)，仿真信号由二进制相移键控调制(binary phase shift keying, BPSK)调制。考虑到CRC长度对极化码解码性能的影响，采用16位CRC校验码[14-15]。

选取参数N=1 024,k=512,m=16,在不同Eb/No下，各解码算法的误码率如图1所示。SC解码性能远低于CRC-SCL解码性能，改进算法当Lmax=8和Lmax=16时分别与原CRC-SCL算法当L=8和L=16时的解码性能非常接近。

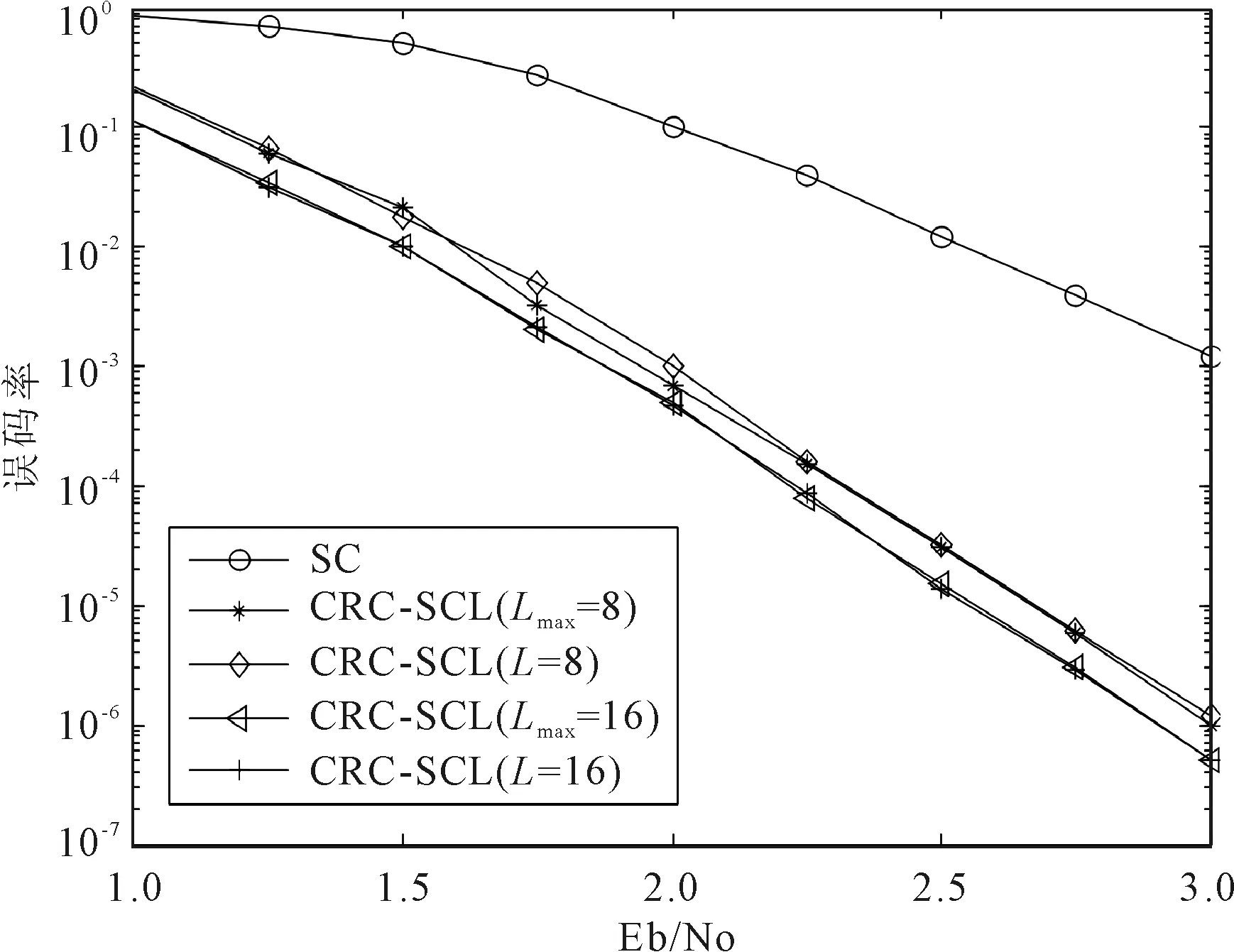
图1 各解码算法的误码率

随着Eb/No增加，改进后的低复杂度CRC-SCL解码器更容易成功解码，且其列表长度的平均值也会变得更小，逐渐趋近于SC解码算法的L值。各算法成功解码的列表长度如图2所示。

(a) Lmax=16

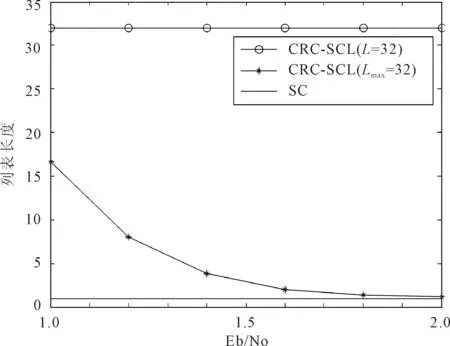
(b) Lmax=32

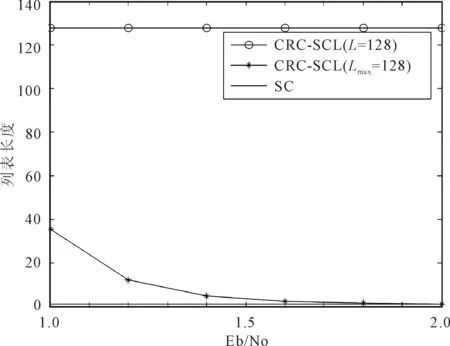
(c) Lmax=128

当Lmax=16，Eb/No=2 dB时，改进后的低复杂度CRC-SCL解码算法虽并不比SC解码算法具有更小计算量，但其成功解码所选列表长度的均值接近于2，相比于L=16对应的SCL解码算法，其计算复杂度还不到后者的1/8。

当Lmax=32，Eb/No=2 dB时，或当Lmax=128，Eb/No=1.8 dB时，改进后的低复杂度CRC-SCL解码算法所选列表长度的均值，已非常接近于SC解码的L值。

所选列表长度越小，算法的计算复杂度越低，故从仿真结果可知，经过改进后的CRC-SCL解码器能够降低解码复杂度，且Eb/No越高，复杂度降低越明显。当Eb/No=1.4 dB时，与原CRC-SCL算法相比，改进算法取Lmax=16时的计算复杂度平均降低62.5%，取Lmax=32时的计算复杂度平均降低87.9%。

3 结语

通过动态调节列表长度以及对序列进行比特翻转，改进CRC-SCL解码算法，可降低其计算复杂度。使用具有16位CRC的极性码(1024,512)进行仿真实验，结果显示，当Lmax=32，Eb/No=2 dB时，或当Lmax=128,Eb/No=1.8 dB时，改进算法的计算复杂度已接近于SC解码算法的计算复杂度。