弧线齿逻辑齿轮设计

盛 伟，冯占荣，王利霞，邹 濛，王文轩

（南昌航空大学 航空制造工程学院，南昌 330063）

0 引言

在机械传动方面，齿轮是常用且重要的零件，随着机械传动对齿轮传动要求的不断提升，促进了不同齿形、不同齿线的齿轮的发展。20世纪80年代后期，日本学者小守勉提出了以全新齿轮理论为基础的逻辑齿轮[1,2]。逻辑齿轮较渐开线齿轮、圆弧齿轮传动的诸多优点：逻辑齿轮的齿廓由许多不同的微线段构成，其采用凹凸齿廓相啮合的形式实现传动，能够有效地解决渐开线齿轮的凸凸啮合形式引发的齿面耐久性差、承载能力低、噪声大等问题，逻辑齿轮可以制成直齿圆柱齿轮，而且还可以制成少齿数齿轮，目前已研制出齿数为3的逻辑齿轮[3,4]。1975年，美国的格里森（Gleason Works）公司首次提出将弧形齿线应用于锥齿轮上，而后国内外众多研究学者展开了对圆弧齿线圆柱齿轮的研究，台湾学者Tseng[5,6]等人用双面刀盘作为展成工具，根据齿条与齿轮的展成啮合理论，建立了渐开线弧线齿圆柱齿轮的数学模型。研究发现弧线齿圆柱齿轮既具有直齿圆柱齿轮的传动特点，又具有斜齿圆柱齿轮的传动特点，还可以克服人字齿齿轮的缺点[7]。将逻辑齿廓与弧线齿齿轮相结合，提出逻辑齿廓弧线齿圆柱齿轮的设计，推导建立齿面数学模型，实现该齿轮的参数化精确建模，以齿轮与齿条的啮合模型代替齿轮与齿轮的啮合模型来探讨该齿轮的重合度及其精确计算方法，并分析了齿宽和圆弧半径对重合的影响，为大重合度的逻辑齿廓弧线齿圆柱齿轮设计提供参考。

1 齿面方程的推导

1.1 逻辑齿轮齿廓线方程

根据文献[3]，逻辑齿轮是由逻辑齿条产形得到的，逻辑齿轮除了与渐开线齿轮共有的参数外，还有初始基圆半径G0、初始压力角α0、相对压力角δ等参数。图1为逻辑齿条齿廓线，式(1)为单侧齿廓线AB的方程，其中正号表示节线以上的齿廓线AO1的方程，负号表示节线以下的齿廓线O1B的方程，式(2)～式(6)为逻辑齿轮基本参数的计算公式，由齿轮啮合原理[8]可推导逻辑齿轮齿廓线方程，如式(7)所示。

图1 逻辑齿条的齿形

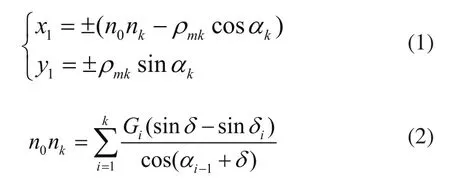
1.2 弧线齿逻辑齿轮齿面方程

图2为弧线齿齿轮坐标系及分度圆柱面展开图，建立坐标系ohxhyhzh和坐标系os-xsyszs，zh与zs同向，平面xhohyh和平面xsosys相距h，xh轴和xs轴相比，绕zh轴或zs转动了β角。其中B为齿宽，L为圆弧齿线，RT为圆弧齿线的半径，R为分度圆半径。

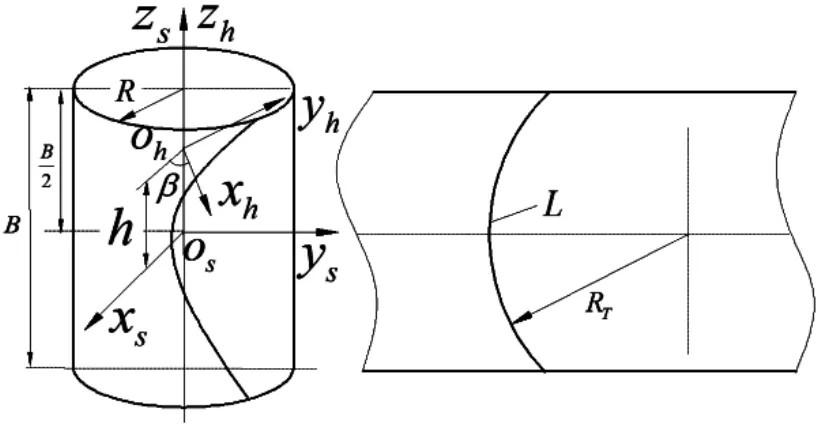
图2 弧线齿齿轮坐标系的设定

逻辑齿轮的齿廓线在坐标系xhohyh中的方程。

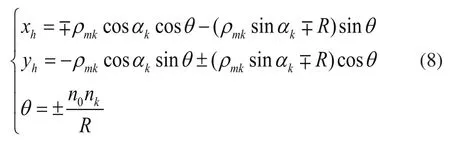
根据弧线齿圆柱齿轮的几何关系，弧线齿的位置角为：

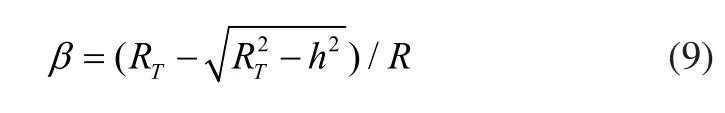
根据坐标变换，在坐标系os-xsyszs中的逻辑齿廓弧线齿圆柱齿轮齿面方程为式(10)，其中正负号分别表示单齿一侧的分度圆以内、分度圆以外的齿面方程。

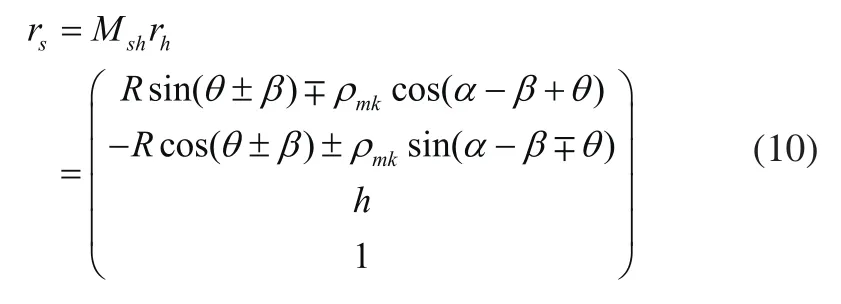
2 参数化建模

根据弧线齿逻辑齿轮的齿面方程推导过程，通过MATLAB数值计算和CATIA三维建模功能实现弧线齿逻辑齿轮参数化建模，具体步骤如下：

1）根据逻辑直齿齿轮的齿槽方程编写齿槽点集（x,y坐标）。

2）然后给定齿线的圆弧半径（或齿宽），然后依据圆弧半径一般为齿宽的0.6～4倍，确定齿宽值（或圆弧半径）。

3）沿齿宽方向将轮齿齿槽等分，取zs=hi（i=1，2，…，n），zs的每次取值，都会得到一条齿槽廓线的点集。

4）将n条廓线的点集以如下程序区分开，即每一个“EndCurve”和“StartCurve”之间为一条曲线的点集。“EndCurve”和“StartCurve”是CATIA软件中自带宏程序表格中的一条曲线的点集“起始”和“终止”的标志。

5）将保存在.txt文档中的点坐标直接复制粘贴到CATIA软件中自带宏程序的表格中并运行宏，得到齿面点集及齿槽廓线，进而拟合成单侧齿槽面。

6）变换方程，重复步骤2）～5），便可得到一个完整的齿槽面。

7）阵列齿槽面并作曲面切割毛坯实体得到弧线齿逻辑齿轮精确三维模型。

在MATLAB、CATIA中，由步骤1）～7）可得到弧线齿逻辑齿轮模型，参数建模方法的齿面形成过程如图3所示。

3 重合度的研究

3.1 重合度的计算方法

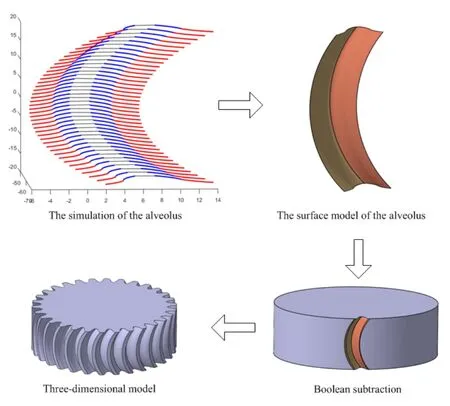
图3 参数化建模过程

重合度是衡量齿轮承载能力与传动平稳性的重要指标。渐开线齿轮的重合度可表述为啮合线长度与基圆齿距的比值，该定义对于逻辑齿轮显然是不适用的，因为逻辑齿轮并没有确定的基圆。陈安适[9]将逻辑直齿轮的重合度定义为节圆上的啮合弧长与相邻两齿同侧齿廓在分度圆上的弧长比值，但没给出啮合弧长的计算公式。而弧齿圆柱齿轮副的重合度ε等于轴向重合度与端面重合度的和。弧线齿圆柱齿轮的轴向重合度计算公式是：

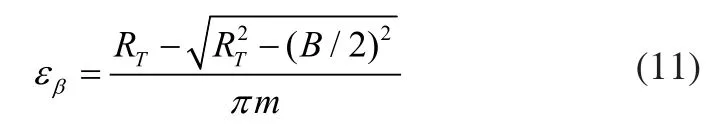
逻辑齿廓弧齿圆柱齿轮的端面重合度可以按逻辑直齿圆柱齿轮计算。根据式(1)可知，逻辑齿条的单侧齿廓线的节线以上部分（AO1）与节线以下部分（O1B）关于原点对称，所以这两段的啮合弧长相等。那么，端面重合度的计算公式如下：

首先分析逻辑齿条的齿廓AO1与逻辑齿轮传动时的啮合轨迹线。根据齿轮啮合原理[8]，齿轮齿条传动时，齿轮的节圆与齿条的节线以纯滚动的形式啮合传动，如图4所示。

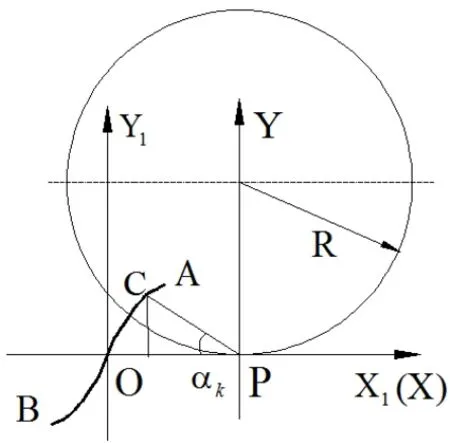
图4 齿轮—齿条啮合示意图

那么P点既是齿轮与齿条的相对瞬心，又是齿轮齿条传动时的节点。根据齿轮啮合原理[8]，两齿廓啮合时，其啮合点的公法线必然经过P点。图中坐标系X1OY1是齿条的动坐标系，XOY为齿条的静坐标系，那么啮合点C在坐标系XOY中的坐标是：

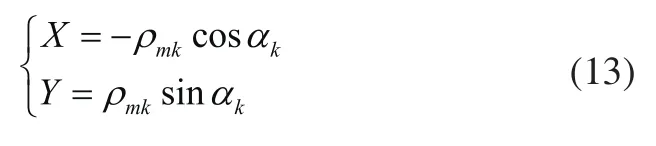
利用式(13)即可通过MATLAB软件求出所有啮合点的坐标，然后将得到的点集导入CATIA自带宏程序的EXCEL表格中，在CATIA中自动生成点以及由一系列点构成的曲线，即啮合轨迹线。同理可计算出逻辑齿条的单侧齿廓线的节线以下部分与逻辑齿轮传动时的啮合轨迹线。两段啮合线的弧长b可直接在CATIA软件的草图界面使用测量项直接得到精确的值，如图5所示。

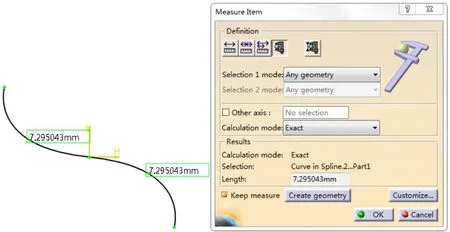
图5 啮合弧长的测量

3.2 重合度的影响因素

为分析齿宽和圆弧半径对逻辑齿廓弧线齿圆柱齿轮重合度的影响，取逻辑齿轮基本参数如表1所示。齿宽和圆弧半径对重合度的影响如图6、图7所示。

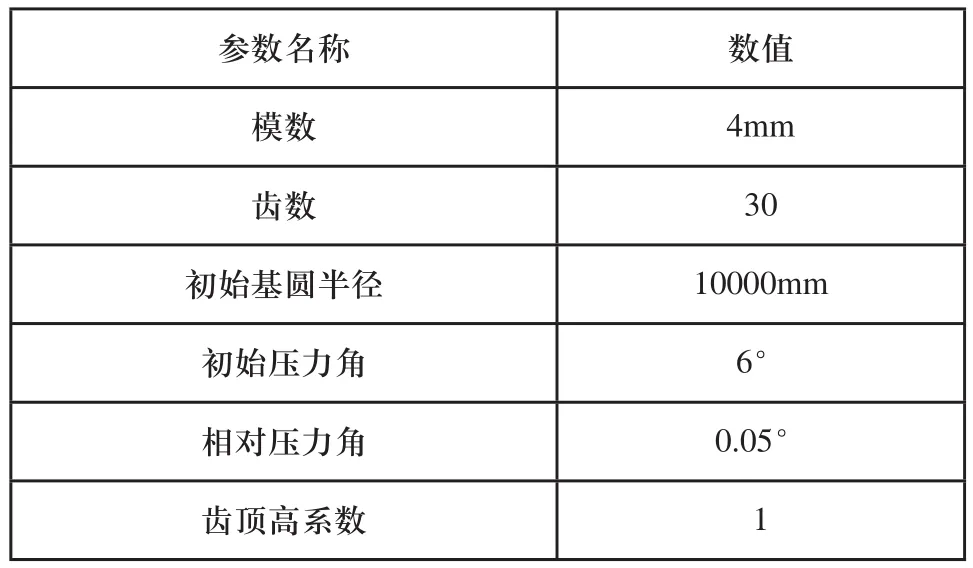
表1 逻辑齿轮基本参数

当保持齿宽不变时，适当的减小圆弧半径；当保持圆弧半径不变时，有利于增大该齿轮的重合度。

4 结论

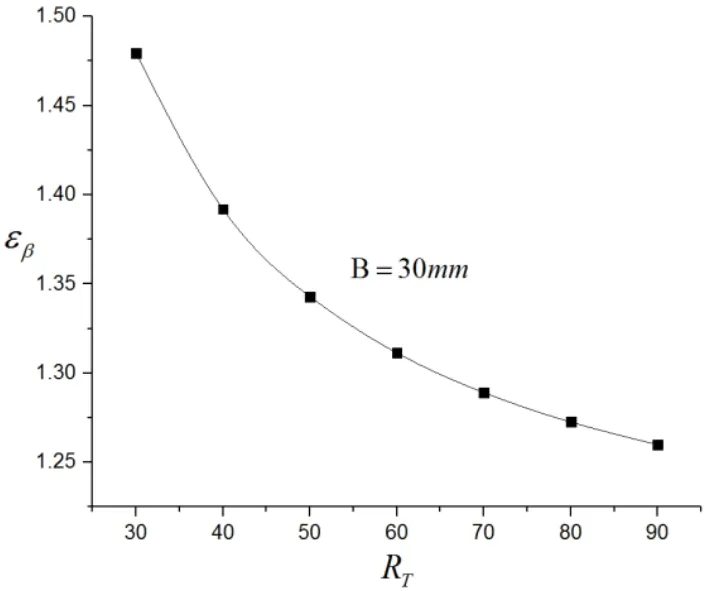
图6 圆弧半径对重合度的影响

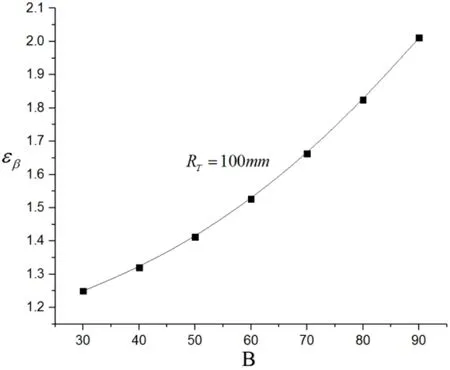
图7 齿宽对重合度的影响

本文提出逻辑齿廓弧线齿圆柱齿轮设计，根据齿轮啮合原理，推导建立了该齿轮的数学模型，利用MATLAB软件和CATIA软件实现该齿轮的参数化建模。以齿轮——齿条模型代替齿轮——齿轮啮合模型，提出精确分析和计算该齿轮的重合度的方法。在此基础上，分析了齿宽和圆弧半径对该齿轮重合度的影响，研究表明：增大齿宽或减小圆弧半径有利于增大弧线齿逻辑齿轮的重合度。这为设计大重合度的逻辑齿廓弧线齿圆柱齿轮提供理论参考。