一种用于密度法的SR插值模型

刘晓晨，孙 宇 ，敬石开，郄龙飞

（1.南京理工大学 机械工程学院，南京 210094；2.北京理工大学 机械与车辆学院，北京 100029）

0 引言

拓扑优化是一种在给定设计区域内，根据边界及载荷条件，在满足特定限制要求的情况下实现结构性能最优的先进设计方法，其属于结构优化设计的一种[1]。自1988年Bendsoe和Kikuchi[2]提出均匀化方法以来，拓扑优化得到快速发展，目前已发展出多种类型的优化方法，如密度法[3]、水平集法[4]、渐进结构法[5]、组件优化法[6]、拓扑导数法[7]等。

密度法是常用的一种拓扑优化方法，其基本思想是人为的引入一种假想的取值为{0,1}的密度变量，其中0代表空相材料，由白色表示，1代表实体相材料，由黑色表示。建立拓扑优化模型时，以材料密度为设计变量，通过单元密度值来控制单元的增删，实现拓扑结构的改变。

因设计变量只能取值0或1，上述拓扑优化问题是一个典型的离散变量拓扑优化问题。离散变量拓扑优化问题是指设计变量在优化过程中只能取某些离散值，而不是在一个区间内连续变化[8]。因设计变量不连续，导致目标函数和约束条件不可微，因此离散变量拓扑优化问题在求解时只能借助组合数学方法，而不能使用解析数学方法[9]。但拓扑优化的典型特征就是设计变量规模大，密度法中设计变量数量与有限元网格划分数量相等，均匀化方法中设计变量数量是有限元网格划分数量的3倍。这带来的问题就是“组合爆炸”，某些情况即使借助计算机也难以求解。

为了避免离散变量拓扑优化中的上述问题，通常对设计变量进行松弛，将设计变量取值范围由{0,1}放松到[0,1]，允许其在0到1之间连续取值。此举有效缓解了优化求解过程中的组合爆炸问题，但是将密度值松弛到[0,1]意味着在优化过程中引入了中间密度变量（即处于0和1之间的密度变量），中间密度变量没有物理意义，并且使得优化结果中产生大量的灰度单元（介于黑与白之间的灰色单元）。

为了抑制中间密度单元的产生，密度法中通常采用惩罚策略对中间密度变量进行处理，迫使其向0或者1两端靠拢，从而得到清晰的0-1解，此类方法又称为材料插值模型。密度法中最有代表性的材料插值模型是SIMP模型[10,11]和RAMP模型[12]。SIMP模型通过幂指数的形式对中间密度单元进行惩罚，RAMP模型通过有理数的形式对中间密度单元进行惩罚，其与SIMP模型的主要区别是设计变量在0处的敏度不为0，这有助于抑制低密度值单元的产生，并提高优化过程稳定性。但RAMP模型采用有理数的形式进行惩罚，其优化效率远低于SIMP模型。

总的来说，SIMP模型具有较高的优化效率，RAMP模型具有较高的稳定性。但二者仍处于割裂状态，为了充分利用二者的优势，可以构建统一的惩罚模型。统一模型一般采用加权的形式，这种处理方式在多相材料中已有出现[13]：对于没有空白相的两相材料结构，可以使用插值，该插值对于每个材料相采用Hashin-Shtrikman上限和下限的加权平均值方式进行处理；对于带有空白相的两相材料结构，则使用SIMP模型和Hashin-Shtrikman模型进行混合插值处理[14]。

受此启发，本文首先提出一种SIMP模型和RAMP模型加权的插值模型，即SR模型。SR模型通过加权因子将SIMP和RAMP向结合，通过调整加权因子的取值，SR模型可以转换为SIMP模型或者RAMP模型；其次，在SR模型框架下，构建了以机械柔顺度为目标函数，体积约束为约束条件的拓扑优化模型；最后，研究了适用于该优化模型的优化准则求解算法，以及SR模型在不同加权因子取值策略下的惩罚效果。

1 SR模型构建基础

SIMP模型和RAMP模型均属于隐式惩罚法，其直接对设计变量进行惩罚。SIMP模型采用幂指数的形式对中间密度单元进行惩罚，单元i的杨氏模量Ei可表示为：

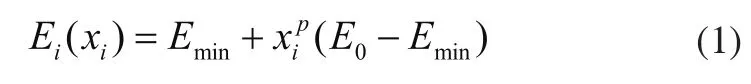
其中，E0表示固体相的杨氏模量，Emin表示空白相的杨氏模量，其被赋予一个非常小的值以防止优化过程中刚度矩阵变得奇异，xi为设计变量密度，p为惩罚因子。图1展示了惩罚因子p在不同取值下的SIMP插值模型的变化曲线。

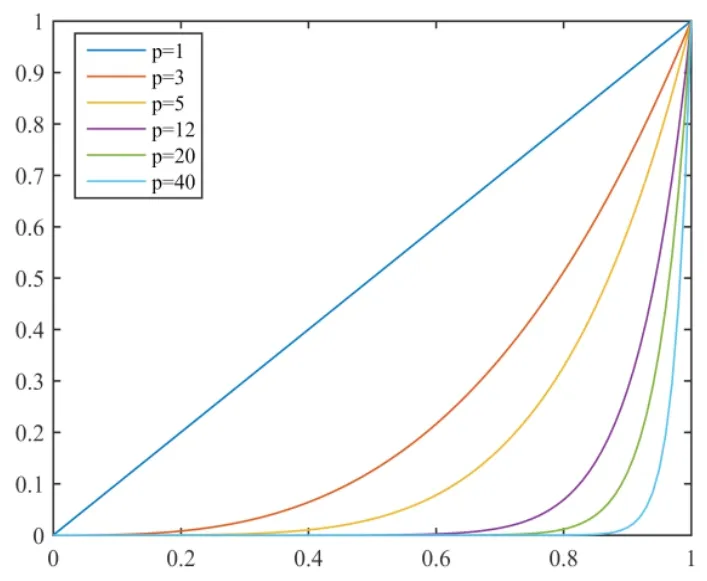
图1 SIMP插值模型曲线图

图1中X坐标为设计变量密度，Y坐标为单元杨氏模量。如图所示，当惩罚因子p取值为1时，SIMP模型为一条直线，此时SIMP模型对中间密度单元没有惩罚力度，目标函数为凸函数，优化模型有唯一的全局最优解；随着惩罚因子p取值增加，SIMP模型对中间密度单元的惩罚力度逐渐加强，目标函数由凸函数转为非凸函数。从图1中可以看出，当惩罚因子p取值大于20时，密度值处于0.8以下的单元基本被归为0。

RAMP模型采用有理数的形式对中间密度单元进行惩罚，单元i的杨氏模量Ei可表示为：

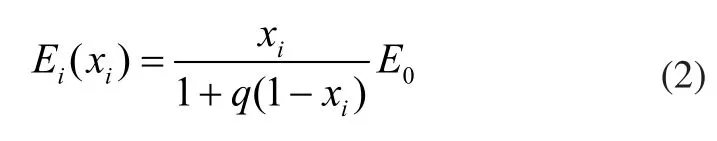
其中，q为惩罚因子。图2展示了惩罚因子取值相同时，SIMP模型和RAMP模型惩罚力度的对比情况。

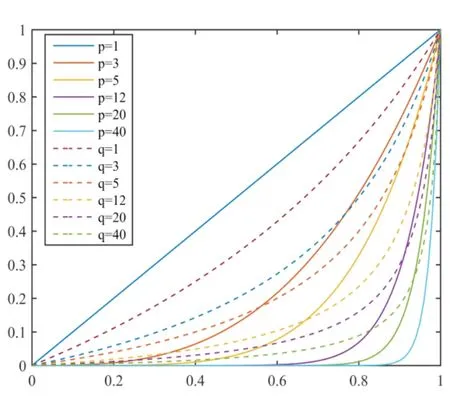
图2 SIMP模型和RAMP模型对比图

图2中X坐标为设计变量密度，Y坐标为单元杨氏模量。SIMP模型惩罚曲线由实线表示，RAMP模型惩罚曲线由虚线表示。区别于SIMP模型，当惩罚因子取值为1时，RAMP模型对中间密度单元有惩罚力度，对于其他惩罚因子取值，RAMP模型的惩罚力度均低于SIMP模型。

2 SR模型构建

假设最优拓扑构型由Ωs表示，由密度法的定义可知，Ωs是设计域Ω的子域，在Ωs上设计变量数值为1，在Ω/Ωs区域设计变量值为0。如果用E1和E2分别表示两种材料的杨氏模量，则第i个单元的杨氏模量需要满足：

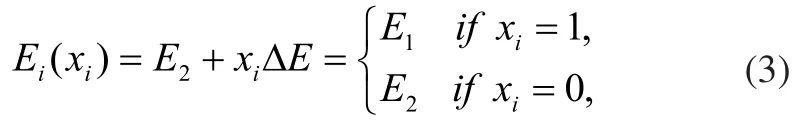
其中，ΔE=E1-E2。式(3)中，假设材料1的泊松比与材料2的泊松比相同。在密度法中，固体相被视为材料E1，空白相被视为材料E2，则插值模型需满足：

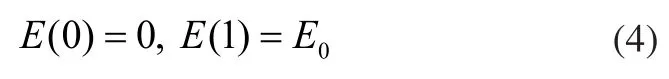
基于此，SR模型中杨氏模量和设计变量的关系式为：

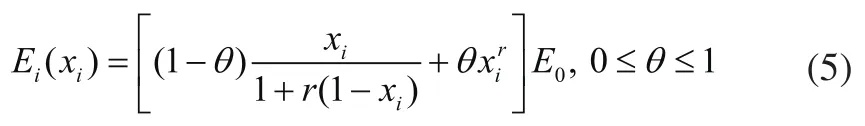
其中，r为惩罚因子，θ为加权因子。加权因子θ决定SR模型中SIMP模型和RAMP模型的权重：当θ=0时，SR模型转化为RAMP模型；当θ=1时，SR模型转化为SIMP模型。

图3展示了惩罚因子r取值为5时的SR模型的插值曲面图。

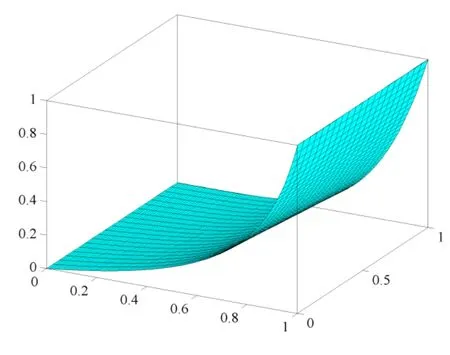
图3 SR插值模型曲面图

图3中，X坐标为设计变量，Y坐标为加权因子，Z坐标为杨氏模量，惩罚因子r取值为5。当惩罚因子取不同数值时，区别于SIMP模型和RAMP模型的曲线图，SR模型为一系列不同的曲面。如上所述，当惩罚因子取值为0时，SR模型转化为RAMP模型；当惩罚因子取值为0时，SR模型转化为SIMP模型。在图3中，θ=0时SR模型的曲线与RAMP模型中q=5的曲线相同；θ=1时SR模型的曲线与SIMP模型中p=5的曲线相同。因此，r=5的SR模型曲面为q=5的RAMP模型过渡到p=5的SIMP模型所形成。

3 基于SR模型的拓扑优化模型

对于以机械柔顺度为目标函数，体积约束为约束条件，采用SR插值模型的拓扑优化模型可表示为：

其中，c=UTKU为目标函数机械柔顺度，K，U和F为别表示全局刚度矩阵、全局位移矩阵和全局载荷矩阵，ui表示单元i的位移，ki为单元刚度矩阵，k0表示单位杨氏模量的单元刚度矩阵，G0为体积约束，V表示优化后设计域的体积，V0表示原始设计域的体积，vi表示单元i的体积，n表示有限元网格划分的数量，xmin为一很小的正数，为了避免优化过程整体刚度矩阵变得奇异。

4 SR拓扑优化模型求解

根据OC算法的原理[15]，用于求解SR拓扑优化模型的优化准则算法可以通过优化模型中目标函数和约束条件所构建的拉格朗日函数进行推导。公式(6)对应拓扑优化问题的拉格朗日函数为：

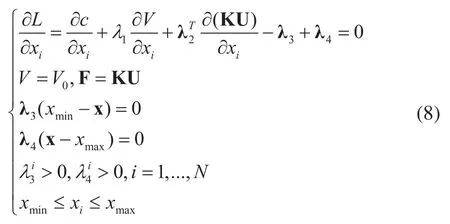
当xi=xmin时，设计变量上限无效，此时；当xi=xmax时，设计变量下限无效，此时；当时，设计变量的上下限均无效，此时。基于此，式(8)可转变为：

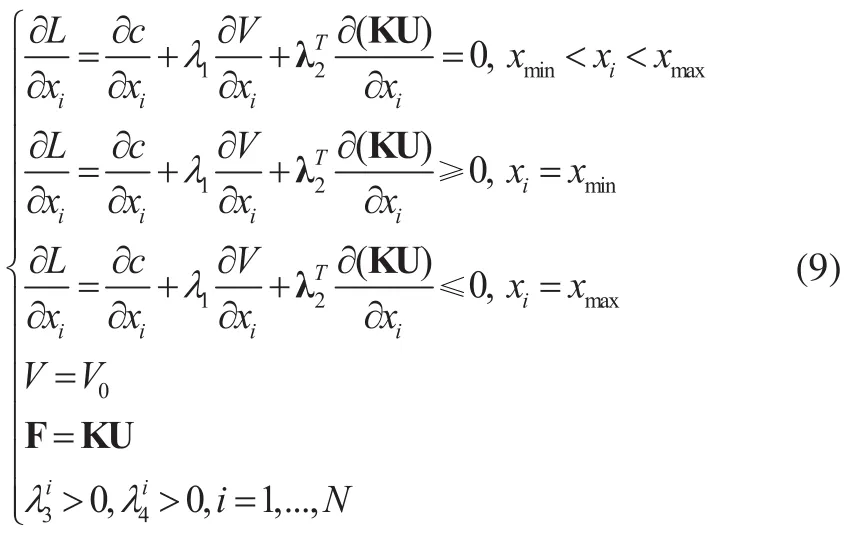
将机械柔顺度c=UTKU代入式(9)，考虑等式项，可得：

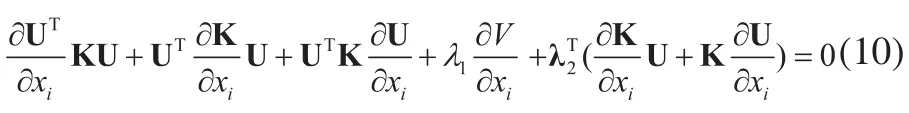
在SR模型中，单元刚度矩阵ki和单位杨氏模量刚度矩阵k0关系为：

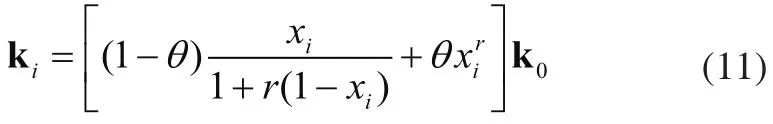
将其代入式(10)，并结合整体刚度矩阵的对称性，可得：

OC算法的优化设计准则表示为：

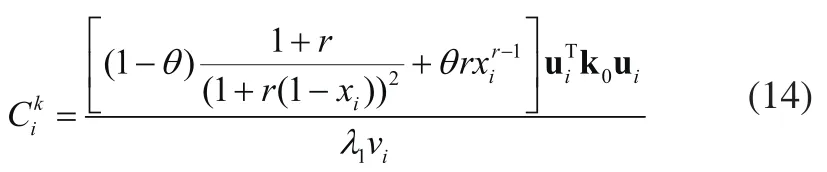
将设计变量的上下限代入式(14)中，可得OC算法的迭代优化公式：

其中，引入阻尼系数η以保证优化过程的稳定性和收敛性。一般地，当满足以下条件时，OC算法停止迭代：

其中，ε为任意小的正数。

5 数值算例

本节以MBB梁为对象测试SR模型在不同惩罚因子取值策略下的优化效果。采用敏度过滤器进行过滤。MBB梁的设计域、边界条件及载荷情况如图4所示（由于对称性，图中仅展示一半MBB梁），其左端面为对称结构，左上角作用一个大小为1，垂直向下的力F，右下角处为水平支撑，设计域的长宽比例为3:1。参数设置如下：网格划分120×40，体积分数取值为0.5，惩罚因子取值为4，过滤半径取值为4。

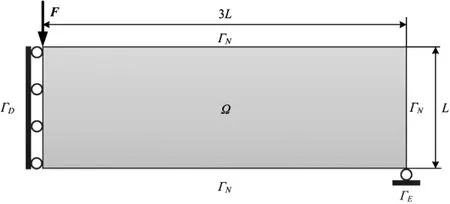
图4 MBB梁的设计域、边界条件及载荷情况

为了评价优化结果的0/1离散率，本节引入指标Mnd指标[16]，其表达式为：

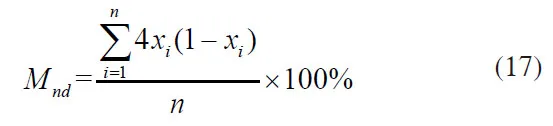
图5展示的是SIMP模型和RAMP模型的优化结果。

图5 MBB梁的优化结果

图5(a)为SIMP模型优化结果，其右上部分和左下部分支撑处出现明显的灰度单元聚集区域。RAMP模型的优化结果较为清晰。两者的优化结果中均未出现棋盘格和网格依赖问题。

图6展示的SR模型θ取值为0.25，0.5和0.75的优化结果。

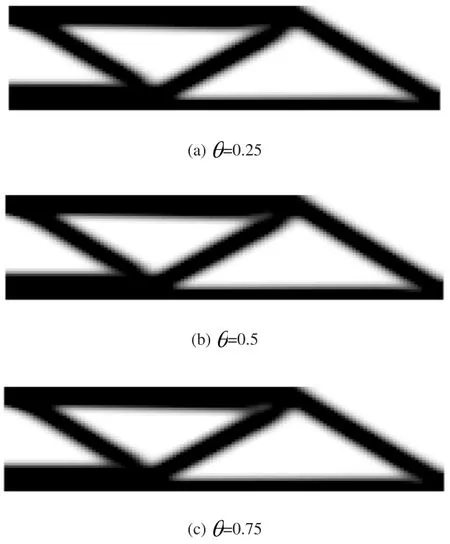
图6 MBB梁的优化结果

由图6可以看出，SR模型的优化结果中在上下两支撑处未出现明显的灰度单元聚集区域，并且在非支撑区域也存在较少中间密度单元，优化结果清晰，没有产生网格依赖和棋盘格现象。上述测试的优化数据如表1所示。

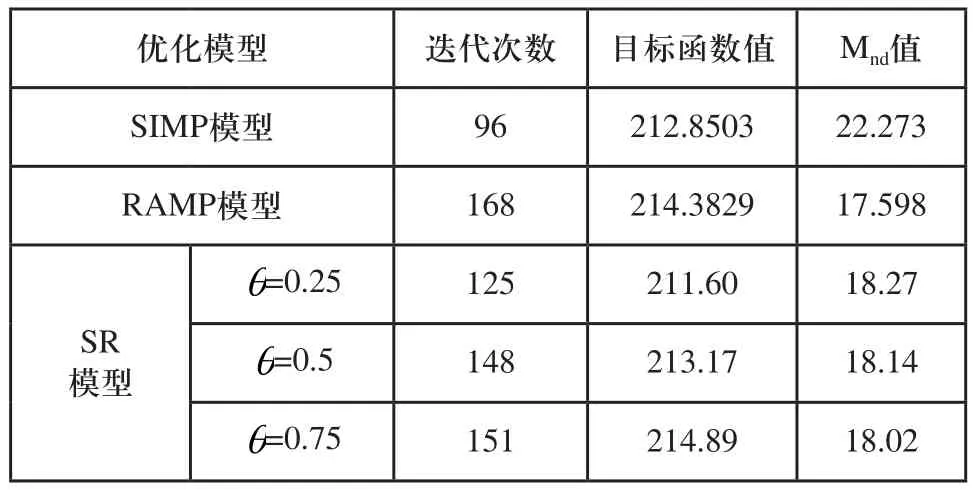
表1 MBB梁优化数据

SIMP模型采用幂指数的惩罚形式，相同参数下，其收敛速度最快，迭代次数最少。当θ取值为0.25时，SR模型体现出SIMP模型的特征，具有较快的收敛速度，且目标函数值和Mnd值均低于SIMP优化结果。随着加权因子取值增大，SR模型迭代次数不断增加。其原因是SR模型逐渐由SIMP模型过渡到RAMP模型，其惩罚效率逐渐降低。三种加权因子取值下SR模型优的迭代次数均低于RAMP模型的迭代次数。

目标函数值也体现出同样的规律：SR模型θ=0.25优化结果的目标函数值最低，目标函数值随着加权因子取值增大而增大。需要指出的是，θ=0.25时SR模型目标函数值低于SIMP模型，θ=0.75时目标函数值高于RAMP模型，这是SR模型与SIMP和RAMP模型的差异。

0-1离散率方面，SIMP模型因其优化结果中上下两支撑处产生灰度单元聚集区域，其Mnd值较高。SR模型和RAMP模型的Mnd值明显低于SIMP模型Mnd值。加权因子取越大值时，SR模型优化结果的Mnd值越低。

6 结论

密度法中通过对设计变量进行松弛来避免离散变量拓扑优化问题求解时的组合爆炸问题，为了抑制因松弛操作而引入的中间密度单元，密度法中通常引入材料插值模型，对中间密度单元进行惩罚，使其向0或1两端靠拢。

本文首先提出一种SIMP模型和RAMP模型的加权材料插值模型，即SR模型。该模型通过引入加权因子将SIMP与RAMP相结合，通过调整加权因子的取值，SR模型可转化为SIMP模型或者RAMP模型。基于此，本文分析了SR模型的惩罚曲面特征，并构建了以机械柔顺度为目标函数，体积约束为约束条件，采用SR插值模型的拓扑优化模型；其次，研究了适用于该模型的优化准则求解算法。以MBB梁为例，验证SIMP模型、RAMP模型以及SR模型的优化特征，研究加权因子对优化结果的影响关系。

实验表明，SR模型可获得较为清晰的优化构型，优化结果中无棋盘格和网格依赖现象，并且没产生明显的中间密度单元聚集区域。通过调整加权因子取值，SR模型表现出SIMP模型收敛速度快以及RAMP稳定性高的特点；通过分配较大的惩罚因子，SR模型可获得低Mnd值的优化结果，并且优化过程没有出现震荡。