基于XFEM的平板斜裂纹动态扩展数值模拟*

彭 英 杨 平 柯叶君

(武汉理工大学交通学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063) (华中科技大学土木工程与力学学院3) 武汉 430074)

0 引 言

在极端恶劣海况，以及碰撞、地震等突发事件中，船舶与海洋结构物所承受的环境载荷必须按动态载荷处理.当含裂纹的结构受到动态载荷作用时，由于材料的惯性，载荷以应力波的形式传播，而应力波与裂纹的相互作用使得动态比准静态断裂问题复杂得多，因此，研究裂纹在动态载荷下的起裂、扩展和止裂是一项极具意义及挑战性的工作.

目前用于模拟裂纹扩展的方法主要有传统有限元法+自适应网格[1]、虚拟裂纹闭合技术(VCCT)[2]、节点力释放方法[3]、单元间内聚力模型[4]等.而这些方法都具有一定的局限性，比如，伴随裂纹扩展必须不断进行网格重构、裂纹扩展路径必须预先给定、裂纹只能沿着单元边界扩展、计算成本偏高等.为了更好的解决这些问题，Belytschko等[5]提出单位分解扩充法， Moёs等[6]随后引入阶跃函数和裂尖函数两种扩充形函数分别对裂纹面和裂尖进行描述，并称之为“扩展有限单元法”(XFEM)，继而Sukumar等[7]又将其延伸至三维裂纹问题.由于XFEM在计算过程中对不连续场的描述可以完全独立于网格边界，因此，应用XFEM模拟裂纹扩展时，无需进行网格重构，并可模拟裂纹沿任意路径扩展.但是，以往有关裂纹扩展方面的研究大多局限于准静态问题[8-9]，而对于冲击载荷下裂纹动态扩展的研究，由于问题的复杂性，相关文献还十分少见.

文中基于XFEM，采用有限元软件ABAQUS对含斜裂纹矩形板的冲击破坏过程进行了系列数值模拟研究，并讨论了裂纹初始角度、裂纹长度和冲击载荷形式等参数对裂纹扩展路径的影响，得到平板斜裂纹动态扩展的一些规律.

1 基本理论

扩展有限元法(XFEM)的基础是单位分解，通过对标准近似场添加阶跃函数和裂尖函数两种扩充形函数以对未知场进行更精确的描述，见图1a).由于这种混合增强不易并入瞬态解法中，因此，在动态应用中为避免裂尖增强，使裂尖只在单元边界之间移动，即每次裂纹扩展都会贯穿整个单元，从而可以只采用阶跃增强函数描述不连续场，见图1b)，其位移场uh(x)为[10]

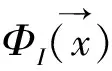
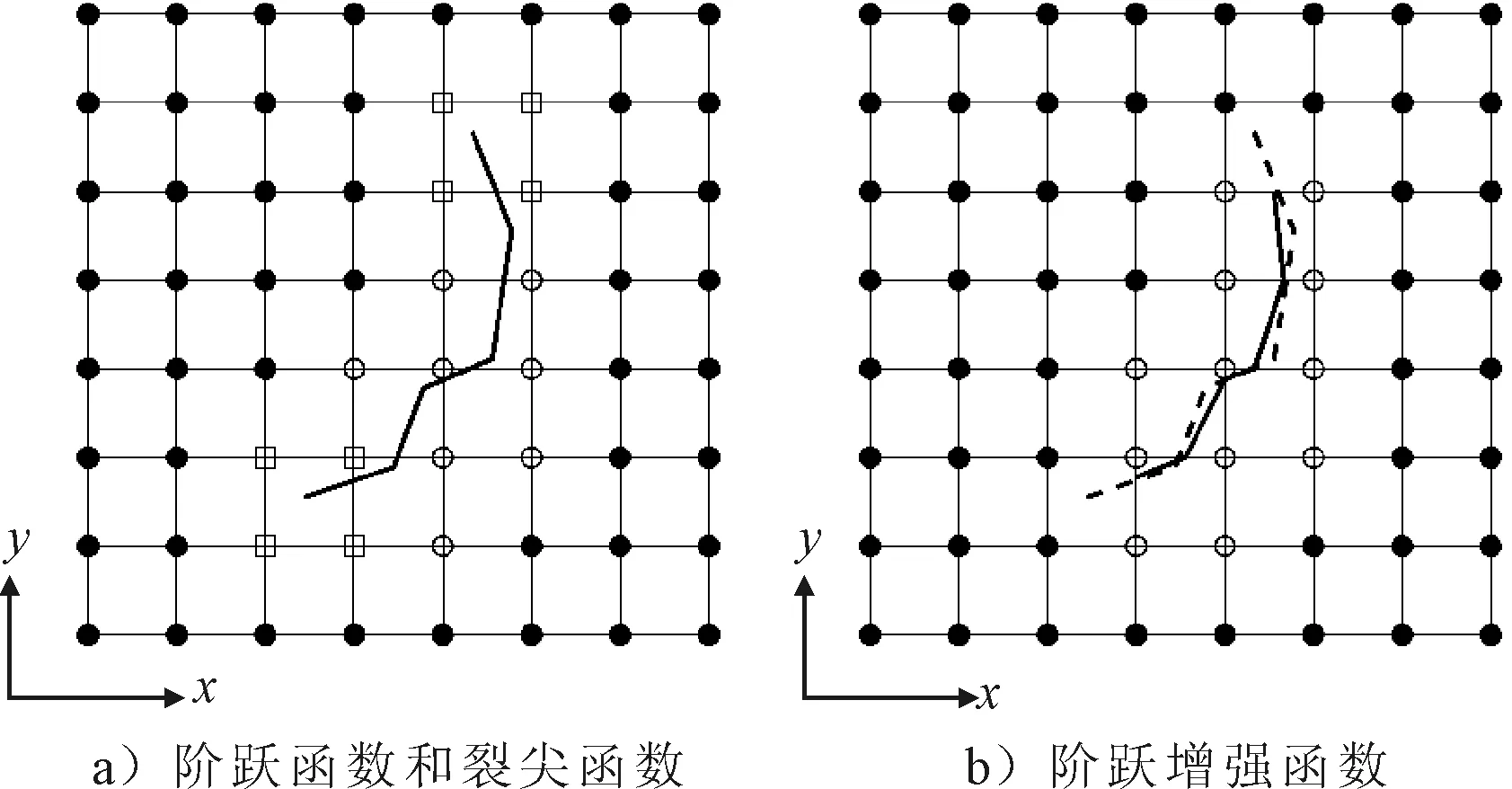
图1 二维裂纹中节点扩充方案

2 计算模型

计算模型见图2，在左边缘中心位置有一条初始斜裂纹，矩形板宽度2W=100 mm、长度2H=160 mm、厚tp=3 mm，初始裂纹长度a=20 mm，裂纹倾角θ=45°.矩形板材料均匀、各向同性、线弹性，弹性模量E=206 GPa，泊松比ν=0.3，密度ρ=7 800 kg/m3，最大主应力为100 MPa.矩形板底端固定，顶端受到拉伸阶跃载荷p(t)作用，载荷峰值p(0)=80 MPa，持续时间t=50 μs.

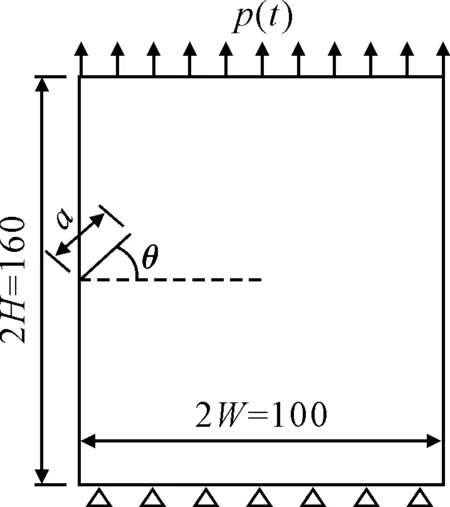
图2 斜裂纹矩形板几何模型

在ABAQUS软件中，XFEM计算动态裂纹扩展时并未引入裂尖增强函数，每次裂纹扩展都会贯穿整个单元，为避免因单个时间增量步裂纹扩展距离过大而导致计算误差，对裂纹可能的扩展区域进行局部网格细化，网格尺寸取为1 mm，见图3.本文采用四节点四边形平面应力单元(CPS4)，裂纹面间的接触行为采用切向无摩擦、法向“硬接触”，采用牵引分离损伤法(damage for traction separation laws)的最大主应力断裂准则(maxps damage)，并且采取自动时间步长求解，最大时间步长取为0.5 μs.由于裂纹扩展问题属于强间断、强非线性问题，为了提高求解过程的收敛性，取黏性系数为5×10-5，并且增大迭代计算中允许的尝试步数和每步允许的迭代次数.此外，在模型输出定义中需要选定裂纹面水平集函数(PHILSM)及裂纹扩展状态参量(STATUSXFEM)，以在后处理中可以显示裂纹位置和扩展情况.

图3 有限元网格模型图

图4给出了平板内斜裂纹的扩展过程，图中的应力云图为Von Mises应力. 由图4可见，当矩形板顶端受冲击载荷作用后，应力波从顶端逐渐向下端传播，当时间t=14.247 μs时，裂纹开始扩展，起初裂纹扩展较慢，几个时间步长裂纹才能向前扩展一个单元，长度约为1 mm；当时间t=32.770 μs时，应力波到达底端并发生反射，此后，在应力波与反射波的共同作用下，裂纹扩展速度明显加快；当时间t=49.056 μs时，裂纹横向贯穿整个矩形板.

图4 平板内斜裂纹的扩展过程图

3 不同影响参数下的裂纹扩展路径对比

3.1 裂纹初始角度的影响

针对图2中的计算模型，分别取裂纹倾角θ=15°,45°,75°，其他参数保持不变，采用XFEM计算不同初始角度下的裂纹扩展路径，裂纹扩展过程中的单元状态见图5.由图5可知，裂纹扩展过程中，路径会发生微小波动，但基本是按Ⅰ型裂纹形式沿直线扩展，说明裂纹的初始角度影响不大，不能决定裂纹的扩展路径.表1为不同初始角度下，裂纹开始扩展的时间(t1)、横向贯穿矩形板的时间(t2)和贯穿矩形板的时间间隔(Δt).由表1可知，裂纹初始角度越小，裂纹尖端距离矩形板顶部加载端越远，裂纹开始扩展的时间越晚，但是裂纹横向贯穿的时间反而越短，这是由于裂纹倾角越小，越接近于Ⅰ型裂纹，在拉伸载荷作用下，裂纹尖端应力集中越大，更加利于裂纹扩展.

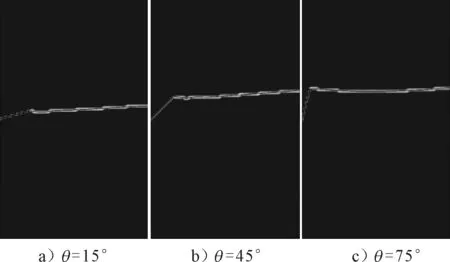
图5 不同初始角度下裂纹扩展过程中的单元状态

裂纹倾角θ/(°)t1/μst2/μsΔt/μs1515.22147.41432.1934514.24749.05634.8097513.76648.74334.977

3.2 裂纹长度的影响

分别取裂纹长度a=20，15，10 mm，采用XFEM计算各裂纹长度下的裂纹扩展路径，裂纹扩展过程中的单元状态见图6.由图6可知，随着裂纹长度变短，裂纹扩展路径的波动性减小，但是仍然基本按Ⅰ型裂纹形式沿直线扩展，说明改变裂纹长度不会使裂纹的扩展路径发生显著变化.表2为不同裂纹长度下，裂纹开始扩展的时间、横向贯穿矩形板的时间和贯穿矩形板的时间间隔.从表中可以看出，裂纹长度越短，裂纹尖端距离矩形板顶部加载端越远，裂纹开始扩展的时间越晚，但是裂纹横向贯穿的时间反而越早，说明随着裂纹长度变短，裂纹扩展的速度变快.从裂纹张开吸收能量的角度考虑，这是由于裂纹越短，其所能吸收的能量越小，当受同样的冲击载荷作用时，裂纹更容易发生扩展.

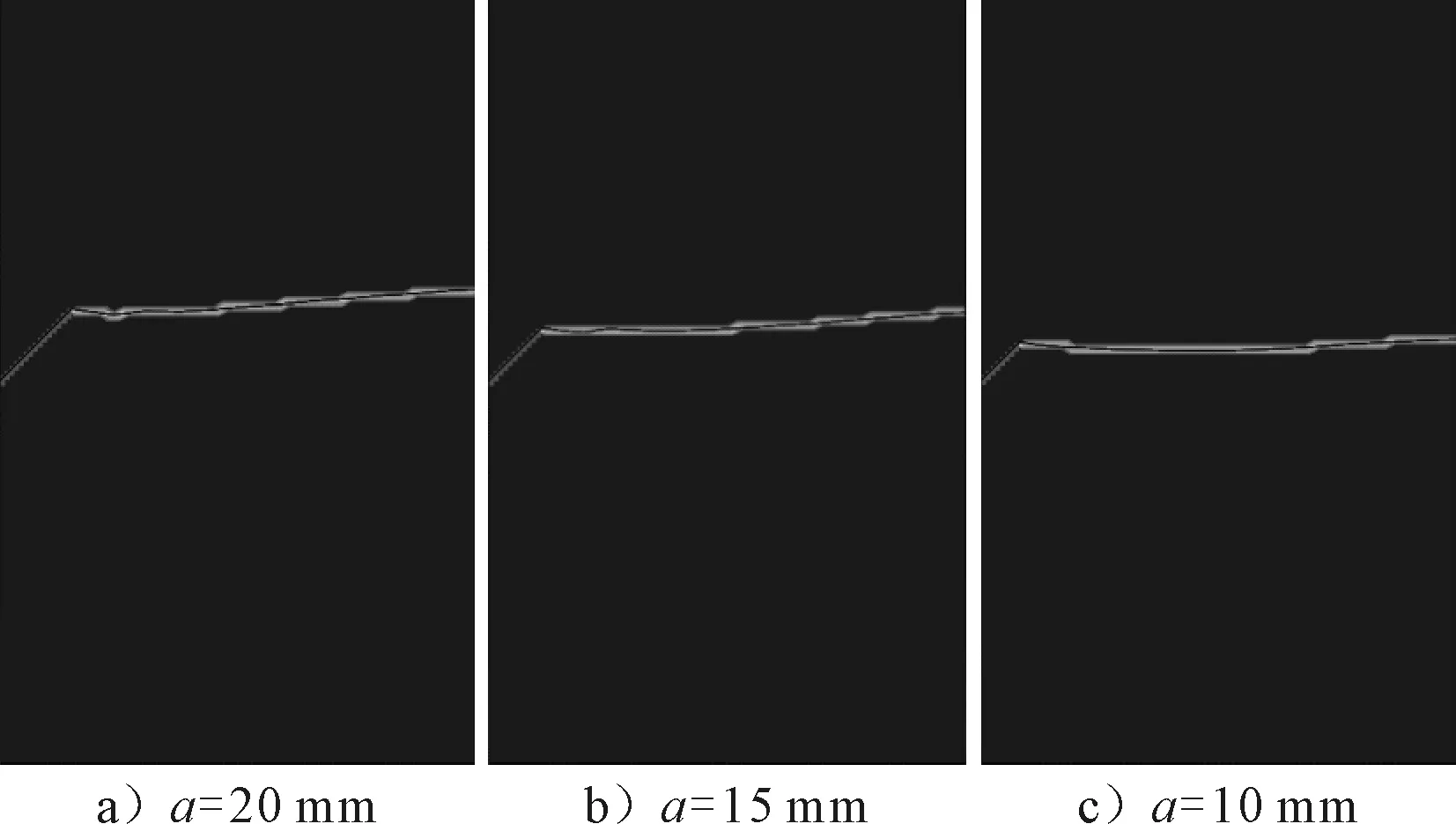
图6 不同长度下裂纹扩展过程中的单元状态

裂纹长度a/mm t1/μst2/μsΔt/μs2014.24749.05634.8091514.54147.99733.4561015.54146.46330.922

3.3 载荷形式的影响

为了进一步研究裂纹的动态扩展特征，将载荷形式由阶跃载荷改为三角形载荷，但总冲量保持不变，见图7.针对图2中的计算模型，图8为三角形载荷下裂纹扩展过程中的单元状态图.

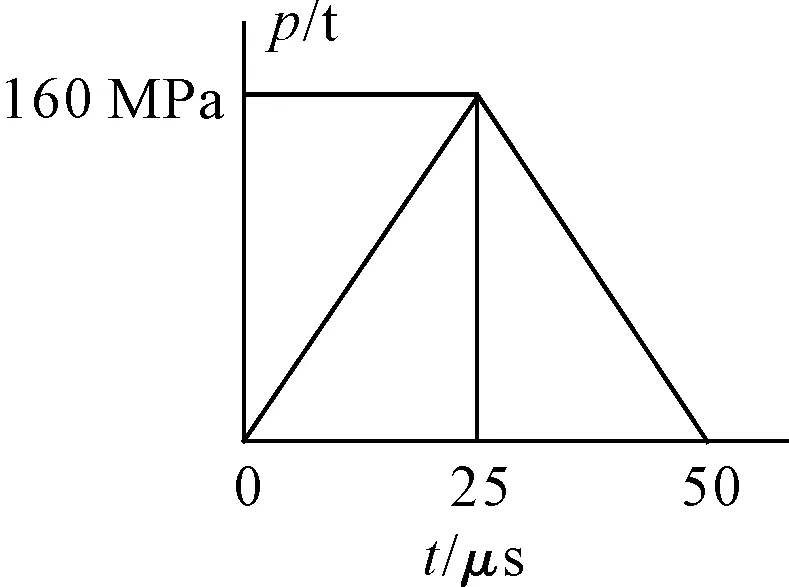
图7 三角形冲击载荷

图8 三角形载荷下裂纹扩展过程中的单元状态

由图8可知，三角形冲击载荷作用下，裂纹相比阶跃载荷更稳定、更趋于按Ⅰ型裂纹形式沿直线扩展，说明载荷总冲量如果保持不变，改变载荷形式不会使裂纹的扩展路径发生显著变化.表3为不同载荷形式下，裂纹开始扩展的时间、横向贯穿矩形板的时间和贯穿矩形板的时间间隔.从表中可以看出，三角形冲击载荷下，裂纹开始扩展的时间比阶跃载荷晚，但是裂纹扩展的速度远比阶跃载荷快，裂纹起裂后不久将横向贯穿矩形板.

表3 不同载荷形式下裂纹开始扩展和贯穿的时间

4 结 论

1) XFEM用扩充的带有不连续性质的形函数基来代表单元内部的间断，在计算过程中，不连续场的描述完全独立于网格边界，可以在规则网格上模拟裂纹沿任意路径扩展而无需对模型进行网格重构，处理断裂问题具有极大优势.

2) 平板斜裂纹基本是按Ⅰ型裂纹形式沿直线扩展，改变裂纹初始角度、裂纹长度和冲击载荷形式不会对裂纹扩展路径产生显著影响，但是对裂纹扩展速度会有明显影响.裂纹倾角越小，裂纹开始扩展的时间越晚，扩展速度越快；裂纹越长，裂纹开始扩展的时间越早，扩展速度反而越慢；在载荷总冲量保持不变的情况下，三角形载荷比阶跃载荷起裂晚，裂纹扩展速度更快.