渗流理论、方法、进展及存在问题*
张李盈,任景莉
郑州大学 数学与统计学院,郑州 450001
如果将一滴水滴到网格上,将会出现什么现象?如果将一些液体倒在多孔材料的顶部,液体能否穿过孔隙,到达材料的底部?如果将一块大型多孔石浸入一桶液体中,石头的中心能否被浸湿?对这类物理问题的思考和研究,产生了渗流和渗流理论。
1 渗流的起源与发展:何为渗流?何为渗流理论?
剥开表象来看,渗流是一类加载在网格、网络或图上的随机过程。渗流系统构成了一种含参数的动力系统,并且当参数经过某一临界值时,系统性质会发生突变,这种突变称为渗流转变或渗透。渗流转变是自然界和人类社会中常见的现象之一。譬如,复杂网络的级联失效过程中,当网络结点或连边的失效概率不超过某个临界值时,失效的节点将仅构成孤立的团簇;反之,失效的节点将构成贯通整个网络的巨大节点集群。这一现象就是一类渗流转变现象,又称为渗透现象。渗流理论是指研究渗流及渗流转变过程中形成的理论模型和方法,包括渗流演化的数学模型、行为特征分析的理论方法及渗流转变临界现象分析的方法和结论等。
图1分四种情况展示了二维正方网格上均匀节点渗流过程中渗流团簇的结构图,其中蓝色表示未被侵占的空置格点,黄色表示被侵占的格点,红色则标记出由被侵占格点构成的最大渗流团簇。p表示网格节点被侵占的概率,是渗流中的重要参数。
图1(a)和图1(b)两种情况下,即侵占p= 0.3或p= 0.5时,系统没有渗透,这时贯通整个网格的巨大渗流团簇没有出现;图1(c)和图1(d)中,即p= 0.592或p= 0.7时,系统发生了渗透,形成了跨越整个网络的巨大渗流团簇。

图1 二维正方网格上均匀节点渗流过程中渗流团簇的结构图(其中蓝色表示未被侵占的空置格点,黄色表示被侵占的格点,红色则标记出由被侵占格点构成的最大渗流团簇):(a) p = 0.3;(b) p = 0.5;(c) p = 0.592;(d) p = 0.7
渗流的思想最早可以追溯到20世纪40年代化学家Paul对聚合物凝结的研究[1-3]。 然而,渗流作为一种数学理论的研究,则起源于1957年工程师Broadbent和数学家Hammersley对防毒面具碳过滤器的设计和研究。Broadbent和Hammersley利用统计方法,深入分析了流体或粒子通过介质时逐步扩散并形成随机路径的过程,并提出了渗流阈值的概念。当侵占概率超过渗流阈值时,渗流系统将形成能够跨越整个介质的巨大渗流团簇[4]。Broadbent与Hammersley的工作被认为是渗流理论研究的开端。
渗流理论主要研究从渗流现象中抽象出来的泛化的数学模型,是对渗流现象的理论描述和分析,是处理强无序和随机几何结构的一种有效的理论方法。统计物理中的相变、临界现象、尺度理论、重整化群、幂律分布与分形理论等常被用来表征渗流的特征和研究渗流问题。渗流理论的形成推动了渗流作为数学理论的研究,使得许多开放性的问题得到了解决。
从理论上看,渗流属于统计物理,概率与统计理论和图(或网络、网格)理论相互交叉的领域。它的研究不仅能够加深对统计物理中临界现象的理解,同时能够推动概率理论的发展。更重要的是,传统的图论加载了渗流,则被赋予了新活力。渗流这个多学科交叉领域,容易使各学科间碰撞出火花,带来新的视角和机遇。
渗流研究发展的短短几十年,有两位数学家因此获得了数学上的最高奖——菲尔兹奖。法国数学家Werner因在随机Loewner演化 (SLE) 理论、二维布朗运动的几何理论与共形域理论 (求解二维网格上非均匀渗流临界指数的理论方法)等渗流相关问题上的杰出工作,获得了2006年的菲尔兹奖[5]。Werner打破了物理与数学的界限,结合概率论与复杂性分析,引入新的思想和概念来解释某些相变中的临界现象 (如从液体到气体的过渡),作出了突出贡献。Werner还获得了欧洲数学学会奖 (2000)、费马奖 (2003) 和Loève奖 (2005)等多项国际大奖。2001年,俄罗斯数学家 Smirnov 证明了三角形网格上临界节点渗流的Cardy公式,进而推导出该渗流的共形不变性[6],并因此获得了2010年的菲尔兹奖。Smirnov 的工作涉及到复杂性分析、动力系统和概率论的交叉。
从应用角度来看,渗流理论源于实践,服务于生产、生活和自然科学的发展。渗流模型不仅易于表述,而且内涵丰富,结论深刻,正好符合了应用的要求。因此,自1957年Broadbent和Hammersley[4]的开创性研究以来,渗流获得了广泛的应用,为实际中的许多问题带来了新视角,提供了新的理论方法。
渗流研究,不论是理论还是应用都具有广阔前景。但是,理论推导的复杂性使得只有少数结果能通过解析方法获得。即便是经典的均匀渗流,常常也只能依赖于数值逼近或启发式方法来获取近似结果。渗流关注网络上的无限集群性(一般都在无限网络上考虑),但是数值模拟只能取有限网络,因此数值模拟在提供一些启发式线索的同时也可能会给出有偏差的结果。基于这两个原因,近几十年来尽管渗流在理论研究方面和应用研究方面都取得了长足进展和令人瞩目的研究成果,可是相关研究远远没有完成,它的理论仍需完善,它的应用仍有广泛研究的价值。
2 渗流中的基本问题
渗流研究因研究视角和侧重点的差异分为两大类:一类侧重于研究结果的可靠性和推理的严谨性;另一类则侧重于应用和物理性质的研究。下面先来介绍渗流理论研究关注的主要问题。
渗流理论研究中,首先需要明确渗流发生的基础网格及其结构。渗流的基础网格,可以是一般的网格,如正方形网格、三角形网格、六边形网格、蜂巢状网格、立方体网格、高维超立方体网格、Bethe网格、纽结型网格、分形结构网格或多重分形网格等,也可以是复杂的网络,如多层复杂网络、相互依赖网络、Erdös-Rényi(ER) 随机网络等;可以是和我们生活休戚相关的物理网络, 如交通网络或物理通信网络 (有线电话或面对面交流网络等),也可以是虚拟的社交网络,如微信、脸书、推特或QQ等等。当然也可以是图论中的图,如定向图、有限图、无圈图等等。渗流问题,可依据它的基础网格称为某某网格 (网络或图) 上的渗流。
确定了基础网格,需要根据具体问题,针对网格中的节点、连边或节点与连边的混合,加载侵占概率,相应的渗流分别称为节点渗流、边渗流和混合渗流。这里加载的概率表示节点或边被侵占、打开、激活或失效的可能性,为了方便叙述,本文中统一表述为侵占概率。渗流过程中,如果网格中的所有节点 (边) 都以相同的概率被侵占,则称为均匀渗流。然而事实上,实际渗流过程中节点 (或连边) 常常具有异质性,因此渗流中应当根据情况赋予节点 (或连边) 不同的侵占概率。这样的渗流称为非均匀渗流。非均匀渗流更为贴合实际,但缺乏完全一致性,因此增加了求解困难。另外,根据渗流加载方式或限制条件的不同,渗流可分为常规渗流,以及衍生而来的爆炸渗流、Bootstrap渗流、定向渗流、关联渗流和受限渗流等等。
加载了渗流的基础网格,将构成网格上的随机动力系统。注意:为了避免混淆,本文中用“渗流”表示网格中的节点 (或边) 经历的缓慢的被侵占过程,用“渗透”表示被侵占的节点形成的跨越整个网格的巨大节点集群 (渗透团簇)。渗流系统的性质将随着渗流过程发生动态演变。随着系统参数的变化,渗流系统会展示出统计物理中的三种相:亚临界相、临界相和超临界相。但是,如果给定了所有参数,渗流过程必处于这三种相中的一种。渗流研究中常常首先建立渗流模型 (确定基础网格和渗流方式),然后对模型进行分析求解,确定渗流模型发生渗透相变的临界条件 (对均匀渗流来说是一个点,称为临界点;而对非均匀渗流来说,是侵占概率空间的一个子空间,称为临界面)、渗流团簇的尺度分布、平均尺度、渗透概率,以及系统处于临界相时,渗流团簇的尺度不变性、自相似性、分形特征、幂律行为与临界指数等等。
2.1 渗流团簇的尺度分布、平均尺度、渗透概率和临界概率
数学与统计物理中,渗流理论描述了随机图中连通簇的随机行为,涉及到团簇聚类、临界性、扩散、分形、相变和无序性等。为了表述方便,设G为渗流的基础网格,为渗流中基础网格上节点 (边,或节点与边的混合)被侵占的概率。这里如果是个标量(一维向量),则称为均匀渗流;反之,如果是大于一维的向量,则为非均匀渗流。渗流过程中会形成各种大大小小不同尺寸、不同结构的由被侵占节点 (节点渗流)构成的连通子集,称为渗流团簇,记为C。渗流团簇的尺寸指渗流团簇中包含的被侵占节点的数目,记为|C|。渗流团簇中尺寸无限大或与基础网络具有相同量级的 (或者能够贯穿整个基础网络的) 团簇被称为渗透团簇。渗透团簇中的节点能够从基础网络一端延伸到另一端。所有可能尺寸的渗流团簇构成的集类记为;所有尺寸为s的渗流团簇构成的集类记为(s= 1, 2 ,…),并用表示所有渗透团簇构成的集类。当渗流系统处于亚临界区域时,是空集,此时系统不存在渗透团簇。对于边渗流问题,节点自动被侵占,此时渗流团簇指由被侵占的边依次连接节点构成的子连通集。混合渗流中,渗流团簇指由被侵占的节点和被侵占的边依次连接而成的子连通集。
渗流中常常关注这几个问题:①所有渗流团簇的尺度分布,即不同尺寸渗流团簇出现的概率;②渗透发生的临界条件和渗透发生的概率;③所有有限尺度渗流团簇整体的平均尺寸。
首先考察渗流系统中团簇尺寸的概率分布。渗流过程中会形成各种不同尺寸的 (由被侵占节点构成的) 团簇:有的尺寸很小,最小的可能只包含一个被侵占节点,对应的团簇尺寸为1;最大的可能会包含无穷多个节点,对应尺寸为无穷,比如渗透团簇。依据概率与统计的关系,所有这些不同尺寸的团簇,可以看作渗流过程中渗流团簇可能分布的很多次实现,当然需要基础网格足够大,而且多次实现并取平均值才可能逼近渗流团簇真实的尺度分布。这如同把渗流团簇的尺寸看作随机变量,考察这个随机变量的概率分布。类似地,大街上人们有着多种多样的身高,引入随机变量来考察从中任取一个人身高的概率分布。这种考察方式的合理性可由概率论中的大数定律得到保证。
我们可以通过多次实验,模拟渗流过程,然后统计不同尺寸团簇所占的比例,以此统计值作为团簇的尺度分布。这种做法类似于通过多次实验得到统计值,利用统计值的多次平均值去代替事件在每次实验中发生的概率。经验告诉我们,有时这种近似会产生偏差,但大数定律保证只要实验次数足够多,这种偏差在概率意义下可以无限小。即当实验次数趋于无穷时,这个实验的统计值的平均将依概率收敛到渗流团簇真实的尺度分布。这种基于大数定律,通过统计分析获得渗流中团簇的尺度分布、平均尺寸、渗透概率、临界条件等的数值近似结果,称为蒙特卡罗(Monte Carlo) 数值模拟法。由于渗流团簇这种随机几何体结构的复杂性,基于统计实验的数值模拟(numerical simulation)成为目前渗流研究中广泛采用的一种方法。
渗流研究也常常基于概率论中的基本理论和方法,通过理论推导来获得渗流团簇真实的尺度分布,以此作为渗流中不同尺度团簇出现的概率。这种方法称为解析推理法。解析法是与数值方法相对的方法,以概率论为基础,通过解析方法,直接推导渗流团簇的尺度分布、平均尺度、渗透概率、临界条件等的精确结果[7]。下面以二维正方形网格上均匀的节点渗流为例来说明解析方法。对二维正方形网格上的均匀节点渗流,将尺寸为s而周长为t的渗流团簇记为st-团簇,所有尺寸为s的团簇统一记为s-渗流团簇。bs,t表示不同st-团簇的个数。令A(s,p) 表示随机事件——任取一个节点属于s-渗流团簇,这里p表示节点侵占概率,s的可能取值为0, 1, 2,…,∞。考虑到渗流过程中节点独立地被侵占,可推出下式:

式(1)中,对较大的s,由于渗流团簇结构的复杂性,相应的t和bs,t很难确定,从而导致解析方法的困难[8]。
从图2(a) 能够发现,当系统尺寸N趋于无穷大时,一维网格上均匀渗流的渗透概率趋向于在临界点(侵占概率的) 发生跳跃的阶跃函数。这是一个非常特殊的系统。对于一般渗流系统,例如二维正方形网格上均匀渗流系统,当系统尺度L趋于无穷时,渗透概率趋向逐渐光滑函数,且在临界点函数值突发地从零转变为非零(图2(b))。
对于大多数渗流问题,我们没有办法通过解析方法解出渗流主要输出量,这时候只能求助于数值模拟。事实上,渗流中现有的重要结论大多是通过数值模拟获得的近似结果。虽然数值模拟简单直接,易于实现,也能给出一些有指导意义的结论,但是数值模拟的过程应当遵循统计中规范的理论和方法,否则所得结果可能毫无意义,并且有可能将我们引入歧途。实际模拟过程中,无论我们将基础网格的尺度取多大,都只能是有限值,而大数定律只有在实验次数趋于无穷时,其误差才能在概率意义下被忽略。实际上,当系统的尺寸变得越来越大时,估计值围绕着真实值的波动幅度会越来越小,并且在概率意义下估计值不断逼近真实值。有限尺度情况下的模拟,为了降低误差,需要在给定侵占概率p的条件下多次重复实验,并求其平均值。
为了表述方便,不论是均匀渗流还是非均匀渗流,统一用p表示侵占概率。此时系统中的节点 (或边),可看作以概率p被侵占,也可看作以概率1-p空置。用“s-渗流团簇”表示由被侵占节点构成的尺寸 (团簇包含的被侵占节点的数目) 为s的连通子集。
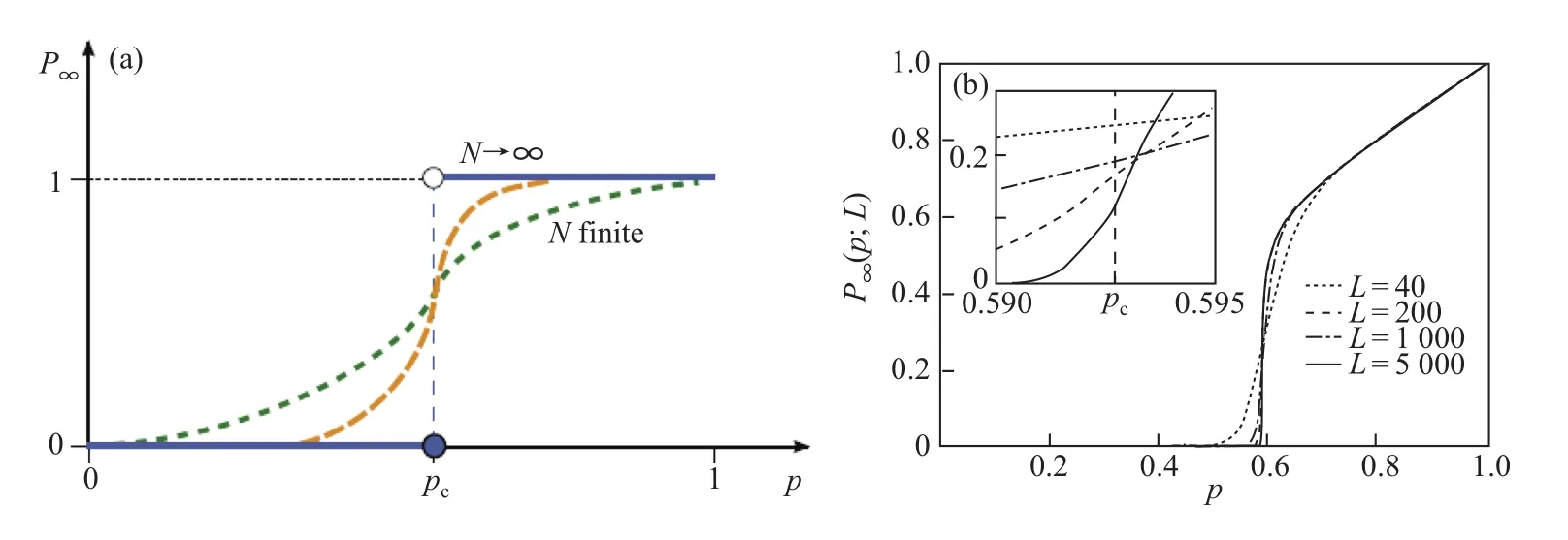
图2 (a)以系统尺寸N为参数,一维网格上均匀渗流的渗透概率与侵占概率之间的函数关系示意图[9];(b) 以系统尺寸L为参数,二维正方形网格上均匀渗流的渗透概率与侵占概率之间的函数关系示意图[8]
实际上,基础网格的空间分布常常导致大尺度渗流团簇空间拓扑结构的复杂性,从而导致解析推导的困难,使得渗流团簇的尺度分布很难确定。若能确定渗流团簇的尺度分布,相应地可得到渗流转变现象发生的临界条件、渗透概率和有限渗流团簇的平均尺寸。
若渗流系统中出现渗透团簇,则称整个基础网格被渗透。任选一个节点属于渗透团簇的概率称为系统的渗透概率,记为P∞(G,p),则有
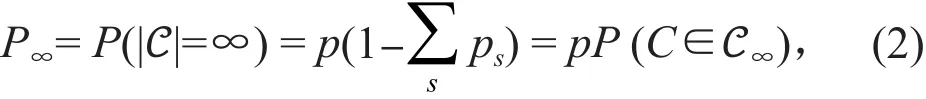

渗流过程中以下基本共识成立,即存在pc,使得
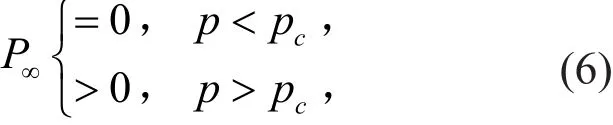
其中,pc称为临界 (侵占) 概率。非均匀渗流中,临界侵占概率构成了侵占概率空间中的子空间,称为临界面。这是系统渗透 (发生渗流转变) 的临界条件。pc定义如下:

不论系统是否渗透,有限尺度渗流团簇的平均尺寸都可以表示为

2.2 普遍性和物理相
渗流过程中,临界侵占概率pc具有局部敏感性,与基础网格的结构和渗流加载方式都密切相关。渗流团簇的尺度行为,在临界点和临界点附近则具有普遍性,即只与系统维数有关,而不受基础网格结构和渗流方式的影响。这种普遍性还意味着,对于给定的维数,在临界点pc附近,各种临界指数以及渗流团簇的分形维数都与基础网格的类型和渗流加载方式相互独立。某种程度上来说,研究渗流团簇的这种普遍性行为具有重要的研究意义。然而,近年来Hassan对加权面板随机网格 (weighted planar stochastic lattice,WPSL)上的渗流研究发现,尽管网格的维数与它所嵌入的空间维数一致,但它的临界指数却与平面上其他已知网格的有所不同[11-12]。
前面已经提到,侵占概率的变化会导致渗流系统处于三种不同的物理相,即亚临界相、临界相和超临界相。亚临界相最重要的特征是“指数衰减”,即当p<pc时,一个确定的节点属于一个尺度为s渗流团簇的概率,随着s的增大以指数形式衰减。Menshikov在1986年[13],Aizenman和Barsky 在1987年[14]分别独立地证明了这个结论的正确性。
另外,二维平面上正方形网格ℤ2的对偶网格(dual lattice)也是一个正方形网格,这说明平面正方形网格的超临界相与其亚临界相也具有对偶关系。这为平面正方形网格的超临界相分析提供了基本而充分的信息。我们知道,对ℤ2上的均匀渗流,当边的侵占概率p<pc时,一定会存在一个跨越整个网格的由没有被侵占的边 (闭合边)依次连接节点构成的团簇(称为闭合团簇)。系统的渗流团簇(由被侵占的边或称为打开的边依次连接节点构成的团簇)在亚临界相彼此独立且尺度有限,因此淹没在了尺度无限的闭合团簇族中。当p>pc时,相反的事情会发生,即系统的闭合团簇越来越少,尺度也越来越小,并且随着侵占概率的增大逐渐淹没在巨大渗透团簇的海洋中。维数d≥3的网格中,类似的对偶分析将变得越来越复杂。
渗流模型存在奇点,奇点处渗流系统处于临界相,渗流系统在临界相会展示出分形特征和幂律行为。尺度理论可以分析临界点附近渗流量的临界指数。临界指数与维数d相关,当d= 2时,临界指数可通过共形场理论、Schramm-Loewner进化理论或数值模拟来求解。关于临界指数,目前只有d= 2和d≥19经过了严格的证明。此外,d= 2时,大尺度渗流团簇具有共形不变性。当d≥ 19时,临界指数可通过花边扩展(lace expansion) 法来求得。渗流与花边扩展之间的联系是 Hara 和 Slade 在1990年发现的[15]。 用对偶理论可以证明,二维平面中很多网格上的渗流在临界点上都不会发生渗透。随后,Schramm猜想平面网格上渗流中大尺寸团簇的尺度极限可以用 Schramm-Loewner 进化理论来描述。2001年,Smirnov证明该猜想在平面三角形网格上的节点渗流中是正确的[6],并因此获得了2010年的菲尔兹奖。
2.3 尺度分析与临界指数
渗透团簇的突然出现常伴随着一系列特征的突变,因此渗流转变是一种临界行为。这种临界行为在临界点附近具有普遍性,包括临界指数和多标度律。普遍性意味着临界系统的大尺度行为可以用相对简单的数学关系来描述,这种关系完全独立于小规模的结构。这使得人们能够研究和理解一系列非常广泛的系统行为, 而不需要知道太多细节。例如:渗流模型临界指数的普遍性使得它只与基础网格所在空间的维数有关,而不受网格结构 (如平面中六边形网格、三角形网格和正方形网格上的渗流) 和渗流方式 (节点渗流、边渗流、混合渗流、高阶渗流) 的影响。
尺度分析过程中,引入了两个特征量:特征长度 (又称为相关长度)ξ和渗流团簇的特征尺度sξ。其中:ξ指所有有限尺度渗流团簇中尺度最大团簇的典型半径 (the typical radius of the largest cluster),标志着节点对节点相关函数的快速衰减点;sξ指所有有限尺度团簇中尺寸最大团簇的典型尺寸,标志着系统渗流团簇尺度分布的幂律衰减与快速衰减的分段点。这里节点对节点相关函数指对某个已经被侵占的节点,与它距离r的节点也被侵占了的概率。一般来说,渗流团簇具有分形结构。若假设渗流团簇的分形维数为D,则

当系统处于亚临界或超临界相时,对于给定的侵占概率p,渗流团簇的相关长度ξ和特征尺度sξ都取有限值。随着p越来越靠近临界点,它们的值也越来越大。事实上,当p趋近于pc时,ξ和sξ都趋于无穷大。当渗流系统的侵占概率p在临界点pc附近时,下式成立:
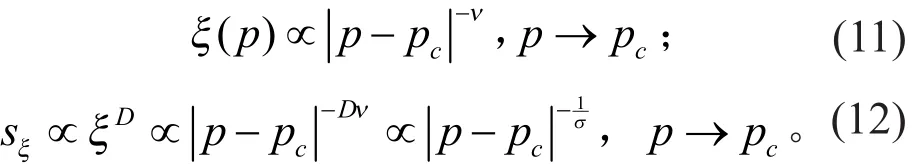
渗流团簇的分形维数则满足

因此,当系统处于临界相时,渗透团簇表现出幂律行为、尺度不变性、自相似性和分形特征。此时若假定基础网格的尺度为L,渗透概率与网格窗口尺度有关,记为P∞(L),且有

这里D是渗流团簇的分形维,d是网格维数,一般D≤d。若D<d,当L趋于无穷时,P∞(L)将趋于零。
此时,对于尺度为s的有限渗流团簇,

这里,Rs是尺度为s的渗流团簇的平均半径。首先计算某个s-渗流团簇的中心位置rc,其中r表示该s-渗流团簇中包含的编号为k被侵占的节点所在的位置;然后计算该团簇的半径最后对所有s-渗流团簇取平均值,得到Rs。
临界面板p=pc上,渗透团簇展示出自相似分形特征;进入超临界区域p>pc,渗流团簇则表现出从分形交叉的几何特性[8]。系统处于超临界相p>pc时,相关长度ξ和渗流团簇特征尺度sξ都取有限值。此时,

渗流团簇的相关尺度ξ不仅标识了有限尺度渗流团簇的最大半径,根据有限尺度效应,ξ同时也标识了空置节点形成的有限尺寸孔洞的最大半径。因此,当窗口尺寸小于ξ时,渗透团簇展示出分形特征,而大于ξ时,由于孔洞消失,则表现出均匀特征。
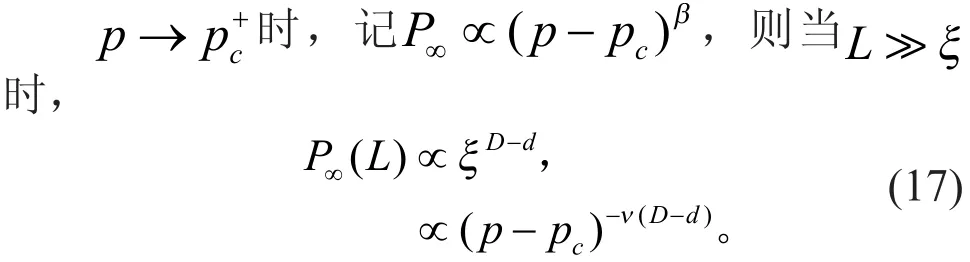
渗流系统接近临界相时,有限团簇的平均尺寸、相关长度、特征团簇尺度和尺度分布的k阶矩等几乎都会发散。假设时,渗流团簇的平均尺寸

尺度理论表明,渗流临界点pc附近,尺寸为s的渗流团簇的平均数量平均周长平均团簇半径密度依赖于到团簇中心的距离r。临界点附近,主要量的表达式中涉及到7个临界指数α、β、γ、δ、ν、σ、τ。多标度律表明,d维空间中临界指数之间满足:表1列出常见网格上渗流的临界指数。
3 研究进展及存在问题
渗流模型定义简单,容易描述。模型最常关注渗流过程中的最优路径和最优时间。首个渗流模型中所有边都以相同的概率独立地被侵占,即随机地赋予基础网格所有边独立的两点分布。这些两点分布一起构成了多重伯努利分布,称为伯努利边 (bond) 渗流[17]。随后,一般化的“Fortuin-Kasteleyn随机团簇模型”被引入,此模型与Ising模型和 Potts 模型紧密相关[18]。 接着, Gilbert 将伯努利边渗流加载到一个含有N个节点的完全图上,获得随机图,记为G(N,p)。这是一类被广泛关注的随机图,著名的Erdös-Rényi随机图只是它在某个点上的快照。这类渗流问题中临界概率

表1 常见网格上渗流的临界指数[8]
标准渗流是处理网络上复杂动态过程的有效模型和理论方法,因此广受关注。渗流理论的广泛应用为它带来新的研究视角,衍生出多种进化的渗流模型,如首穿渗流、入侵渗流[19]、定向渗流、Bootstrap渗流、爆炸渗流等。1965年Hammersley与Welsh提出了首穿渗流,用来解决加权图上的随机距离、两点间最小路径或随机几何的大尺度行为。首穿渗流成为概率论一个经典的研究领域。1983年Wilkinson和Willemsen引入了入侵渗流,用以描述现实中流体缓慢流经孔隙材料的行为特征[20]。1984年Durrett在《概率年刊》上发表了关于二维定向渗流的研究成果[21]。定向渗流是从接触过程中抽象出来的一类渗流问题。Bootstrap渗流则通过删去团簇中邻居数较少的节点来考察团簇的连通性[22]。爆炸渗流[23],与标准渗流模型相比,常常表现出不连续的相变。随机图中爆炸渗流的连续相变(二级相变) 或不连续的相变(一级相变,如水在零度凝结时伴随着熵的不连续下降),由于收敛速度慢,很难通过数值计算来实现。最初,人们认为随机网络中“Achlioptas”过程下的相变是不连续的,因而称之为“爆炸渗流” 。 最后证明,这种转变的热力学极限实际上是连续的。此外,1989年Chayes等研究了伯努利渗流高密相的相关长度,结果也发表在《概率年刊》上[24]。1993年英国剑桥大学的Grimmett教授等研究了渗流模型中无限集群上的随机游走[25]。1994年Berg和 Maes在《概率年刊》上发表了关于马氏域中的分歧渗流[26]。
近年来,随着复杂网络研究的兴起,渗流研究也扩展到各类复杂网络上。相邻节点对之间度相关的随机网络,称为随机“相关(不相关)网络”。1999 年Newman等考察了小世界网络上节点渗流,作为疾病传播模型推导出了渗透概率的近似表达式[27]。2000 年Cohen等考虑了一般的不相关无标度网络上渗流问题,其中每个节点的移除概率都与它的度有关联[28]。同年,Hara和Slade研究了高维渗流初期无限集簇的尺度极限[29]。2001年Newman考虑了具有任意度分布的不相关随机网络上的渗流问题,用生成函数法推导其最大连通团簇和渗流阈值[30]。他们发现无标度网络中的巨型连通团簇对随机攻击具有稳健性,但易受到高度密集定向攻击的破坏[31-32]。基于生成函数法,度相关网络上的渗流也获得了深入研究[33-36]。2001年,Callaway等研究了生长网络上一类简单模型的渗流相变[37]。2007年Acín等研究了量子网络中的缠结渗流[38]。2011年Serrano等研究了自相似网络中的渗流,证明自相似网络中一般图上的渗流具有零渗流阈值[39]。2012年Lau等研究了二分网络上的凝聚渗流,发现自发对称性破缺造成了渗滤阈值附近的非普适性行为[40]。2015年D′Souza和Nagler研究了爆炸渗流中的反常临界和超临界现象[41]。同年,Radicchi研究了实际相互依赖复杂网络上的均匀渗流,讨论了临界概率及渗流转变的连续性问题[42]。2016年Hackett等研究了多层复杂随机网络上的边渗流。讨论了临界概率、渗透概率和临界点相变特征[43]。更一般地,网络上的Bootstrap渗流[44]、k核渗流[45]都得到广泛的研究。
特别地,临界概率作为渗流的一个重要特征一直是渗流研究的热点。渗流过程中临界侵占概率或侵占概率临界面上,渗流系统的行为会发生突变,从没有渗透到渗透。临界概率不具有普遍性,它不仅依赖于网格的空间维数,还和网格结构的细节密切相关,并且仅在无限维的极限下才能达到平均场值[46]。 追求精确的渗流阈值或对其界限进行严格证明,是数学家们追求的一个经久不衰的研究领域[10,47-48]。
早在1963年和1964年,Sykes和Essam就推导出平面中三角形网格上的节点渗流对应的临界概率pc为0.5。平面中,三角形网格、简单的二次网格与蜂窝状网格上边渗流对应的临界概率pc则分别为2sin(π/18)、0.5、1-2sin(π/18)[49-50]。1979年Wu曾猜想,棋盘形网格上非均匀渗流的临界流形 (侵占概率的临界面) 应该满足

其中,C(p,r,s,t)=1-pr-ps-pt-rs-rt-st+prs+prt+pst+rst,p、r、s、t分别是每个正方形格子4条边上的侵占概率[51]。1980年美国康奈尔大学的Kesten教授证明正方形网格上边渗流的临界概率等于0.5[47]。随后,1984年Wierman通过星三角变换,确定纽结型网格上均匀边渗流的临界概率应满足[48]
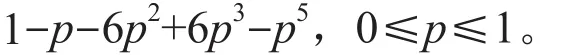
值得注意的是,2001年俄罗斯著名数学家Smirnov证明了平面中三角形网格上节点渗流的Cardy公式,并由此导出渗流的共形不变性和尺度极限[6]。Smirnov的理论完善了平面中三角网格上渗流,并且和著名的Schramm-Loewner演化密切相关[9]。Smirnov的杰出工作使他获得了2010年的菲尔兹奖。到2006年Ziff证明所有能分解为某种三角形排列的网格(称为自对偶)可通过星三角变换得到其精确渗流阈值。此后,2012年Ziff 等又给出纽结形网格上的五阶渗流的临界渗流面(临界渗流流形):

其中B(p,r,s,t,u) =C(p,r,s,t)-u(1-pr-st+prst),并证明了Wu在1979年的猜想。2013年,Grimmett利用星三角变换将Kesten在1980年的结果从正方形网格上的边渗流扩展到三角形和六边形网格上,证明这些渗流问题在临界点(临界面) 上具有盒子交叉性 (RSW理论),为证明这些过程的普遍性和共形不变性迈出了重要的一步,并为非齐次系统临界点提供了新的证明思路。表2列出了常见网格上均匀节点渗流和边渗流对应的临界侵占概率。
对于非均匀渗流,到目前为止,除了Wierman在1984年与Ziff在2012年给出的纽结网格上的四阶和五阶渗流的临界面以外,就只有平面中正方形网格上的二阶边渗流,以及三角形网格与六边形网格上的三阶边渗流的临界面,它们的形式如下[52]:

这里三角形网格与六边形网格具有对偶关系[10],因此它们边渗流的临界概率之间也有对偶关系。事实上,平面中一般网格上的边渗流与其对偶网格上的边渗流的临界点 (或临界面) 之间有如下关系:故,

经过50年左右的研究,渗流理论已经获得了丰富的研究成果,但仍有许多开放性的问题没有解决。 到目前为止,即便是经典的正方形网格、蜂窝状网格、六边形网格和三维立方体网格上均匀节点渗流问题的临界概率,Kagomé网格和立方体网格上均匀边渗流问题的临界概率,仍没有精确的结果。部分结论只能建立在数值模拟和近似算法的基础上,有待进一步的研究。

表2 各类常见网格上的均匀节点渗流与均匀边渗流对应的临界侵占概率
渗流理论具有广阔的应用前景,但理论推导的复杂导致了研究的困难。到目前为止,只有少数结果能通过解析方法获得,是因为网格结构导致了渗流团簇拓扑结构的复杂多样性。即便是经典的均匀渗流,至今也只有一维网格和Bethe网格[53]上获得了精确的解析表达式。均匀渗流忽略了节点(或连边)渗流过程中的异质性,对所有节点赋予相同的打开(或失效,侵占)概率,因此常常具有较好的齐次性,这使得理论推导要简单很多。更多的网格,如简单的正方形网格、三角形网格、六边形网格、立方体网格、超立方体网格等,这些网格上的渗流问题常常只能依赖于数值模拟或启发式方法来获取近似结果。此外,运算的复杂性也导致现有的研究多数集中于均匀渗流。均匀渗流尽管简化了运算,但是忽略了渗流过程中的异质性,与实际有一定差距。事实上,由于网格结构的不规则性,或者规则网格中节点 (或连边) 属性的不同,应当在渗流中赋予节点不同的侵占概率,这样的渗流称为非均匀渗流。非均匀渗流贴合实际,但缺乏齐次性,较难求解,因此相关研究屈指可数。尽管如此,在研究者的不懈努力下,非均匀渗流已经取得了一些研究成果。1982年,Kesten研究了简单正方形网格上的二阶非均匀边渗流,获得临界侵占概率的表达式[52]。 随后,1994年Zhang等研究发现,对于正方形网格上的二阶非均匀边渗流,如果让有一个定点在x轴上的边以小于1的概率被侵占,那么临界面上不会发生渗透现象[54]。到2013年,Grimmett利用RSW理论将Kesten 1982年的结果扩展到了三角形和六边形网格上的三阶[55]。2016年和2017年,Ren和Zhang等分别研究了经典Bethe网格与带节点随机分布的不规则Bethe网格上的非均匀节点渗流[7,56]。
作为应用广泛的一种数学理论,过去的50年中,渗流理论为物理[4,57-59]、 材料科学[26,60-65]、复杂网络[22,28,42,66-69]、疾病传播[33-34,70-74]、信息传播[32,75]、化学[1-3]等领域中的众多问题提供了新的思想方法。
1969年,Holcomb等利用渗流理论分析了掺杂半导体在导电性变化过程中的详细特征[61]。1994年Berg与Steif将渗流用于气体分析,建立了硬核网格上的气体模型[76]。2009年Ward等利用渗流理论研究了电子相分离的锰氧化物上弹性驱动的各向异性[75]。 2011年Nagler基于渗流理论,研究了单一链在竞争中的影响[77]。2012年Baxter等利用渗流理论研究了相互依赖网络的突然崩塌[66]。2015年Chen等利用渗流理论分析了金属玻璃微观结构中的短程有序性与长程无序性,认为液体相原子的渗流导致了非晶特殊的微观结构。该结论发表在《Science》上并引起广泛关注[60]。2016年Lemoult等利用定向渗流理论研究Couette流中持续动荡的转变[78]。2017年,基于渗流理论,Radicchi和Bianconi研究复杂网络的稳健性,发现不同网络层之间的依赖关系能够加强网络整体的稳健性[68]。在目前这种复杂网络普遍存在并与我们生活休戚相关的大环境下,Radicchi的研究结果有助于提高复杂网络运行过程的可靠性,从而减少灾害发生时造成的影响。同年,Sopu等将渗流用于非晶合金剪切带成核过程原子水平变化的分析,认为控制非晶态金属塑性变形能力的是剪切转变区的渗流能力[65]。总而言之,渗流理论在实际中的应用总是能带给我们希望和惊喜。
渗流理论作为多学科交叉领域具有重要的理论和应用研究价值,但渗流团簇结构的复杂性和解析推理的困难导致现有的研究多依赖数值模拟,且主要集中于均匀渗流,而实际中网格常常展示出随机或混合随机性。 比如,材料科学家通过X射线衍射发现无序结构材料非晶合金的微观结构展示出短(中)程有序而长程无序[16,47,79],这使得它的结构形成了一种混合随机网络;再比如,微信、QQ、推特等社交网络的用户随时会登陆或退出系统,也会随时添加或删除好友,导致网络结构的随机性或混合随机性。此外,宿主具有迁移特征的疾病传播网络,随着宿主迁移范围和方式的不同也会表现出随机或混合随机性。根据作者的工作和理解,认为下面的几个问题值得进一步考虑。
对渗流理论的研究可以考虑:①建立随机和混合随机网格上的非均匀渗流模型,并通过解析方法求解分析模型。事实上,尽管对于渗流问题解析结果很难获得,然而具有树状结构的Bethe 网格,它特殊的结构使得渗流问题可以通过解析方法求解。②建立随机和混合随机Bethe网格上的非均匀渗流模型,并通过解析方法求解分析模型。③研究渗流过程的演化与离散时间动力系统的关系,将离散动力系统的研究成果引入到渗流的分析。
相关的应用可以研究:①将非均匀渗流理论引入无序结构材料——非晶合金与高熵合金的研究中,建立与材料微观结构相吻合的随机或混合随机非均匀网格上的非均匀渗流模型,模拟材料的微观结构;②利用随机和混合随机Bethe网格上的非均匀渗流理论,分析非晶合金的动力学行为和塑性流变行为;③利用随机和混合随机网格上的非均匀渗流,分析社交网络上的信息传播或宿主带有迁移特征的疾病传播网络上的传染病传播。当然,其他还有很多重要的理论和应用问题有待进一步考虑。

