应力效应对tP10-FeB4的电子结构与光学性质的影响

董明慧， 王学文， 苑光明， 张彩丽

(1. 齐鲁理工学院，济南 250200; 2. 太原理工大学材料科学与工程学院，太原 030024)

1 引 言

金属硼化物由于具有高强度、高硬度、良好的导热、导电和化学稳定性得到了广泛的应用. 但是自然状态的金属硼化物几乎没有，因此广泛应用的金属硼化物几乎都是人工合成的[1]，比如OsB2[2]、ReB2[3, 4]、FeB4[5, 6]、CrB4[7]、MnB2[8, 9]、TcB2[8, 9]等. 其中FeB4由于硬度高、光电性能优良等特点是潜在的半导体材料. Kolmogorov[10]研究发现FeB4具有两种不同的结构oP10-FeB4(空间群Pnnm)和oP12-FeB4(空间群Pnma)；Bialon[11]认为在高压下oP10-FeB4比oP12-FeB4更加的稳定. 但是Zhang[6]和Wang[12]研究发现虽然oP10-FeB4硬度很高但却没有达到超硬度材料的要求(40 GPa). 2014年Wang[13]经过深入研究发现了FeB4的另外一种结构tP10-FeB4，tP10-FeB4由于硬度高达45.4 Gpa，是理想的超硬材料. 目前来看关于FeB4不同结构性质的研究基本都是在理想状态(0 K，0 Gpa)下进行的[6,13,14]，而从目前的工业应用情况看铁硼化物很多都应用于高压的工况下[13]，因此非常有必要研究压力对铁硼化物尤其是对tP10-FeB4的物理性质的影响. 鉴于此，本文利用密度泛函理论深入研究了tP10-FeB4的电子结构和光学性质.

2 计算方法

计算过程使用的是Material Studio软件中的CASTEP模块[15, 16]，采用的是基于密度泛函理论(DFT)[17]的第一性原理平面波赝势方法，交换关联能采用的是广义梯度近似(GGA)中的PBE[18]方程，Fe和B的价电子分别为3p63d74s1和2s22p1，平面波截断能设定为380 eV，为保证计算收敛，Monkhorst-Pack[19]k点网络密度选取的为6×6×6，自洽收敛条件设为：总能量小于1.0×10-5eV/atom，最大Hellmann-Feynman力偏差小于0.01 eV/atom，最大应力偏差低于0.05 GPa，最大位移偏差低于5.0×10-3nm，计算过程中充分考虑了自旋极化.

3 结果讨论

3.1 晶体结构性质

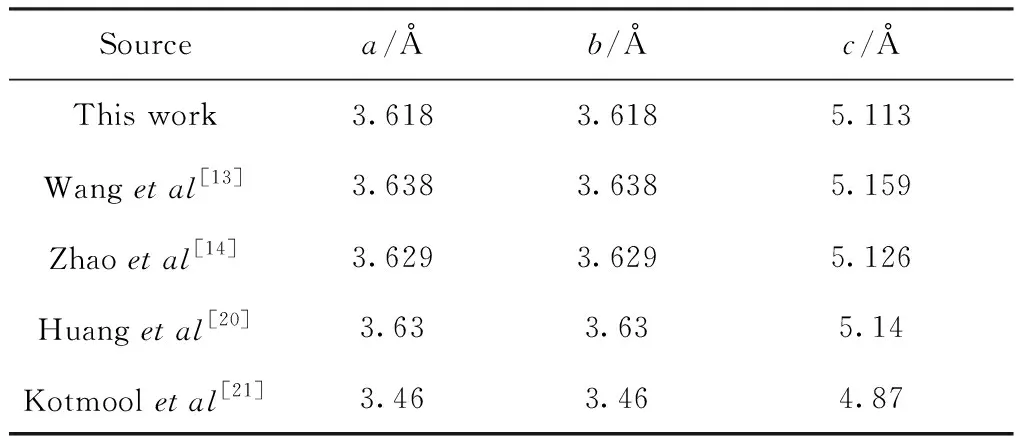
tP10-FeB4属于四方晶系，空间群为P42/nmc，从图1中可以看出1个Fe原子四周包围着4个B，其中Fe(2b)占据(0，0，0.5)坐标、B(8g)占据(0.250，0.5，0.628)坐标表1列出了计算得到的平衡晶格常数分别为a=3.618 Å，b=3.618 Å，c=5.113 Å. 对比其他人的理论和实验结果(Wang等人[13]，Zhao等人[14]，Huang等人[20]), 发现我们的计算结果和其他人的吻合的非常好，偏差小于1%，但是Kotmool等人[21]得到的结论与本文中的偏差较大，大概在5%左右，这主要是因为Kotmool在优化晶胞过程中采用的是基于遗传算法的软件包(USPEX)[22, 23]. 因此总体上分析，本文计算方法的精度和可信度上是符合计算要求的.

另外，我们还研究了理想状态下(0 K，0 Gpa)tP10-FeB4的带隙发现带隙宽度Eg=1.773 eV，与文献中的计算结果(1.85 eV[13]，1.77 eV[14])吻合的很好. 但是相比于GW算法略低(2.43 eV[14])，这主要是因为使用密度泛函理论得到的能隙偏小[20].

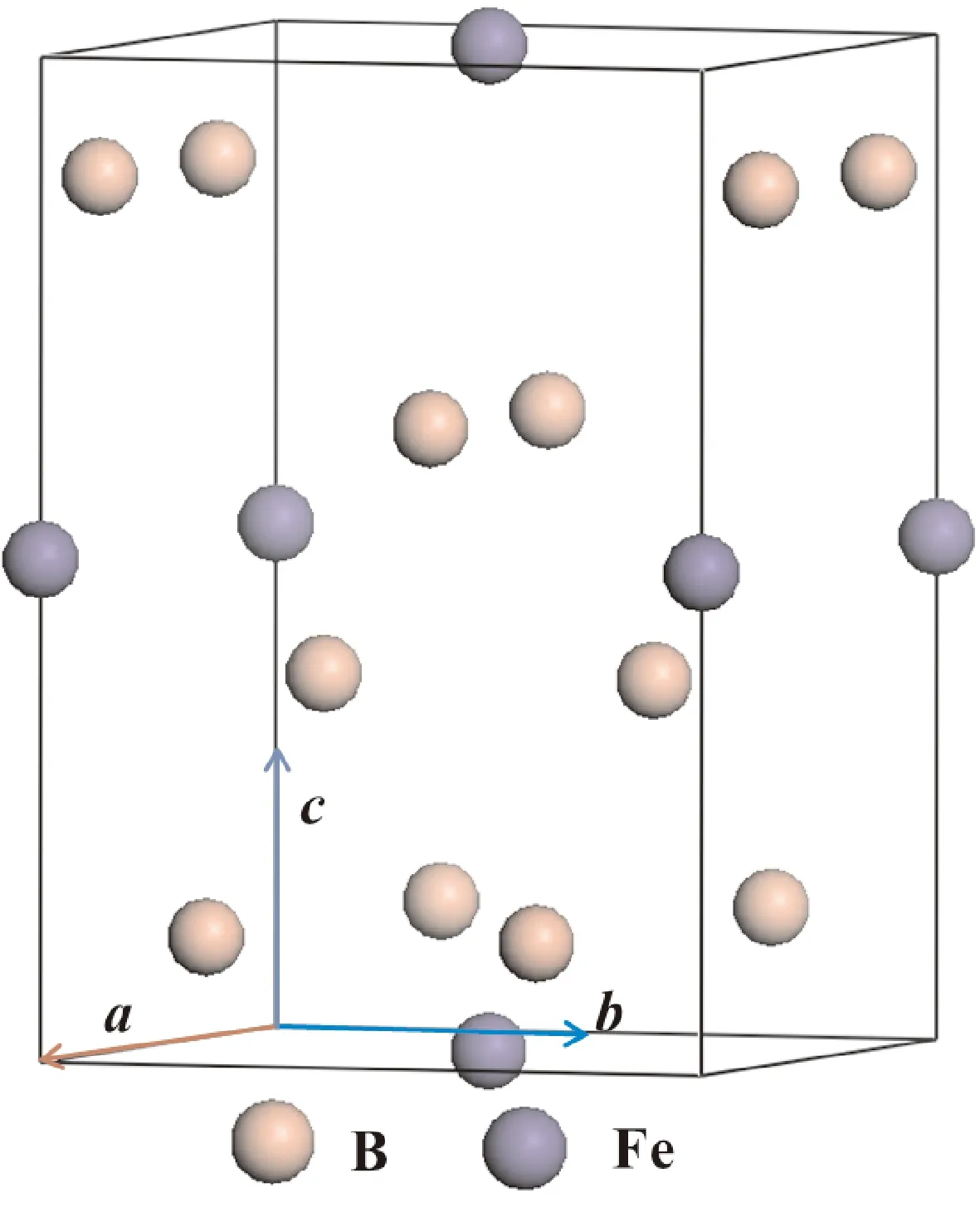
图1 tP10-FeB4晶体结构Fig. 1 The crystal structure of tP10-FeB4

表1 计算得到的tP10-FeB4平衡态晶格常数a,b,c

Table 1 Calculated equilibrium lattice parametersa,b,cof tP10-FeB4

Sourcea/Åb/Åc/ÅThis work3.6183.6185.113Wang et al[13]3.6383.6385.159Zhao et al[14]3.6293.6295.126Huang et al[20]3.633.635.14Kotmool et al[21]3.463.464.87

3.2 压力对tP10-FeB4电子结构的影响

为研究应力对tP10-FeB4电子结构的影响，计算过程由单纯的结构优化转为分子动力学模拟. 计算过程采用的模型为之前优化后的晶胞，计算过程使用的是NPH系综，温度设定在室温(300 K)，积分过程步长时间设定为1fs，总的时间为0.5 ps，迭代步数为1000. Wang[13]研究发现由oP10-FeB4向tP10-FeB4产生相变发生在65.9 GPa，高于65.9 GPa则tP10-FeB4比oP10-FeB4稳定，故计算过程应力值分别设定为70 GPa、100 GPa、150 GPa、200 GPa、250 GPa、300 GPa.

图2为不同应力下对应的tP10-FeB4带隙，从图中可知，随着应力的增加，带隙宽度也会减小，但是减小的幅度会减小.

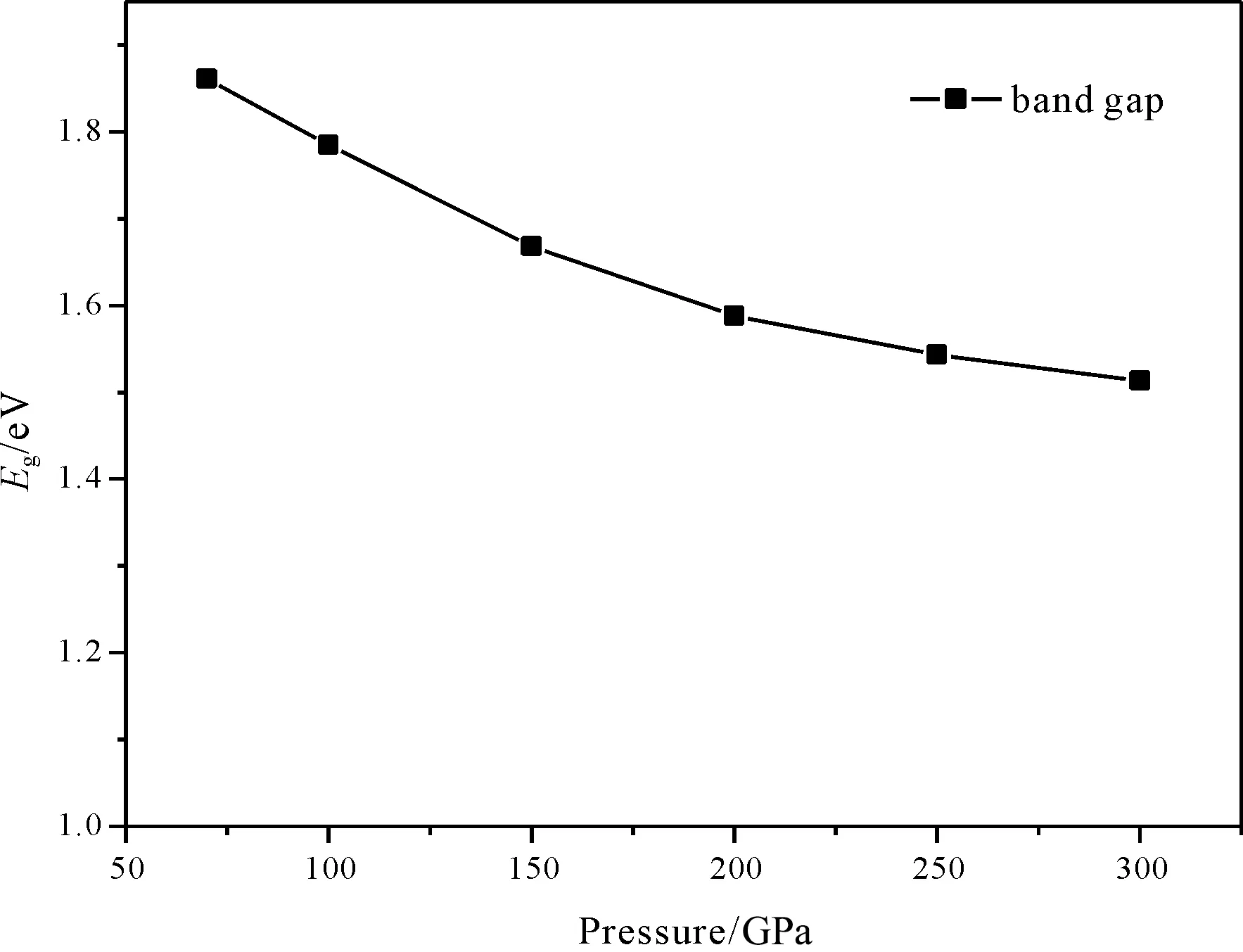
图2 应力对tP10-FeB4带隙的影响Fig. 2 Band gaps of tP10-FeB4 under different pressures

图3为B原子在六种压强下对应的态密度(DOSs)图，从图中可以看出在价带顶附近B原子的p态电子随着压强的增大向低等级移动，导带底部的p态电子也有向低能级移动的趋势. 对应于不同的压强70 GPa、100 GPa、150 GPa、200 GPa、250 GPa、300 GPa，价带顶附近p态电子主要分布在-10.97～0 eV，-11.12～0 eV，-11.35～0 eV，-11.74～0 eV，-12.13～0 eV，-12.52～0 eV区域，s态轨道主要分布于-10.67～0 eV，-10.76～0 eV，-11.37～0 eV，-11.65～0 eV，-12.04～0 eV，-12.42～0 eV区域，因此对于价带而言，随着压强的增大，轨道的弥散性增强、定域性减弱. 这主要是因为压强增大后原子之间的距离减小，因此轨道重叠区域增大，有利于轨道杂化，导致了能带增宽. 另外在价带顶区域，轨道主要是由p态轨道贡献，而远离费米能级的价带主要是由s态轨道贡献. 对于导带而言也具有和价带类似的性质：导带底部随着压强的增大而增宽，定域性减弱，由于导带和价带都增宽，最终导致带隙宽度变窄.

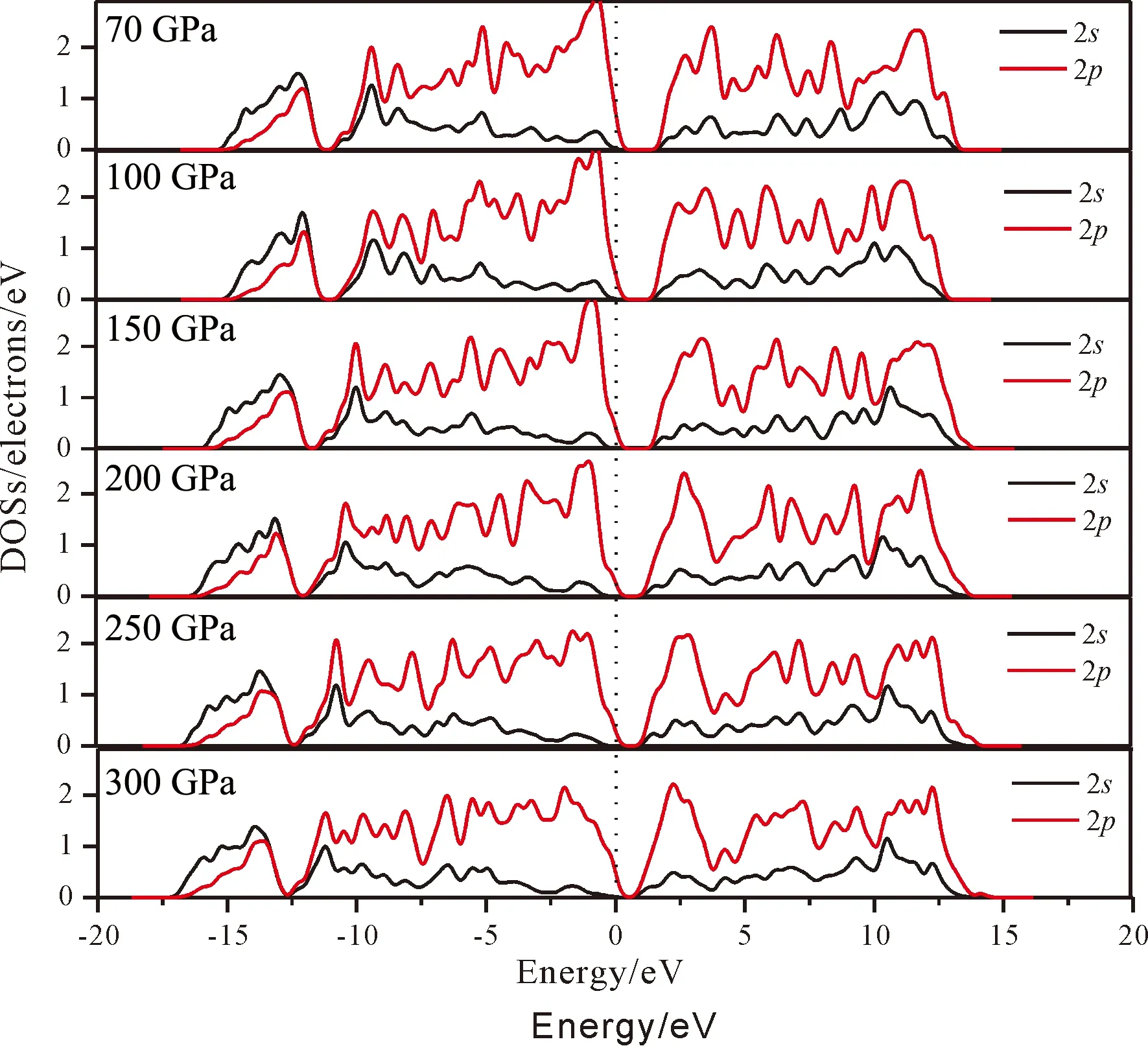
图3 B原子在不同应力下的态密度图Fig. 3 DOSs of B under different pressures

图4为Fe原子在70 GPa、100 GPa、150 GPa、200 GPa、250 GPa、300 GPa下的态密度(DOSs)图，从图中可以看出在价带顶附近Fe原子的d态轨道随着压强的增大向低等级移动. 对应于不同的压强，价带顶附近d态轨道主要分布在-9.66～0 eV，-9.78～0 eV，-10.26～0 eV，-10.65～0 eV，-11.04～0 eV，-11.58～0 eV区域，p态轨道主要分布于-2.37～0 eV，-2.51～0 eV，-2.82～0 eV，-3.48～0 eV，-3.55～0 eV，-3.89～0 eV区域. 价带顶附近的d态波峰随着压强的增大而增宽，分布范围逐步向两侧扩展. 因此对于价带而言，随着压强的增大，轨道的弥散性增强、定域性减弱. 另外在价带顶区域，轨道主要是由d态和p态轨道贡献. 对于导带而言也具有和价带类似的性质：导带底部随着压强的增大也有向低等级移动的趋势，随着压强的增大，能带向两侧扩展、定域性减弱. 最终导致带隙变窄. 最后对比图3和图4发现在费米能级附近，B原子的2p轨道和Fe原子的3d轨道态密度非常相似，所以他们之间存在较强的轨道杂化，而Fe的3d轨道明显强于B原子的2p轨道.

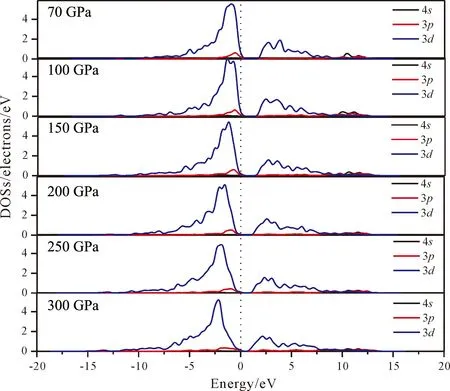
图4 Fe原子在不同应力下的态密度图Fig. 4 DOSs of Fe under different pressures

3.3 应力对tP10-FeB4光学性质的影响

光是电磁波，电磁波在介质中传播时部分会被吸收，为了准确反映光在介质中的传播方程，我们引入了复介电常数方程：

ε(ω)=ε1(ω)+iε2(ω)[24]

该方程能够正确反映能带结构以及固体发光的性质，其中虚部ε2(ω)与能带结构直接相关，描述光子与电子的相互作用情况，实部ε1(ω)则可以通过Kramer-Kronig色散关系[25, 26]由ε2(ω)直接导出. 所有的光学性质包括吸收系数、反射率、折射率等都可以由方程求出来. 但是文中所有的计算都是采用基于密度泛函理论的第一性原理计算得到的，经验已经证明，采用密度泛函理论计算出的能隙的宽度要比实验得出的值小，为了克服这种缺陷，在进行光学性质分析时通常采用剪刀算符对结果进行修正[27, 28]. 我们计算得到的带隙宽度为1.773 eV，而文献中报道的为2.43 eV[14]，因此我们选用0.567 eV为剪刀算符.

图5是通过计算得到的复介电常数的实部(图5a)和虚部(图5b)，从图中可以看出压强由低到高对应的实部和虚部的主要峰值分别位于2.96 eV和4.29 eV，2.816 eV和4.31 eV，2.8 eV和4.4 eV，2.66 eV和4.49 eV处，2.6 eV和4.71 eV处，2.57 eV和4.62 eV处. 结合态密度图可知虚部的最高峰主要源自价带顶的Fe-3d轨道向导带底的B-2p轨道以及Fe-3d轨道跃迁. 另外随着压强的增大，峰值略微减小，这与态密度图中Fe的价带顶3d轨道的变化趋势基本一致. 在虚部6～12 eV范围内还存在几个小的峰值，这也与Fe的导带底3d轨道保存一致. 最后实部曲线的变化规律与虚部的保持一致：在出现最高峰之后迅速下降，之后在6～12 eV范围内出现略微波动. 这也在一定程度上反映了电子的跃迁规律.

为了进一步研究tP10-FeB4的光学性质，我们计算了tP10-FeB4在不同压强下的吸收系数、反射率和折射率. 图6为不同压强下的tP10-FeB4吸收系数，从图中可以看出tP10-FeB4在150 nm开始出现吸收，在200 nm附近迅速达到峰值，这与介电常数虚部的最高峰相对应. 之后在200～320 nm缓慢下降，但是仍然维持在高的水平，波长大于320 nm后吸收系数迅速降低到0. 总体上可以看出在200～320 nm的紫外区间tP10-FeB4有很好的吸收谱，而在可见光区吸收非常小. 对比不同压强对吸收系数的影响发现随着压强的增大，tP10-FeB4吸收的光谱范围增宽，由600 nm扩展到800 nm，这也和带隙宽度随着压强的增大而减小的规律一致. 基于以上的研究，tP10-FeB4可应用于制作高压下的紫外吸收或防护材料.

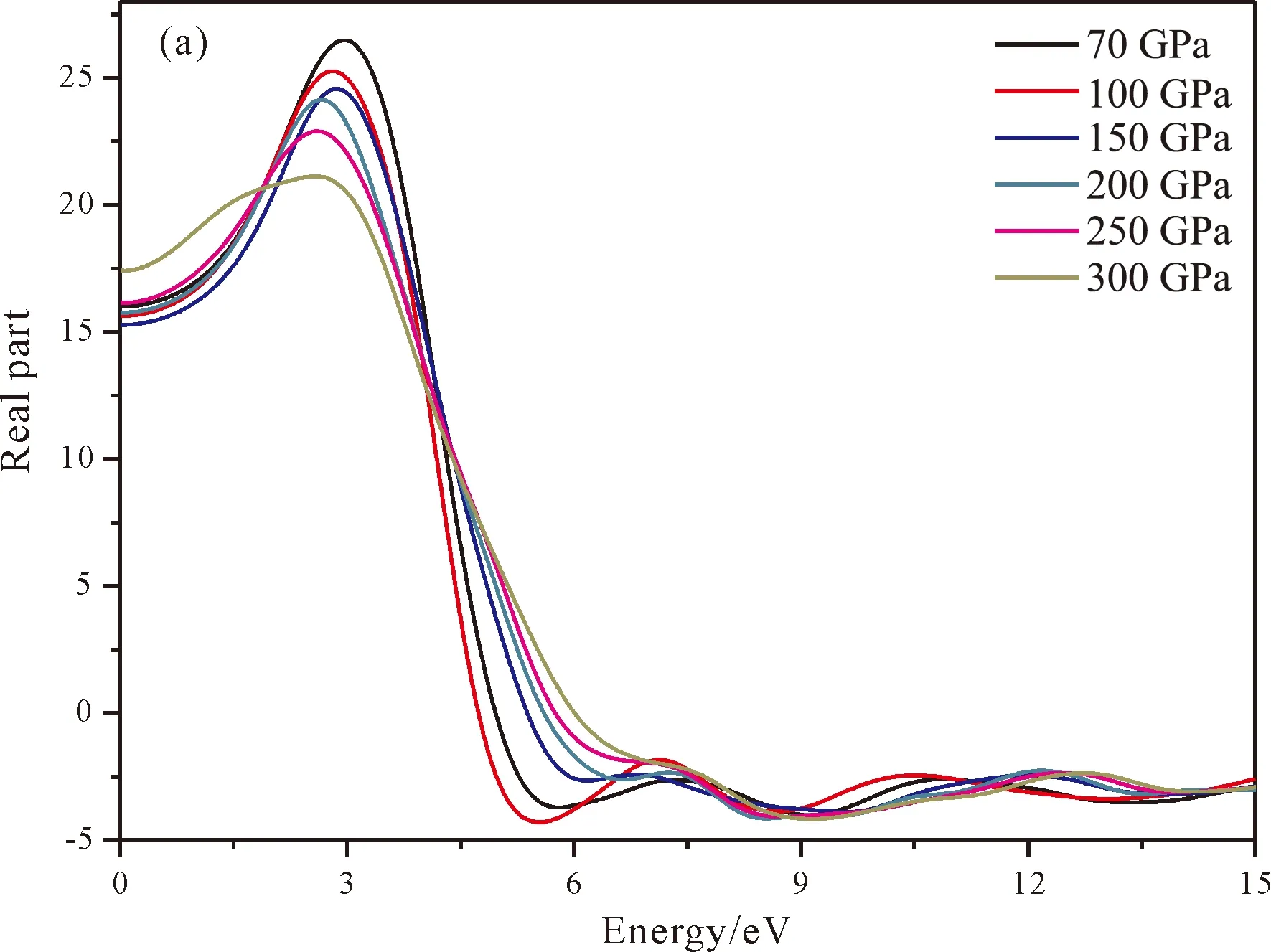
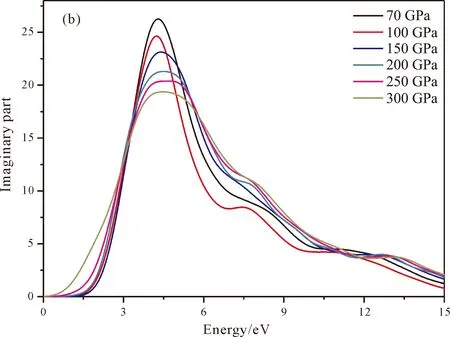
图5 tP10-FeB4复介电常数：(a)实部；(b)虚部Fig. 5 The real part (a) and imaginary part (b) of dielectric function for tP10-FeB4

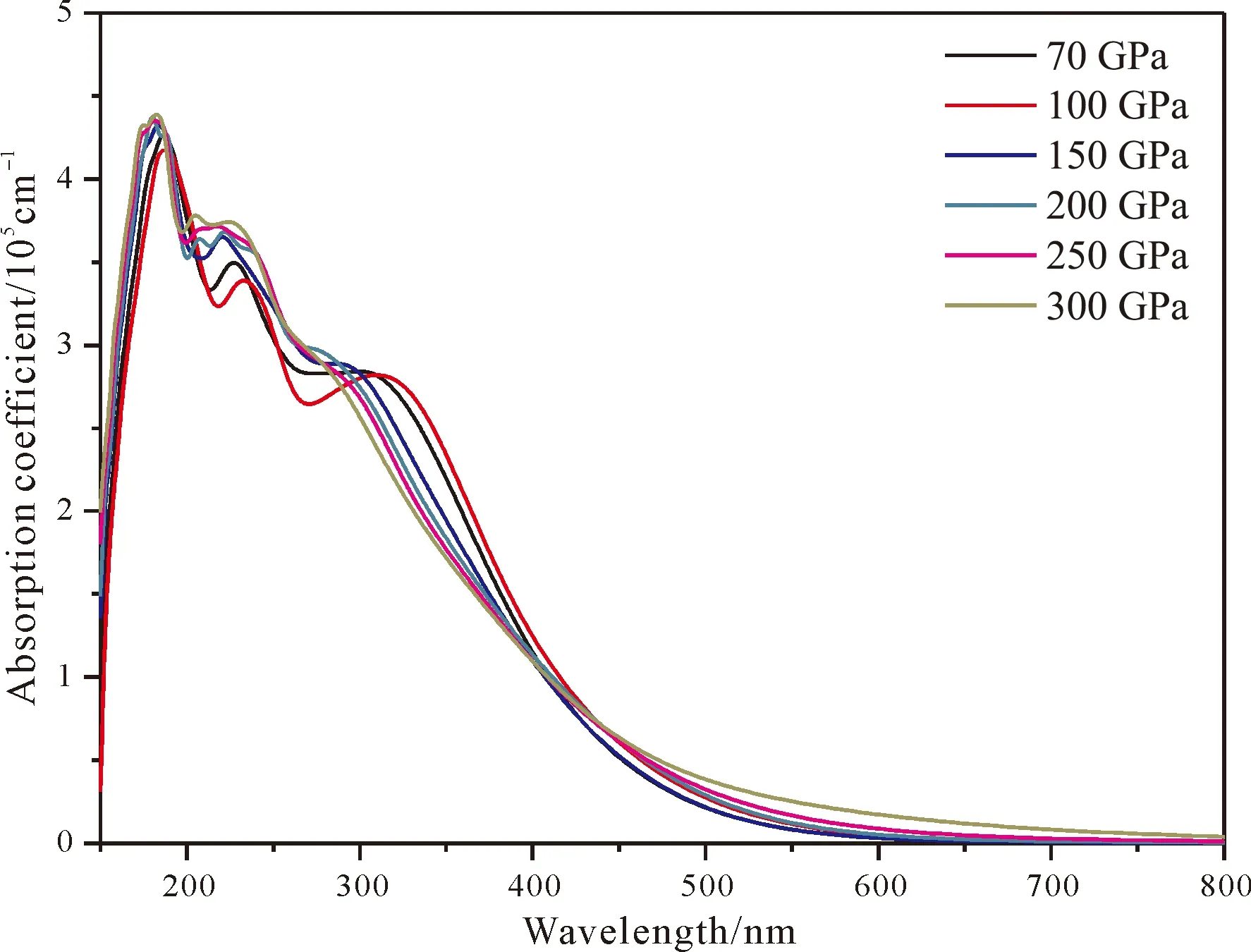
图6 tP10-FeB4吸收系数Fig. 6 The absorption coefficient for tP10-FeB4

图7为不同压强下的tP10-FeB4的反射率，从图中可以看出，在170～400 nm之间的紫外区域反射率大概在0.4～0.5之间波动，而对于可见光区基本维持在0.4左右. 压强对于反射率的影响不是很明显. 图8为tP10-FeB4的折射率，从中可以看出，n在150～400 nm迅速达到一个最高峰，而后缓慢下降，但仍然维持一个高水平状态，因此tP10-FeB4对可见光的折射率比较大，而消光系数k的规律则和复介电常数虚部的性质非常类似：在紫外区域有较强的吸收，而在可见光区吸收较小. 鉴于tP10-FeB4对可见光的折射率比较大且吸收小，因此是潜在用于制作光导纤维的材料.

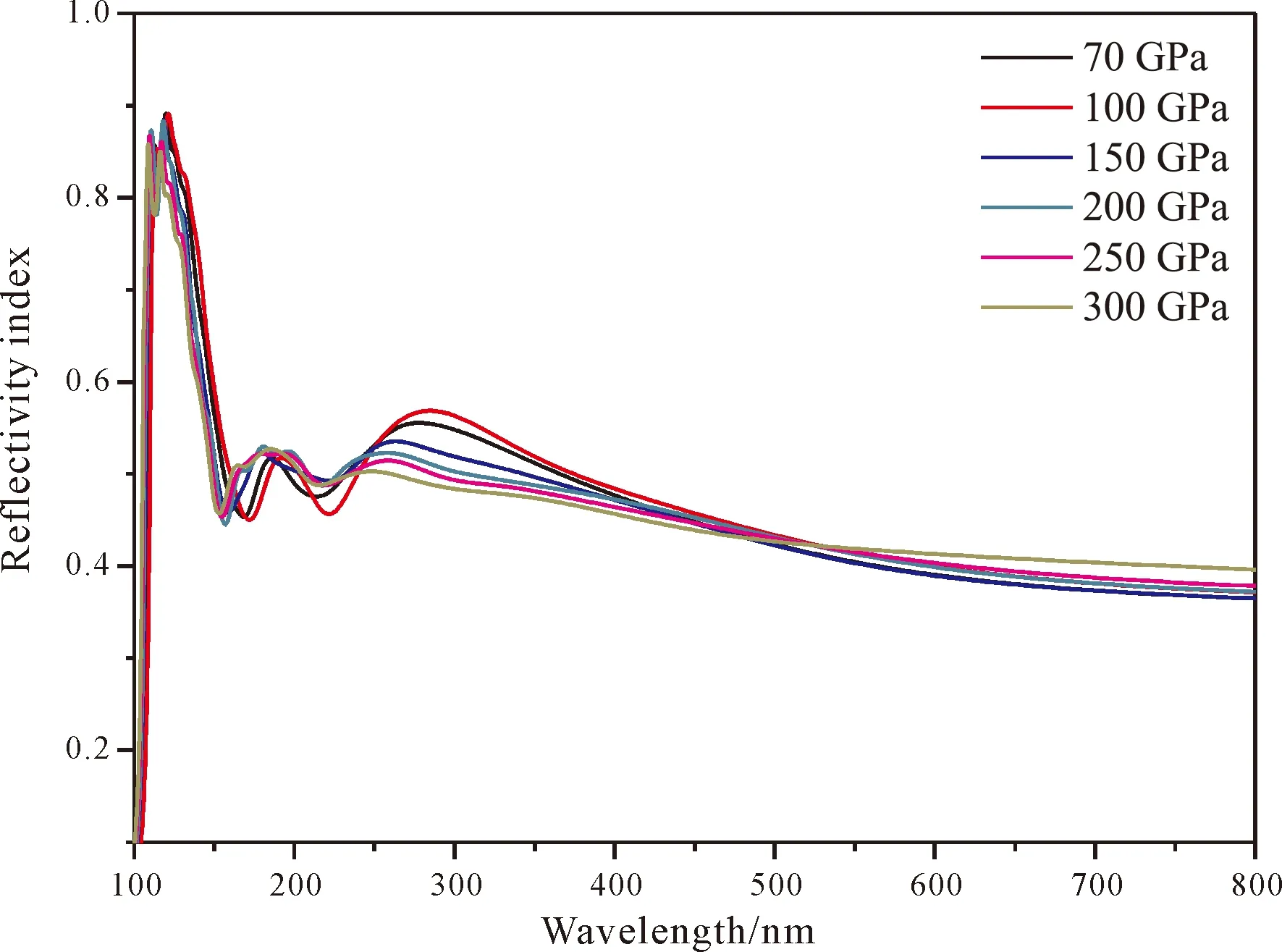
图7 tP10-FeB4的反射率Fig. 7 The reflectivity index for tP10-FeB4

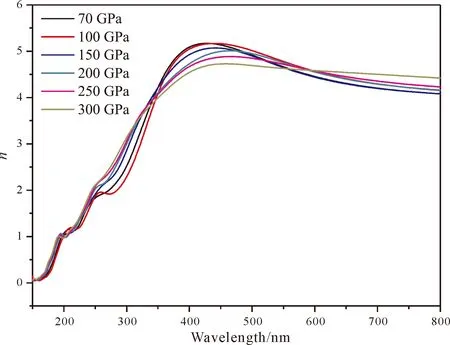
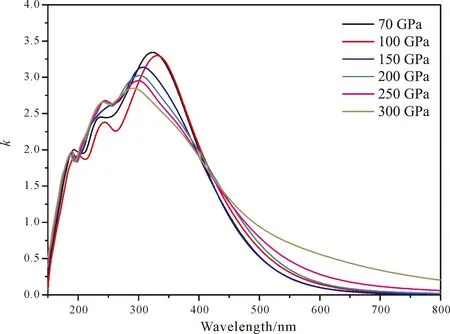
图8 tP10-FeB4的折射率，其中n为实部k为虚部Fig. 8 The refractive index for tP10-FeB4: n is real part and k is imaginary part

4 结 论

本文通过密度泛函理论计算了压强对于tP10-FeB4的电子结构和光学性质的影响，得出了以下几个方面的结论：

1. 随着压强的增大，tP10-FeB4的带隙宽度会减小，所以应力会对tP10-FeB4的带隙产生影响.

2. tP10-FeB4的价带顶部和导带底部主要由Fe的3d、B的2p和2s轨道构成，其中Fe的3d贡献最大. 应力增大后电子的轨道杂化会导致能带宽度变大，压缩带隙的宽度.

3. tP10-FeB4在紫外区间有良好的吸收谱，是潜在的紫外吸收材料. 而在可见光区吸收较小且对可见光的折射率比较大，因此可以考虑用于制作光导纤维.