工程意义上的高斯脉冲信号不失真采样分析*

王云静，张晓林，赵 雷

（北京航空航天大学 电子信息工程学院 北京 100191）

引 言

奈奎斯特采样定理[1]给出了限带信号的不失真采样条件，但目前针对非限带信号采样的讨论较少。通常认为，信号的采样点数越多，抗噪性能越强[2]，恢复误差越小，所以实际应用中对于脉冲信号的采样，为了减小信号的恢复误差，通常会尽可能多地增加采样点数，这对ADC的性能指标提出了很高的要求[3]，进而会大大提高电路的复杂度和硬件成本。

高斯脉冲信号作为一种典型的非限带脉冲信号，广泛存在于核电子学[4]和超宽带通信[5]等领域。本文的研究背景是对一个高斯分布的信号进行采样离散，进而分析误差和离散化参数之间的关系，其本质是研究高斯脉冲采样问题。为了提高研究结果的通用性，本文以一种典型高斯脉冲信号为例，对其采样问题展开分析，基于高斯脉冲信号时-频域特征和ADC采样原理[6]推导出高斯脉冲信号在工程应用下的采样边界条件以及不同采样点下峰值误差达到最小值的概率，为高斯脉冲信号采样问题提供一种工程参考。

1 高斯脉冲信号的时频域特征

1.1 时域特征

高斯脉冲信号通常表示为

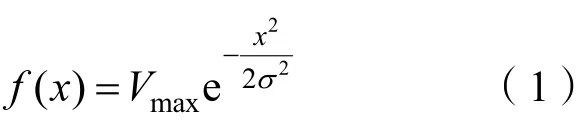
其中，Vmax和σ2分别表示高斯脉冲信号的峰值和方差。

以Vmax=1高斯脉冲信号为例（下文均以此信号为例），用N-bit量化、最大量程与信号最大幅值相等（VADC_max=Vmax）的ADC进行采样，则ADC最小分辨率为。如图1所示，以Δx为采样间隔、M为采样点数，对高斯脉冲信号进行采样，SampleStart和SampleEnd分别是有效采样的起始点和结束点，那么有效数据宽度为

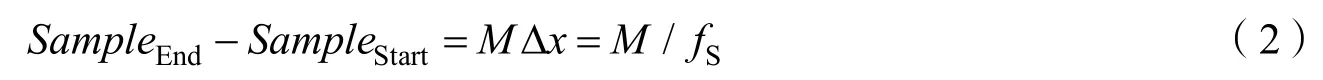
根据ADC量化的原理，只有当采样点处的数据幅值大于等于ADC最小分辨率LSB时，量化数据才大于0。因此，有效采样的起始点和结束点满足

对于有效采样的结束点有

得出有效采样的结束点

由于高斯脉冲信号的对称性，可以得出有效采样的起始点

因此，有效数据宽度为

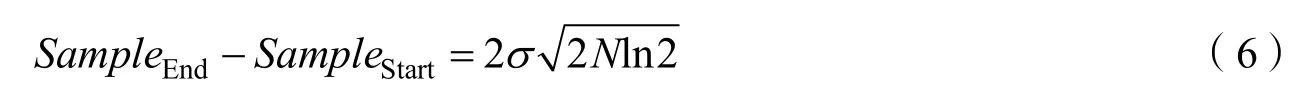
1.2 频域特征

1.2.1 连续高斯脉冲信号的傅里叶变换

连续高斯脉冲信号的傅里叶变换[7]为

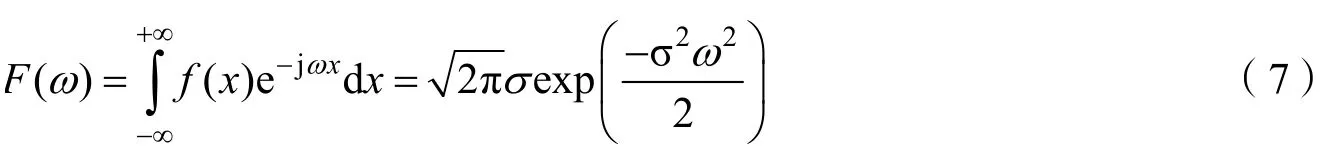
可以看出傅里叶变换后的函数仍为高斯函数，只是幅度和方差发生了变化，如图2所示。

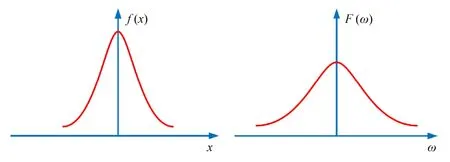
图2 高斯脉冲信号及频谱Fig.2 Gaussian pulse signal and spectrum

1.2.2 离散后的高斯脉冲信号频谱

由傅里叶变换的性质可知，时域离散将导致频域周期延拓[7]，因此以采样频率对连续高斯脉冲信号进行离散后，频谱将以ωS=2πfS为周期进行延拓，如图3。

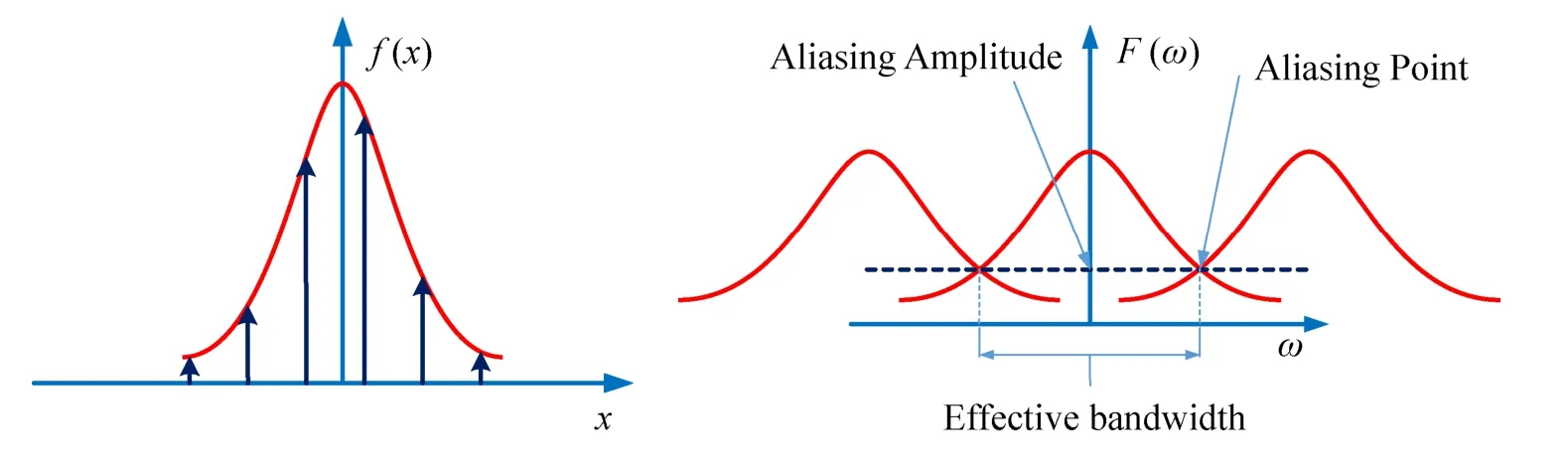
图3 高斯信号采样后的频谱Fig.3 Spectrum of sampled Gaussian signal

1.3 频谱混叠最小的采样条件

由图3可以看出，频谱搬移过程中会发生混叠，混叠点记为0ω，混叠幅度为

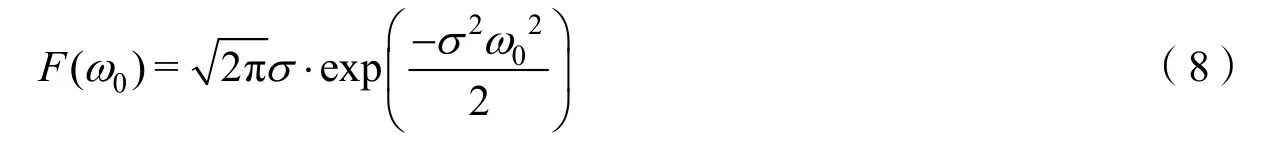
由ADC的采样原理可知，只要混叠高度小于LSB，就认为没有可分辨的混叠进入ADC输出端的采样数据，将对应的采样点数作为高斯脉冲采样的第一个边界条件。因此，混叠幅度需要满足

得到混叠点

这样，根据奈奎斯特采样定理[1]，只要最小采样频率满足

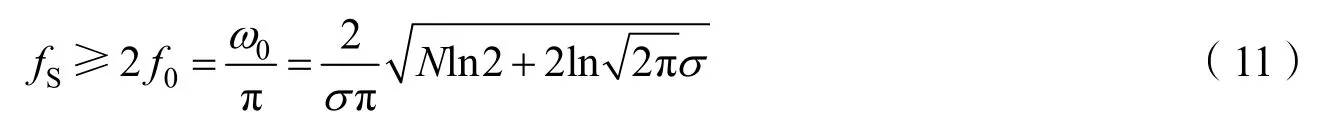
即可认为没有可分辨的混叠进入ADC输出端的采样数据。

因此，频谱混叠最小的采样点数边界为

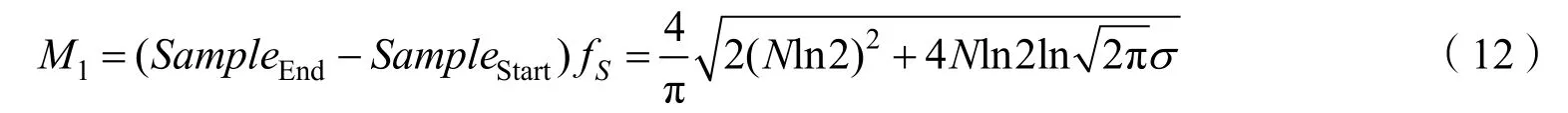
2 峰值误差最小的采样条件

作为一种非周期信号，要保证高斯脉冲信号能够进行工程意义上的不失真恢复的一个重要条件就是要保证其峰值可恢复。对离散数据进行平滑滤波后可得到恢复信号，其峰值不超过离散数据的最大幅度。因此要保证原始信号的峰值可恢复，必须保证采样数据相对原始信号的峰值误差足够小。ADC的最小分辨率为1个LSB，因此ADC输出的量化数据相对于原始信号的峰值误差最小值为1个LSB。

设最靠近峰值点的采样点位置为[k,f(k)]，只要采样数据f(k)相对信号峰值的误差在一个LSB以内，即可保证采样数据f(k)经过量化后能够取到最小峰值误差LSB。则要求

求出临界点为

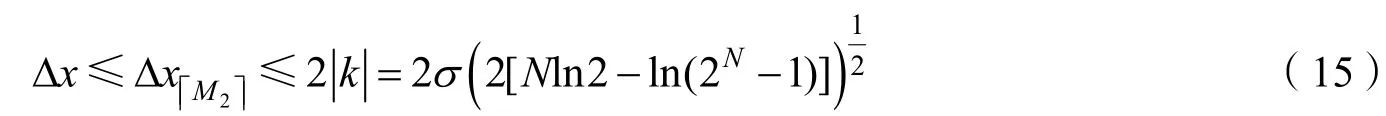
一定能够保证采样数据最大幅度相对于原始信号峰值的误差小于一个LSB，从而保证经过量化后的峰值误差小于ADC的最小分辨率LSB，达到工程意义上的峰值误差最小。

求得使峰值误差最小的采样点数边界为

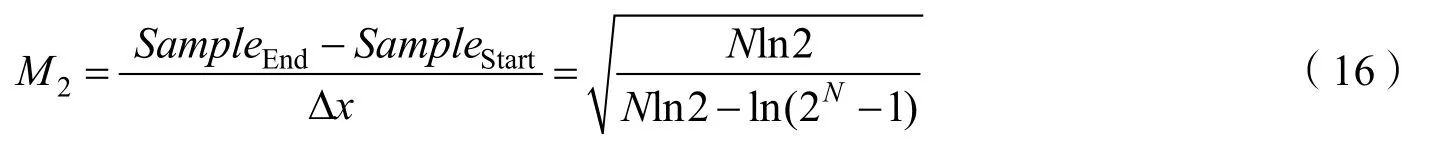
M即为高斯脉冲信号的峰值采样条件。

3 高斯脉冲信号的最小采样点数

以8-bit的ADC为例，对采样点数的两种边界M1和M2进行分析和仿真，结果如图4。

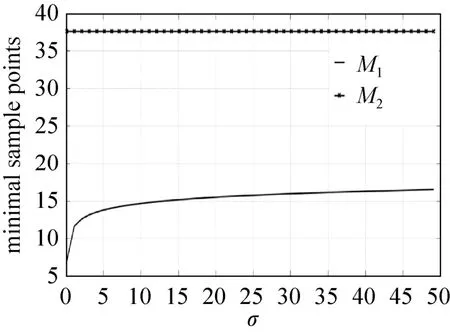
图4 两种边界条件比较Fig.4 Comparison of two boundary conditions

由图4可以看出，在可见范围内，有M1＜M2，而离散数据的频谱混叠小于LSB是高斯脉冲信号采样的最基本条件，因此采样点数至少应该满足M。

4 峰值误差为最小值的概率

4.1 M≥M2时，峰值误差为最小值的概率

因此，当实验次数无穷大时，用频率无限逼近概率[8]，容易得到当采样点数时，峰值误差为最小值的概率等于1。

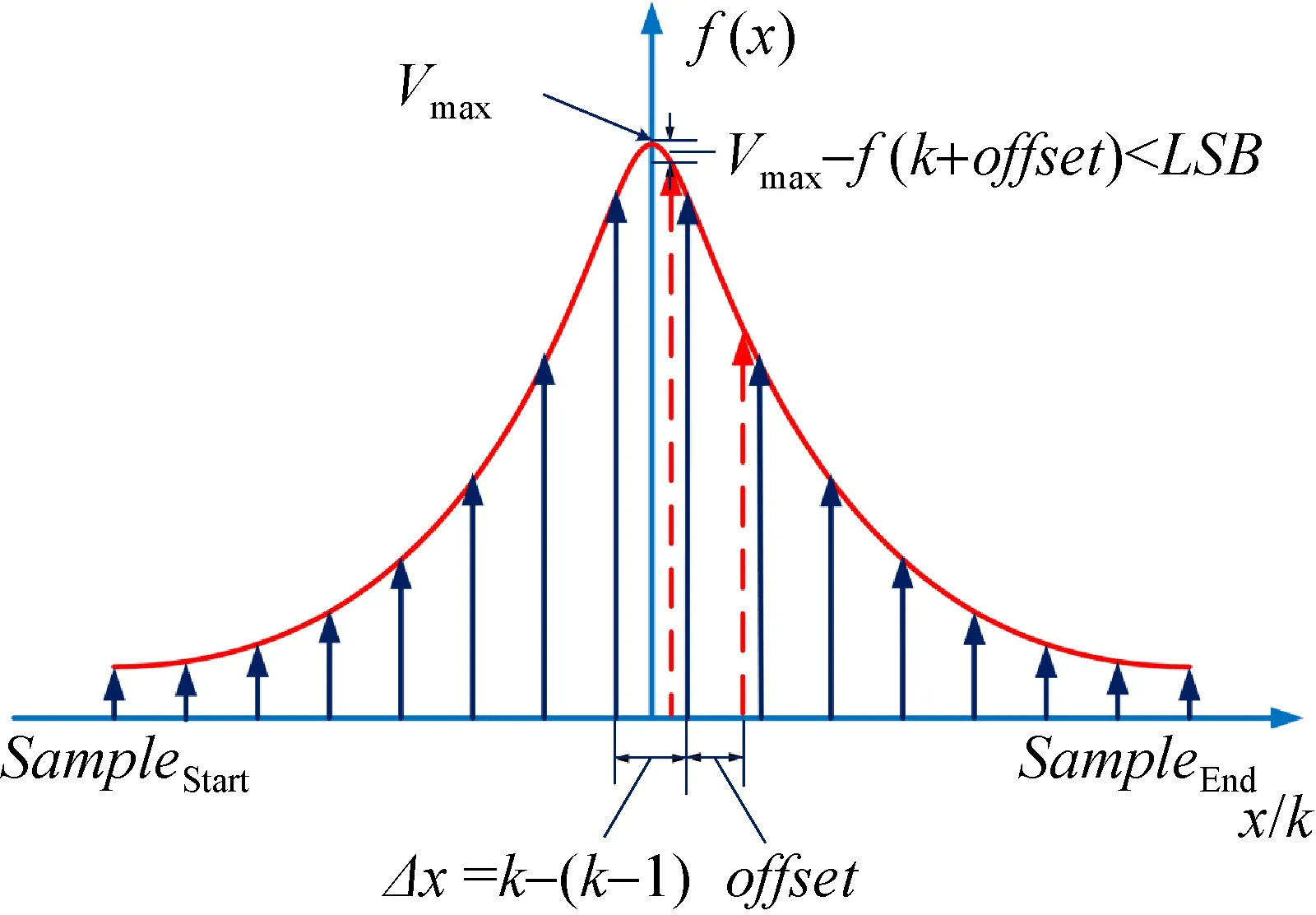
图5 时的峰值误差Fig.5 Peak error when

不同采样点下，峰值误差能够取到最小值的概率问题可以等效为间隔ΔxMx的采样脉冲落在区域的几何概型问题[9]，则不同采样点数对应的峰值误差为最小的概率如式（17）所示。由式（17）可以看出，峰值误差为最小的概率与σ无关。

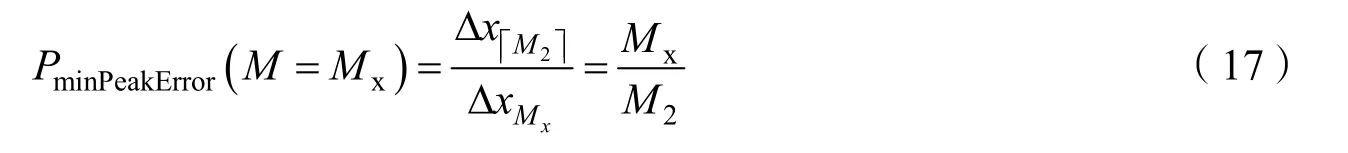
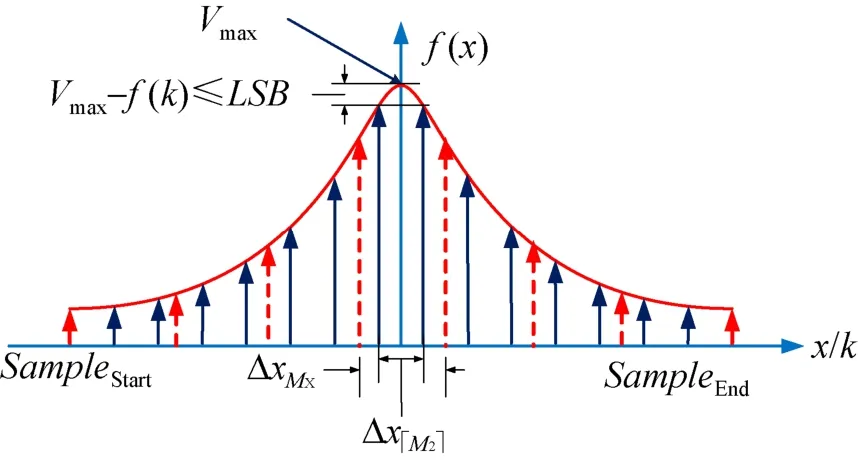
图6 时，峰值误差能够达到最小值的区域Fig.6 The area of the minimum peak error when

5 仿真结果及性能分析

5.1 高斯脉冲信号的采样和恢复仿真

以8-bit的ADC为例，根据式（13）～式（16）的推导，取最小采样点数，对σ=5高斯脉冲信号进行采样和恢复，仿真结果如图7所示。

5.2 峰值误差取到最小值的概率仿真

以8-bit的ADC为例，对σ=5、均值随机变化的高斯脉冲信号采样量化，每次随机试验中都对M进行一次M∈[10,40]的参数扫描，完成105次蒙特卡洛仿真，累计采样数据f(k)的峰值误差小于LSB的次数，最终用采样数据f(k)的峰值误差小于LSB的频率逼近峰值误差能够达到最小值的概率，得到峰值误差能够达到最小值的概率如图8所示。

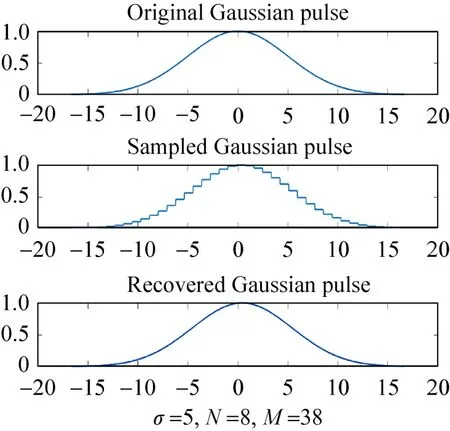
图7 σ=5时的采样和恢复Fig.7 Sampling and recovery of Gaussian signal when σ=5

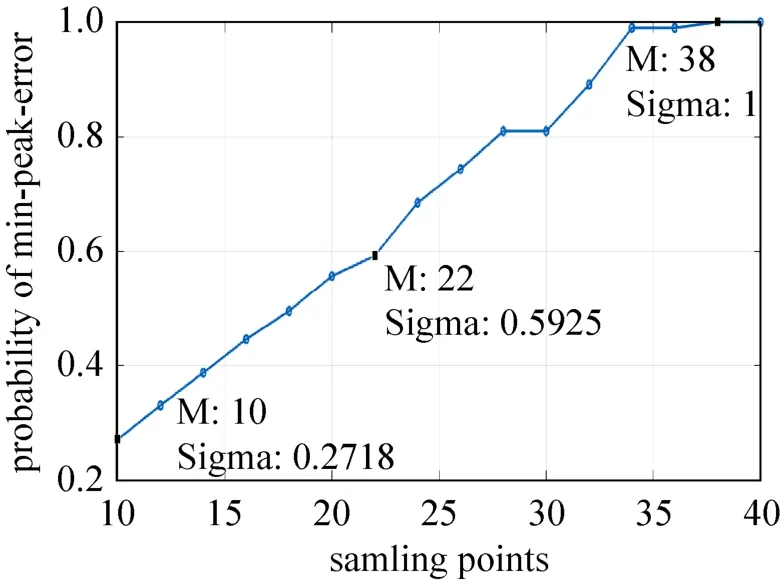
图8 N=8bit时，不同采样点数M下，峰值误差能够取到最小值的概率Fig.8 Probability of the minimum peak error for different sampling points M when N=8 bit

对图8的峰值误差能够达到最小值的概率的仿真数据进行分段拟合，得到概率曲线如图9所示，拟合置信度为95%。

由图8的仿真结果和图9的拟合结果可以看出，采样点数取不同值（记为M=Mx）时，峰值误差能够达到最小值的概率为特殊地，当采样点数时峰值误差为最小值的概率为1，符合式（17）关于峰值误差能够达到最小值的概率的推导结果。

在以上仿真结果的基础上，对σ（σ∈[5,10]，以1为步进）和M（M∈[10,100]，以5为步进）同时进行参数扫描，得到峰值误差能够达到最小值的概率与σ之间的关系，仿真结果如图10所示。可以看出，峰值误差能够达到最小值的概率基本不随σ变化，符合式（17）的理论分析结果。

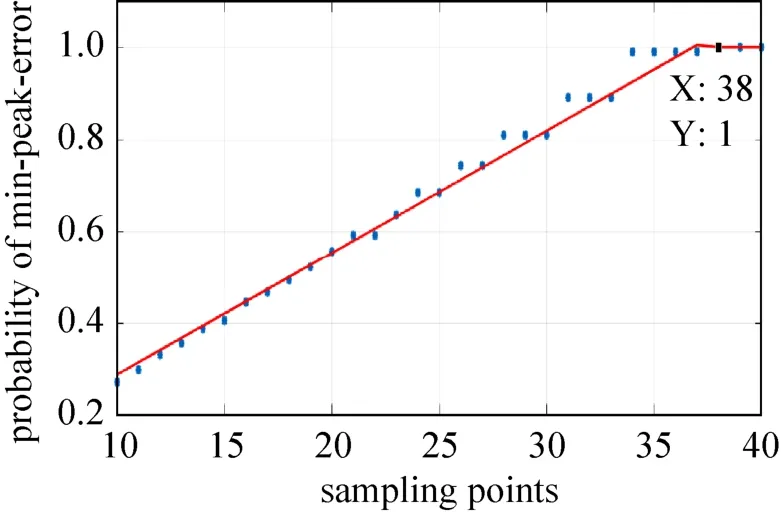
图9 N=8 bit时，拟合得到的峰值误差能够取到最小值的概率曲线Fig.9 The fitting curve of the probability of minimum peak error when N=8 bit

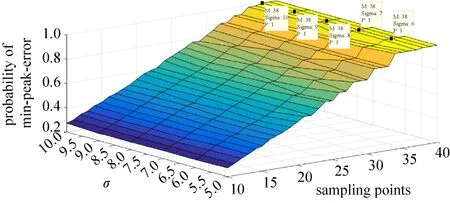
图10 N=8 bit时，对σ和M进行参数扫描，峰值误差能够达到最小值的概率Fig.10 Probability of the minimum peak error for different σ and M when N=8 bit

6 结束语

本文对高斯脉冲信号的采样问题进行讨论，以ADC的原理为基础，对高斯脉冲信号的采样条件进行了分析。分析高斯脉冲信号的时频域特征及其采样的特殊性，推导出高斯脉冲信号的采样条件和不同采样点下的峰值误差能够达到最小值的概率。仿真结果表明，本文基于ADC原理提出的采样条件能够保证高斯脉冲信号以最小误差采样，提出的概率模型能够比较准确地估计不同采样点下峰值误差能够达到最小值的概率，对高斯脉冲信号的采样和重建具有一定的指导意义。