基于时频二维估计的卫星导航失锁快速重定位技术*

张 静，张玉常，张荣兵，孙树杰，董晓明

（1 北京遥测技术研究所 北京 100076；2 火箭军军代室 北京 100076）

引 言

在信号闪断或者弱信号环境下，卫星导航接收机易出现信号失锁现象，无法连续稳定跟踪卫星信号。如何提升接收机的性能，缩短失锁重定位时间，成为卫星导航领域的重要研究方向。

信号失锁后，重定位的时间通常包括信号重新捕获时间、环路建立稳定跟踪时间、位同步时间、帧同步时间和导航解算时间[1]。目前，导航接收机通常采用两种方法来缩短失锁重定位时间：一是辅助捕获方法，利用接收机失锁前的位置、速度和星历信息预报载体的载波多普勒频率，缩小多普勒频率捕获范围，减少重新捕获时间[2,3]；二是利用位置和星历信息反推卫星信号当前时刻的位计数和帧计数，省去位同步和帧同步时间[4,5]。这两种方法均依赖于载体位置和星历信息，且方法一由于没有预报码相位，仍需进行信号捕获，方法二存在进位模糊度问题，因此应用具有局限性。

本文提出一条新思路，认为在信号失锁之前接收机稳定跟踪信号期间获得的载波多普勒频率、码多普勒频率和码相位等信息仍具有可用价值，依据这些先验信息不仅可以估计当前时刻信号的载波多普勒频率，而且可以准确估计位计数、帧计数和码相位，以此来实现快速重定位。相对而言，此方法不需要占用捕获模块，各个跟踪模块可并行工作，进一步缩短重定位时间，且它不依赖载体位置和星历信息，应用更为广泛。

1 基于时频二维估计的重定位技术

信号失锁后，接收机的常规处理是启用信号捕获功能，对载波多普勒频率和码相位进行大范围的二维搜索（如图1（a）所示），并需要重新进行位同步和帧同步以获得准确的历元观测值，这种方法适用于信号失锁时间长或者载体动态变化较大的应用场景[6,7]。

对于中低动态的应用场景，如果能准确预估信号恢复后的载波多普勒频率和码相位，使其在环路的牵引范围内，无需信号重新捕获即可直接转跟踪处理（如图1（b）所示），这样一来可省去位同步和帧同步过程，重定位的时间只包括环路建立稳定跟踪时间和导航解算时间，相比常规处理将大大缩短。

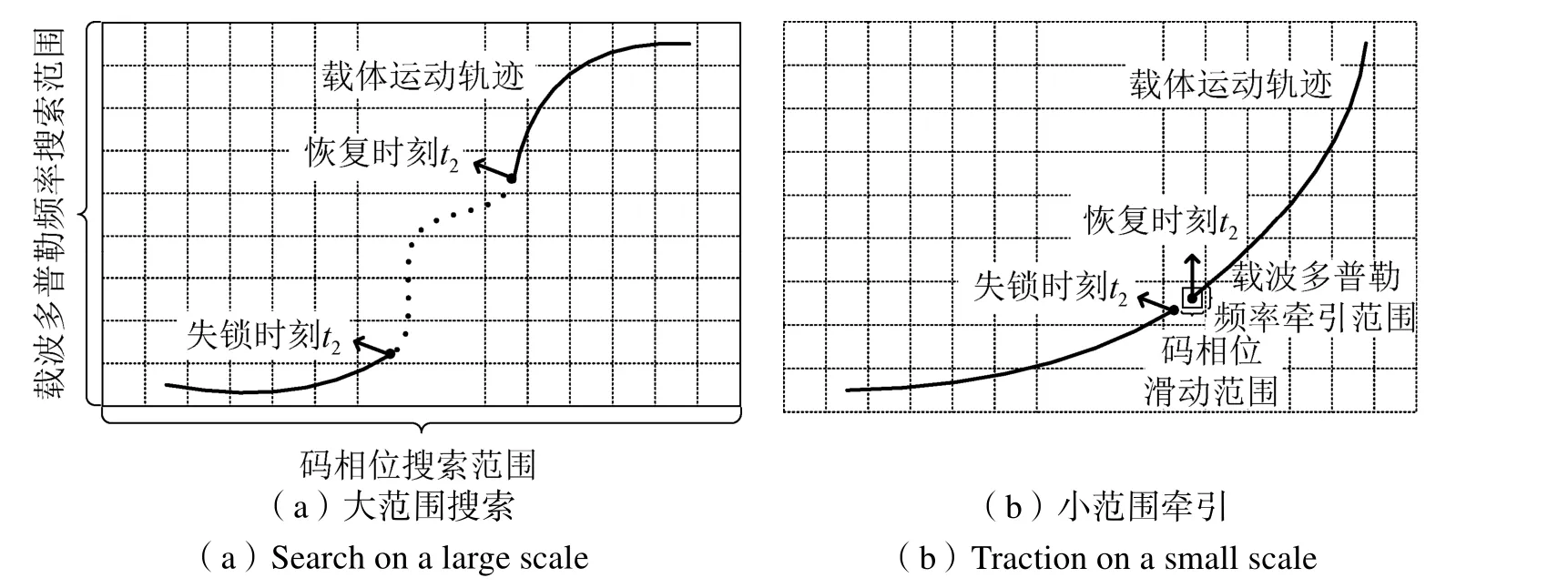
图1 信号捕获二维搜索示意图Fig.1 Two-dimensional search in signal capture

基于以上思路，本文提出一种基于时频二维估计的卫星导航信号失锁快速重定位技术。对于中低动态的应用场景，通过分析卫星载波多普勒频率的变化趋势，可知其载波多普勒频率近似呈线性变化，车载和机载应用中卫星多普勒频率变化曲线如图2所示。

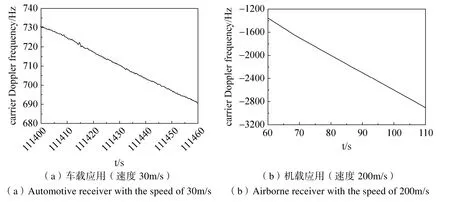
图2 中低动态场景下卫星载波多普勒频率的变化曲线Fig.2 Satellite carrier Doppler frequency in low and middle dynamic scene

据此提出基于时频二维的估计算法：首先依据信号失锁之前接收机获得的载波多普勒频率和码相位等先验信息，通过线性拟合的方式建立模型；然后预估信号恢复后的多普勒频率和码相位，缩小其不确定范围，保证预估多普勒频率和码相位在接收机环路的牵引范围内，这样无需经过信号捕获阶段就能直接转跟踪处理；待稳定跟踪后也无需进行位同步和帧同步，即可进行导航解算，实现信号恢复后的快速重定位。

基于时频二维估计算法的数据流如图3所示。先验信息包括本地时间和时钟钟漂值、失锁前载波和码多普勒频率测量值、伪码基准速率及失锁前码相位测量值，经过估算后得到信号恢复后的载波和码NCO频率控制字、码相位、码历元值和码启动点，用于信号跟踪和导航解算。

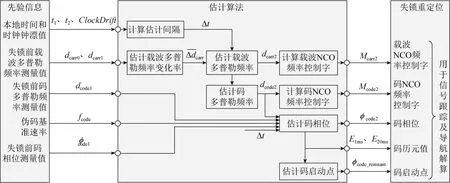
图3 基于时频二维估计算法的数据流图Fig.3 The data flow of time-frequency estimation based algorithm

图3中基于时频二维估计算法的核心是建立数学模型估计载波多普勒频率的平均变化率，以此为基础对其余信息进行估计。下面以一颗卫星为例对基于时频二维估计算法的详细步骤进行描述。

步骤1 计算估计间隔

信号失锁时接收机本地时间为t1，信号恢复时本地时间为t2。本地时间由本地时钟产生，因此估计间隔受时钟钟漂的影响。由于短时间内钟漂变化相对平稳，因此可使用失锁前接收机定位解算得到的时钟钟漂对估计间隔进行计算。估计间隔Δt的计算公式为：

其中ClockDrift表示接收机的时钟钟漂。

步骤2 估计载波多普勒频率

对载波多普勒频率进行一次线性拟合，建立模型，如图4所示。

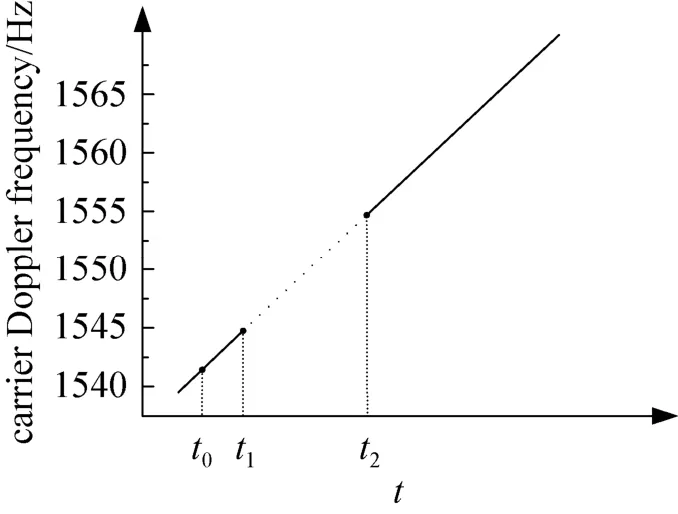
图4 载波多普勒频率近似拟合曲线Fig.4 Approximate fitting curve of carrier Doppler frequency

设卫星信号失锁前t0时刻接收机跟踪获得的载波多普勒频率为dcarr0，t1时刻跟踪获得的载波多普勒频率为dcarr1，则载波多普勒频率变化率的平均值用式（2）计算。

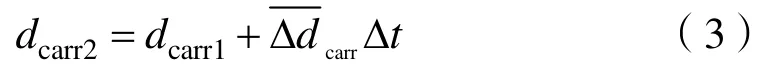
步骤3 估计码多普勒频率

t2时刻的码多普勒频率可以通过式（4）计算得到。

其中，fcode表示伪码基准速率，单位为chip/s，fcarr表示载波基准频率，单位为Hz。

步骤4 估计码相位

t2时刻的码相位为失锁前t1时刻的码相位与码相位变化量之和，其中码相位变化量等于估计间隔内码速率（码基准速率+码多普勒频率）与时间轴围成的梯形面积，如图5所示。t2时刻的码相位计算公式如式（5）所示。

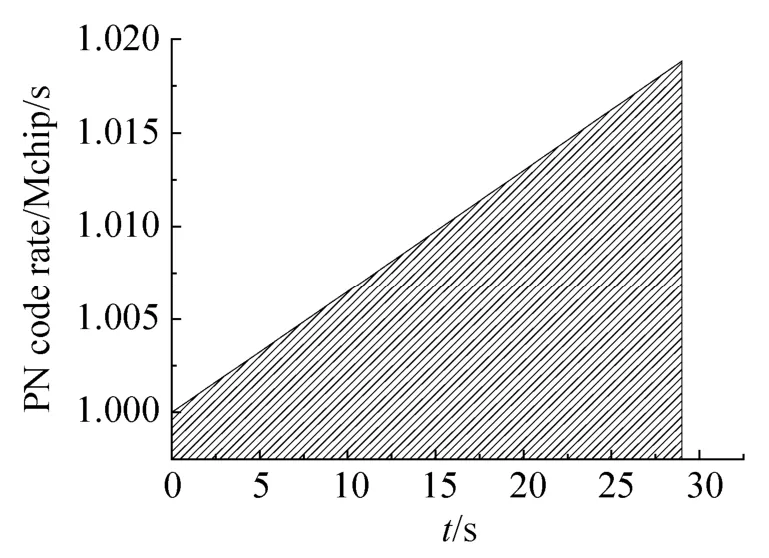
图5 码相位变化量示意图Fig.5 PN code phase variation

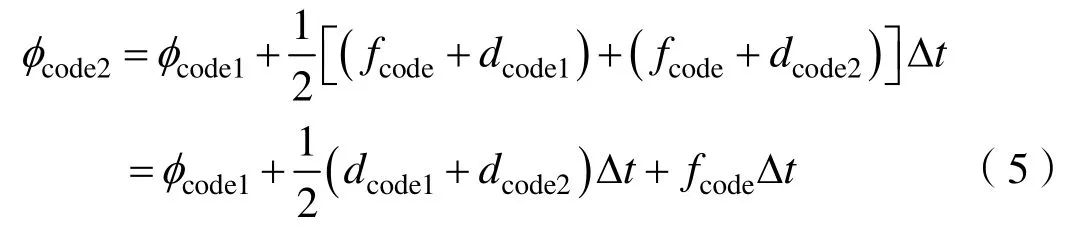
其中，φcode1表示失锁前t1时刻码相位，dcode1表示失锁前t1时刻码多普勒频率。

步骤5 计算载波NCO和码NCO频率控制字

载波和码跟踪环使用数字控制振荡器（NCO）复现载波频率和伪码速率，可通过式（6）计算频率控制字[8]。

其中，f表示载波频率或码速率，N表示NCO保持寄存器长度，fs表示NCO的工作时钟。

步骤6 估计码启动点

依据步骤4中t2时刻码相位的估计结果，可知t2时刻距第一个积分起点的码相位差φcode_remnant，即得出码启动点（积分起点），此时启动码的生成，转跟踪处理。

步骤7 估计码历元值

依据t2时刻码相位的估计结果，可得到信号恢复后码1ms历元值E1ms和20ms历元值E20ms，用于导航解算。

2 误差分析

本文提出的快速重定位技术中，先验信息中存在测量误差的包括失锁前载波多普勒频率测量值、失锁前码多普勒频率测量值、失锁前码相位测量值和时钟钟漂值，常规接收机中各个先验信息的测量误差如表1所示。

表1 先验信息测量误差Table 1 Measurement error of prior information

下面依据先验信息的测量误差最大值对载波多普勒频率、码多普勒频率和码相位的估计误差进行分析。

2.1 载波多普勒频率估计误差

通过分析载波多普勒频率平均变化率的估计公式（2），可以得到的误差范围如式（7）所示。

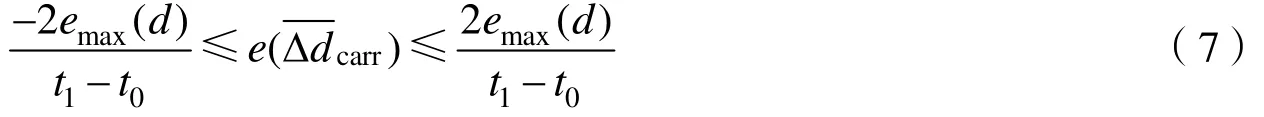
其中emax(d)表示载波多普勒频率单次测量误差绝对值的最大值，此处为1Hz。

依据工程经验，时长t1-t0取值为6s，则的范围为考虑失锁前载波多普勒频率本身的测量误差范围为[–1,1]Hz，由式（3）可得不同失锁时间载波多普勒频率误差绝对值的最大值，如表2所示。

表2 不同失锁时间载波多普勒频率误差绝对值的最大值Table 2 The maximum carrier Doppler frequency absolute error

从表2可以看出，采用本文提出的快速重定位技术，当失锁时间在60s以内时载波多普勒频率的估计误差在锁频环的牵引范围内。

2.2 码多普勒频率估计误差

码多普勒频率估计误差与载波多普勒频率估计误差成比例关系，按照式（4）计算可得出不同失锁时间码多普勒频率误差绝对值的最大值。经计算，当失锁时间在60s以内时，估计误差均在伪码滑动范围内。

2.3 码相位估计误差

从式（5）可知，码相位估计误差由失锁前码相位测量误差和码相位变化量的估计误差共同决定。其中码相位变化量的估计误差由失锁前码多普勒频率测量误差、码多普勒频率估计误差、时钟钟漂决定。码相位变化量的估计误差存在以下四种情况，如图6所示。

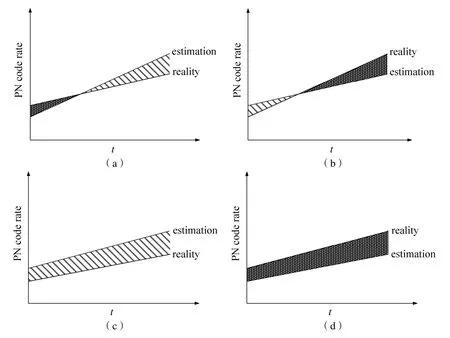
图6 码相位变化量估计误差示意图Fig.6 The evaluation error of PN code phase variation

①图6（a）中，失锁前码速率测量值低于真值，失锁后码速率估计值高于真值；图6（b）中，失锁前码速率测量值高于真值，失锁后码速率估计值低于真值；这两种情况下码相位变化量的估计误差都等于图中画斜线的阴影面积减去画点的阴影面积。

②图6（c）中，失锁前码速率测量值高于真值，且码速率估计值始终高于真值，码相位变化量的估计误差为画斜线的阴影面积。

③图6（d）中，失锁前码速率测量值低于真值，且码速率估计值始终低于真值，码相位变化量的估计误差为画点的阴影面积。

通过比较图6四种情况可知，图6（c）和图6（d）所示的码相位变化量估计误差最大。

码相位变化量估计误差与失锁前码相位测量误差（优于0.01chip）相加，即可计算出不同系统频点码相位估计误差绝对值的最大值，如表3所示。

由表3可以看出，对于GPS-L1、GLONASS-G1和BDS-B1信号，伪码基准速率越大，失锁时间越长，则码相位估计误差越大。当失锁时间在60s以内时，三系统频点的码相位估计误差均在转跟踪滑动范围内。

表3 码相位估计误差绝对值的最大值（单位：chip）Table 3 The maximum evaluation absolute error of PN code phase（unit:chip）

3 工程实现及试验验证

本文基于一款GPS-L1、GLONASS-G1、BDS-B1多系统导航接收机进行失锁快速重定位技术的工程实现及试验验证。接收机软件由基带处理软件和导航应用软件组成，基带处理软件完成信号的预处理、捕获、跟踪和观测量提取，输出伪距、伪距变化率、时间、电文给导航应用软件，由导航应用软件进行导航解算，得出时间、位置、速度等信息。

3.1 工程实现

在原有软件处理流程基础上嵌入本文提出的算法，在接收机跟踪的某颗卫星信号出现失锁后，按照第1节中步骤对该颗卫星信号的载波多普勒频率、码多普勒频率和码相位等信息进行预估并重新启动跟踪，其工程实现的软件流程如图7所示。当卫星跟踪状态达到码同步、载波同步后即可参与定位，实现失锁快速重定位。

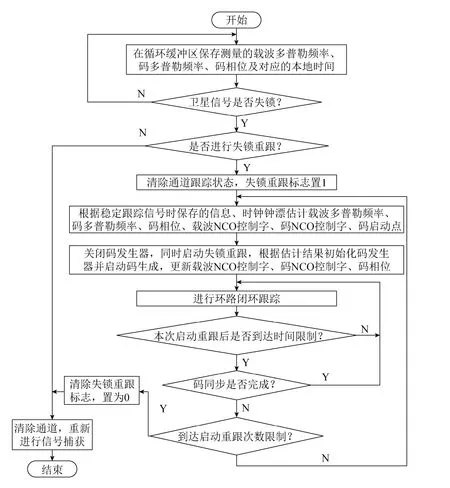
图7 算法工程实现软件流程Fig.7 The algorithm flow chart

3.2 试验验证

为了验证本技术的工程实现效果，使用卫星信号模拟器在车载（速度最大为30m/s，加速度最大为0.3g）和机载（速度最大为200m/s，加速度最大为3g）应用场景下对GPS-L1、GLONASS-G1和BDS-B1三系统频点进行了收星定位试验，测试框图如图8所示，具体测试情况如下所述。

首先测试本算法的估计误差。接收机开机定位解算出时钟钟漂后，设置跟踪通道启用时频二维估计算法，但信号保持正常跟踪，通过比对实际跟踪与估计的载波多普勒频率及码相位差值得到估计误差。

估计误差如表4所示，表中数据为多次测试的统计RMS结果。以GPS-L1系统为例，估计的载波多普勒频率减去实际跟踪的载波多普勒频率得到多普勒频率估计误差，如图9所示，估计的码相位减去实际跟踪的码相位得到码相位估计误差，如图10所示。

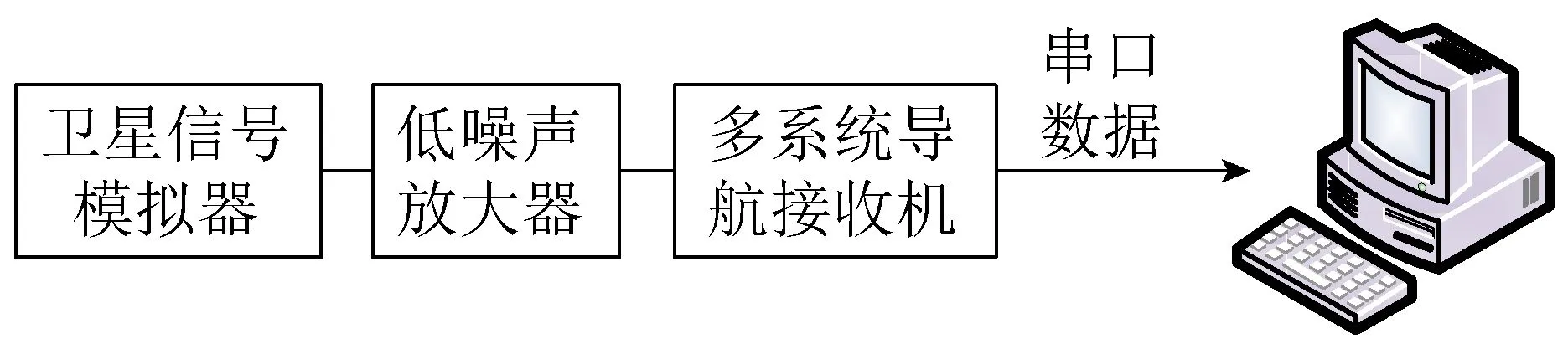
图8 测试框图Fig.8 Test diagram

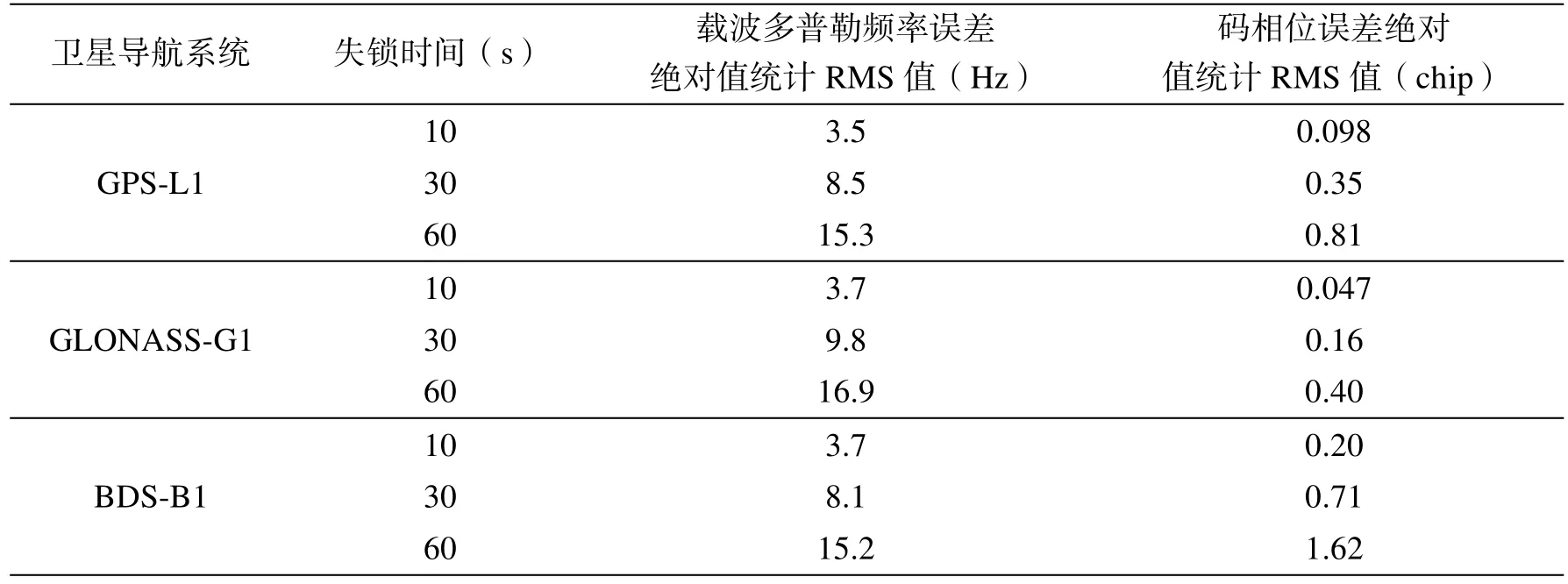
表4 载波多普勒频率与码相位估计误差测量值Table 4 The measured evaluation errors of carrier Doppler frequency and PN code phase

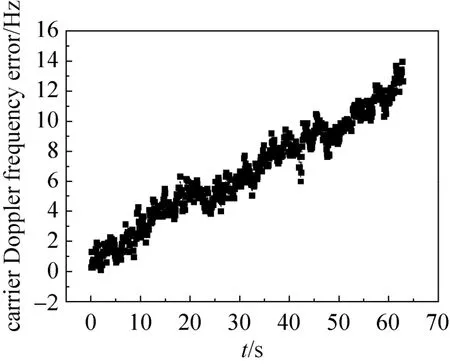
图9 载波多普勒频率估计误差Fig.9 The evaluation error of carrier Doppler frequency

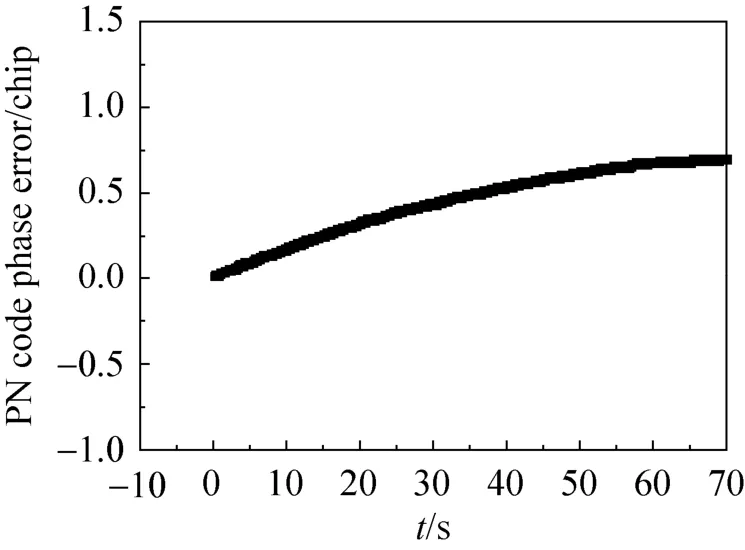
图10 码相位估计误差Fig.10 The evaluation error of PN code phase

在弱信号环境下，测试各系统信号失锁恢复后接收机的跟踪情况及重定位时间。采用高灵敏度跟踪，跟踪环路积分时间设为10ms。接收机开机定位解算出时钟钟漂后，调节接收机信号输入功率，关闭卫星信号后再打开信号，观察在不同输入功率下信号跟踪情况并记录接收机重定位的时间。

测试结果表明，在信号输入功率高于–145dBm、信号失锁时间小于60s时，信号恢复后接收机能够实现对所有可见卫星信号的稳定跟踪，在1s内实现重定位，位置、速度误差在精度范围内，测试结果如表5所示。

表5 失锁重定位时间及位置、速度误差Table 5 Test results of repositioning time and errors of position and speed

4 结束语

本文提出一种基于时频二维估计的卫星导航失锁快速重定位技术，并基于一款多系统导航接收机进行了工程实现及试验验证。试验结果表明，基于时频二维估计的载波多普勒频率和码相位估计误差在理论分析范围内，估计精度满足快速重定位的要求；在信号输入功率高于–145dBm（积分时间为10ms）、信号失锁时间小于60s时，接收机失锁重定位时间在1s以内，较常规信号重捕大大缩短，适用于中低动态场景的接收机。