基于广义互相关算法的遥测时延提取方法研究*

刘 颖，吕彦东，孙志成，张 娜，付庆勇

（中国人民解放军63850部队 白城 137000）

引 言

遥测、雷达和光学设备联合应用，一直是靶场测量导弹飞行参数的技术方法。随着远程制导武器的迅猛发展，导弹、火箭弹等弹载遥测数据中普遍包含GNSS信息，遥测技术的应用得到进一步拓展，可以对弹丸进行全程跟踪，解算弹道数据并引导其他参试设备。但目前基于遥测设备的弹道测量存在一定时延，出现测量弹道滞后现象，导致对其他设备进行引导时精度不足，而如何提取时延并对弹道进行修正是亟需解决的问题[1-3]。时延主要包括弹上设备时延、空中传输时延以及地面站数据处理时延三种，目前研究多是对单一的时延进行分析和计算，本文则是将其视为一个整体进行计算和修正，提出一种利用信号的广义互相关函数计算时间延迟的方法，具有计算量小、噪声抑制效果明显等优势[4,5]。本文方法以雷达弹道数据为参考值，利用广义互相关原理提取遥测弹道时延，在对遥测数据预处理的基础上，建立广义互相关模型，计算互相关函数，并对遥测弹道进行修正，提高遥测设备弹道测量精度。

1 利用广义互相关算法计算时延值

无论是遥测GNSS弹道数据还是雷达弹道数据，都可以写成真实弹道与误差（包括随机误差和系统误差）之和的形式。遥测弹道数据和雷达弹道数据可以分别写成

其中，x1(t)和x2(t)分别为遥测和雷达弹道某测向测量数据，x(t)为真实弹道，n1(t)和n2(t)分别为遥测和雷达弹道测量数据的误差。D即为遥测弹道时延。

互相关时延估计算法基本原理如下，互相关函数定义为：

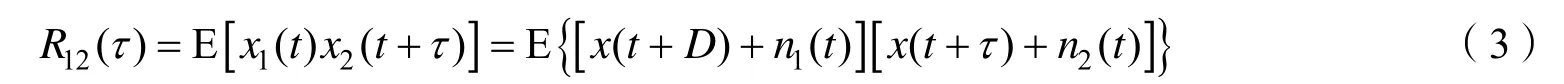
因为x(t)、n1(t)、n2(t)互不相关，式（3）简化为

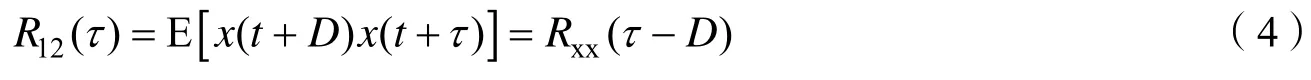
由互相关函数性质

可知，当τ=D时Rxx(τ-D)达到最大值，两个函数相关性最大，即R12(τ)取得最大值时，τ值即为时延。

传统的互相关时延估计算法计算简单、直观，但互相关函数受原始信号谱和噪声的影响具有不稳定性，导致计算所得相关函数峰值不够尖锐，时延误差大、不精确。本文利用广义互相关算法进行时延求解，通过求两信号之间的互功率谱，并在频域内给予一定的加权来抑制噪声的影响，再反变换到时域，从而得到两信号之间的互相关函数，这样一来互相关函数峰值尖锐，其位置则对应于两信号之间的相对时延。

在广义互相关算法中，由维纳-辛钦定理，广义互相关函数与互功率谱函数构成傅里叶变化关系，广义互相关函数模型定义为：

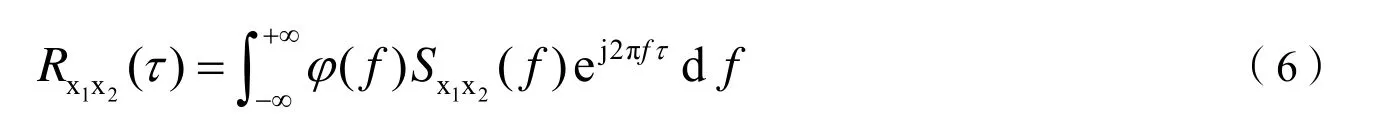
其中，Rx1x2(τ)为广义互相关函数，φ(f)为互功率谱加权函数，可抑制信道噪声，Sx1x2(f)为两信号的互功率谱估计，有

其中，X1(f)和X2(f)为信号x1(t)和x2(t)的自谱。

当信号为离散序列时，若稳定序列x(n)和y(n)具有足够相关性，则所得互相关序列绝对值最大的元素对应的偏差值与数据采样频率的乘积即为x(n)相对于y(n)的滞后时间。

2 仿真计算与结果分析

为了验证本文算法的可行性与可靠性，以正弦函数y=sin(x)为例，对提出的方法进行仿真验证。取由于仿真数据不存在随机误差与漂移误差，所以不需要预处理，根据函数性质理论时延值为0.25。利用互相关性计算得到的x(t)与y(t)的互相关序列估计值如图1所示，可以看出最大值出现在τ=250，乘以采样频率1ms，计算所得的时延值为0.25，证明理想模型下本算法能够计算出准确的时延值。

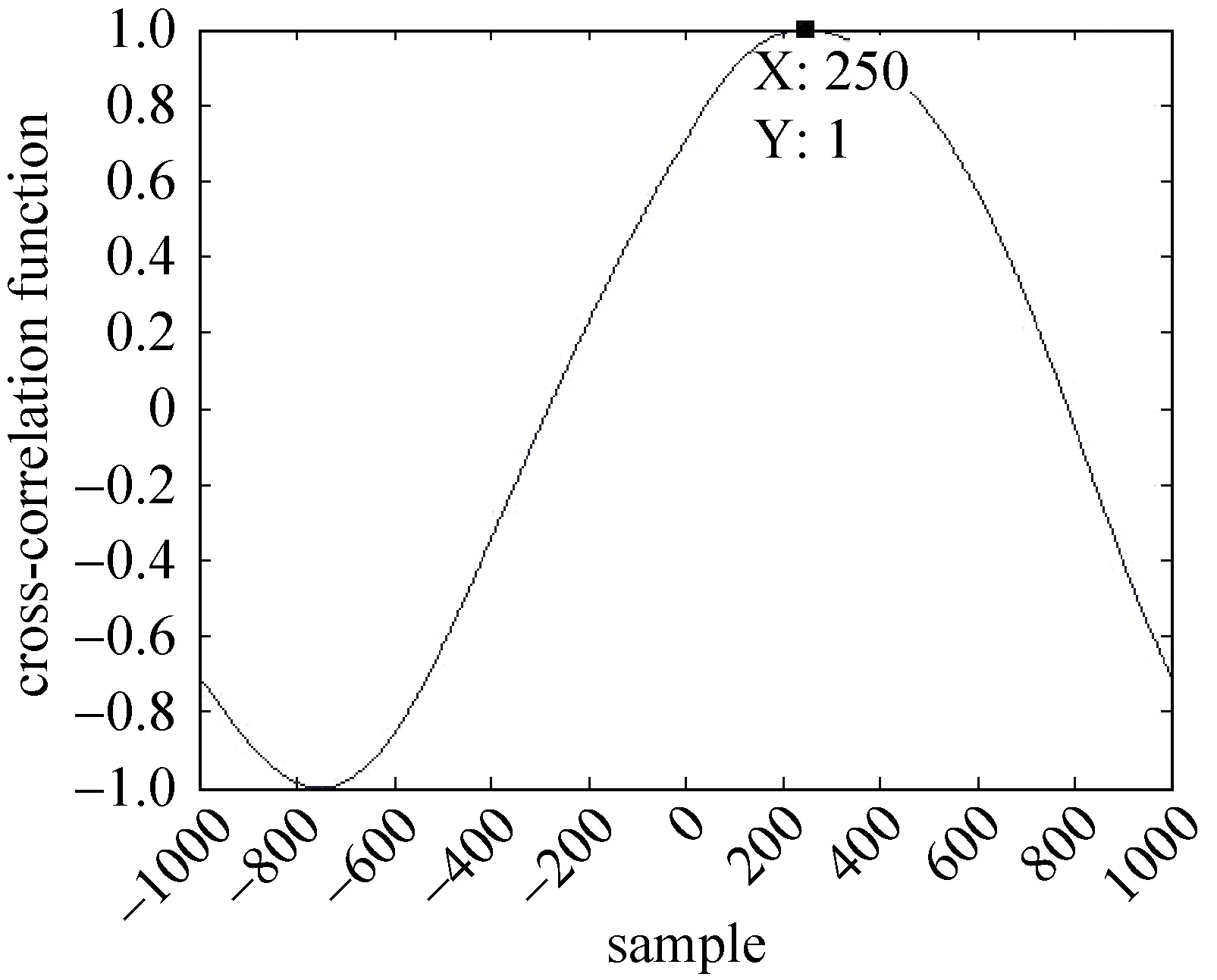
图1 广义互相关函数曲线Fig.1 The generalized cross-correlation function curve

3 应用分析

仿真验证的数据由于没有随机误差、漂移误差的干扰，可以得到比较精确的估计结果。为进一步验证算法在实测数据计算过程中的适应性，下面以某导弹试验数据为源信号，以雷达弹道数据为参考值，提取遥测数据时延值，对弹道进行修正，并对修正效果进行了详细分析。

3.1 遥测信号预处理

GNSS数据采样率为1Hz，由于其采样速率较低，难以精确计算时延，首先对数据进行预处理。图2（a）所示为未处理的遥测GNSS弹道高程数据，图2（b）所示为经过最小二乘拟合以及插值后的数据，对比可知数据拟合趋势较好，GNSS数据采样率由1Hz提高到了1000Hz。

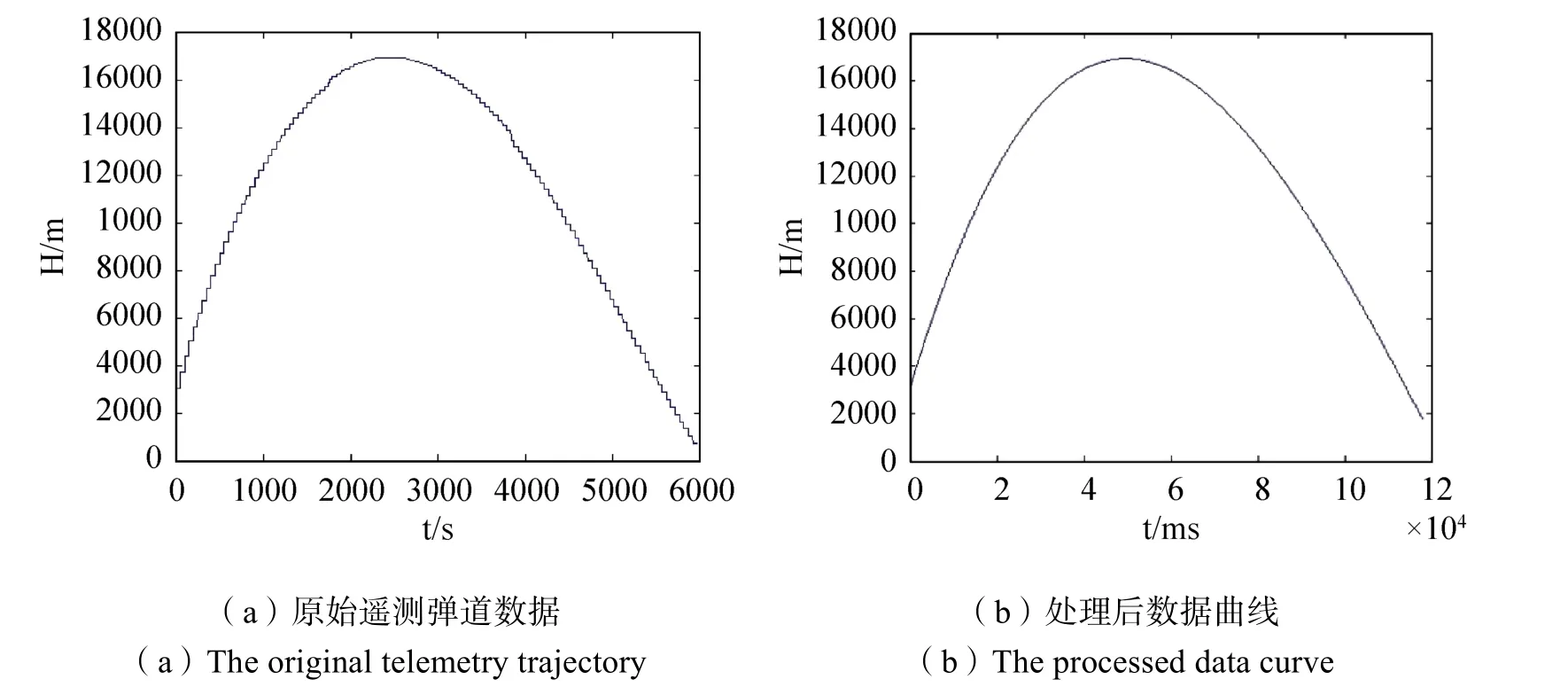
图2 遥测数据处理前后对比图Fig.2 Comparison of original data and processed data of telemetry trajectory

3.2 时延提取和修正

在数据预处理的基础上对遥测弹道提取时延。时延体现在弹道上的就是位移的滞后，遥测GNSS弹道数据和雷达测量弹道数据如图3所示，遥测数据明显较雷达数据有所滞后，尤其在上升段和下降段。这是由于上升和下降阶段弹丸速度较大，而时延在整个弹道过程中趋于一定，导致时间一定时速度较大的阶段位移延迟也相应较大。解算的弹丸GNSS垂直速度分量曲线如图4所示。

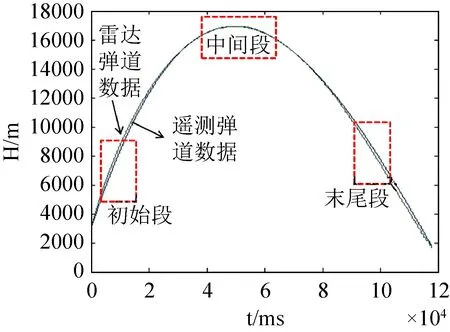
图3 遥测与雷达数据对比图Fig.3 Comparison of telemetry trajectory and radar trajectory

图4 弹丸GNSS垂直速度分量Fig.4 The vertical velocity component solved from GNSS trajectory data

利用广义互相关原理提取遥测弹道数据的时延，得到的互相关函数趋势曲线如图5所示，最高点出现在横轴为104的位置，乘以采样率即为延迟时间，由于数据采样时间间隔为1ms，因此计算所得时延为104ms。

最后利用提取的时延值对遥测弹道进行修正，修正公式如下：

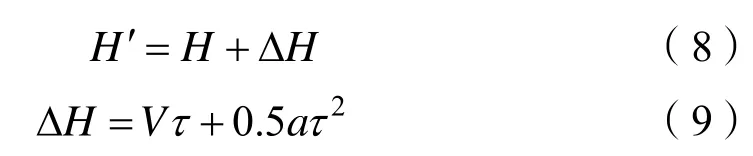
其中，H为未处理的遥测弹道数据，ΔH为利用时延修正的高程差，′

H为修正后的弹道数据，τ为提取的遥测弹道数据时延值，V为修正时刻速度，a为修正时刻加速度。

图6（a）所示为雷达弹道和修正后遥测弹道对比图，图6（b）为弹丸发射第8至10秒的局部放大图，可见弹道修正效果明显，遥测数据和雷达数据基本一致，实现了利用时延修正遥测弹道的目的。

图5 遥测、雷达弹道数据互相关函数Fig.5 The cross-correlation function of telemetry and radar trajectory data

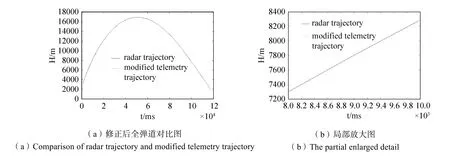
图6 修正后遥测弹道和雷达弹道对比图Fig.6 Comparison of modified telemetry trajectory and radar trajectory

为了更加直观地观察修正效果，对雷达弹道和修正前、后遥测弹道的差值进行对比，如图7所示。可以看出，修正前差值最大处可达近80m，修正后差值不超过10m，修正效果较好。

图7 雷达弹道与修正前、后遥测弹道的差值对比Fig.7 Comparison of the difference between telemetry and radar trajectory before and after modification

4 结束语

针对遥测弹道测量时延问题，以雷达数据为参考值，通过广义互相关计算提取时延值，对遥测弹道进行修正，提高遥测设备弹道测量精度。本文在对遥测弹道数据预处理的基础上，建立广义互相关模型，计算互相关函数峰值提取时延，并通过仿真和试验数据验证了算法的正确性。