一种基于多项式函数的VSSNLMS算法*

周胜文，石 俊，周云生，詹 磊

（北京遥测技术研究所 北京 100076）

引 言

归一化最小均方误差NLMS（Normalized Least Mean Square）算法是自适应滤波应用中最小均方误差算法LMS族中最常用的一种算法。它的优点是在输入信号较大的情况下可避免梯度噪声放大的干扰，因此具有更好的收敛特性。但是与LMS算法一样，NLMS算法步长的选择对其性能的影响很大。小步长可使滤波器收敛得更稳定，但是收敛速度过慢；大步长可以加快收敛速度，但是稳态均方误差较大。

为了解决收敛速度与稳态误差之间的矛盾，各种变步长归一化LMS（VSSNLMS）算法应运而生。VSSNLMS算法基本上遵循如下步长调整原则：在初始收敛阶段或未知系统参数发生变化时，步长比较大，以便有较快的收敛速度或对时变系统的跟踪速度；而在算法收敛后，应保持较小的调整步长，以达到较小的稳态误差。

本文分析相关文献中的变步长NLMS 算法，在此基础上提出一种新的基于多项式函数的变步长NLMS算法，同时实现较快的收敛速度和较小的稳态误差，并且实时计算量较小，有利于工程应用。

1 VSSNLMS算法

最小均方（LMS）算法是一种以瞬时误差信号平方的梯度作为均方误差函数梯度估计的线性自适应滤波算法，其实现结构简单，是一种使用广泛的自适应算法。但它对于初始收敛速度、时变系统跟踪能力及稳态误差这三者的要求是相互矛盾的。

归一化LMS（NLMS）算法[1]通过对迭代步长因子进行归一化，来确保自适应滤波算法收敛的稳定性。但是和LMS算法一样，它的收敛速度和稳态误差也要受到步长的控制，步长大则收敛速度较快而稳态误差较大，步长小则收敛速度较慢而稳态误差较小，因此需要采用变步长算法实现收敛速度和稳态误差的平衡。

变步长LMS（VSSLMS）算法[2,3]能同时获得较快的初始收敛速度、时变系统跟踪能力以及较小的稳态误差。但是对于脉冲信号而言，在脉冲间歇期内无有用信号，而VSSLMS的步长因子μ(n)在脉冲间歇期内仍然继续减小，导致在下一个有用脉冲信号到来时刻，步长因子μ(n)变得太小，不能起到快速收敛的作用。

因此，诸多文献将VSSLMS算法和NLMS算法相结合，提出变步长归一化LMS算法，它兼具初始收敛速度快、时变跟踪能力强、稳态误差小、对输入信号适应性强等优点。各种VSSNLMS算法的不同在于变步长因子的选取不同，VSSNLMS的滤波器权矢量更新基本公式为

式中，W(n)为滤波器的权矢量，X(n)为输入信号矢量，e(n)为误差信号。文献[4,5]提出一种基于sigmoid函数的VSSNLMS算法（SF-VSSNLMS），其变步长因子为

式中参数α主要用来控制步长的变化范围，参数β主要用来控制步长变化函数的陡峭程度。该算法具有较快的收敛速度和时变跟踪能力，然而由于sigmoid函数的本身缺陷使步长因子在误差e(n)接近零处存在较大的变化，不具备缓慢变化的特点，导致在算法收敛后仍存在较大的稳态误差。

文献[6]基于指数函数的VSSLMS算法和文献[7]基于指数函数的VSSNLMS算法（EF-VSSNLMS），变步长因子都为

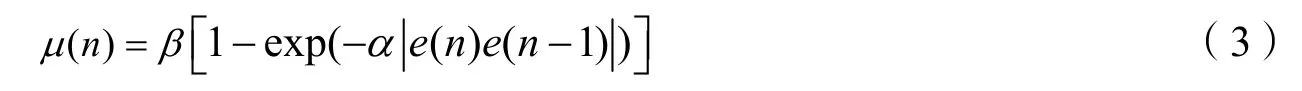
该算法在误差e(n)接近零处具有缓慢变化的特点，克服了SF-VSSNLMS算法在稳态收敛阶段步长变化较大的不足。同时，算法具有较好的收敛速度。其缺点是抗噪声能力不强，影响该算法在低信噪比环境下的精度。

文献[8–10]提出的算法可以归纳为基于钟形函数的VSSNLMS算法（BSF-VSSNLMS），其变步长因子为

式中μmax是钟形函数的上界，选择为可收敛步长的最大值，a与b决定了函数曲线的形状，影响收敛速度和稳态误差。b决定了小步长与大步长之间过渡带的坡度，b越大，过渡带步长变化越快，曲线越陡峭。a决定了小步长的误差范围，从而决定了系统稳态范围。

文献[11，12]提出的算法可以归纳为基于余弦函数的VSSNLMS算法（CF-VSSNLMS），其变步长因子为

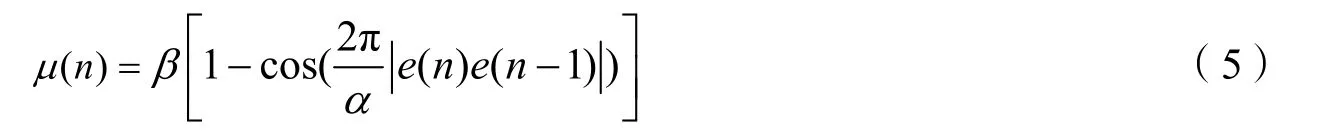
式中参数β控制步长曲线的取值范围，影响算法的收敛速度；α控制步长曲线在误差接近零时的形状。

文献[13]提出的基于双曲正割函数（hyperbolic secant function）的VSSNLMS算法（HSF-VSSNLMS），其变步长因子为

式中α、β、γ为控制步长因子的调节参数，α用于控制步长倾斜度，α值越大，步长函数收敛速度越快；β用于控制步长的变化范围，β越大，步长函数范围越大；γ用于控制步长函数的衰减速度，γ越大，步长函数的衰减越快。

2 基于多项式函数的VSSNLMS算法

从前节可以看出，各种变步长NLMS算法的变步长因子都是基于指数、余弦、双曲正割等复杂函数，在工程实现时变步长的实时更新需要进行查表计算。由于实际误差值e(n)在不同的输入信号带宽时存在较大范围波动，为了实现对不同e(n)值变步长因子的计算，查询表的规模会非常大。本文提出一种基于多项式函数的VSSNLMS算法（PF-VSSNLMS），其变步长因子是实时误差值e(n)的多项式组合，非常方便实时计算。PF-VSSNLMS的变步长因子为

式中参数α和β决定了变步长函数曲线的形状，影响收敛速度和稳态误差。β决定了小步长和大步长之间过渡带的坡度，β越大，过渡带坡度越大，曲线越陡峭；α决定了步长的取值范围，α越大，步长取值范围越小。

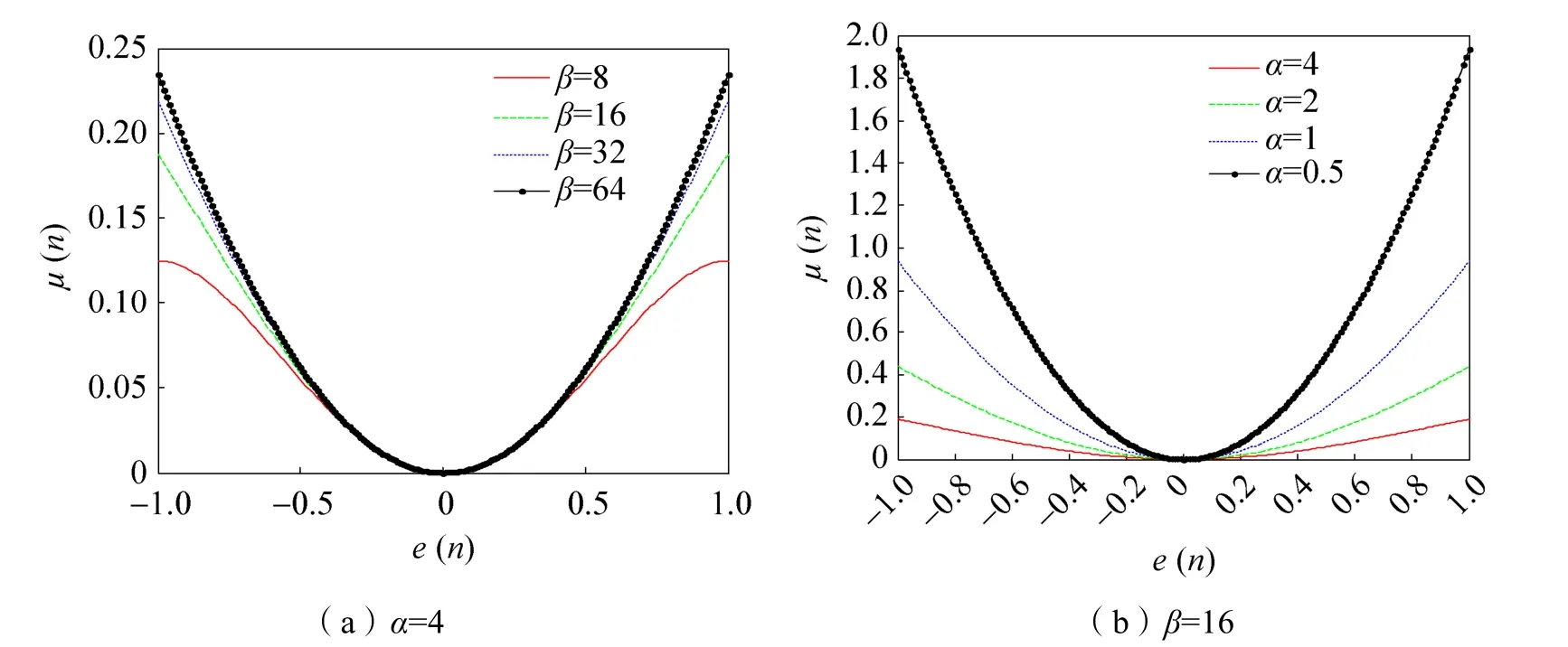
图1 α和β取值对变步长因子的影响Fig.1 Influences of α and β on variable step size factor

参数α和β取不同值时变步长因子如图1所示。从图1可以看出，参数α和β的取值范围应该适中，取值太小会导致收敛速度过慢，取值太大会导致稳态误差过大，本文中选取α=4、β=16进行算法仿真以及性能分析对比。

3 算法分析与仿真

在不同输入信号带宽和不同信噪比条件下，利用Matlab软件对PF-VSSNLMS算法进行蒙特卡洛仿真，并与基于指数函数、sigmoid函数、双曲正割函数、余弦函数、钟形函数的VSSNLMS算法进行性能对比。仿真时采样频率fs=1000MHz，采样点数N=2048，滤波器阶数K=128，蒙特卡洛仿真次数为100次。

3.1 不同信噪比条件下性能仿真

PF-VSSNLMS算法及其他五种同类算法在信噪比SNR为3dB、0dB、–3dB时自适应滤波收敛曲线如图2所示。从图2（a2）、（b2）、（c2）三张局部放大图可以看出，PF-VSSNLMS算法在不同信噪比条件下，收敛速度较快，稳态误差较小，性能优于其他同类算法。

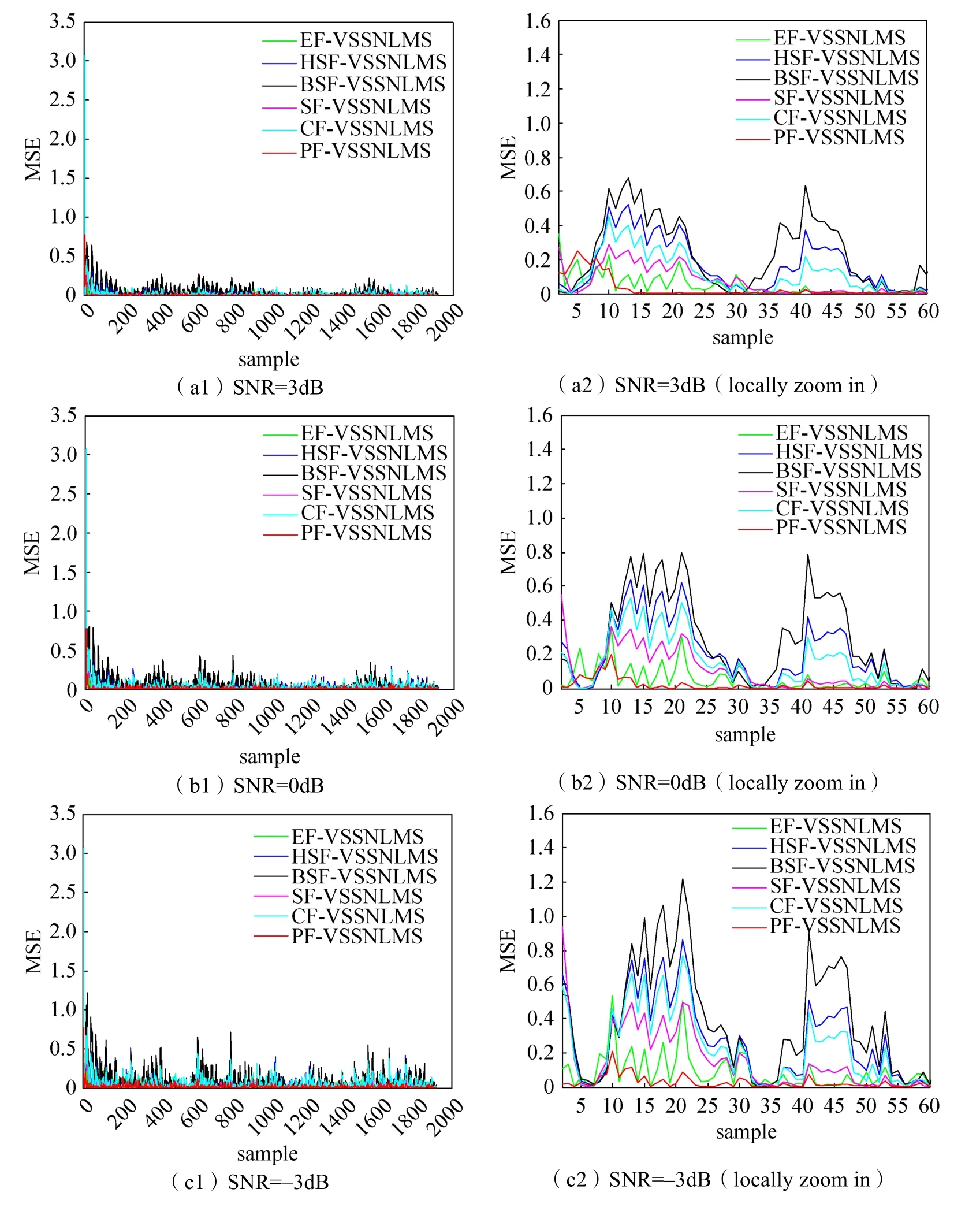
图2 PF-VSSNLMS算法和同类算法在不同信噪比条件下收敛曲线对比Fig.2 Comparison of convergence curves of PF-VSSNLMS and other VSSNLMS algorithms in different SNR

3.2 不同输入信号带宽条件下性能仿真

仿真时信噪比SNR=0dB，信号频率f0=20MHz，分别在信号带宽为0MHz和20MHz条件下对PF-VSSNLMS算法和其他同类算法进行100次蒙特卡洛仿真。不同输入信号条件下算法收敛曲线如图3所示。从图3可以看出，随着输入信号的改变，PF-VSSNLMS算法在不调整参数的情况下，相比其他同类算法，收敛速度更快，稳态误差更小。

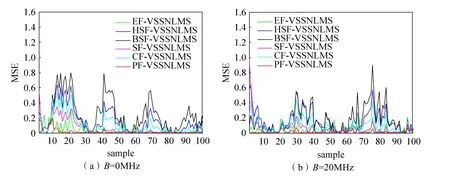
图3 PF-VSSNLMS算法和同类算法在不同输入信号带宽条件下收敛曲线对比Fig.3 Comparison of convergence curves of PF-VSSNLMS and other VSSNLMS algorithms in different input signal bandwidths

4 结束语

本文结合现有变步长归一化LMS算法的优点，从工程实际应用角度出发，采用多项式函数进行变步长因子调节，提出PF-VSSNLMS算法。该算法步长调节参数少，实时运算量小，在低信噪比条件下具有较快的收敛速度和较小的稳态误差，而且在不同输入信号带宽条件下，算法的收敛曲线比较稳定，相比其他同类算法整体性能更好。PF-VSSNLMS算法计算量不大，易于硬件实现，具有一定的工程应用价值，后续将继续开展硬件平台的验证实现等工作。