需求和回收对集成混合库存系统成本影响研究

宁鹏飞，丁玉珍，滕彦彬 （广州工商学院，广东 广州 510850）

0 引言

近年来我国经济的快速发展，促进人们环保意识的增强及相关环保法规的完善，生产企业要对其生产的产品全程负责，包括其废旧产品的最终处理。2015年《中华人民共和国环境保护法》中重点强调了要促进清洁生产和资源循环利用，按照规定对生活废弃物进行分类放置，减少日常生活对环境造成的损害。传统上废旧产品的处理采用循环回收处理模式，先拆解、分类，再通过物理化学处理方法，提取其中可再加工使用的原材料。而对其它由于经济技术原因无法回收的废旧产品等，则经过一定措施后采用直接废弃处置（disposal）模式。当前，废旧产品再制造（remanufacturing） 技术引起了人们的广泛关注，此模式在不影响经济发展前提下对环境影响更小，更加符合经济和环保协同可持续发展理念。再制造（remanufacturing）是通过必要的拆卸、检修和零部件更换等，将废旧产品恢复得如同新的一样的过程，适用于汽车、计算机、打印机、复印机、手机、电视机、冰箱、空调、洗衣机、轮胎、印刷电路板等众多产品[1]。废旧产品再制造一般需要原始产品生产的有关信息和较高的处理技术，通常由原始设备制造商（OEM）来完成，由此形成了制造/再制造混合系统（如图1所示）[2-5]。

库存的主要作用是协调供需关系的不平衡。针对库存数量的增减，需要制定合理的库存控制方法。如果库存控制不当，过多过少都会增加库存成本。库存太多会影响公司资金周转并带来积压物料的有形和无形损失；库存太小就可能缺货影响生产的连续性。库存大小又难以确定，随供需情况、新产品、季节等都会对其有较大变化。Erwin等人提出了Push和Pull随机混合库存控制策略尽管给出了双库存控制模式，但这些模式存在极大库存点无法解决。本文在集成Push-Pull库存控制策略基础上考虑了回收件存在废弃处置的情况下，研究废旧产品需求和回收相关条件下的关系，及其对制造/再制造混合库存成本的影响规律，从而为废旧产品回收双库存系统决策方式提供技术支持。

图1 混合库存系统

1 需求与回收相关的制造/再制造混合库存模型

本文构造了具有提前期条件下集成制造/再制造混合库存系统（如图2所示）。本模型主要增加了参数sd，来限制极大库存点造成的库存资源的浪费[6]。其库存控制策略为：

（1）回收件日常存储在回收件库存中。每当回收件库存达到库存最大值Qr时，要先检测可用件库存。如果可用件库存小于参数sd，要对回收产品进行再制造生产，经提前期Lr后到达可用件库存；否则回收产品经无害处理后直接废弃。

（2）每当可用件库存小于sr后检查回收件库存，当回收件库存和可用件库存总量达到Sr时立刻对回收件再制造，经Lr后到达可用件库存。否则当可用件库存消耗低于安全库存sm后，进行新产品订货，补货到可用件库存量Qm后，并经Lm到达可用件库存。

图2 集成制造/再制造混合库存控制策略

1.1 模型假设

本文采用了混合库存仿真方法。不失一般性，可以把连续的时间分成多个时间段，在任一时间段t的需求量为Dt，它将在使用时间Rj后回收。其回收持续时间为Rc，如在此期间不能回收的产品，进行废弃处理。其中Dt、Rj、Rc都不是固定值，根据调查数据分析，这些参数主要按照泊松分布进行处理。根据描述第x时间段销售的产品在第y时间段的回收量为Rxy，其它参数含义见本文1.2小节。

由于混合库存系统很多参数的不确定性，为了便于求解，本文库存系统要满足以下条件：

（1） 需求和回收参数服从泊松分布，其参数分别为λD和λR，且λR＜λD；

（2）本文只考虑单个产品的混合库存情况。

1.2 符号定义

（1） 成本因素

（2）其它参数定义如下：

t：时间段 0,1,2,3,…,T；

Is（t）：t时间段开始时的库存位置；

Im（t）：指在时间段t-Lm初时的新产品订货量，即在t时间段初时到达可用件库存的新产品订货量；

Ir（t）：指在时间段t-Lr初时的再制造产品订货量，即在t时间段初时到达可用件库存的再制造产品订货量；

Bt：t时间段初的缺货量；

dt：t时间段初的废弃处理量；

Dt：t时间段内需求量（各时间段内相互独立，服从泊松分布）；

Rt：t时间段内回收量（各时间段内相互独立，服从泊松分布）；

Dmt：t时间段初决策的新产品制造量；

Drt：t时间段初决策的再制造产品制造量；

Ymt：在t时间段内如果有新产品订货为1，否则为0；

Yrt：在t时间段内如果有再制造产品订货为1，否则为0；

1.3 建立模型

文献[6]库存模型中的需求和回收各自独立产生，即每个时间段回收的产品量没有关联。但在现实生活中每个时间段产生的回收产品量是由过往多个时间段的累积需求产生的。本文库存模型主要研究需求和回收相关情况下，对混合库存成本的影响规律。但由于企业回收能力所限，有些到期要回收的产品不得不废弃或者由购买者自行处理。图3是需求和回收相关的产品回收时间简图。产品在t1和t2时间段内的需求量分别为Dt1和Dt2。经过时间间隔Rj产品开始回收，并随机按照泊松分布进行，其概率密度为φt1和φt2。要在产品的回收持续时间Rc内完成，部分产品在这期间将没有回收废弃处理。任何时刻（如图t2+Rj时间段）的回收量由之前多个时间段在此时进行回收量的累积之和构成。

根据以上描述可知在t时间段的需求量Dt可表示为：

图3 需求的回收相关的产品回收时间简图

即x时间段出售的产品在过后连续时间段回收量之和。不失一般性，为了简明其y可以从0开始取值（y为0时表示x时间段消费的产品首次回收，以此类推）。因此，Dt可表示为：

t时间段的回收量Rt可表示为：

即y时间段回收的产品为之前的连续时间段在此时间段回收量之和。同样，其x也可以从0开始取值（x为0时表示最早出售的产品在此时间段回收的时间，以此类推）。因此，Rt可表示为：

回收率λ的计算方式为：

根据上面分析t时刻的总成本为：

模型求解目标是单位时间段内的平均成本C，则其目标函数为：

式（7）在T时间段内同时需满足以下条件：

1.4 算法设计

以上模型的需求和回收变量是随机的，针对其计算的复杂性本文使用仿真方法进行计算。其计算过程如下：（1）初始化，对赋予初始值，计算C（0）。（2） 计算机按照泊松分布随机获取此时间段的需求量。（3）按照某一分布取得这一时间段回收时的泊松分布参数值。（4）计算之前每个时间段在此时的回收量，从而根据式（6）得到这一时间段的总回收量。（5）在时间段t初进行决策，在t时间段初的总成本为：如果t+1≤T（T值取尽可能大的值），则转入步骤（2），进行下一时间段的计算。否则转入步骤（5）。（7） 根据式（2） 计算平均库存成本（8） 变化提前期Lm,Lr的值，确定其值是否遍历完毕。否则转入步骤（1），分析平均库存成本随提前期变化的规律，得出近似最低平均成本。

2 算例仿真

以某可再制造商品的需求和回收为例，在本例中假定时间段t的单位为天，成本单位为元。相关取值见表1、表2，T值取50 000。

表1 库存限制参数

表2 成本因素

此商品每天的平均需求量为300个，当天的需求在此后400天时开始回收，持续回收不超过300天。每天的回收比例按照某一概率分布进行计算，此分布参数φt在开始回收时随机产生，直到回收周期完成为止。本次程序使用VC++6.0，下面是此程序的运行结果。由于数据比较多，本次给出lm为3时各参数随lr的变化情况及lr为4时各参数随lm的变化情况。

从表3和表4可知，需求和回收对平均成本的影响都符合先递减后递增的规律。由于需求和回收相关更加符合实际情况，此例能更好地说明提前期对平均成本的影响程度和原因。从表中可以看出，提前期的变化对废弃处理量的影响比较小，主要还是对可用件库存成本和缺货成本的影响比较大。因此，可用件库存成本和缺货成本是考虑成本因素中的主要因素，二者符合效益背反原理。只有在生产中给予重视，才能达到成本的最小化，效益的最优化。

表3 需求和回收相关的平均成本变化表（lm= 3）

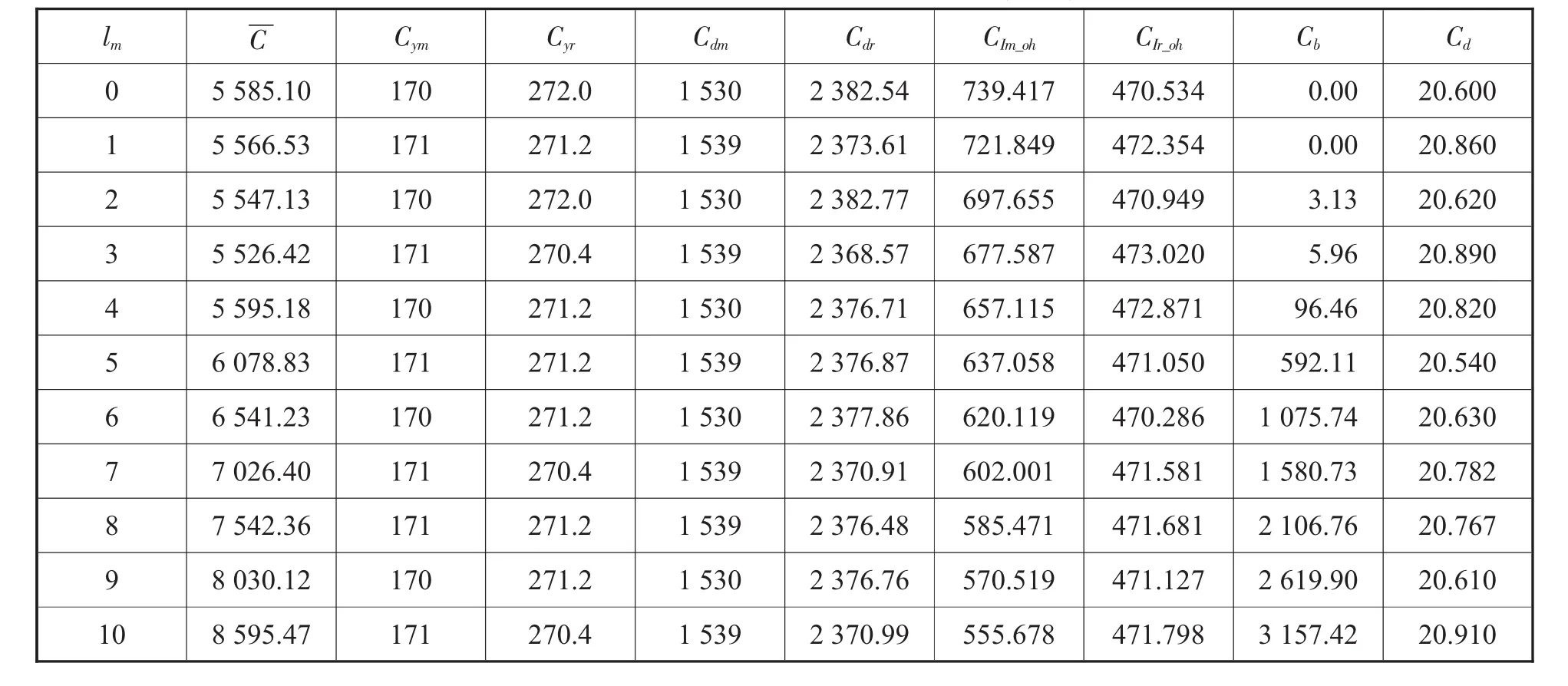
表4 需求和回收相关的平均成本变化表（lr= 4）

此案例说明在实践中可模拟制造/再制造集成库存实际情况，归纳各参数对平均总成本的变化规律，从而得出最佳库存控制策略，为企业库存决策提供依据。

3 结论与展望

本文主要构建了制造/再制造集成库存策略，与传统PUSH和PULL策略相比，主要优点是在库存条件相同时增加再制造产品的订货频率，减少废弃处理量和缺货水平，从而创造公司利益最大化。从仿真案例的各表中可以看出，平均总成本随提前期增加而增加，因此在现实中要尽量缩短提前期。受提前期变化影响最大的是平均缺货成本，平均缺货成本随提前期延长而快速增长，但在一定影响因素下会随提前期延长先减少后快速增长（如表3）。尽管再制造产品固定订货成本、回收件库存成本有所提高，但从整体上来看，集成策略的平均成本在同等条件下也较小。通过比较可知，集成库存策略比PUSH和PULL策略在现实中有很好的适用性。本库存策略的建立更真实地反应了混合库存在随机需求和回收条件下的变化规律，可以为回收企业在库存管理时提供参考数据，如何有效降低混合库存管理成本。另外鉴于传统算法的复杂性，本文使用了模拟方法进行求解。通过和传统方法比较，其结果几乎一致，但此法更加简单适用。

本文构建的制造/再制造集成库存策略对于企业再制造产品回收虽然有很多方面的有力支持，但企业决策还是要以自身盈利才是长久之计，符合社会可持续发展之路。作者后续将继续更深入地研究再制造产品政策和法规，进而推动再制造产品的健康快速发展，为社会可持续发展贡献自己一份力量。