基于SAP2000的错层结构动力弹塑性时程分析

邹仁华，张 浩，张 琼，许嘉伟，杨 帆

（西安科技大学 建筑与土木工程学院，陕西西安 710054）

0 引言

为了解决错层框架结构中常出现短柱以及错层节点处传力路线差等现象，本文提出了带钢管混凝土柱的新型错层结构。目前国内外对此类新型错层结构抗震性能方面的研究少之又少，为此，本文利用SAP2000弹塑性时程分析，对此类工程的抗震性能进行系统的研究。

1 错层结构计算模型

1.1 CG1结构模型概述

本文所选择的工程计算模型为错层框架结构，在2、4轴线处错层，布置位置对称。建立钢筋混凝土错层结构将其标记为GC，建立的带钢管混凝土柱的错层结构标记为XGC。建筑结构总高度为16.5m，总长度为24m，总宽度为10.8m。首层高度为4.5m，其他层为3m。错层部位首层为3.6m，错层高度。

混凝土为C35，钢管选择Q235，该建筑的抗震设防烈度为8度（0.2g），设计地震分组为第二组，场地类别为Ⅱ类。该工程选择柱下独立基础，并采用不上人屋面。错层框架结构中的节点无特殊处理，其结构的平立面布置图如图1所示。

1.2 其他工程模型的建立

钢管混凝土构件的受力情况有别于一般混凝土构件，其主要影响因素是钢管对混凝土的约束作用。参照韩林海对钢管混凝土柱的研究[1]，以及对方形钢管混凝土柱抗剪性能方面的研究，本文设计了五个工程建模方案，如表1所示。

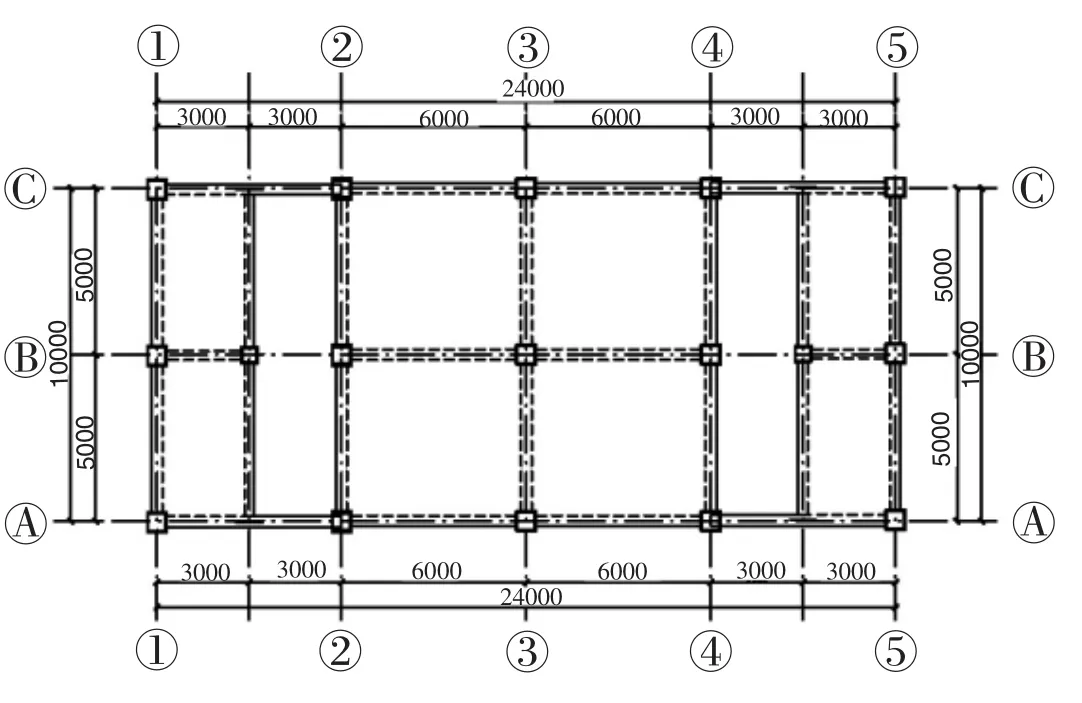
图1 GC1结构平面图

表1 设计主要参数及等级

2 工程有限元模型的建立

2.1 结构模型假定

（1）材料属性的定义

在建模过程中，对材料进行各向同性的假设，其表现为材料的行为独立于荷载方向或材料朝向，剪力行为与膨胀行为不耦合，并且不受温度的影响。一般混凝土和钢材都符合该假定。各向同性材料应变与应力以及温度变化的力学、热性能的关系如下式所示：

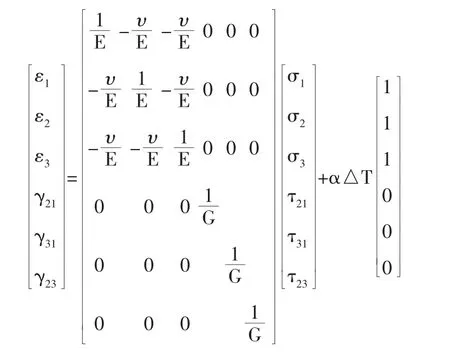
式中：E为杨氏弹性模量；υ为泊松比；G为剪切模量；α为热膨胀系数。

（2） SAP2000模型简化假定

依赖于《混规》5.1.5条对刚度楼板的相关规定，本文建模中楼板采用刚性隔板假定，有限元建模中用薄壳单元（SHELL）来模拟分析。该假定减少了结构的计算自由度，从而缩减后期系统中求解方程的数量，使程序计算效率大大提升。

将梁柱构件简化为空间杆，并都用杆单元进行建模，只考虑单元的剪切变形和轴向变形。并将处于错层的梁柱连接节点假定为理想铰接。

2.2 结构模型的建立

（1）单元的剖分

工程模型在进行有限元分析之前，需要对其相关构件进行单元网格划分，其最低要求是保障每个研究对象的计算精度。本文SAP2000工程中壳单元采用自动网格划分，并将最大剖分长度设置为1.2m。

（2）质量源的定义

SAP2000程序提供给我们质量源的定义方式有三种，本文选择“来自荷载”这一方法，并遵循《荷载规范》选择荷载组合方式，即恒荷载加1/2的活荷载的组合方式。

（3）错层模型的处理

错层结构会出现在同一层中两个不同标高的楼板，本文在SAP2000建模时采用的方法是按照两个标准层来建模，其相当于楼板大开洞的情况，从而实现错层楼板的布置。

（4）钢管混凝土柱截面的定义

本文对钢管混凝土柱建模，定义材料分别为钢管选用Q235，截面设计选择“箱型截面”；混凝土选用C35并设定为约束模式，截面设计中采用矩形截面。利用Xtract进行钢管混凝土柱截面设计计算，并得出相关铰属性的定义参数。

应用软件SAP2000进行结构模型建立，其由各种梁柱杆系单元以及薄壳单元组成有限元空间分析模型，如图2所示。

2.3 铰属性特征值有效性的验证

通过SAP2000对文献[1]的试验模型进行建模并对其进行Pushover分析，并将输出的模型顶点的荷载位移曲线与试验结果对比，从而验证本文提及的铰属性特征值的确定方法是否有效，具体结果如下图3和图4所示。

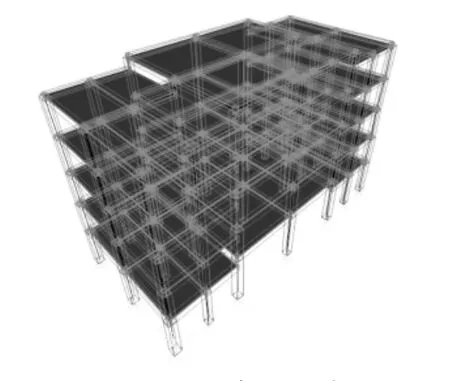
图2 GC1有限元空间分析模型

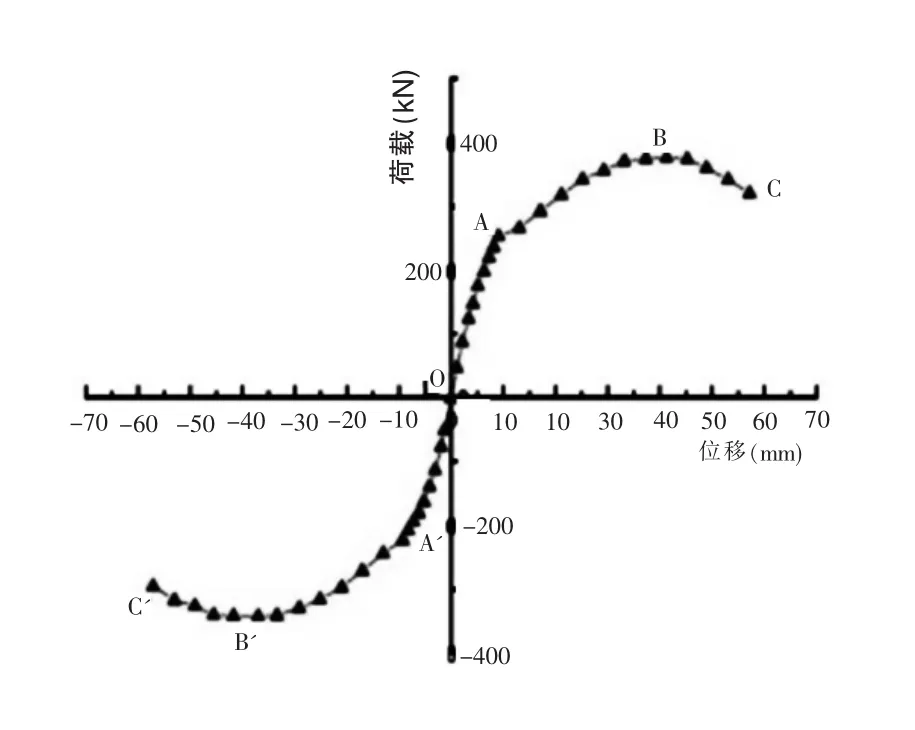
图3 顶点位移试验结果图示

图4 顶点位移Push-over分析结果图示

在加载工程中整体结构经历了弹性、弹塑性工作阶段和破坏阶段。试验结构破坏时塑性铰的出现顺序是先在底层梁端出现塑性铰，然后是二层梁端，最终底层柱底出现塑性铰而导致框架破坏，塑性铰的发展过程符合“强柱弱梁”的设计理念。在加载的过程中，控制位移所施加的侧向力为F=46.86~191.17kN时，荷载-位移曲线可近似为线性段，结构处于弹性阶段；当侧向荷载F=219.61kN时，结构出现屈服，靠近施载底层梁端出现塑性铰；侧向位移△=41.28mm时，结构承受最大侧向力F=375.57kN，此时柱底出现塑性铰，结构的承载力开始下降。整体而言，试验得到的荷载-位移曲线较光滑[2]。

通过SAP2000建立试验模型，并利用Push-over计算的基地剪力-位移曲线如图4所示。从图中可以看出，模型计算试验模型的极限承载力为F=366kN，计算的顶点位移为△=36.4mm，可得出两者的误差分别为2.5%和11.8%。在模型分析中塑性铰的出现顺序和试验结果显示中相一致，并在顶点位移为△=36.4mm时，模型中的塑性铰全部出现，标志着构建端部各个截面逐渐开始退出工作，结构整体的承载力出现显著下降的趋势。

根据基底剪力-位移相关数据的对比和塑性铰的发展情况进行分析对比，依据分析结果可以得出建立的此类分析模型中塑性铰自定义的方法是切实可行的，能够有效确定钢管混凝土柱塑性铰的特征值相关参数。

3 动力时程分析

3.1 时程分析理论

《建筑抗震设计规范》（GB 50011-2010）第 3.6.2条规定“不规则且具有明显薄弱部位可能导致地震时严重破坏的建筑结构，应按本规范有关规定进行罕遇地震作用下的弹塑性形分析[3]。此时，可根据结构特点采用静力弹塑性或弹塑性时程分析方法。对于高阶振型且比较复杂的结构，由于在第一阶振型结构运动中结构本身的薄弱部位不一定会显现出来，或者当结构虽然产生了较大的扭转效应，但是并没有在静力非线性分析中得到反应，这类结构就需要应用动力弹塑性分析方法来分析罕遇地震作用的位移反应[4]。

本文选择两条实际地震波以及一条人工波，分别为Lan Zhou 1波、EL-Centro波和Tang Shan EW波，对上面提及的5个工程模型进行时程分析。其通常采用的积分方法主要有Newmark法、Wilson法和HHT（Hiber-Huges-Taytor）法，本文选择HHT法进行数值计算。HHT法其实是对Newmark法的改进与提升，用系数对结构的运动方程进行调整，由Huges在1987年的时候提出。

3.2 时程分析结果

在三条时程波作用下，对各工程模型进行非线性时程分析，本文从结构变形、楼层剪力和塑性铰的发展这三方面进行对比分析，探讨了设计方案中提及的两个变量参数对工程模型的影响状况，对XGC模型抗震性能的影响因素进行评估。

选择LanZhou1波时程分析输出在X方向的数据进行分析，下面分别给出了各个模型在Lan Zhou1波下的层间位移变化曲线和层间基底剪力图，如图5和图6所示。

图5、图6分别给出了LanZhou1波作用下，各个模型的层间位移和楼层剪力的数值变化曲线。通过对比，可得出下面相关理论：

（1）GC模型在X向的层间位移曲线既不符合典型剪切型的层间位移随层高增大而减小的趋势，也不符合弯曲型的随层高增加而增加的趋势。

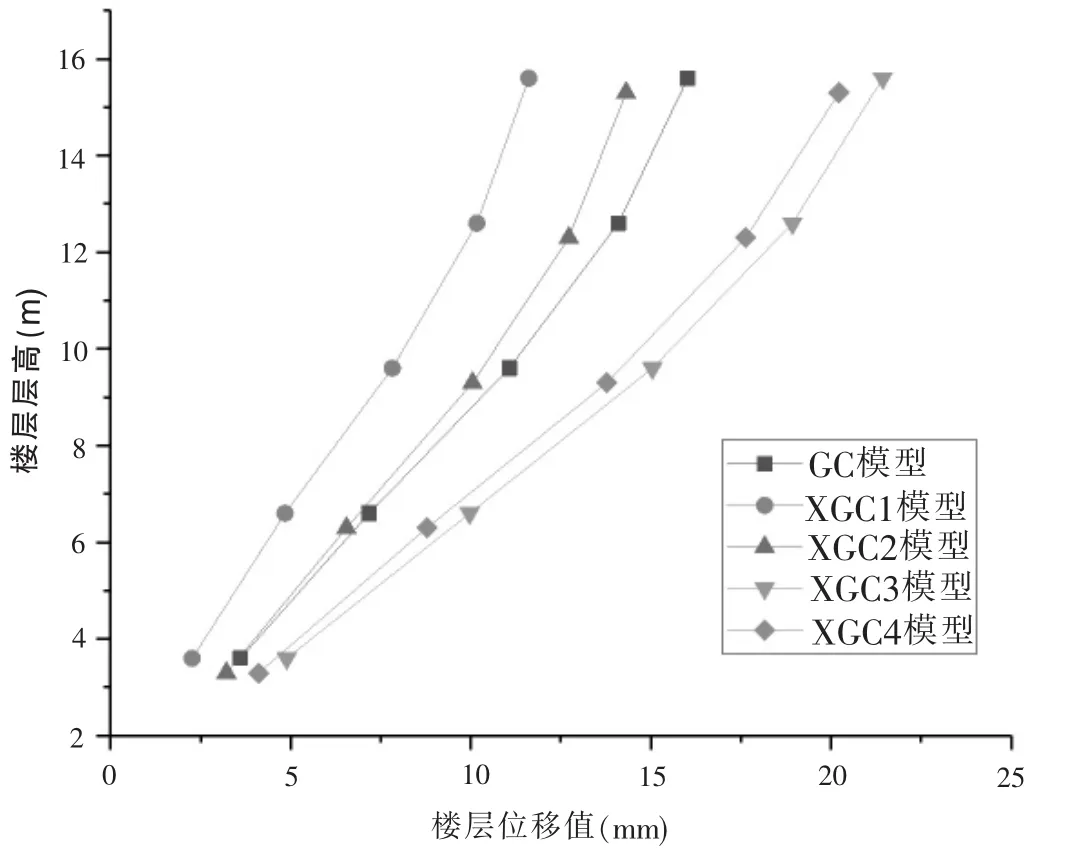
图5 各模型层间位移LanZhou1波图示

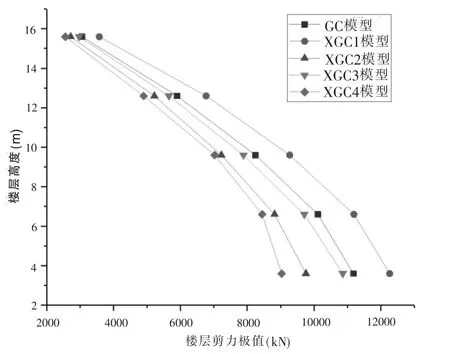
图6 楼层剪力极值LanZhou1波图示

（2） 图5中，通过对模型XGC1、模型XGC2和模型XGC3、模型XGC4对比，可得出XGC模型的钢管混凝土柱截面尺寸的增大，使得结构模型的楼层位移值也随之增大。通过这一现象，可以看出其自身质量大于刚度增值对位移值的影响。

（3）通过图7给出的各工程模型在LanZhou1波作用下楼层剪力极值的变化曲线，将各工程模型的剪力变化趋势两两对比，能够得出影响XGC模型楼层剪力值变化的主要因素是结构的错层高度。

通过时程分析输出数值的对比，得到EL-Centro波下输出的位移值最大。特此，在上面的基础上，提供罕遇地震下弹塑性时程分析的各个模型层间位移角的相关数值，利用抗震规范的相关规定进行验证分析。下面对该波下的层间位移进行整理计算，结果如表2所示。

表2 各工程模型弹塑性层间位移角结果示表

（4）抗震规范中对弹塑性层间位移角的规定限值为1/50，可看出各个模型都符合该项要求。表2中XGC1模型的层间位移角为1/61，远大于其他四个模型，并且其发生位置在12.6m处，其他的在9.6m处，可得出XGC1模型的整体刚度要小于其他模型。通过分析可发现，该现象的出现是因为相比于钢筋混凝土构件，其侧向刚度和错层节点处传力路径较差，而XGC1模型的错层高度较小无法完全发挥出钢管混凝土柱的延性，这正是仅相比于XGC2模型也会出现层间位移突变的原因。

3.3 塑性铰的发展

上面给出的位移、楼层剪力和层间位移角都是结构时程分析最终时刻的结果，无法反映工程真实受力的变形过程。为此，对各个工程在8度罕遇地震波作用下的塑性铰相关结果进行整理输出。下面以LanZhou1波为例进行相关结果输出，如图7所示。

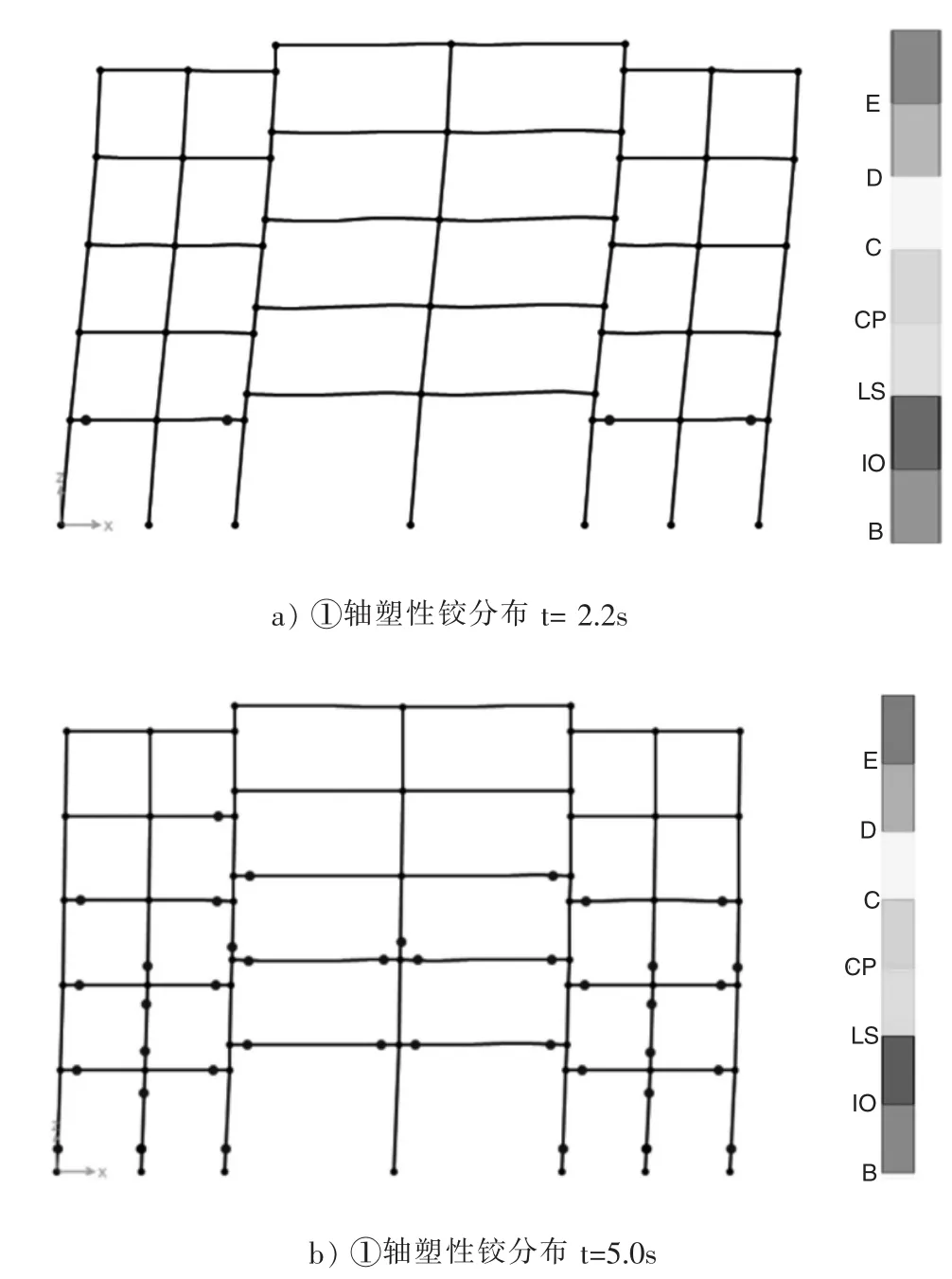
图7 GC模型LanZhou1波作用下塑性铰发展

图7 给出了在LanZhou1波作用下，GC模型塑性铰的出现情况，在2.2s时开始出现塑性铰，先是在第二层两端出现塑性铰，主要集中在错层柱两侧的梁端处；在5.0s时，即LanZhou1波幅值的极值出现时刻，逐渐在三、四层梁端处以及部分柱底端陆续出现塑性铰，出现塑性铰的混凝土柱主要分布于模型结构层高较低的两侧还有第三层；在7.6s时，首层柱底端首先进入破坏状态。通过上面可以看出，建立的GC模型虽然符合“强柱弱梁”的设计理念，但是因为错层的原因使得模型在第三层和错层节点处出现薄弱层，让模型的整体性变得较差。本文对其他四个带钢管混凝土柱的错层结构在LanZhou1波作用下其塑性铰的发展情况进行简单阐述，如图8—图11所示。

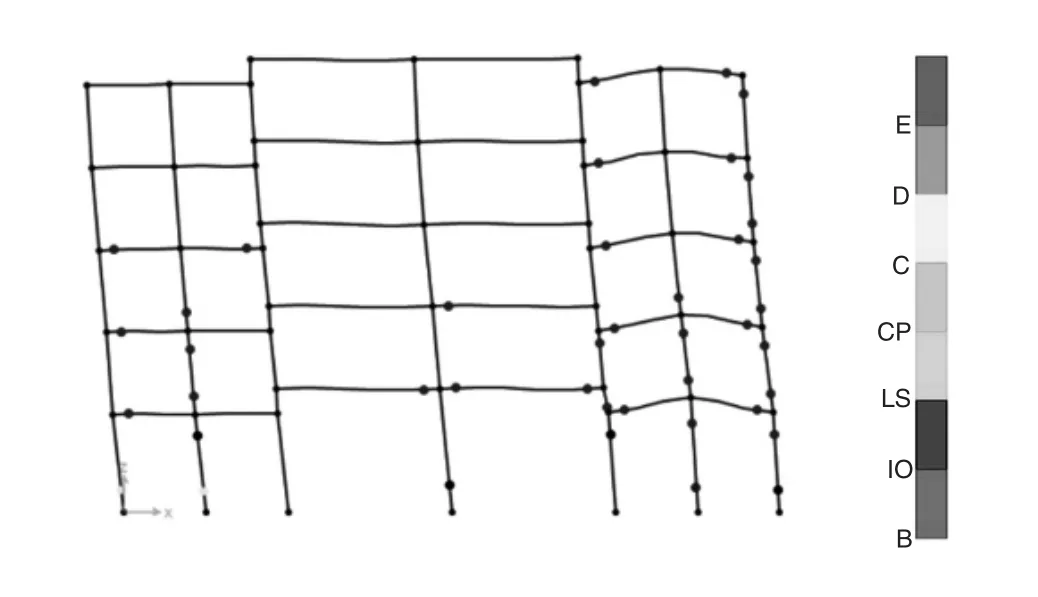
图8 XGC1模型塑性铰发展（t=6.0s）

图9 XGC2模型塑性铰发展（t=4.7s）

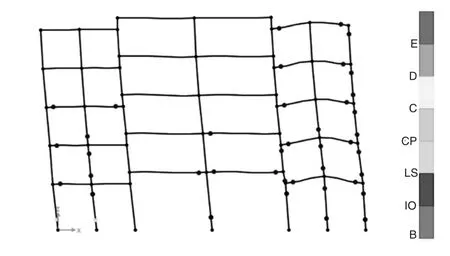
图10 XGC3模型塑性铰发展（t=6.0s）

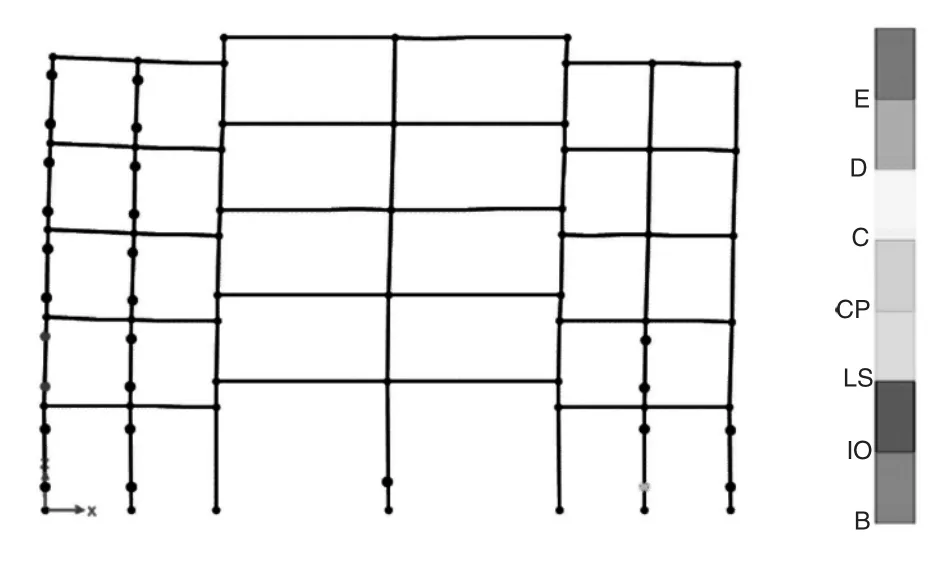
图11 XGC4模型塑性铰发展（t=9.2s）

图8 —图11展示出了四个带钢管混凝土柱的新型错层框架结构的塑性铰发展情况，可以得出模型XGC1和XGC2的塑性铰首先出现在轴线2、4的底层柱的底端，而其塑性铰极限破坏阶段分别在6.0s和4.7s，并且此过程中钢管混凝土柱上未出现塑性铰，其主要出现在两侧的梁柱构件上。可以得出虽然300*300的钢管混凝土柱能够提供与GC模型相当的承载力，且其自身延性较好，但是其侧向刚度较差，从而使得两侧梁柱上塑性铰出现的较为密集，这两个工程模型无法提供良好的抗震性能。

图11和图12为模型XGC3和XGC4塑性铰的发展图示，相比钢管混凝土柱截面尺寸较小的模型XGC1和XGC2，其塑性铰都是出现在2.2s时，在梁端和底层柱上陆续出现，其极限破坏阶段出现时刻分别为6.0s和9.2s。可以看出钢管混凝土柱与混凝土柱的侧向刚度相近时，在一定程度上，模型中错层高度越大，模型表现出的延性越好。

模型XGC4与模型GC相比，两种工程模型的极限状态出现时间分别是9.2s和7.4s，虽然后期都在第一、三层柱端出现塑性铰，但是对比可以发现，模型XGC4仅是在2、4轴零星出现，并在错层柱段处未出现塑性铰。上面的种种现象表明，相比于模型GC，在地震作用下，模型XGC4表现出来了较好的整体变形能力，并且极大地改善了模型GC1的抗震性能。

对建立的五种工程模型进行动力弹塑性分析，通过对塑性铰发展情况对比分析，可以得出模型XGC1和模型XGC2中的钢管混凝土柱的侧向刚度较小，无法改善GC模型塑性铰的发展情况。模型XGC3和模型XGC4塑性铰的发展情况符合“强柱弱梁”的设计理念，并且改善了原模型在错层柱段塑性铰的变形情况，相比较而言，模型XGC4破坏阶段出现较晚，表现出了良好的抗震变形能力。

4 结语

对各个模型进行动力弹塑性时程分析，通过对比三种地震波作用下，各个模型所展示出的结构变形和楼层剪力变化曲线，可得出仅依赖框架柱等轴压承载力替换得出的XGC模型无法满足结构侧向刚度的要求。

通过塑性铰出现和发展的趋势，发现GC模型在错层柱段易出现塑性铰，总结得出错层结构传力路径差和柱段短柱等因素，正是造成该模型抗震性能差的原因。相比较其他四个新型带钢管柱的错层结构，通过有限元模拟得出模型XGC1和模型XGC2虽然避免了错层处柱段塑性铰的出现，但其工程结构的侧向刚度差，因此其结构整体性也较差。模型XGC3和模型XGC4中塑性铰发展缓慢，未在错层处出现塑性铰，且相比于模型XGC3，增大错层高度使得柱底塑性铰退出工作的时间出现了延长。模型XGC3和模型XGC4极好地改善了模型GC的抗震性能。

通过对上面结论进行整理分析，可得出模型XGC3和模型XGC4能够改善GC模型的抗震性能，主要表现在避免了错层柱段处塑性铰的出现、延长了结构出现破坏的时间，以及避免了第三层薄弱层的出现，即本文提出的XGC模型确实对错层结构的抗震性能有极大的改善，为之后相关的工程实际应用和后期研究打下了坚实的理论基础。