基于正交多载波的导引头抗多目标干扰技术研究

李昊星，张 迪，高德亮，吕瑞恒，顾村锋

(1. 上海机电工程研究所，上海 201109； 2. 空军装备部驻上海地区第一军事代表室，上海 201109)

0 引 言

多目标密集突击空袭战术是现代战争中进攻方常采用的方式，为了有效对目标进行拦截，必须能够分辨、检测每个目标,并分别进行拦截[1]。图1为多目标干扰示意图。

寻的导引头探测到多个目标时，主波束内有多个无法分辨的目标，因此，导引头接收到的是多个目标的合成回波，从而指向多目标能量重心位置。回波能量重心位置不断变化，导致导引头不断抖动，最终使导

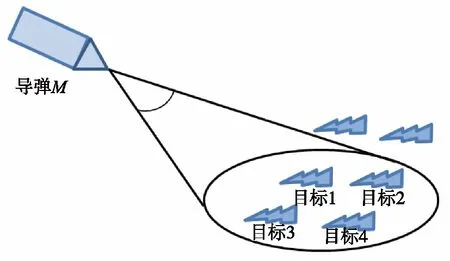
图1 多目标干扰示意图Fig.1 Diagram of multi-target interference

弹无法命中正确目标。目前，已有的对抗多目标干扰的研究成果主要是利用空间域、频率域、极化域的信息或直接采用信号处理技术去除多个目标之间的相关性等方法，但这些方法都需要发射和接收多个脉冲进行探测。脉冲间存在着一定的间隔时间，对于高速运动目标，不同脉冲探测到的目标会在下一时刻运动到不同位置，而相对位置一旦发生变化，就无法进行脉冲积累[2]。因此，在同一时间发送多个脉冲进行探测，是适用于高速运动多目标场景的方法。

在给出多目标环境下回波信号角度误差模型并分析其对寻的导引头角度跟踪影响的基础上，本文利用正交多载波技术，提出多目标干扰补偿方法，并通过仿真验证了该方法的有效性。

1 多目标分析

1.1 多目标环境下角度误差模型建立

假设被探测目标数为n，第j个目标的坐标为(xj,yj,zj)，第j个目标的雷达散射截面积为σj，与导引头相对距离最小的目标为导引头应跟踪的对象，其他目标为干扰。

在比幅单脉冲体制下，对多目标环境下的角度误差进行建模，并分析其对制导系统的影响。导引头和、差通道天线方向图的数学表达式可由式(1)～(2)表示[3]。

Σ(θ)=e-1.386(θ/θb)2

(1)

Δ(θ)=1.56·(θ/θb)·e-0.9(θ/θb)2

(2)

式中：θ为导引头电轴指向与真实目标指向的夹角，即测角误差；θb为导引头天线3 dB波束宽度。

根据文献[4]中给出的目标回波功率计算式，在多目标环境下，和、差通道输出的回波功率可由式(3)～(4)表示。

(3)

(4)

式中：j=1,2,…,n；n为目标个数，当n=1时，式(3)～(4)为单个目标的回波信号和、差输出；P为发射功率；θj为导引头指向与目标j指向的夹角；G为天线增益；λ为制导探测信号波长；σj为目标j的雷达散射截面积；dmj为目标j与导弹之间的距离；L为损耗因子；φj为目标j的回波信号相位。

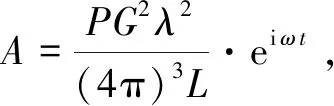
(5)

(6)

此时，导引头由于多目标产生的误差输出可表示为

E=Re[D/S]

(7)

1.2 影响分析

表1给出了多目标仿真参数，列出了多个目标的位置坐标。

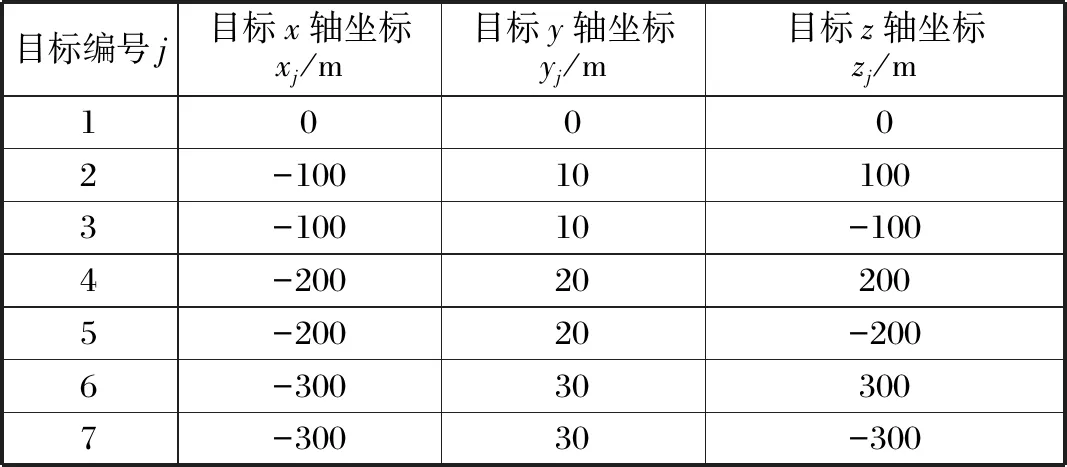
表1 多目标仿真参数表Tab.1 Multi-target simulation parameters

表1中的目标1与导引头距离最近，为导引头应跟踪对象，其他6个目标为干扰目标。

以表1的多目标仿真参数设置为例，假设所有目标的σj相同，将其代入式(5)～(6)，基于Matlab平台，可得出在末制导阶段不同目标指向和导引头实际指向的仿真比较图[5]，如图2所示。

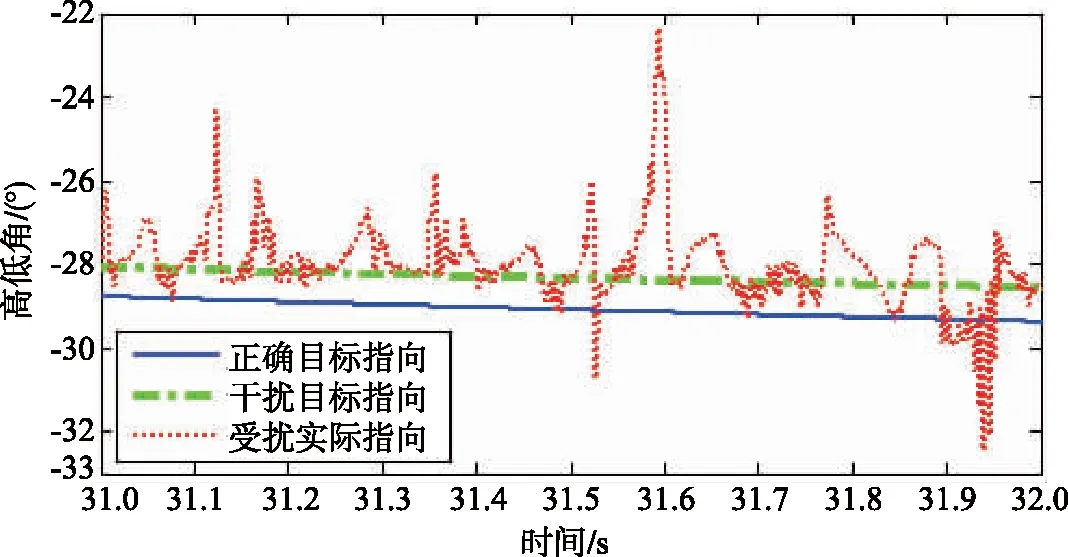
图2 多目标对导引头实际指向的影响Fig.2 The influence of multi-target on the actual direction of the seeker

图2中，横坐标为导弹飞行时间，纵坐标为导弹大地坐标系下的高低角。共有3条曲线，目标1为导引头应跟踪对象，蓝色实线即为导引头跟踪该对象的指向；绿色点划线为导引头跟踪某一干扰目标时(本文选择目标2)的指向；红色虚线为多目标环境影响下的导引头实际指向。由图2可见，在末制导阶段，由于受到多目标影响，导引头实际指向在各目标指向之间来回抖动，甚至会超出各目标指向。

2 基于正交多载波的抗多目标干扰技术

2.1 正交多载波技术

利用补码序列矩阵，正交多载波雷达信号同时调制生成多个满足正交关系的载波，模糊函数呈图钉型，具有高分辨力[6]，且可以与已成为诸多通信标准内容的正交频分复用技术有效结合，组建雷达通信网络[7]。文献[8]采用正交多载波技术，利用不同探测频点获得多个雷达误差值，建立多个方程提取多路径未知参量，实现多路径效应补偿。该技术在同一时间发射多个载波探测目标，所以适用于高速运动目标，其正交多载波雷达信号结构如图3所示。

图3 N×M的正交多载波信号结构Fig.3 N×M orthogonal multicarrier structure

N×M的正交多载波雷达脉冲信号，由N×M的补码矩阵同时调制N个相位周期为M×tb的载波生成(tb为单个相位周期)。载波间隔Δf为1/tb，载波间满足正交关系。单个正交多载波雷达脉冲信号可表示为

(8)

式中：

(9)

式中：Wn为各载波的幅度权重；φn,m为第n个载波的第m个相位元素。正交多载波脉冲具有tb/N的距离分辨力和1/Mtb的多普勒分辨力，脉冲压缩比达到N×M[9]。

2.2 干扰补偿原理

由式(7)可知，导引头雷达比幅单脉冲输出可由式(10)表达。

(10)

根据比幅单脉冲测角原理[10]，可得

Δ(θe)/Σ(θe)=Pe·θe

(11)

式中：θe为测角误差;Pe为导引头S曲线的误差斜率。

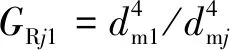
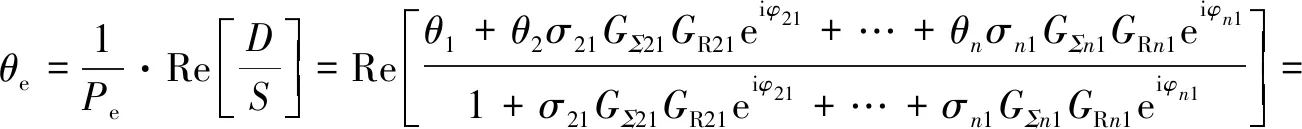
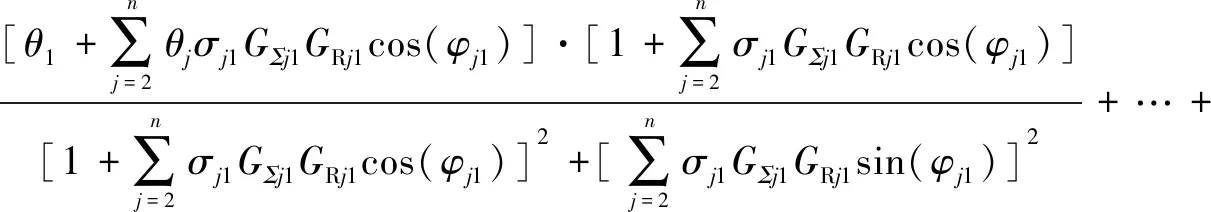
(12)

式中：干扰目标j与目标1的回波信号相位差可表示为

(13)

将载波频率f改变为f+Δf，可得各干扰目标相对于目标1的回波信号相位差为

(14)

相位差的变化量为

(15)

要实现多目标干扰补偿，需要求出θ1。由分析可知，角度误差输出方程中包含3n-1个未知量，分别为：n个误差角θj(j=1,2,…,n)；n个目标到导弹的距离dmj(j=1,2,…,n)；n-1个干扰目标与目标1的雷达散射截面积比值σj1(j=2,3,…,n)。通过调整载波频率f，可获得不同的角度误差输出方程，每个载波对应1个载频，使载波频率数N(即载波个数)为3n-1，可得到3n-1个方程，即可求解出θj，达到干扰补偿的目的。目标数n越多，补偿多目标干扰需要的载频数N也越多。

2.3 干扰补偿方法的简易实现

实际计算过程中，式(12)非常复杂，在工程上难以实现。为此，可采用以下简易实现方法。

根据式(5)，调整载波频率f，可得回波信号和通道输出为

(16)

假设Δφj1max=2π，且在0～2π范围内，Δφj1max均匀分成与载波个数相同的N个相位差值，即每调整一次载波频率，相位差改变2π/N，将所有的和通道信号输出相加，可得

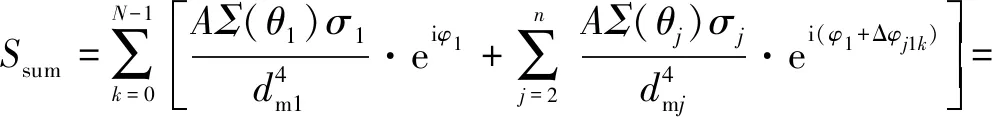
(17)

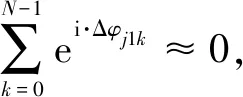
(18)

同理，将所有差通道信号输出相加，可得

(19)

补偿后的雷达误差输出可表示为

Ecomp=Re[Dsum/Ssum]≈Re[Δ(θ1)/Σ(θ1)]

(20)

各干扰目标相对于目标1的回波信号相位差变化最大点Δφj1max=2π，可得

(21)

由此可得载波频率最大变化量，即频率跳变带宽需求为

(22)

式中：c为光速，c=3×108m/s。

均匀分布的载波频率变化间隔为

(23)

3 补偿效果仿真分析

3.1 仿真结果

根据上文的角度误差模型及表1的多目标模型，采用不同载频数N进行多目标干扰补偿，图4为在末制导阶段，目标1指向、干扰目标指向、导引头实际指向及使用本文方法补偿后导引头实际指向的仿真比较。

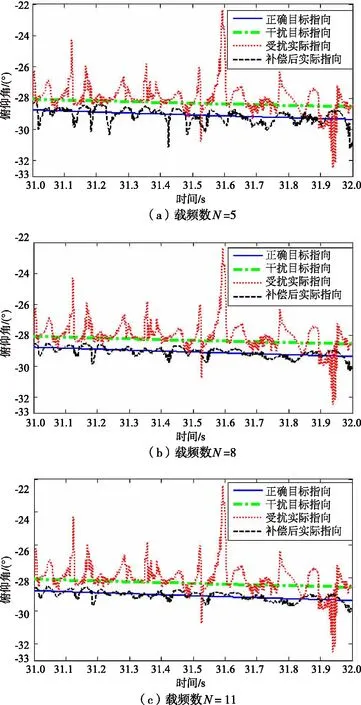
图4 不同载频数多目标补偿效果图Fig.4 Multi-target compensation effects with different carrier frequency numbers

3.2 结果分析

与图2相比，图4多出一条黑色虚线，黑色虚线表示采用本文补偿方法后导引头的实际指向。由图4可知，经本文方法补偿后的导引头实际指向明显比未经本文方法补偿的导引头实际指向抖动小很多，导引头角度跟踪受多目标的干扰减少很多。当载频数N=5时，由于没有获得足够的相位点数，干扰目标回波功率无法完全抵消。随着载频数N的增加，跟踪目标回波功率积累增加，干扰回波功率基本被抵消，N=8时可较好地实现多目标干扰补偿。本文采用固定RCS目标进行仿真，采用RCS起伏模型时，也可达到较好补偿效果。

4 结束语

受多目标干扰的影响，寻的导引头实际指向在各目标指向间来回抖动，甚至会超出各目标指向。基于正交多载波体制，可在同一时刻利用不同探测频点获得多个角度误差输出方程，提取出多目标未知参量，实现多目标干扰补偿。不同探测频点下，不同目标的回波信号存在相位差，合理选取探测频点，可抵消干扰目标回波信号，简易实现多目标补偿。由以上分析和仿真结果可知，不同载频数N对多目标补偿有影响，载频数N越大，补偿效果越好。本文补偿方法采用固定带宽进行，在后续研究中，可以考虑采用自适应带宽进行角度干扰补偿。