防空作战火力资源优化分配研究

吴 凯,徐 利，孙海涛

(1. 上海机电工程研究所，上海 201109； 2. 上海航天电子技术研究所，上海 201109)

0 引 言

随着武器系统的不断优化升级和高科技作战手段的不断更新，战场环境日趋复杂，现代地面防空作战面临更多的挑战。为了充分发挥防空武器系统的作战效能，防空部队往往采用多型杀伤性导弹武器梯次配置对目标进行多层防御。如何充分发挥火力单元的整体协调优势，为防御来袭的多个目标合理分配火力资源，提出最优的分配方案，实现多火力单元的协同打击，提高作战效能，是防空作战的一个重要研究方向，也是一个亟待解决的基础问题[1]。

火力分配问题是一个约束众多且复杂的组合优化问题，属于NP(non-deterministic polynomial，多项式复杂程度的非确定性问题)完全问题，目前尚未找到求其多项式最优解的算法。随着来袭目标数目和火力单元数的增加，其解空间上呈现指数型增长的趋势，解算过程会耗费大量时间。因此，对于较大规模的火力分配问题，在实际允许的时间内求解其最优解是不现实的，只能根据假设的作战原则求其满意解。由此可见，求解NP问题的核心是改进求解算法，使其在短时间内能够得到满意的火力资源分配方案[2]。

求解火力资源分配问题的算法，分为传统算法和智能优化算法。传统算法主要有分支定界法、隐枚举法、动态规划法、割平面法等；智能优化算法主要有遗传算法、模拟退火算法、神经网络算法、蚁群算法、粒子群算法以及混合优化策略等。传统算法较为简单，但编程实现时较为繁琐，且当目标数增多时，收敛速度较慢，仅适用于处理简单的作战任务分配[3]。

1 火力资源分配模型建立

建立一个真实、可行的火力资源分配模型是获取解决方案满意解的第一步，也是最重要的一步。若分配模型太简单，就不能贴合实际的作战需求；分配模型太复杂，则易导致解算耗时太长且不易求得满意解。因此，应该合理地选取火力资源分配方案中的主要影响因素和效能指标，以有效地控制分配模型的复杂程度[4]。

假设多火力拦截组成的防空系统配置如下：共有m类导弹武器发射平台，每类发射平台只装备同一种导弹；空中来袭目标总数为n个；第i类武器发射平台所装备的第i种导弹数量为li(i=1,2,3,…,m)枚；第j个目标的威胁值为Wj(j=1,2,3,…,n)；pij为第i种导弹对第j个目标的杀伤概率；xij是用于拦截第j个目标的第i类导弹武器的数量。

第i类平台对第j个目标的杀伤概率为

Pij=1-(1-pij)xi j(j=1,2,…,n)

(1)

所有m类导弹对第j个目标的杀伤概率为

(2)

常用的火力资源分配模型为

(3)

为了合理运用现有的火力资源，充分发挥整体优势，在取得对目标杀伤概率最大平均值的基础上，尽可能减少火力资源消耗，确保在后续增援目标到达时有充足的火力资源对其实施打击，采用如下改进型的带有杀伤概率阈值的火力资源分配模型[5]。

(4)

式中：Pdj为对第j个目标预设的杀伤概率阈值，其数值可根据战场空情态势灵活设定，也可由上级指控系统指定。

该火力资源分配模型具有如下特征：

1) 只有当对目标的杀伤概率大于预设的杀伤概率阈值时，该目标才有可能被分配火力资源。

2)Wj可以使高威胁度的目标在分配时具有较高的优先级。

因此，在满足对目标杀伤阈值的基础上，通过综合评估杀伤概率和火力资源消耗，该算法可以高效费比实现对多目标的高效打击。

2 火力资源分配算法设计

2.1 基本遗传算法

1) 算法流程

遗传算法作为一种实用高效、鲁棒性强的优化技术，提供了求解非线性、多目标模型等复杂系统优化问题的通用框架，是一种看似没有规律却能够在遗传变异中筛选出适合全局最优解的仿生智能算法[6]。

在对来袭目标分群的基础上，遗传算法利用其全局寻优的优势，在搜索过程中自动获取和累积有关搜索空间的知识，并自适应地控制搜索过程，通过有组织而又随机的信息交换来重新结合那些适应性好的串，生成新的适应性好的串的群体。为了保证时间性能，遗传算法不一定能得到最优解，但是可以找到次优解或满意解，与来袭目标进行配对[7-8]。

一个完整的基于遗传算法解决火力分配问题的流程如图1所示。

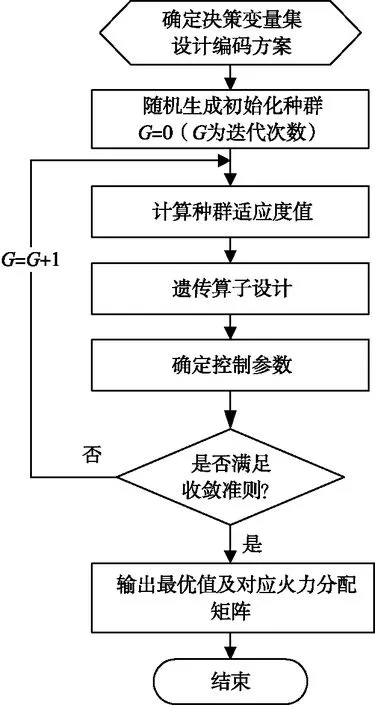
图1 基于遗传算法的火力资源分配Fig.1 Fire resources assignment based on genetic algorithm

2) 算法参数选择

遗传操作中的相关参数一般根据以下原则进行选取[9]。

① 种群规模S。种群规模对算法的效率有明显影响。S太小时难以求出最优解或根本找不出问题的解，因为太小的种群规模不能提供足够的采样点；S太大则会使收敛时间延长。一般S取20～160。

② 交叉概率Pc。此参数控制着循环中交叉操作的概率。Pc太小时搜索会停滞不前；Pc太大会使高适应值的结构很快被破坏掉。一般Pc取0.60～0.95。

③ 变异概率Pm。它是增大种群多样性的第二因素，是从个体群中产生变异的概率。Pm太小时难以产生新的基因结构；Pm太大会使GA(genetic algorithm，遗传算法)变成单纯的随机搜索。一般Pm取0.01～0.20。

④ 适应度函数。也称为评价函数，是根据目标函数确定用于区分群体中个体好坏的准则，是算法进行自然选择演化的唯一依据。适应度函数总是非负的，其数值越大越好。适应度函数可按式(5)直接从待求解的目标函数转换获得。

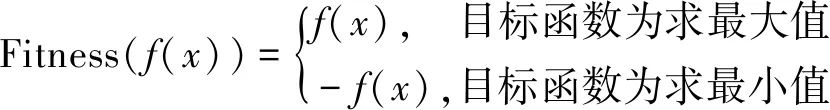
(5)

2.2 算法设计

1) 算法优化

在基本遗传算法的基础上，为了防止每次进化中选择、交叉、变异等遗传操作破坏当前种群中适应度最好的染色体，影响算法的收敛和运行效率，采用最优保持策略。只对除最好适应度以外的个体进行遗传操作，而将最好适应度的个体直接复制到下一代。

为了改进遗传算法性能，采用自适应遗传算法进行火力资源分配。主要通过衡量适应度值自适应改变交叉概率和变异概率，以求得相对某个解的最佳交叉概率和变异概率。自适应遗传算法中的交叉概率和变异概率计算模型为

(6)

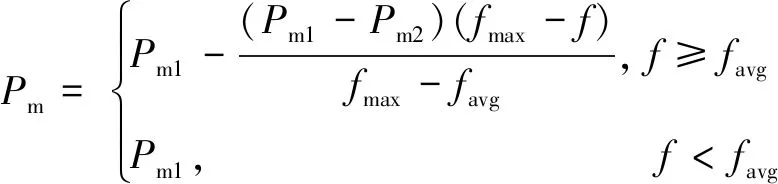
(7)

式中：fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;f′为所要交叉的两个个体中较大的适应度值;f为所要变异的个体的适应度值。

同时，为了增加种群的多样性，在自适应遗传算法中引入了多位变异的思想。当通过自适应方法产生变异概率后，如果最大适应率等于最小适应率，则只对选中个体的一个位置进行变异，否则，随机对选中个体的多个位置进行变异。

2) 编码方案

根据火力资源分配模型和改进遗传算法，采用二进制编码方案把火力资源分配模型的解作为染色体进行编码。设有r个目标，t个不同的火力单元，则编码后的完整染色体可表示为

X=(x11,x12,…,x1r,x21,x22,…,x2r,…,

xi1,xi2,…,xij,…,xir,…,xt1,xt2,…,xtr)

3) 适应度函数

初始种群是随机生成的，种群中的染色体可能不满足约束条件或越过上边界而无遗传价值。对于不满足约束条件的染色体，采用大幅降低其适应度值的方法进行惩罚。惩罚的作用是保护有效染色体，破坏无效染色体(充分降低其遗传概率)。据此，将适应度函数设为

(8)

式中：X为染色体的完整编码方案，也是目标函数的解。

3 仿真实例

假设某区域防空阵地部署有6个不同型号地空导弹的不同火力单元，用于协同防御，各火力单元配置的地空导弹数量分别为[5,3,4,6,2,5]；在该区域内发现有5个来袭的空中目标。为了便于问题分析，假定1个火力单元对1个目标只发射1发导弹进行拦截。

来袭目标对该阵地的威胁系数以及不同火力单元对各个目标的杀伤概率分别如表1和表2所示。按照上级指控要求，对各个目标的杀伤概率阈值Pd设为不低于0.9。设置种群规模S=50，交叉概率Pc1=0.9，Pc2=0.6，变异概率Pm1=0.1，Pm2=0.001。

表1 目标威胁系数Tab.1 Target threat coefficients

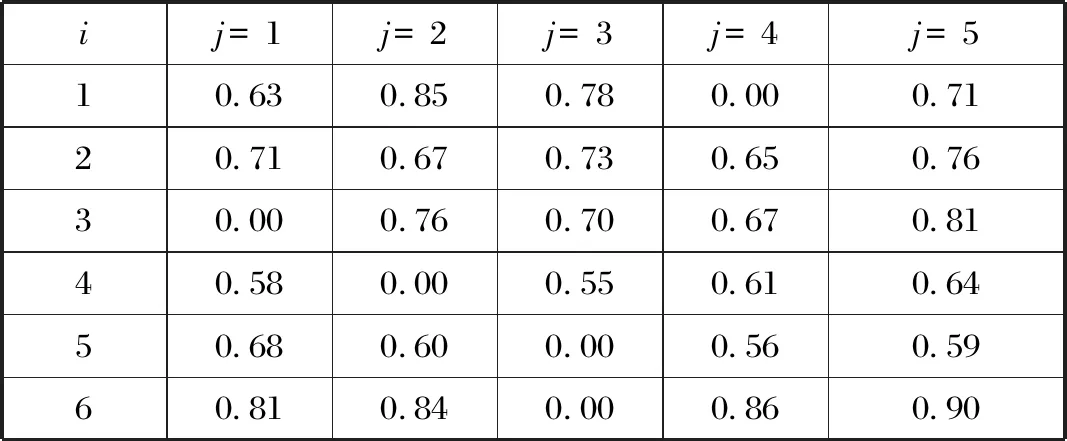
表2 火力单元-目标杀伤概率Tab.2 Fire unit-target kill probability

基于上述火力资源分配模型，使用基本遗传算法和自适应遗传算法进行火力-目标分配仿真，得出的适应度随迭代次数的变化如图2～3所示。

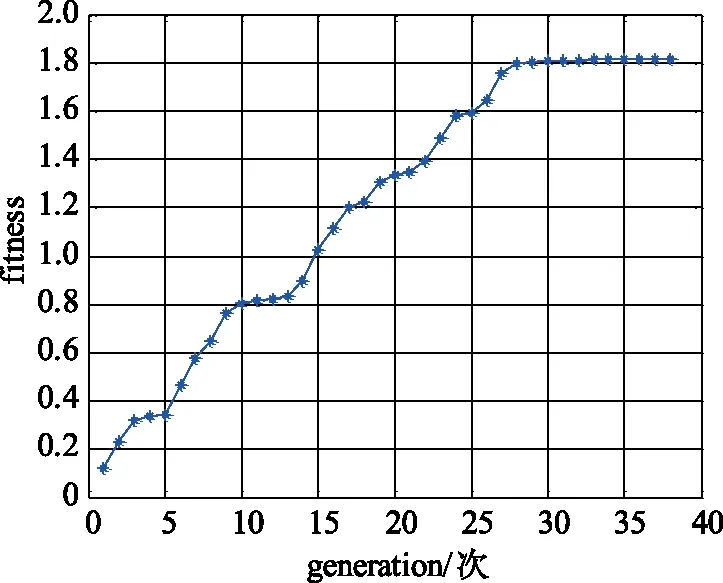
图2 基本遗传算法适应度Fig.2 Fitness of basic genetic algorithm

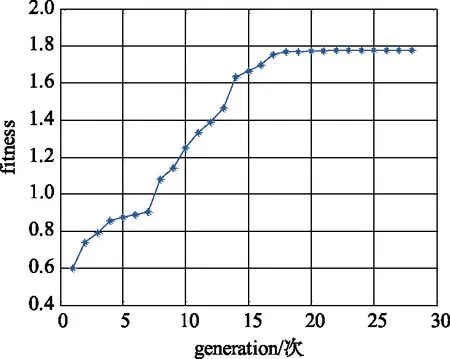
图3 自适应遗传算法适应度Fig.3 Fitness of adaptive genetic algorithm

从以上仿真结果的对比中可以看出，基于改进的火力资源分配模型，在满足设定的杀伤概率阈值的前提下，相比基本遗传算法，自适应遗传算法有更强的爬坡能力和更快的收敛速度，为战场决策赢得宝贵的时间资源。

4 结束语

目标与火力资源分配作为作战辅助决策中的核心内容，在现代防空作战中起着至关重要的作用。本文针对防空导弹火控系统中的火力分配问题进行了研究，建立了防空作战火力分配数学模型，并在此基础上采用了一种优化改进的自适应遗传算法。通过仿真实例证明该算法相比于基本的遗传算法可加快优化搜索的速度，有效避免算法陷入局部最优陷阱，为改进区域多目标火力资源分配提供了一种新的解决方案。