例析设未知数在生物解题中的应用
安徽
设未知数来解决问题是数学学科常用的方法,同样在生物解题中也有应用,下文以三个实例来解析其具体的应用。
1.设未知数在判断显隐性上的应用
1.1 例题呈现
玉米胚的性状有粉质型、甜粉型、甜质型三种,分别受等位基因A1、A2、A3控制。某兴趣小组种植一株粉质型和一株甜质型(有自交也有杂交),并将所得种子全部种植,粉质型所结种子种植有粉质型和甜粉型,而甜质型植株后代有三种类型,求三个等位基因的显隐性关系及亲本粉质型的基因型。
1.2 “口诀型解法”及对其的反思
有人认为,玉米为同株异花植物,在甜质型植株上产生了三种后代,所以甜质型为最隐性(A3),亲本粉质型后代有粉质型与甜粉型,故其两种配子为A1、A2,则显隐性关系为 A1>A2>A3。
该方法看起来简单明了,但是口诀是怎样总结出来的以及口诀中的因果关系是否正确尚无法得知。用假设-反证法来进行验证,假设以上结果为正确的,则若有如下的两植株: 粉质型(A1A2)、甜粉型(A2A3),它们既自交又杂交,甜粉型个体后代有 A2、A3A3、A1三种类型,如根据解题口诀“三种都出现为最隐性”则有显隐性关系A1>A3>A2,结论与假设又不一致,可见口诀是错误的,解题“成功”具有很大的偶然性。
1.3 设未知数进行推理论证
已知粉质型中必然含有A1基因,甜质型中必然含有A3基因,后代中共有三种类型,则在这两种类型的植株中必然含有A2基因,假设1:A2基因在粉质型植株中,则可得两植株的基因型为A1A2、A3X(X为未知基因);假设2:A2基因在甜质型植株中,则可得两植株的基因型为A1X(X为未知基因)、A3A2。
对于假设1,由粉质型基因型A1A2可知,A1相对于A2为显性,即A1与A2的显隐性关系是A1>A2,其后代有A1A1、A2A2、A1A2、A1A3、A2A3、A1X、A2X,因其中只有粉质型和甜粉型两种表现型,故对已确定基因型的表现型进行归类可得,粉质型为A1A1、A1A2、A1A3;甜粉型为A2A2、A2A3,由此可知A2显性强于A3,即A2与A3的显隐性关系是A2>A3,则三者的显隐性关系可表达为A1>A2>A3。A1X、A2X属于这两种表现型,故理论上X是A1或A2或A3都不影响结果(亲本后代有粉质和甜粉两种表现型),但亲本甜质型植株为A3X,则X只能是A3,即甜质型个体为A3A3,其后代为A3A3、A1A3、A2A3三种基因型,分别体现为三种表现型。故假设1的推理结果在逻辑上没有问题。
对于假设2,由甜质型基因型A3A2可知A2与A3的显隐性关系是A3>A2,粉质型的后代有A1A1、A1X、XX、A1A3、A1A2、A3X、A2X,后代无甜质型,故可得 A1>A3,则有A1>A3>A2。对已知类型的表现型进行归类得粉质型为A1A1、A1X、A1A3,后代共有粉质型和甜粉型两种表现型,故X不为A3(若为A3,则A3X、A2X表现为甜质型),X也不为A2(若为A2,则A3X表现为甜质型),故X只能是A1,则XX 、 A3X、 A2X皆表现为粉质型,即粉质型杂交和自交的后代全为粉质型,又与题意相悖,故假设2错误。
综合假设1、2可知正确答案为显隐性关系A1>A2>A3,粉质型个体基因型为A1A2。
2.设未知数在植物生长素问题上的应用
2.1 例题呈现
若某受到单侧光照射的胚芽鞘向光弯曲生长,尖端向光侧生长素浓度如图1中A点所示,求背光侧生长素的浓度。
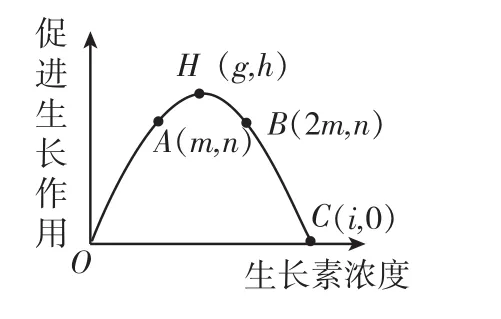
图1
2.2 设未知数以函数的形式解题
可将该曲线认为是一个表示生长素浓度(x)对植物生长促进作用(y)的相关函数,则有y = f(x)。设背光侧浓度为 a,则有向光侧浓度关系函数 y1= f(m)= n;背光侧浓度关系函数 y2= f(a);
背光侧浓度大于向光侧(横向运输导致),即a>m,且背光侧生长快于向光侧,即f(a)>f(m)= n,结合曲线可知大于A点而小于B点,即位于两者之间的浓度,得范围m<a<2m。
实际上该题有很多种解法,但相对而言,设未知数以函数的形式解题,思路更加清晰,也足够的理性,结果更令人信服。
3.设未知数在求解质粒长度上的应用
3.1 例题呈现
如图2为某种常用质粒的序列图,图3为目的基因的序列及其相关限制酶的识别序列。请回答下列问题:
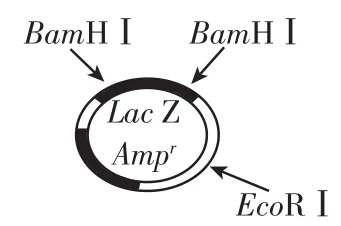
图2
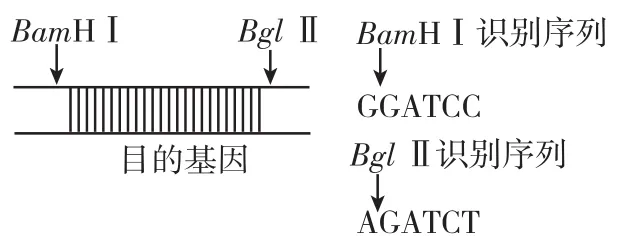
图3
将若干个质粒和目的基因用BamHⅠ和BglⅡ两种限制酶切割后,用DNA连接酶相连,然后再用BamHⅠ和EcoRⅠ切割成功连接后的产物,获得了长度为0.7 kb、2.8 kb、1 kb和2.5 kb四种长度的DNA片段,则目的基因的长度为______kb(已知目的基因的长度大于1 kb)。
3.2 设未知数进行求解
分析题意可知,质粒上的两个BamHⅠ酶切位点可与目的基因上的BamHⅠ和BglⅡ酶切末端连接,但是BamHⅠ末端和BglⅡ末端连接后原酶切位点消失(由—GGATCC—变成了—GGATCT—),即不能再为BamHⅠ酶所识别切割,此时只剩下两个酶切位点——BamHⅠ和EcoRⅠ,设目的基因长度为a,对于重切割后的质粒长度做以下分析:
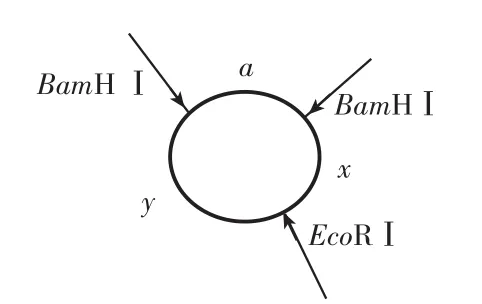
图4
由图4分析可知,重组后三段序列的位置关系,从生成的四种片段长短关系可推知质粒加目的基因总长度为3.5 kb,即 0.7 kb与2.8 kb 为一组,1 kb与 2.5 kb 为另一组,产生不同组合的原因是BglⅡ末端连接顺序不同导致的,则有以下数量关系:
若BglⅡ末端与左上的BamHⅠ末端相连接则有:
(1)a+y = 2.5,x = 1或a+y = 2.8,x = 0.7
若BglⅡ末端与右上的BamHⅠ末端相连接则有:
(2)a+x = 2.8,y = 0.7或a+x = 2.5,y = 1
组合得以下方程组:

则无论是哪组数据解得a=1.8 kb 。
由以上几个例子可知,设未知数在生物学上的应用并不仅是数学计算方法的运用,而是将未知的参数具体化,便于结合生物学知识方法用以具体的判断或比较,使学生头脑在思考问题时从模糊的“云”思考转变为条理清晰的推理论证,使学生能知其所以然,而并非仍在“云雾”中。
——一道江苏高考题的奥秘解读和拓展

