基于电流变化规律的PMSM初始位置检测方法

彭皆彩，王 宾，董永刚

(1.安徽理工大学，淮南 232001； 2.邢台职业技术学院，邢台 054000)

0 引 言

永磁同步电机(以下简称PMSM)转子初始位置角的准确检测影响着电机的起动以及正常工作中的控制性能[1]，如果不能准确获得转子初始位置角，可能会导致起动失败，电机反转甚至过流损坏设备等严重后果[2]。因此，国内外研究人员对PMSM转子初始位置检测做了大量研究。

文献[3]提出一种基于电压矢量注入的PMSM初始位置角检测方法，通过比较电流响应的大小判断转子位置，在接近转子实际位置时，增大注入电流，以增大差异性。该方法易造成转子转动，且当转子处于某些特定位置时分辨率不够；文献[4-6]采用高频信号注入的方法，通过对高频电流响应进行处理，采用拟合算法或者位置观测器，获取转子初始位置，方法中包含有数字滤波器、位置观测器，数据运算量大，且算法执行时间较长。

文献[7]提出一种基于检测电机瞬态电流响应的脉冲电压矢量注入方法，该方法以电感差异为基础，但不适用于表贴式PMSM；文献[8]提出了一种基于线电感变化特征的PMSM初始位置检测方法，需测量电机线电感，不具有通用性，实现复杂；文献[9]提出一种电流差值检测方法，该方法计算得到的电流差值，实际叠加有二次、三次谐波分量，直接用于转子初始位置计算，存在较大误差。

针对上述存在的问题，本文分析了基本电压矢量作用下电流响应的变化规律，研究了一种对脉冲电流响应累加的方法，计算转子初始位置角。本方法不需要大量数据运算，实现算法简单，精度高，工程实用性较高。

1 定子电感的饱和效应

为了提高空间利用率，PMSM总是设计成主磁路的某些部分有一定的饱和度，因此，在考虑永磁磁极磁势及相绕组磁势对绕组饱和度的影响时，相绕组自感与相绕组间互感的大小将随转子位置变化而变化[10-11]。

图1中，d为永磁体磁极的轴线方向，a，b，c为A，B，C相绕组的轴线方向，θ为转子位置角。绕组电感饱和效应具体分析如下：

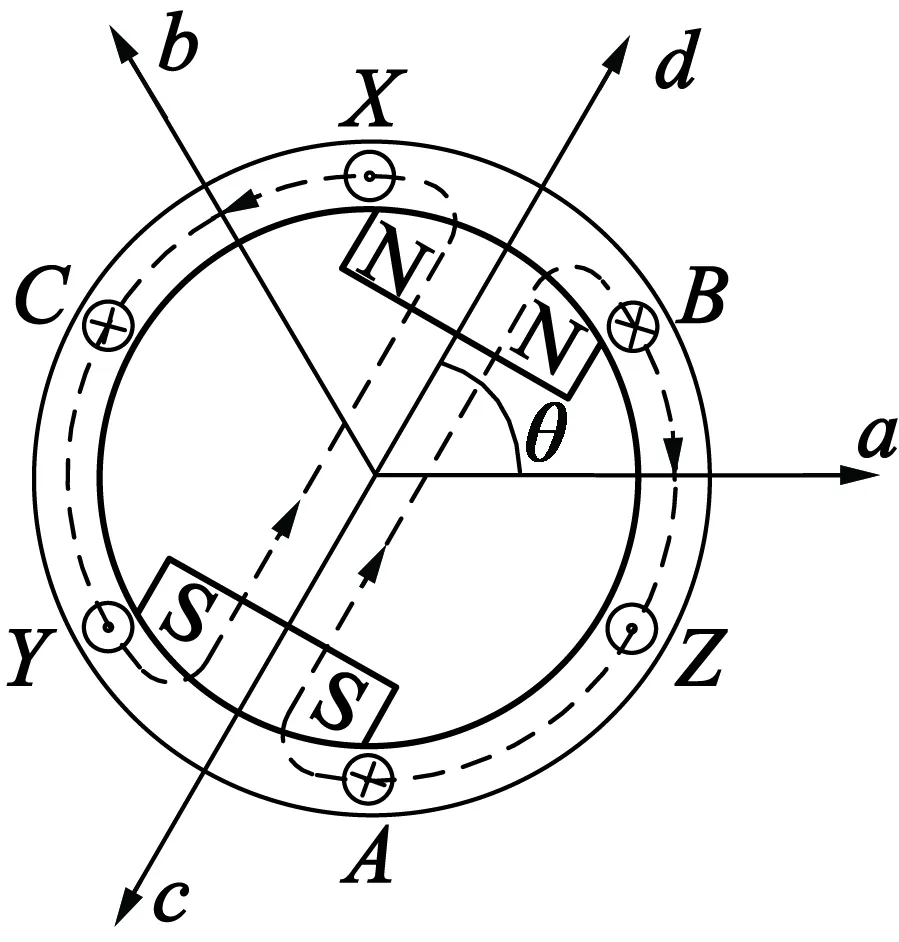
(a) iA=0时

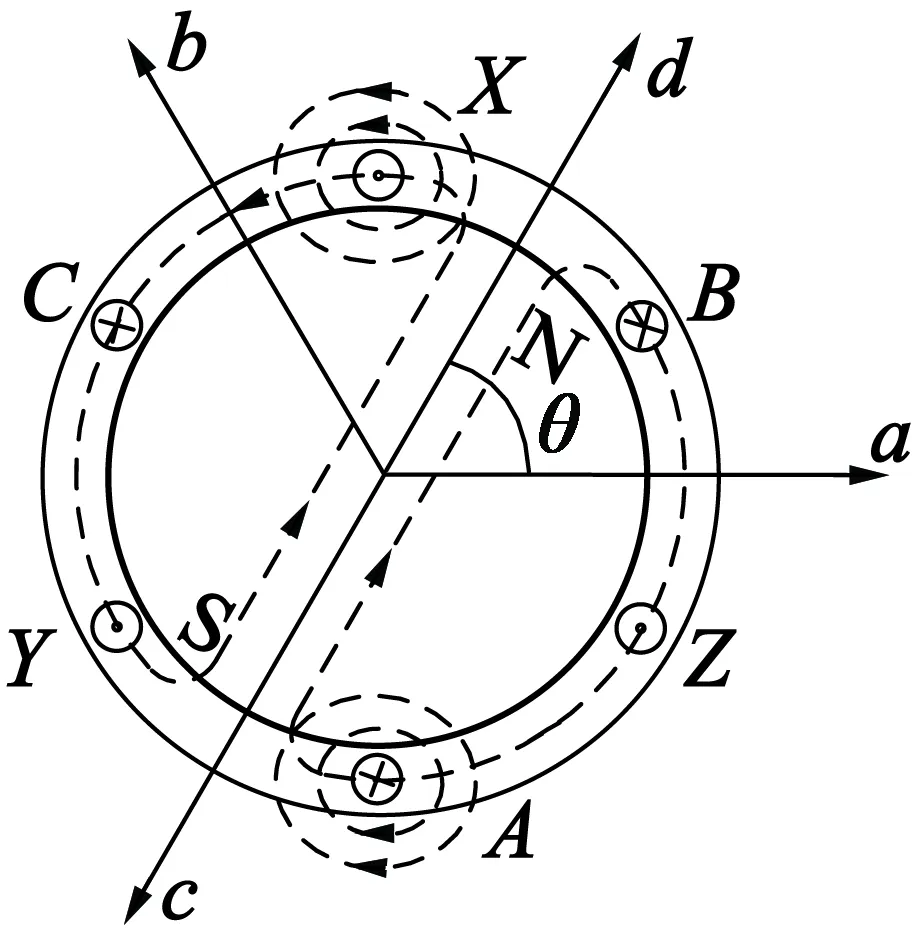
(b) iA>0时

(1)如果不考虑永磁磁动势和绕组电流产生的磁动势影响，绕组电感应为恒定常数，电感的变化曲线如图2中L1曲线。

(2)仅考虑转子永磁体磁通的影响，相绕组电流为0时，转子磁通如图1(a)所示。以A相绕组为例，当θ=0和θ=π，A相绕组通过的转子磁通最多，此时饱和度最高，电感值最小；当θ=π/2和θ=3π/2，A相绕组与转子磁通正交，此时饱和度最小，电感值最大。仅考虑永磁体磁通的影响时，电感的变化曲线如图2中L2曲线，除常数分量外，主要还叠加一个二次谐波分量。

(3)考虑定子绕组磁通的影响，相绕组电流不为0时，绕组磁通与永磁体磁通共同作用，影响相绕组磁路状态。当A相电流iA> 0时，A相绕组磁通如图1(b)所示，当θ=0，绕组磁通与永磁体磁通同向，起增磁作用，A相磁路饱和度增加，电感减小；当θ=π，绕组磁通与永磁体磁通反向，起去磁作用，A相磁路饱和度降低，电感值增大；当θ=π/2和θ=3π/2，绕组磁通单独作用在A相磁路上，它的值一般不足以使A相磁路达到饱和状态，则A相电感仍然保持较大的不饱和值。当A相电流iA< 0时，绕组磁通对电感的影响与iA> 0时完全相反，即在θ= 0时，电感增大，在θ=π时，电感值减小。考虑绕组磁通和永磁体磁通共同影响时，电感变化曲线如图2中L3线 (iA< 0)和L4线(iA> 0)所示，除平均分量及二次谐波分量外，分别叠加有基波分量。

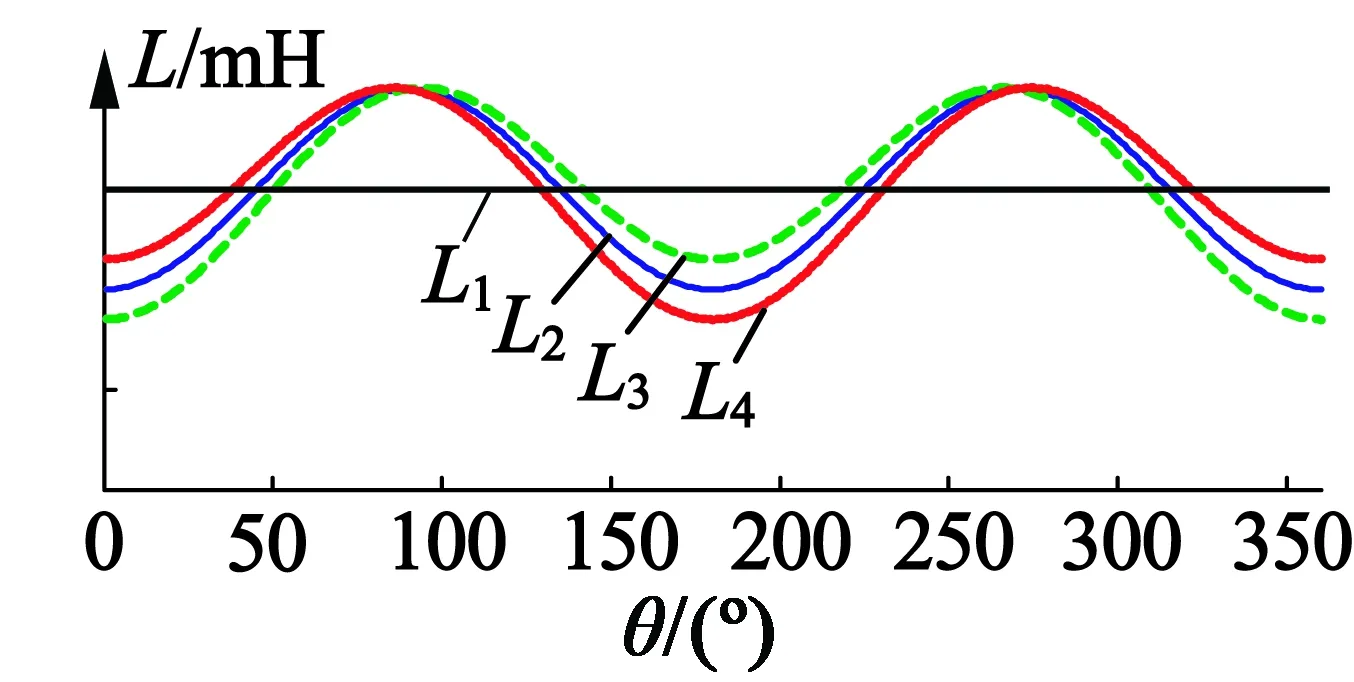
图2 电感变化曲线

由上述分析可知，电感值L随转子位置θ的变化规律包含有转子位置角信息。处于静止状态的PMSM，其定子绕组可以等效为电阻电感串联电路，则电路零状态响应：

(1)

由式(1)可知，电路的零状态响应包含有转子位置角θ。因此，对电机绕组施加6组基本的开关管导通组合，即施加基本电压矢量，可获得6组电流响应数据。其中包含有转子位置角随电流响应的变化规律，可从电流响应中提取出实际的转子位置角。

2 实验测量及数据分析

为了深入分析定子绕组电流响应与转子位置的对应关系，对一台8对极表贴式三相PMSM(样机)做测量实验。

表1 电机基本参数

2.1 实验系统介绍

图3为实验系统拓扑图。其中，Q1～Q6为开关管，D1～D6为开关管反并联的二极管，UDC为母线电压，C1为母线电容，在电机A，B两相中串接精密电流取样电阻R1，R2，再经过线性光耦，以隔离的方式将A，B相电流信号变换成电压信号，放大后再进行采样，处理器采用TI公司的TMS320F28035芯片。

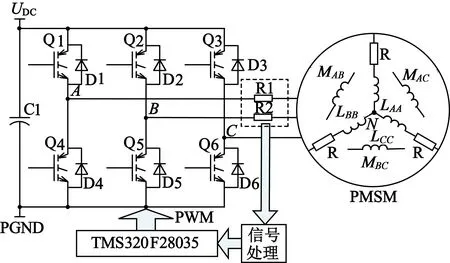
图3 PMSM三相全桥驱动拓扑示意图

2.2 测量流程

对处于静止状态的三相PMSM施加图4中的基本电压矢量。

首先对三相桥施加V1(100)，A相电流流入，B，C相流出，施加结束时检测A，B，C三相电流值iA1，iB1，iC1，并记录；然后关断Q1～Q6，电机定子绕组线圈中电流通过二极管D2，D3，D4流出，使A，B，C三相电流值降为零。

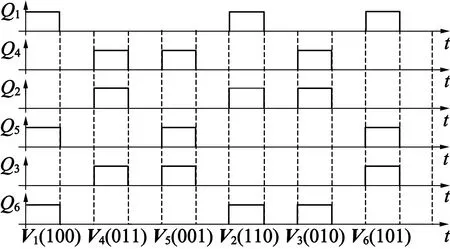
图4 基本电压矢量施加时序

按照图4时序，重复上述步骤，施加V1，V4，V5，V2，V3，V6，共测量得iA1～iA6，iB1～iB6，iC1～iC6。电压矢量作用后，A相电压采样波形如图5所示。

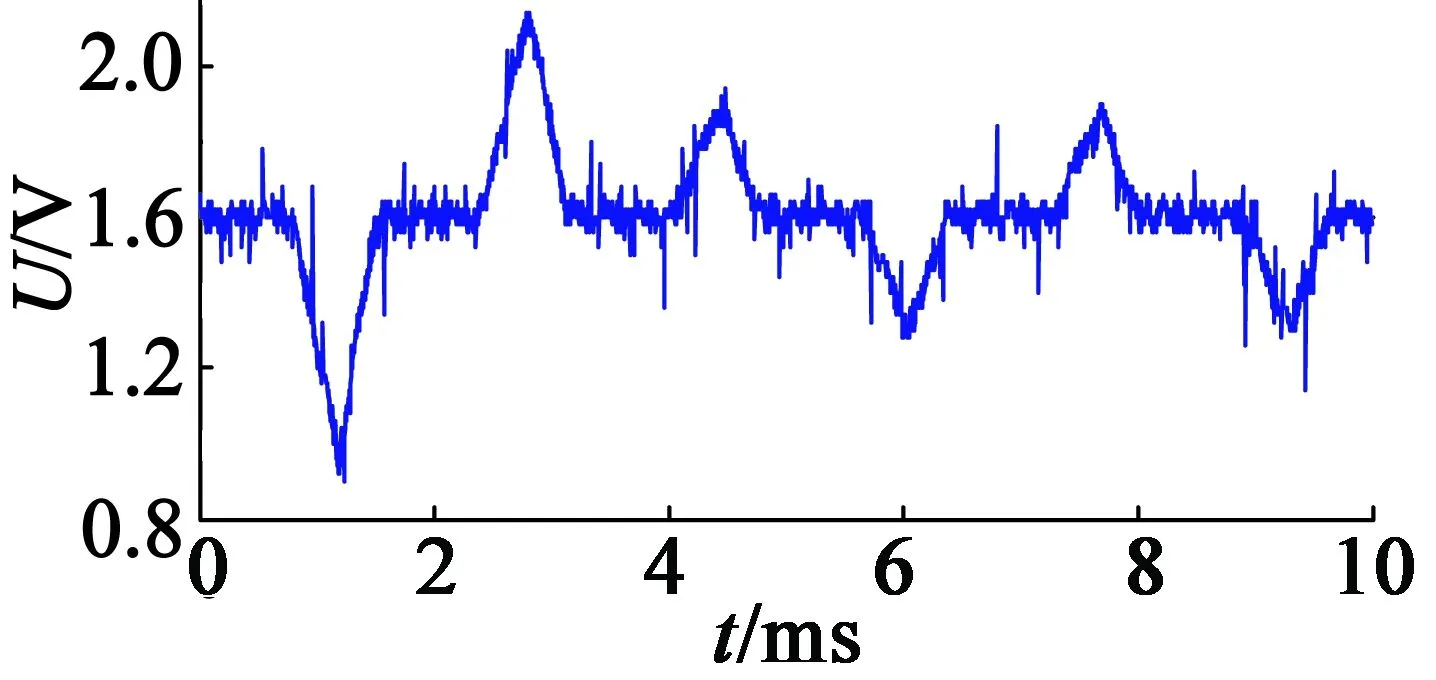
图5 A相采样波形

2.3 电流响应分析及初始位置估算

为获得整个周期中相电流响应的变化规律，将电机一个电周期分为100份，每隔3.6°执行一次上述测量流程，并记录各相的电流响应数据。将测量所得的A，B，C相电流响应数据绘制成图6。

图6中iA1(θ)～iA6(θ)，iB1(θ)～iB6(θ)，iC1(θ)～iC6(θ)曲线分别为在一个电周期内依次施加电压矢量V1,V4,V5,V2,V3,V6得到的A，B，C相电流波形。

以A相为例进行数据规律分析，首先对A相的6组电流数据做傅里叶级数分解，其中主要包含直流分量、基频、二倍频及三倍频分量。忽略三次以上谐波，对A相iA1(θ)～iA6(θ)电流数据做信号重建，表达式如表2所示。

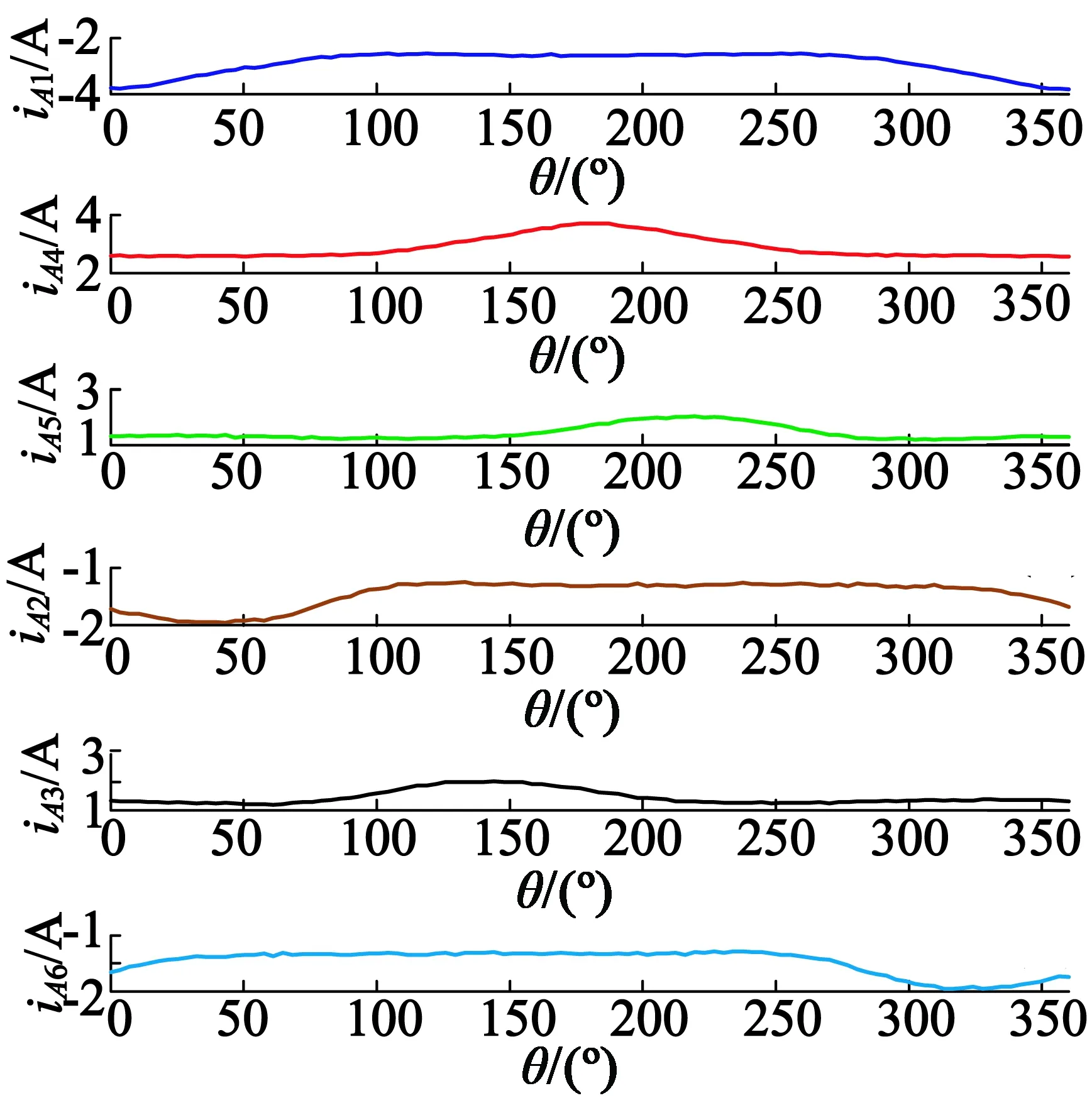
(a) A相电流响应

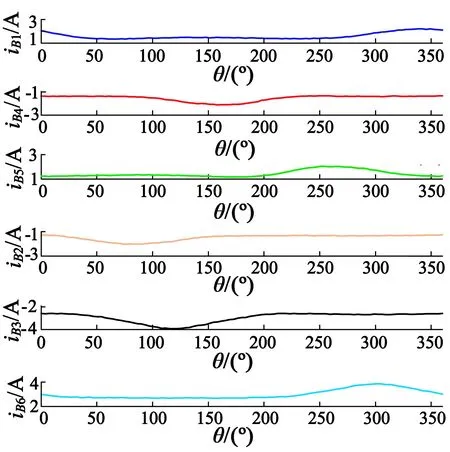
(b) B相电流响应

表2 A相电流表达式

将表2中重建的6组电流数据中的基频、二倍频及三倍频分量分别绘制成向量图，如图7所示。

(a) 基频向量

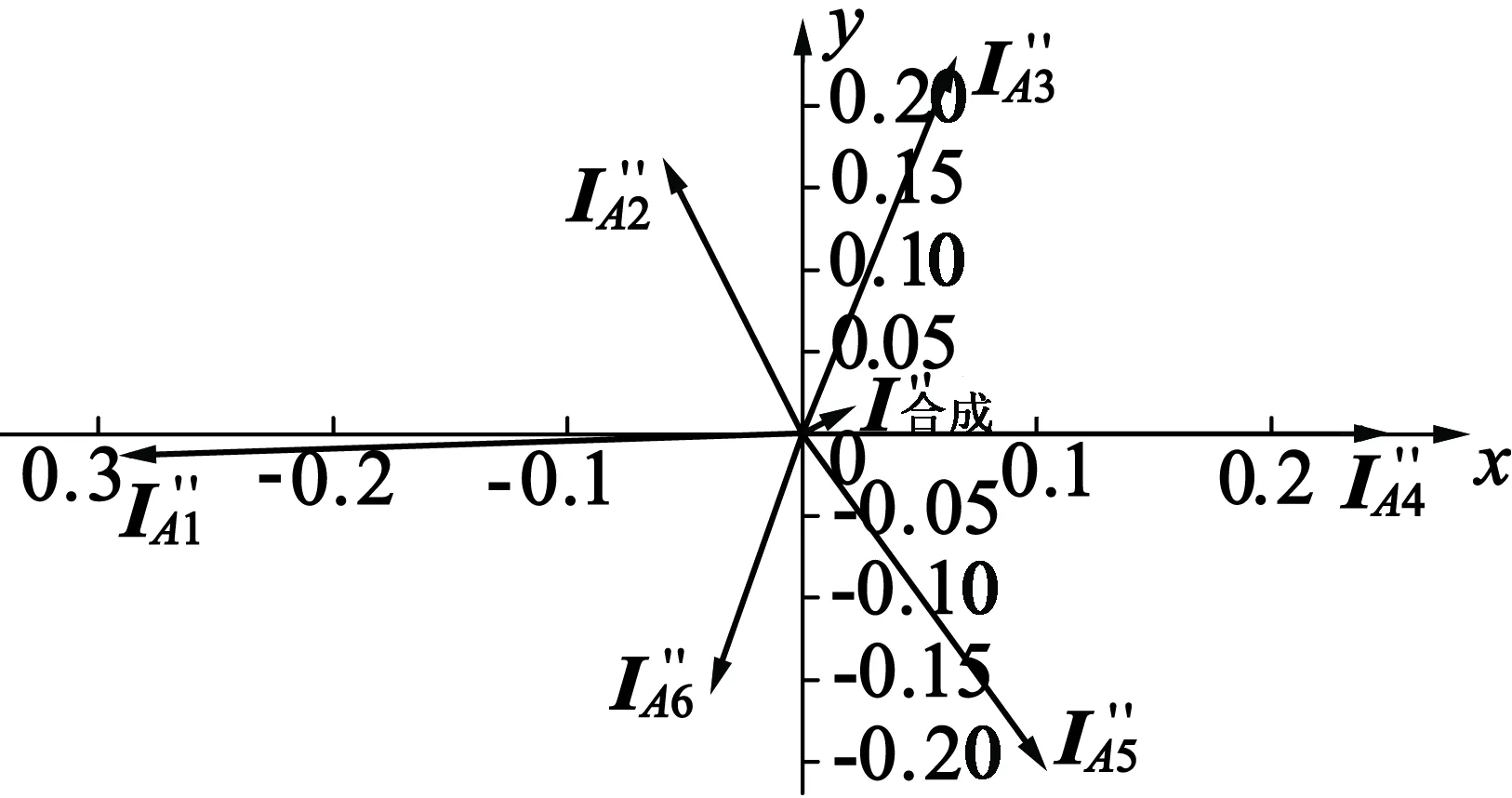
(b) 二倍频向量

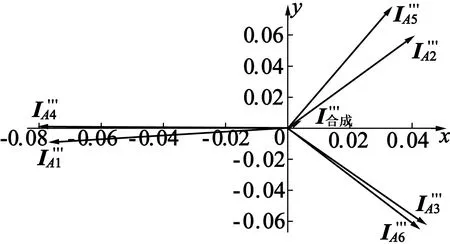
(c) 三倍频向量

将一个周期中获取的A，B，C三相的电流数据分别做信号重建，数据累加处理。同时，将各相的原始电流数据直接累加处理。将两种处理方式获得的数据绘制如图8所示。

由图8可知，电流数据直接相加所得波形与信号重建波形相比，波形频率相同、幅值相同，且各相初相位互差120°，做三相正弦规律变化，完全符合向量分析的结果。因此可假设iAS(θ)，iBS(θ)和iCS(θ)的函数表达式：

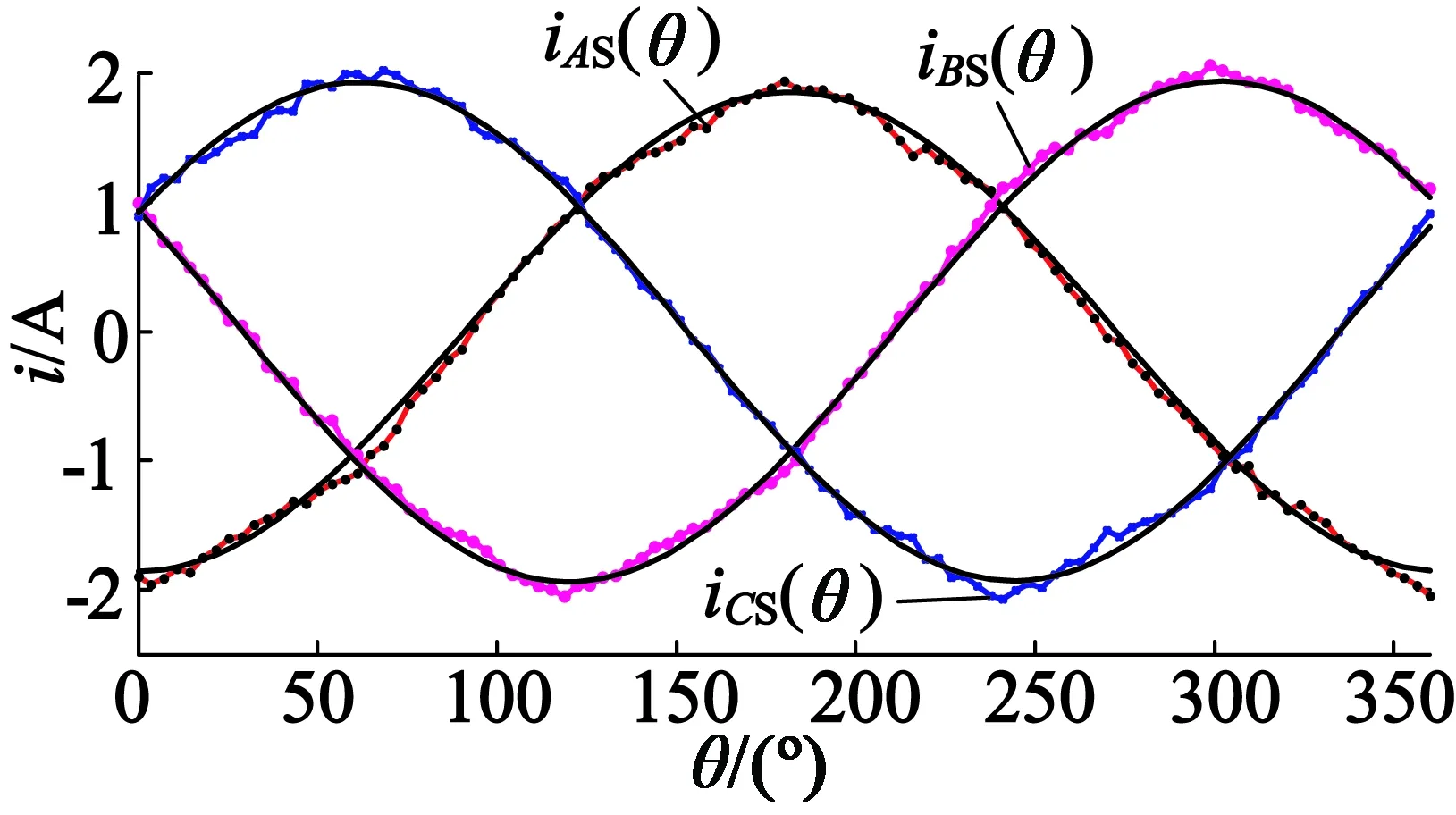
图8 iAS (θ)，iBS (θ)和iCS (θ)波形

(2)

由式(2)可以求得转子初始位置角公式：

(3)

3 实验结果分析

将原始数据累加后代入式(3)，计算获得PMSM静止状态转子初始位置角度。将检测的转子位置角、实际位置角及检测误差绘制如图9所示。

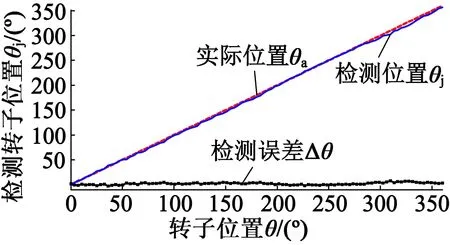
图9 检测位置与实际位置对比

由图9可知，采用本文的检测方法检测出的转子初始位置曲线与实际转子位置曲线近乎重合，实际位置与检测位置间误差在±4°范围内波动，检测精度满足绝大部分应用场合的要求。造成误差的主要原因可能有：

1)进行初始角度计算时使用的是直接采样的电流数据，其中包含有三次以上高次谐波，影响计算结果；

2)实验系统数字地与模拟地未分开，电流检测精度受实验系统影响；

3)图9在转子位置320°左右处，连续出现较大误差，因实际生产的PMSM自感和互感并不是严格随转子位置呈标准正弦变化，所以矢量激发出的电流波形与实际位置存在细微的不对应关系，致使计算出的角度存在差值，此位置误差可根据电机实际情况做角度补偿后使用。

4 结 语

本文研究了一种基于电流变化规律的PMSM初始位置检测新方法，搭建以DSP28035为核心的实验平台，通过对电机施加基本电压矢量的方式，检测电流响应并做数据分析，从电流数据中找出获取PMSM转子初始位置角的方法。通过实验测量、计算转子初始位置角误差小于±4°，验证了本方法的可靠性；同时，检测方法步骤简单、运算量小，做一次初始位置角检测时间小于10 ms，适用于具有凸极特性的PMSM，有较高的工程应用价值。