一种用于材料力学性能测试的新型原位拉伸系统

杜 扬，张 超，张 刚，叶田园，王雪薇，任万滨*

（1. 哈尔滨工业大学 电气工程及自动化学院，哈尔滨 150001；2. 北京卫星环境工程研究所，北京 100094）

0 引言

材料的力学性能表现为材料抵抗各种外加载荷的能力，由于在不同工业应用场合中材料的组分、制备工艺与结构形状各异，其力学性能有很大差异。即便是在同一工作环境下，材料的力学性能也会因为老化和其他环境影响而有所变化[1-3]。因此，准确确定和评估材料在各种工况下的力学性能，是使设备高效可靠运行需要解决的主要问题之一。

目前普遍采用的材料力学指标测试方法是拉伸测试法，是指采用液压传动或电机传动的方式，将被测材料两端与运动部件固定以对被测材料施加轴向载荷，使其产生拉伸或压缩的变形。传统方式通常在实验过程中检测材料的载荷和位移，获得其应力−应变曲线，在实验完毕后则根据试样物理参数离线计算出相关力学指标。目前较先进的方法是原位测试方式，即借助高分辨率成像设备实时检测材料在载荷作用下的微观结构变化，进而在微观尺度上研究材料力学性能与结构变化之间的关系[4-6]。然而，目前国外的大型拉伸台设备价格高昂，不具有小型、灵活的优势，很难推广应用于绝大部分普通工业产品材料的测试中。国内的拉伸台设备则普遍测量精度不高，且难以实现以极低速率施加载荷，因此在一些要求较高的精密应用场合不能满足使用要求[7-10]。

本文设计了一种用于材料测试的新型原位拉伸实验系统，具有高精度、宽量程测量应力及应变值，能实时动态检测并显示应力−应变曲线，能以极低速度对试样施加载荷的优点，且设备尺寸较小，易于应用于微型系统中，能很好满足精密测量系统的使用要求。下面介绍该系统的设计和实现方法，并采用该系统测试材料的拉伸特性曲线，定量比较线材的力学性能。实验结果可信，验证了该测试系统可以实现预期应用价值。

1 原位拉伸实验系统设计

新型原位拉伸实验系统主要由机械运动系统和测量控制系统2大部分组成。整体方案如图1所示。机械部分用于试样的安装、夹持和轴向加载；测控部分以STM32系列微控制器为核心完成载荷、位移的采集测量和电机的驱动控制，并实现采集数据与上位机间的实时通信，通过操作界面完成实验条件设定和测试波形的显示与保存等功能。本系统可在不同加载速度条件下，实时采集并自动显示材料的载荷−位移曲线，实现对材料力学性能的测试。系统可设定为多种工作模式，使被测材料分别工作在拉伸、压缩以及疲劳状态，且具有载荷和位移的双重阈值保护功能。

图1 原位拉伸实验系统整体方案Fig. 1 Schematic diagram of the in-situ tensile experimental system

1.1 机械系统设计

机械系统主要包括电机传动、试样夹具、传感器3部分，如图2所示。电机传动部分主要由电机、减速器、齿轮箱以及2对蜗轮−蜗杆组成，可将电机的旋转运动转变为蜗杆的直线运动，通过减速器可以降低蜗杆的运动速度并增大其拉力。试样两端的夹具与丝杠支座连接，且高度可调，便于夹持部件与被测材料或元件的轴线中心高度对齐。传感器部分由力传感器和编码器组成，力传感器一端与夹具相连，另一端固定在拉伸台基座上，则可测得试样轴向所受应力；编码器包括光栅尺和计数头，分别与2个丝杠支座连接固定，当丝杠支座通过丝杠−螺母实现相向运动或背向运动时，即可直接测量试验台轴向运动，以消除丝杠、齿轮的误差。拉伸台同时配有两端限位开关保护。针对不同被测材料或试样形状可配备不同的夹持组件，如各种结构的推头、拉头等，来完成材料的拉伸、压缩和疲劳试验。被测材料形变过程的实时动态观察可由实验系统配置的高倍数工业相机完成。

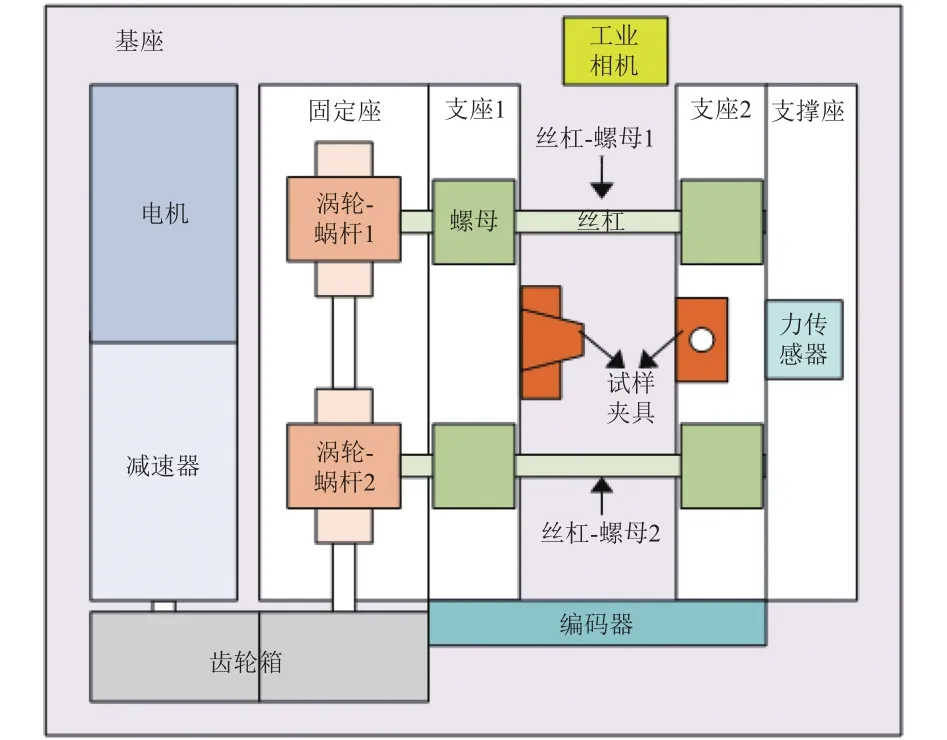
图2 原位拉伸实验系统机械结构示意Fig. 2 Mechanical structure of the in-situ tensile experimental system

机械系统的工作原理为：当电机受到激励开始旋转后，首先通过减速器降低其转速并提高其扭矩，接着通过齿轮箱内的齿轮带动对称分布的蜗轮−蜗杆，继而带动对称分布的双向丝杠旋转，在丝杠−螺母的作用下使得分别固定在丝杠支座上的试样夹具做相向或背向的直线运动，从而实现试样的压缩或者拉伸运动。在试样夹具带动试样作直线运动的同时，由试样夹具后端的力传感器采集试样的轴向受力，并由光栅尺和计数头之间的相对运动获得试样的轴向位移。

1.2 测控系统设计

1.2.1 力信号调理

原位拉伸实验系统选用的高精度力传感器测量范围4500 N。为提高力测量精度，本文提出一种分段测力方法，将力信号调理及采集电路分为3级：第1级将力传感器-48～48 mV的输出电压低噪低漂放大至-1.5～1.5 V，即电压U1，再外加 1.5 V偏置电压得到0～3 V的电压U2；第2级将U2信号送至微控制器预采样，并将0～3 V电压等分为10段，每段长0.3 V，确定U2所处的分段范围后，控制DAC通道输出该段电压的下边界值（参见图3）；第3级将U2与上述边界值间的差值U3放大并送至微控制器再次采样，依据此采样值计算应力值。其中将电压U2分成10小段后再进行放大及折算，因此理论上力的测量精度提高为原来的10倍。

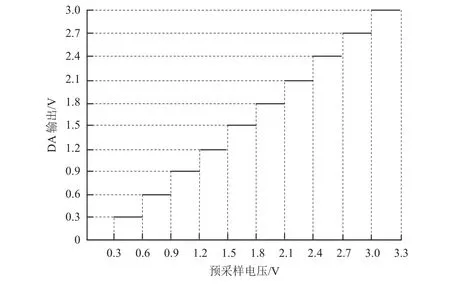
图3 微控制器DA输出电压与预采样电压关系Fig. 3 The relationship between the output voltage of the micro-controller DA and the pre-sampled voltage

测力过程中不可避免出现电压值的漂移，因此对采集电压信号应用中值滤波算法，可有效抑制信号的微小波动且延时较小，使得最终的力信号更加光滑平稳。另外测量前在力传感器不受力时，电压信号也会因漂移具有一定初始值，因此在测试过程中先减去测得的力初始值并最终计算出材料所受的真实准确应力值。应力测量算法过程如图4所示。

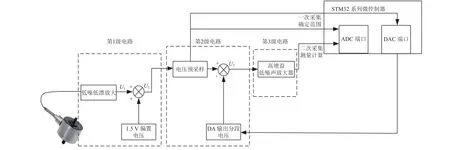
图4 力信号调理与采集过程示意Fig. 4 Schematic diagram of force signal collection and processing

1.2.2 位移信号调理

原位拉伸实验系统所采用的光栅编码器的最高分辨率为1.22 nm。微控制器自带16位正交编码计数器采集编码器输出脉冲，并根据编码器分辨率将脉冲数转换为位移值。本文利用计数器中断功能将16位计数器扩展到24位，将计数范围扩大为原来的256倍，使得系统能够以高分辨率在全行程范围内准确测量位移值。位移信号采集过程如图5所示。系统采用溢出中断延时判断算法，有效避免了高位计数器误计数情况的发生，其中延时时间根据光栅尺的分辨率和被测材料的运动速度设定。

1.2.3 电机控制系统

材料原位拉伸实验要求被测试样能以极低速度平稳拉伸/压缩，任何微小的速度波动都可能对材料力学参数的检测产生影响。为此，本文提出了一种新式的预测闭环控制算法，在1个控制周期中将直流电机的电枢方程离散化，在第k和第k+1采样时刻，其电枢方程分别为：

式中：Ce为电机反电动势常数；φ为气隙磁通；Ra为电枢电阻；U(k)、n(k)、Ia(k)分别为第k采样时刻的调速电压、计算转速和电枢电流。通过速度闭环算法最终给出本周期的调速电压U*(k)。在已知U(k)和n(k)的条件下，可以根据式(1)计算出本周期代表实际负载情况的电枢电流

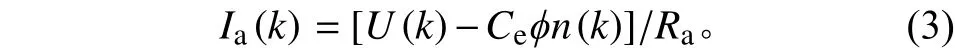
速度闭环的理想效果是：本周期输出控制电压后，在下个周期，采样速度n(k+1)等于设定速度n*，到第k+1采样时刻，调速电压等于第k个控制周期末给定的电压，即U(k+1)=U*(k)，且在一个极短的控制周期内负载变化很小，则认为Ia(k+1)≈Ia(k)，因此本周期输出的调速电压为

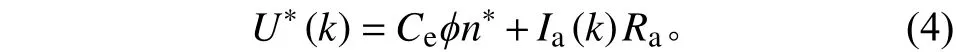
通过在每个控制周期内都进行1次调速电压反馈−预测算法，可在调速过程中不断迭代最终实现速度闭环。该控制算法的速度跟踪具有调节时间短、动态性能好的优点，其控制框图如图6所示。

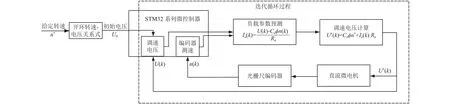
图6 速度闭环算法控制框图Fig. 6 Schematic diagram of the speed closed-loop algorithm

1.3 软件系统设计

材料原位拉伸实验系统应用LabVIEW软件设计上位机操作界面，实现与微控制器采集数据的传输通信和人机对话。操作界面具有样品参数设置，测试模式和条件设置，以及实时显示测试结果并提取特征参数的功能。其中，样品参数包括样品形状和尺寸，测试模式包括轴向拉伸、轴向压缩和轴向疲劳模式，停止条件则包括位移停止条件和负载停止条件。

拉伸或压缩实验模式下，负载停止条件规定当材料所受应力达到设置的负载阈值时制动电机，位移停止条件规定当材料应变达到设定位移阈值时制动电机。疲劳模式下，可设置每次疲劳试验的位移值及疲劳次数，达到规定次数时自动停止实验。当测试过程中出现应力过载或位移超程时，都会在操作界面中触发相应指示灯点亮并且自动制动电机，从而保证系统的安全性。

测试结束后系统可提取实验过程中被测试样的关键参数，如最大受力及其对应位移等，且所有采样点的位移和应力数据自动保存并存储在自定义的文件路径中，便于后续的文件传输和分析处理。系统软件操作界面如图7所示。

图7 微型拉伸实验台控制系统操作界面Fig. 7 The interface of the control system of the micro tensile test bed

2 测试试验及结果分析

2.1 试验条件

根据国家标准JB/T 7780[11]的规定，分别选取表面无机械损伤、裂纹、毛刺等肉眼可见缺陷的银氧化锡复合材料直线材和紫铜直线材，任意截取一定长度作为试验试样，将试样两端分别通过拉伸台的夹具进行固定。与传统拉伸台所用的试样长几十[12]甚至上百mm相比，本系统所测试的试样尺寸更小。试样尺寸以及设定的试验条件如表1所示。

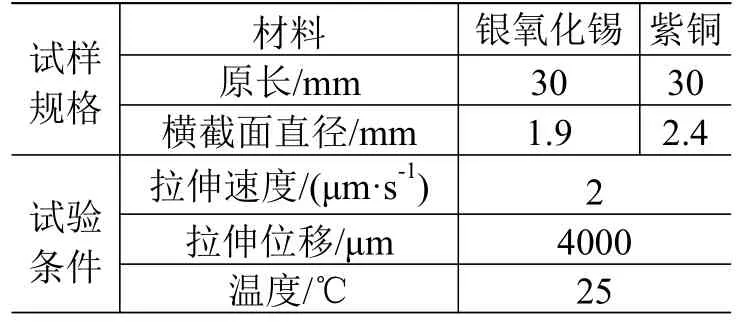
表1 试样规格参数及试验条件设置Table 1 Specifications of the experimental samples and conditions

试验过程中，实验系统在规定的拉伸速度下对试样连续均匀地施加拉力，并通过上位机界面实时检测试样的动态拉伸特性曲线，直到试样断裂，停止试验。

2.2 结果分析

绘制2组典型试样的载荷−位移特性曲线如图8所示，图中位移值采用对数坐标。完整的拉伸特性曲线包括弹性变形阶段、屈服阶段、强化阶段和颈缩阶段，直至发生断裂，不同材料的拉伸特性会有所差异。图8中银氧化锡线材和紫铜线材代表了2种具有截然不同力学性能的典型材料，两者在弹性变形阶段载荷与位移的线性度很好，紫铜材料的弹性模量大于银氧化锡材料的，表明在弹性变形阶段银锡线材具有更好的延展性。

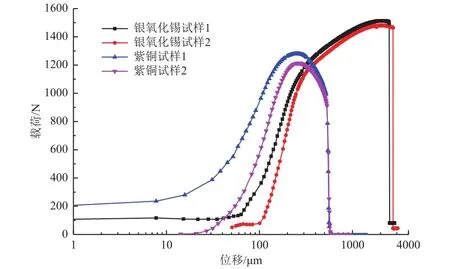
图8 银氧化锡试样和紫铜试样拉伸特性曲线Fig. 8 The tensile curves of AgSnO2 and red copper samples

根据测试数据，银氧化锡试样1在拉伸位移达到219.8 μm时进入屈服阶段，屈服力约为988.7 N；试样2在拉伸位移为246.7 μm时承受屈服力约为994.0 N，且2个试样经过屈服点后均具有很长的塑性变形及强化阶段，此阶段试样承受的载荷稳定在一较小区间内；试样1和试样2在拉伸位移为2 035.4和 2 049.7 μm 时抗拉载荷分别为 1 514.1 和1 481.1 N；最后分别在拉伸位移达到 2 509.5 和 2 733.2 μm 时发生断裂，断裂载荷分别为 1 495.9 和 1 464.5 N。

紫铜线材的屈服阶段相对较短，但具有非常明显的颈缩过程，由于形成极细的颈缩区而使得载荷迅速下降。紫铜试样1与试样2在拉伸位移为254.8和 269.7 μm 时抗拉载荷分别为 1 279.7 和 1 214.2 N；分别在拉伸位移达到521.5和532.3 μm时发生断裂，断裂载荷分别为993.7和911.1 N。

上述结果表明，银氧化锡复合线材强度大、塑性强，韧性明显优于紫铜线材。

3 结束语

本文设计了一种新型材料原位拉伸实验系统，具有微型化、高精度、多模式的特点，适用于各种形状的材料或产品的力学性能测试。系统可实时采集并显示被测材料的载荷−位移曲线，载荷测量范围4500 N、精度0.1 N，位移测量范围44 mm、精度0.1 μm，且可通过闭环控制算法将施载速度稳定控制在1～15 μm/s之间。

采用本实验系统对金属线材试样进行拉伸测试，结果表明：紫铜线材在经过较短的弹性变形阶段后迅速进入颈缩阶段而断裂；银锡线材具有较长的屈服和强化阶段，断裂时已产生较大应变，且强度和韧性均优于紫铜线材。