特长隧道洞外GPS平面控制测量数据处理模式与方法研究

毕继鑫,田林亚,李国琴,丁世一,张 洋

(1.河海大学地球科学与工程学院,南京 211100； 2.黑龙江科技大学 矿业工程学院,哈尔滨 150022； 3.苏州地质工程勘察院,江苏苏州 215129)

近些年来，中国隧道工程发展极为迅速，隧道的设计和施工水平也在不断提高和改进，越来越多的公路和铁路线路设计采用特长隧道方案。《铁路隧道设计规范》[1]和《公路隧道设计规范》[2]分别将隧道长度超过10 km与隧道长度超过3 km的隧道定义为特长隧道，我国特长隧道普遍采用GPS建立洞外控制网，许多学者、专家已从测量控制网布设[3]、控制测量方法[4]、独立坐标系建立[5]等方面对特长隧道工程的施工测量进行了研究，但不足之处在于均未对特长隧道洞外GPS平面控制测量的数据处理方法进行总结归纳，而洞外GPS控制网作为洞内控制测量和后续施工放样的起算基准，其数据处理模式与方法在确保隧道工程质量上显得至关重要。因此，本文结合在隧道工程数据处理中的实践经验，对特长隧道洞外GPS控制网的数据处理模式与方法进行研究与分析，总结归纳并形成一套适合特长隧道的洞外GPS网数据处理体系，同时得出了一些有益的结论，为隧道测量工作者对隧道洞外GPS控制网的数据处理全面了解提供参考。

1 特长隧道洞外GPS控制网基线解算软件及解算策略

1.1 几种常用基线解算软件的分析

隧道洞外GPS控制网作为洞内控制测量的起算基准，需采用高精度GNSS数据处理软件进行解算，国际主流的高精度GNSS数据处理软件有GAMIT、Bernese、PANDA和GISPY，Bernese和PANDA目前需要购买且源码不公开，GISPY因其具有较强的军方背景也不易获取，而GAMIT作为世界上最优秀的GPS后处理软件之一[6]，以其自动化程度高、运算速度快、处理精度高和源码公开等优点，被广泛用于各类工程控制网的基线解算，为便于后续施工和运营期间控制网的复测，建议隧道控制网统一使用GAMIT软件进行解算。

1.2 GAMIT数据处理软件的基线解算策略

GAMIT可以通过sestbl.、sittbl.、sites.defaults等控制文件制定不同的解算策略[7]，笔者在利用GAMIT软件进行特长隧道控制网基线向量解算相关试验后，建议采用以下解算方案能够得到精度较高的基线向量：以IGS站作为起算点，并对其X、Y、Z坐标分别设置0.03，0.03，0.05 m的约束量；统一IGS站和控制点观测数据的历元间隔为30 s，将卫星截止高度角设置为15°；基线解算模型设置为RELAX松弛解，即同时解算基线和轨道；基线解算类型设置为“1-ITER”，即对测站坐标进行一次迭代；基线观测值类型设置为适合于中长基线的LC_HELP，即使用电离层约束求解宽巷模糊度的LC解，进而抵抗电离层折射误差；干湿延迟模型均采用Saastamoinen模型，干湿映射函数均采用目前精度较高的维也纳映射函数1(VMF1)，为有效抵抗对流层折射误差对隧道控制网基线解算的影响，应采用PWL分段线性法估计天顶对流层湿延迟参数，参数的估计间隔宜设置为4～6 h；测站使用全球气压和温度模型文件gpt.grid，GAMIT可从该模型文件中内插获取测站所在地区的气压和温度。

2 特长隧道洞外GPS基线向量网平差的技术路线

2.1 三维无约束平差

基线解算完成且各项基线质量因子(RMS、RATIO、RDOP)检查合格后，进行三维无约束平差，检测隧道洞外控制网的内符合精度以及可能存在的系统误差和粗差。三维无约束平差要选择一个精度较高的IGS基准站作为起算点，且在隧道洞外控制网初次建网时采用ITRF网站[8]发布的最新ITRF参考框架及其参考历元下的IGS站坐标。作为起算点的IGS站应优先选择观测数据质量较好的参考站，根据IGS基准站稳定性分析结果[9]，中国境内的BJFS、SHAO、URUM站的观测数据质量较好，CHAN、LHAS和KUNM站的观测数据质量相对较差且时常不发布数据。

2.2 确定投影要素

隧道洞外GPS基线向量投影到二维平面实际上要经过由自然地球表面归化至参考椭球面(高程归化)，再由参考椭球面高斯投影转化至平面(投影转化)的过程，对于穿梭于高海拔山岭地区或线路横跨多个国家统一带的长大隧道工程，若使用国家坐标系会导致基线向量投影产生较大的长度变形，难以满足隧道工程后续施工放样的精度要求。《铁路工程测量规范》[10]和《公路勘测规范》[11]明确规定，当直线隧道长度大于1 000 m或曲线隧道长度大于500 m时，应根据横向贯通精度要求进行隧道平面控制测量设计。

洞外GPS基线向量由自然地球表面归化至任意参考椭球面时，要加的高程归化改正ΔS1为

(1)

式中，Hm=(HA+HB)/2，是基线所在平均高程面相对于参考椭球面的高差；H0是基线归化的任意参考椭球面相对于参考椭球面的高差；RA为基线的曲率半径；S为基线实地测量的水平距离，如图1所示。

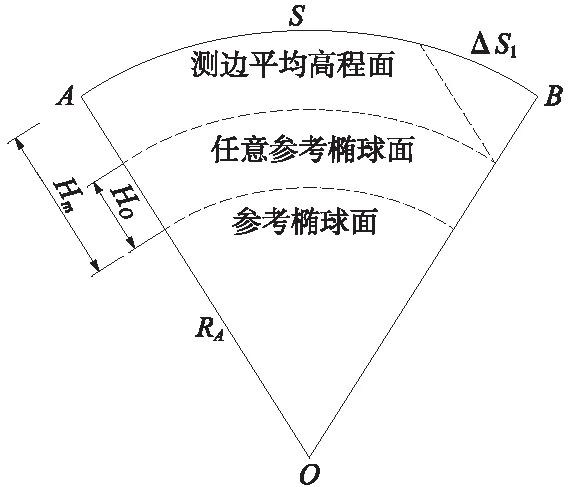
图1 实测边归化至任意参考椭球面示意

将经过高程归化后的椭球面上的长度量S0(S0=S+ΔS1)，采用高斯投影转换到平面上，要加的投影转化改正ΔS2为

(2)

式中，ym=(y1+y2)/2，是归算边两端点在高斯平面上偏离中央子午线的平均值；Rm为参考椭球面的平均曲率半径。

为控制长度变形，需采用具有高程抵偿面的任意带高斯正形投影，即通过选择合适的高程投影面H抵，并移动中央子午线Ym，以共同抵抗高程归算与高斯投影产生的长度变形，此方案往往将中央子午线移动至测区中部，边长归算到测区平均高程面上，即ΔS1=ΔS2=0。

当隧道线路为东西走向且跨度较大时，需将隧道工程分为多个投影带建立多个独立坐标系，以此解决投影变形的问题[12]。

2.3 “一点一方向”平差建立隧道独立坐标系

铁路和公路工程属于典型的狭长型线状工程，工程周围一般没有精度较高的GPS已知点，因此传统三维约束平差和工程GPS网二维约束平差并不适用，而一点一方向平差作为控制隧道轴线方向误差的平差手段，极其适用于该种控制网的平差。在进行一点一方向平差前，先将合格的基线进行三维自由网平差，再根据2.2节内容确定投影要素，最后将三维自由网平差结果投影到工程椭球对应的高斯平面上。

2.3.1 一点一方向平差函数模型

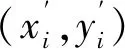
(3)

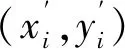
2.3.2 一点一方向平差随机模型

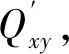
(4)

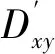
2.3.3一点一方向平差建立隧道独立坐标系注意事项

在进行一点一方向平差建立隧道独立坐标系时，固定点的坐标较容易获得，而隧道独立坐标系中固定方向的方位角一般不易直接算得，固定方向的方位角直接决定了独立控制网方向的走向，因此隧道独立坐标系中固定方向的准确计算至关重要，文献[12]提出独立网方位角的两种严密计算方法，限于篇幅，不再赘述。

隧道独立坐标系建立后，为进一步验证控制网的精度，应采用测距标称精度较高的全站仪对隧道控制网中的各条边和夹角等精度进行实测，并将实测结果与一点一方向平差坐标反算结果进行比较分析。

3 隧道洞外GPS控制网基准的统一与转换

3.1 基准统一的必要性

2018年7月1日起，国家2000大地坐标系(CGCS2000)将正式在一切测绘活动中执行，CGCS2000的使用有助于国家测绘资料基准的统一，CGCS2000是指在ITRF97框架、2000.0历元下的瞬时坐标。对于隧道洞外GPS控制网，其基准是由联测的地面基准站和所使用的卫星星历的框架及历元共同确定的，且要求联测的地面基准站的框架和历元与卫星星历的框架和历元保持一致，而IGS站提供的站坐标和速度场总是年代越晚越精确，因此在处理隧道洞外GPS网时，应采用ITRF网站[5]发布的最新ITRF参考框架及其参考历元下的IGS站坐标。综上，为统一IGS站与卫星星历的框架和历元，以及将隧道洞外GPS网纳入CGCS2000坐标系下，有必要在数据处理时进行框架转换和历元转换。

3.2 基准转换

基准转换分为先框架后历元和先历元后框架两种模式，两种模式理论上的转换结果应是一致的，本文亦采用先转历元后转框架的模式。

假设隧道洞外GPS网解算结果位于ITRFyy框架T1历元，现要将其转换到ITRFxx框架T2历元，按照先转历元后转框架的顺序，首先要将ITRFyy框架T1历元下的坐标转换到ITRFyy框架T2历元，再将ITRFyy框架T2历元的坐标转换到ITRFxx框架T2历元。

3.2.1 历元转换

将ITRFyy框架T1历元下的坐标转换到ITRFyy框架T2历元

(5)

其中

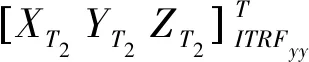
3.2.2 框架转换

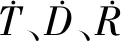
(6)

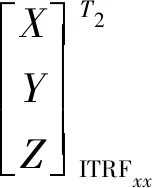
再利用布尔萨模型进行框架间的转换，计算公式为

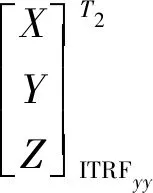
(7)

其中

4 隧道洞外GPS控制网引起的横向贯通误差严密计算

隧道横向贯通总误差主要由洞外控制测量误差和洞内控制测量误差构成，洞外GPS控制网引起的横向贯通误差可用隧道独立坐标的协因数阵进行严密计算，隧道独立坐标的协因数阵可由三维自由网平差得到的空间直角坐标的协因数阵经过三步转化得到：首先，将WGS-84空间直角坐标的协因数阵转换成大地坐标的协因数阵，然后，将大地坐标的协因数阵转换成高斯平面直角坐标的协因数阵，最后，将高斯平面直角坐标的协因数阵转换成隧道独立坐标的协因数阵。

4.1 空间直角坐标的协因数阵转换至大地坐标的协因数阵

空间直角坐标(X，Y，Z)与大地坐标(B，L，H)之间的关系为[15]

(8)

式中，N为卯酉圈曲率半径；H为大地高，对上式中的B、L、H求全微分得

(9)

对式(9)等号两边同时左乘(A′)-1，得到由空间直角坐标(X，Y，Z)转换成大地坐标(B，L，H)公式的全微分为

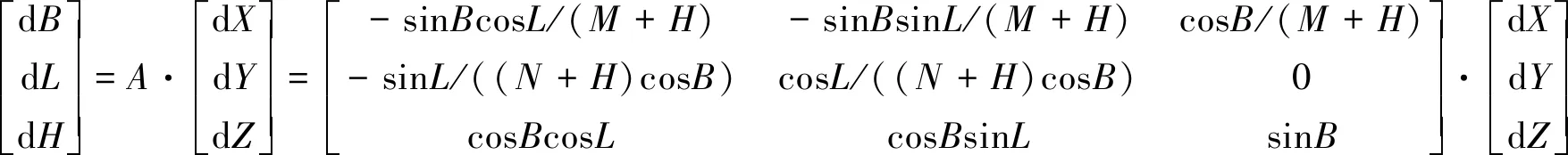
(10)

根据协因数传播定律，可知由空间直角坐标的协因数阵计算大地坐标的协因数阵的公式为

QBLH=AQXYZAT

(11)

式中，QBLH为隧道洞外GPS点大地坐标的协因数阵；QXYZ为隧道洞外GPS点空间直角坐标的协因数阵，可由三维自由网平差得到。

4.2 大地坐标的协因数阵转换至高斯平面直角坐标的协因数阵

在高斯投影坐标正算公式[15]中，略去高阶项得到大地坐标(B，L)与高斯平面直角坐标(x，y)之间的关系为

(12)

式中，l为地面点在参考椭球投影点的经度L与投影带中央子午线的精度L0之差，即l=L-L0，B、l均以弧度作为单位；X0为从赤道量至地面点在参考椭球投影点的子午线弧长，其计算公式为(e为参考椭球的第一偏心率)

(13)

对式(12)中的B、L求全微分，略去高阶项和微小项得

(14)

其中

根据协因数传播定律，可知由大地坐标的协因数阵计算高斯平面直角坐标的协因数阵的公式为

Qxy=GQBLGT

(15)

式中，Qxy为隧道洞外GPS点高斯平面直角坐标的协因数阵；QBL为隧道洞外GPS点大地坐标(B，L)的协因数阵，可从式(11)计算得大地坐标(B，L，H)协因数阵中提取。

4.3 高斯平面直角坐标的协因数阵转换至隧道工程独立坐标的协因数阵

通过地面已知点在高斯平面直角坐标系和隧道独立坐标系的双重坐标和坐标方位角，可将高斯平面直角坐标系平移旋转至隧道独立坐标系。隧道洞外GPS点在隧道独立坐标系的坐标见公式(3)，根据协因数传播率，可知由高斯平面直角坐标的协因数阵计算隧道独立坐标的协因数阵的公式为

(16)

(17)

4.4 基于坐标协因数阵的隧道洞外GPS网引起的横向贯通误差计算

如图2所示，隧道工程独立坐标系为XAY，将其按顺时针旋转φ角使坐标轴X′垂直于贯通面，形成新的坐标系X′AY′，A和B为隧道进口端控制点(A为洞口投点，B为定向点)，C和D为隧道出口端控制点(C为洞口投点，D为定向点)，E为贯通点。

图2 隧道工程独立坐标系及其与贯通面的关系

在不考虑投点误差和洞内导线测量误差时，隧道贯通的横向贯通误差由A、B、C、D四个控制点的点位误差引起，由进洞口BA、出洞口DC方向推算至贯通点E的坐标差为

(18)

式中，(XAE，YAE)为由隧道进口端推算的贯通点坐标；(XCE，YCE)为由隧道出口端推算的贯通点坐标；TAB为AB边的坐标方位角；TCD为CD边的坐标方位角，边长SEC、SEA和定向角的误差放在洞内测量中讨论，因此有微分式

(19)

其中

dTij=aij·dXi+bij·dYi-aij·dXj-bij·dYj，

aij=sinTij/Sij，bij=-cosTij/Sij

将隧道两端推算的贯通点坐标差投影到横向贯通面上，则洞外GPS控制网测量引起的横向贯通误差为

E=ΔXcos(90°+φ)+ΔYsin(90°+φ)

(20)

对式(20)取全微分

dE=-sinφ·dΔXE+cosφ·dΔYE

(21)

顾及下式

(22)

可将式(21)写成矩阵形式

(23)

其中

dET=(dXA，dYA，dXB，dYB，dXC，dYC，dXD，dYD)，

根据误差传播定律，可得由隧道洞外GPS控制网精度引起的横向贯通中误差为

(24)

5 结语

(1)解算隧道控制网基线时，基线解算策略至关重要，且不同基线解算软件采用的模型及数据处理方式互不相同，为避免产生基线解算系统误差，勘测设计、施工建设和运营管理各阶段应使用同款同版本基线解算软件。

(2)采用“一点一方向”平差建立隧道独立坐标系可有效提高隧道洞外控制网的精度，并将误差全部推到隧道出口。由于“一点一方向”平差确保了隧道横向的精度，因此隧道出口处的误差将主要体现在隧道出口控制点的纵向偏差上(里程方向)，如果隧道出口连接的是路基，则这部分误差在隧道洞外的路基上进行里程调整即可；如果隧道出口连接的是桥梁，则可考虑建立桥隧一体控制网。

(3)采用最新参考框架和参考历元下的IGS站坐标，完成隧道洞外GPS网基线解算和网平差，再结合最新速度场参数反推隧道洞外GPS网的CGCS2000坐标，此种方法可以使坐标损失精度最小。

(4)基于隧道洞外GPS网的坐标协因数阵和验后单位权中误差计算横向贯通误差公式是严密的，但仅适用于隧道洞外GPS网施测后的计算，用以衡量验后精度。