接触刚度对非连续转子整体静刚度的影响研究
□ 王 颖
上海电气集团股份有限公司 中央研究院 上海 200070
1 研究背景
非连续转子因质量轻、冷却好、易装配及各级轮盘材料选择灵活等优点,在燃气轮机和航空发动机中得到广泛的应用[1-3]。非连续转子由拉杆将轮盘、轴头等回转部件预紧成一个整体,部件间的接触效应离散了转子结构,使其不再是一个连续体,导致转子的整体静刚度相对于连续转子有一定的削弱。轮盘间接触效应对非连续转子接触段刚度存在削弱作用,使非连续转子固有频率的计算值比整体转子低,若忽略轮盘间的接触效应,则会使非连续转子固有频率的计算值偏大,甚至不可靠[4]。
当前,国内的研究人员多将非连续转子视为整体转子,或简单地以添加刚度修正因数的方法进行处理,难以满足工程上的需求[5-6]。高锐等[7]应用ANSYS软件对轮盘之间的接触机制进行研究,在一定程度上反映了轮盘之间的接触状态。李辉光等[8]借鉴机床接合面接触刚度的分析方法,采用有限元法分析了考虑粗糙表面形貌的长方微元体接触面间界面法向、切向刚度,并将其与非连续转子宏观接合面的应力状况相结合,对燃气轮机非连续转子的动态特性进行了分析。
为了建立更为精确的非连续转子有限元模型,需要对非连续转子整体静刚度与轮盘接合面接触刚度的变化关系进行研究,建立接合面动力学模型[9-10]。笔者采用均布弹簧单元模拟轮盘接合面的接触效应,建立考虑接触效应的轮盘接合面力学模型,同时考虑接触面微凸体弹塑性变形转化全过程,建立轮盘接合面接触刚度计算模型,并以某型燃气轮机非连续转子为研究对象,计算压机段轮盘接合面接触刚度,建立考虑轮盘接合面接触效应的非连续转子有限元模型,对转子临界转速进行计算,再与传统有限元模型进行对比,验证所用方法的合理性,为解决非连续转子轮盘接触问题提供了参考。
2 接合面接触效应基本理论
分形几何理论和弹塑性接触力学考虑粗糙面微凸体弹塑性变形转化的全过程,采用文献[11]中提及的微凸体接触刚度计算模型,进而推导得到非连续转子接合面法向接触刚度Knor。
单个微凸体在弹性变形阶段的接触刚度ke为:
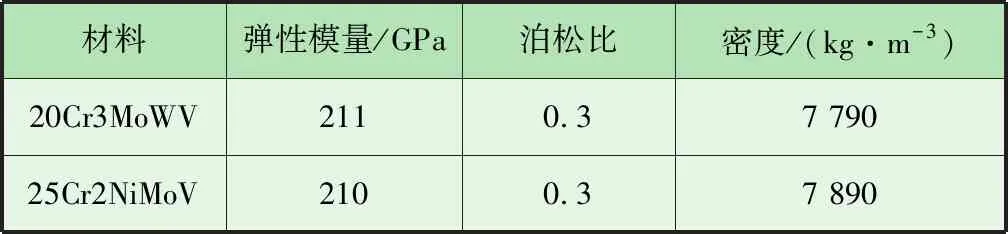
ke=2ER1/2u1/2u (1) 式中:E为接合面材料弹性模量;R为接合面表面粗糙度;u为微凸体总变形量;ue为微凸体处于弹性变形阶段的变形量[12]。 微凸体在弹塑性变形阶段的接触刚度kep为: ue≤u≤up (2) (3) (4) 式中:H为接合面材料硬度;λ接触面压因数,取0.56;up为微凸体处于塑性变形阶段的变形量[12]。 微凸体在塑性变形阶段的接触刚度kp为: kp=2πRHu>up (5) 假设一个名义面积有N个微凸体,则两个粗糙面间的法向接触刚度可表示为: (6) 式中:Φ(z)为轮盘接合面微凸体分布的概率密度函数。 获取非连续转子轮盘间的法向接触刚度Knor后,计算切向接触刚度Kτ: (7) 式中:υ为材料泊松比;A为比例因数,取0.71、2或π/2。 考虑到非连续转子轮盘接合面的结构与加工工艺等特点,笔者基于法向接触刚度来计算切向接触刚度,A取π/2。基于上述理论方法,计算获得了非连续转子在拉杆设计预紧力作用时的轮盘接合面法向接触刚度Knor为3.74×1012N/m,切向接触刚度Kτ为2.42×1012N/m。 笔者重点研究非连续转子轮盘接合面接触刚度对整体静刚度的影响规律。为了保证有限元模型的精度,划分网格时使相邻轮盘接合面上的节点一一对应,基于接合面对应的节点模化轮盘接触效应。同时,网格的均匀程度对分析精度有重要影响,因此对非连续转子三维模型进行必要的结构简化,去除结构模型中的细小特征。将模型导入Hypermesh软件进行网格划分,保证有限元网格模型单元的均匀程度。获得的非连续转子有限元网格模型如图1所示,模型共包含914 015个单元、1 120 010个节点。 图1 非连续转子有限元网格模型 在非连续转子有限元建模过程中,采用的主要单元类型及模拟对象见表1。 表1 有限元模型单元 应用Solid185单元来构造非连续转子三维固体结构,可通过八个节点来定义,每个节点有三个沿坐标轴X、Y、Z方向平动的自由度,同时具有超弹性、应力钢化、蠕变、大变形和大应变能力,适合转子模型的整体静刚度分析。 能够合理模化轮盘接合面接触效应是保证转子有限元精度的重要因素,非连续转子属于弱阻尼系统,接合面接触阻尼对转子整体静力学特性没有影响,因此在选择可模拟接触效应的单元类型时,主要考虑所选单元是否能够准确模化接合面X、Y、Z三个方向的接触刚度。ANSYS软件中的Matrix27矩阵单元可连接两个节点,每个节点有沿坐标轴X、Y、Z方向平动和绕坐标轴X、Y、Z方向转动共六个自由度,该单元中对应的实常数是一个12×12阶的矩阵,接合面法向接触刚度与切向接触刚度数值对应于矩阵元素。将接合面接触刚度按照对应关系输入Matrix27单元实常数选项,即可完成对接触效应的模化。采用上述方法建立的轮盘接合面弹簧与阻尼接触单元如图2所示。采用Contact174面与面接触单元建立燃气轮机与压机段鼓筒之间、拉杆孔与拉杆凸台之间,以及螺栓连接的绑定接触。 图2 非连续转子轮盘接合面弹簧与阻尼接触单元 准确定义模型的材料属性是有限元建模的重要过程,该非连续转子的主要结构部件包含两种材料,材料属性见表2。 表2 转子材料属性 基于应变能法对非连续转子进行整体静刚度分析,需要按照非连续转子的结构特点将其有限元模型一端固定,并在转子轮盘段的另一端添加弯矩与扭矩载荷,进而获取转子整体抗弯与抗扭的应变能。选取压机轴头靠近压机轮盘圆柱面的所有节点,约束节点的六个自由度,分别在燃气轮机轴头处添加弯矩与扭矩载荷,载荷大小为2 000 N·m。完成转子模型轮盘接合面接触效应的模化后,建立如图3所示非连续转子有限元模型。 图3 非连续转子有限元模型 以式(1)~式(7)计算获得的拉杆设计预紧力作用时轮盘接合面法向接触刚度与切向接触刚度为基准,改变非连续转子有限元模型中的接触刚度,采用应变能法对考虑轮盘接触效应的非连续转子整体静刚度进行分析,获得非连续转子有限元模型在不同接合面接触刚度时的应变能,进而研究非连续转子整体静刚度随轮盘接合面接触刚度的变化规律。在对非连续转子整体抗弯与抗扭静刚度进行计算时,非连续转子出现的弯曲与扭转变形分别如图4、图5所示。 图4 非连续转子弯曲变形 图5 非连续转子扭转变形 经计算分析,获得了36组不同接触刚度时的非连续转子有限元模型整体静刚度,见表3。 基于表3数据,同时考虑轮盘法向接触刚度与切向接触刚度之间的函数关系,笔者给出非连续转子整体抗弯与抗扭刚度随法向接触刚度的变化规律曲线,分别如图6、图7所示。图6、图7中合并体模型表示将转子所有零部件合并成一个实体,类似于结构连续的实体轴转子。由于轮盘接合面接触效应的存在,非连续转子的整体静刚度只可能无限接近于合并体模型。 由表3与图6、图7可以看出,当法向接触刚度与切向接触刚度分别小于1.74×108N/m、1.12×108N/m时,改变轮盘接合面间的接触刚度,对非连续转子的整体抗弯与抗扭刚度影响较小,这是因为轮盘接合面间的接触刚度较小时,燃气轮机与压机轮盘间的刚度主要由对应的拉杆提供,而轮盘间的接触效应对非连续转子整体刚度无明显影响。当法向接触刚度处于1.74×108~3.74×1012N/m之间、切向接触刚度处于1.12×108~2.42×1012N/m之间逐渐变大时,非连续转子的整体静刚度随轮盘接合面间接触刚度呈线性提高趋势,轮盘接合面接触效应对非连续转子整体静刚度影响明显。当法向接触刚度与切向接触刚度分别大于7.74×1012N/m、1.12×1012N/m时,非连续转子接触体模型的整体静刚度与合并体模型无限接近,并且随着接合面接触刚度的增大,非连续转子整体静刚度几乎不再变化。在拉杆最小设计预紧力工况下,非连续转子接触体模型的整体抗弯、抗扭刚度与合并体模型的分别相差1.88%、1.56%,表明非连续转子具有较好的连续性。 图6 非连续转子整体抗弯刚度随接触刚度变化曲线 图7 非连续转子整体抗扭刚度随接触刚度变化曲线 笔者以某型燃气轮机非连续转子为研究对象,建立考虑轮盘接合面接触效应的非连续转子有限元模型,以计算获得的拉杆设计预紧力作用时的轮盘接合面法向接触刚度与切向接触刚度为基准,改变非连续转子有限元模型中的接触刚度,研究非连续转子整体静刚度随轮盘接合面接触刚度的变化规律。在非连续转子的设计过程中,可以以笔者提出的研究非连续转子整体静刚度随接合面接触刚度变化规律的方法,确定拉杆的预紧力,进而保证非连续转子的连续性。 表3 非连续转子整体静刚度3 非连续转子有限元建模
3.1 有限元网格模型

3.2 单元类型选择
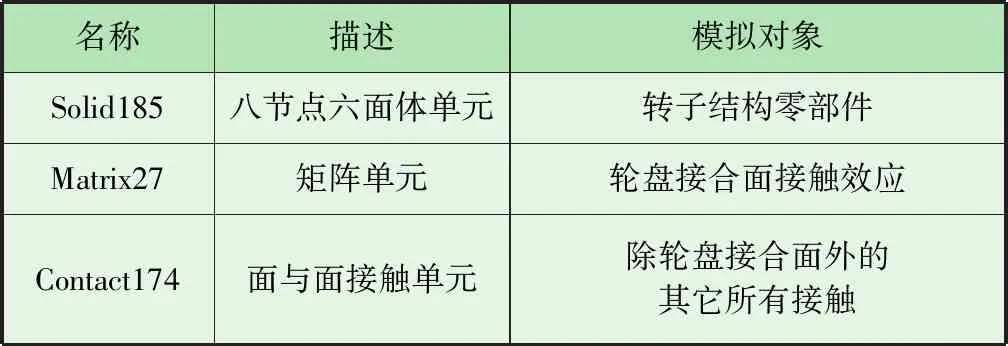
3.3 接触效应模化

3.4 材料属性定义
3.5 载荷添加

4 非连续转子整体静刚度分析




5 结束语


