基于某推力机构弹道修正弹角运动稳定性分析*
邢炳楠,张志安,高光发,雷晓云,盛娟红
(南京理工大学机械工程学院智能弹药技术国防重点学科实验室,南京 210094)
0 引言
对现代战争而言,弹药精确打击的重要性在战场上体现的越发明显。弹道修正弹作为新兴制导武器中的一种,在提高打击精度,减小打击误差上以及低成本等方面具有非常突出的优势。如何保证在修正力作用下弹丸依然具有良好的飞行稳定性是非常重要的问题。而弹箭飞行过程中攻角变化可以直观地反映出其稳定性变化。
目前二维修正弹药多采用鸭舵或者脉冲发动机方式进行修正,在文献[1]中,王中原等人以旋转弹为研究对象,从理论上简单分析了在修正力系下的弹丸角运动方程,并在此基础上讨论了其对飞行稳定性影响变化。但缺少一定的数值仿真论证。Murphy在对自旋导弹稳定性研究的过程中,通过建立弹箭的角运动方程,推导出关于弹箭的自由飞行稳定性判据,但是对于其中非线性因素的考虑有一定的局限性[2]。杨红伟等在文献[3]中通过建立脉冲修正弹角运动方程组,对弹道修正过程中弹丸转速过程中弹丸转速的变化进行分析,并得出结论:脉冲作用的径向偏心是造成弹丸转速大幅变化的主要原因。大家认识到转速变化对弹箭稳定性影响有非常重要的作用。Daniel Corriveau[4]主要在建立线性攻角运动模型基础上,讨论在双脉冲矢量条件下如何将角运动稳定性尽可能提高,对于研究修正机构依次先后作用下的攻角变化具有非常重要的意义。在文献[5]中,姚文进提出了在确定适当的转速条件下,将对提高弹丸修正能力非常有利,并通过设置不同脉冲参数对修正效果进行了分析。但并没有通过建立攻角运动方程进一步分析扰动对弹箭稳定性影响。曹小兵等人通过建立攻角方程讨论了强扰动下的攻角运动响应特性,并通过控制脉冲冲量及其距弹体质心距离为变量,探讨一个基于最大允许攻角的变量约束条件[6]。
本文对采用新型“预置质量块”修正的低旋尾翼弹进行研究,并用Matlab软件进行六自由度弹道建模分析,认为修正力对弹箭造成冲击扰动,基于这一基础上建立复攻角运动方程。由于转速对弹箭修正能力有很大影响,以及低旋尾翼弹会容易发生共振闭锁现象,运用变系数方法考虑转速变化对弹箭攻角运动变化进行分析。为了保证修正弹的飞行稳定性,主要对扰动下弹丸的动态稳定性以及追随稳定性进行分析,探讨弹箭受到强扰动时影响稳定性的重要因素,以期对设计具有良好气动布局的弹丸提供参考意见。
1 某新型推力修正弹动力学建模
1.1 某新型推力机构基本修正原理
目前国内外现有的主要二维修正方法为鸭舵修正和脉冲发动机修正。本文中所讨论观点均基于一种新型“预置质量块”式推力修正机构。该修正机构主要作用原理为:通过在某低旋尾翼弹质心之后围绕弹体呈环状多层布置多个质量块,利用射出质量块造成的推力对弹箭飞行过程中进行横向和纵向的二维修正,从而提高落点精度和打击效率。具体修正机构示意图如图1所示。

图1 预置质量块式新型修正机构剖面示意图
根据修正机构原理分析,选取相关坐标系,设单个质量块造成推力大小为FP,预置质量块与弹轴坐标系Oη轴之间夹角为γP。

图2 修正力作用示意图

设预置质量块所在横剖面距质心距离为lP,则可得预置质量块对质心的作用力矩MP投影至弹轴坐标系为:

1.2 修正弹丸六自由度弹道模型
根据以上推导可得无控6D弹道方程中由于外力矢量变化而变化的质心运动方程中的3项为:

由于外部力矩变化而变化的弹丸绕心运动方程为:
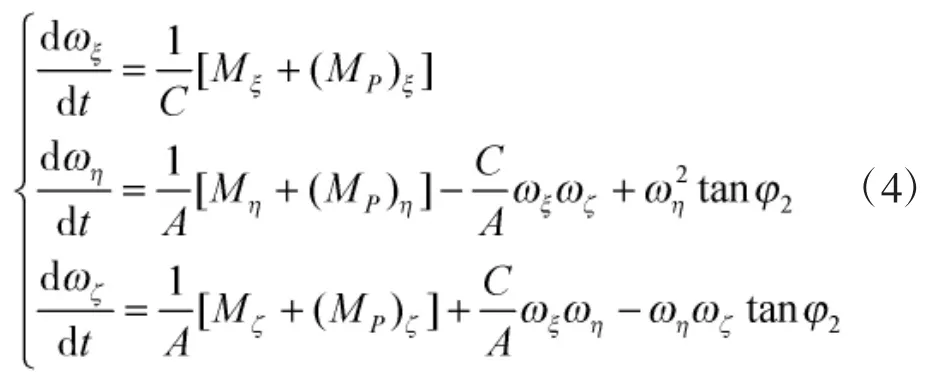
将式(3)、式(4)分别代入无控飞行标准六自由度弹道方程组中,其余方程组不变即可得到修正力系作用下弹丸的六自由度弹道方程。
2 修正力系下角运动分析
2.1 修正力系下攻角运动方程
建立角运动方程时的一些假设前提如下:在小攻角线性化假设前提下定义复攻角为(δ1,δ2为高低攻角与方向攻角),。其中称为复摆动角(φ1,φ2分别为高低摆动角和侧向摆动角),用来确定弹轴空间方位,将称为复偏角,用于确定速度线方位(分别为高低偏角与侧向偏角);并且可以近似认为都是小量,有关系式成立(上述符号含义均参见文献[7])。
由式(3)、式(4)可知,修正力对复偏角引起变化,修正力矩使复摆动角发生变化。并有以下关系式成立:
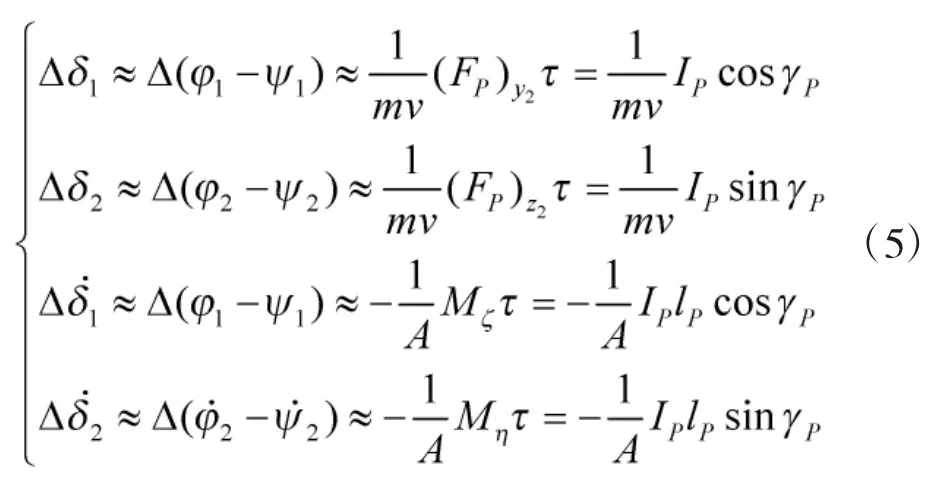
在认为预置质量块造成的推力使低旋尾翼弹受到冲击扰动前提下,根据文献[1]所得,考虑风W作用下,认为攻角运动方程如下所示:

其中,B为常数,表示周期干扰的幅值,γ为预置质量块作用角度与弹轴坐标系Oη轴之间夹角:

但考虑到马氏力本身很小,由横风产生的附加马氏力更小,所以方程中bz值很小,一般只有10-5量级,故可以忽略该项影响。并着重考虑弹丸受到冲击扰动情况下角运动稳定性分析,为了消去和Δ前的因子v2和v,将自变量从时间t改为弧长s,经过推导得简化后修正力作用下攻角运动方程如下:

2.2 冲击扰动下的角运动解析解
欲对冲击扰动作用下弹箭角运动进行准确分析,需求得式(8)分析求解。易知式(8)为非齐次方程,根据微分方程理论可知,其齐次方程的解表示了在起始扰动条件下的角运动,可考虑将作用前攻角条件认为是起始扰动条件,对式(8)进行求解。
设方程齐次方程解析解形式如下[6]:
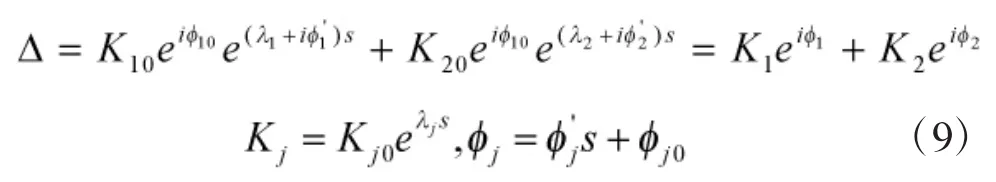
由文献[7]可知角运动对于攻角初始扰动有以下关系式成立:


设推力作用前攻角为Δ1,作用后为Δ2。由关系式(5)可知,有:
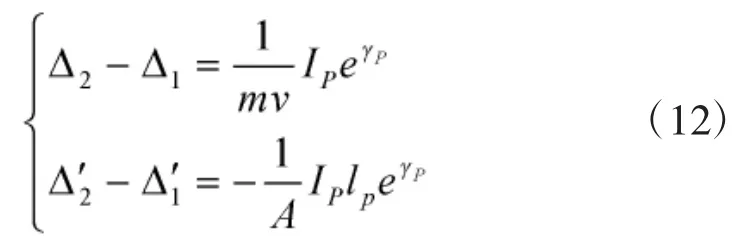
则将式(10)~式(12)代入式(9)即得式(8)解析解表达式。
一般情况下,采用常系数法对式(9)进行分析,但实际弹箭角运动方程中系数会随空气密度变化,为了更精确地分析弹箭角运动变化,可以采取平均法对角运动变化进行分析。
设变系数情况下攻角方程解仍为二圆运动形式,即式(9)。与常系数冻结法不同的是,此处对作为弧长s的一般函数处理。

在变系数情况下频率方程保持不变,阻尼方程如下:

P'由于系数可变产生,由于转速对修正弹的修正效果有很大影响,进一步讨论在仅有转速项P变化情况下,得到阻尼系数如下:

易知马赫数以及空气密度变化会引起M变化。在仅考虑空气密度变化对角运动方程系数变化影响情况下,可以得到阻尼系数表达式如下[7]:

则将式(15)、式(16)代入式(9)可讨论缓变系数项条件下攻角运动变化。
3 角运动稳定性及仿真结果分析
对于低旋尾翼弹而言,由于低速旋转,因而其陀螺效应很弱,甚至可以忽略不计,所以广义上认为静稳定尾翼弹具有陀螺稳定性。而为了保证弹箭飞行稳定性,要求弹丸绕弹道切线有迅速衰减的摆动,没有共振效应,并且在弹道曲线段应具有追随稳定性,同时更重要的是应满足动态稳定性[8]。
3.1 推力修正下弹箭追随稳定性分析
弹箭的追随稳定性主要根据动力平衡角的变化进行分析,动力平衡角是由于弹道弯曲引起的。弹箭可能在重力法向分量mg sinθ作用下攻角不断增大并最终发生弹底着地情况,而过大的动力平衡角会破坏弹箭的飞行特性,造成其散布增大,并且一定程度上造成射程减少[9]。因此,研究弹箭飞行的追随稳定性具有非常重要的意义。
仅考虑重力作用下的尾翼弹角运动方程为:

考虑到研究对象为低旋尾翼弹,由于赤道阻尼力矩项H较大不能忽略,略去其马格努斯力矩项PT及较小量级项后,设有动力平衡角,则有:

且由式(8)处分析可知,修正阶段与无控飞行阶段角运动方程相比,仅方程中马氏力矩项T上有所区别,但是由于研究对象为低旋尾翼弹,推导过程中T忽略不计。所以可以认为修正力系下弹箭追随稳定性与无控飞行时保持一致[10-11]。
为得到满足追随稳定性条件,根据理论分析结果,运用Matlab软件,下面对低旋尾翼弹在铅直面内动力平衡角δ1p与侧向动力平衡角进行全弹道仿真分析,仿真结果如图3所示。

图3 动力平衡角变化曲线
3.2 修正力系下弹箭动态稳定性分析
根据参考文献[7],对于无控飞行弹箭动态稳定性而言,其稳定的根本条件是,即要求弹箭在运动中攻角不断衰减,则此处对修正力系作用下弹箭动态稳定性条件进行探讨。考虑到式(15)、式(16)由于变系数引起附加阻尼项,则采用Matlab软件进行6D推力修正弹道仿真,分别得到常系数条件下和考虑P',M'3种情况下阻尼系数变化。选取弹道上出炮口位置、弹箭上升下降阶段中1/2弹道射高处,以及弹道最高点,着地之前5个不同部分阻尼项参数如表1所示。

表1 阻尼系数项比较
根据表1中数据分析可得对于低旋尾翼弹而言,相对于M'项,转速项P的变化对阻尼系数影响更大,一定程度上可以近似认为常系数和考虑M'情况下阻尼方程一致。故在分析动态稳定性问题时,选取考虑转速项P变化条件下的阻尼方程准确性更高。
由于弹箭动态稳定性主要通过攻角变化趋势进行反映。根据推力作用下攻角运动方程式(8),选取表1中第2组参数中考虑转速项下阻尼指数,通过Matlab仿真图直观表明修正力系下攻角运动变化响应。
除阻尼指数外,选取其余参数项数据如下:

图4 复攻角运动曲线

图5 高低攻角δ1变化曲线

图6 方向攻角δ2变化曲线
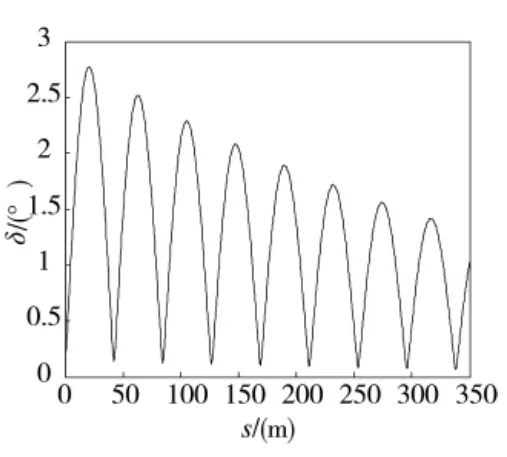
图7 复攻角幅值变化曲线
4 结论
通过理论分析与仿真计算,对于“预置质量块式”修正弹在修正力系下的弹丸角运动稳定性可得出以下结论:由于马氏力矩比较小,则动力平衡角解中T项忽略不计,静力矩起更为重要的作用。认为动力平衡角变化与未施加修正力时基本一致,修正弹满足时弹箭具有追随稳定性。且对于修正弹,在考虑角运动响应时选取考虑转速项P变化条件下的阻尼系数,其准确性更高。且在满足条件下,修正弹箭动态稳定得以保证。

