考虑天然裂缝成簇分布的压裂液滤失研究

游先勇，赵金洲，李勇明，许文俊

（西南石油大学油气藏地质及开发工程国家重点实验室，四川成都610500）

由于裂缝净压力会导致压裂液向储层中滤失，这对储层压裂后水力裂缝的尺寸、支撑剂分布以及地层污染情况都有着较大的影响。对于天然裂缝发育的储层，压裂液会优先选择渗透率更大的天然裂缝作为渗流通道，从而加剧滤失速度和增大滤失量。

Stahl和Clark对比分析了不同类型储层压裂液的滤失规律，发现天然裂缝是压裂液滤失的重要原因，并且相交天然裂缝是压裂液渗流的重要通道[1]。Barree和Mukherjee在研究压裂液滤失时，考虑裂缝内压力变化，分析了裂缝扩展延伸行为对压裂液滤失的影响[2]。Nagel等建立了考虑天然裂缝的诱导应力场分布模型，并利用该模型对压裂液滤失过程中裂缝内压力变化进行了分析[3]。夏富国等考虑天然裂缝的动态滤失，根据压力连续及流体体积守恒原理，建立了针对天然裂缝储层的压裂液滤失模型，并分析了天然裂缝性质、施工参数等对压裂液滤失的影响[4]。李勇明等利用有限元方法建立了考虑储层裂缝网络的压裂液滤失模型，并求得了其数值解。该方法模拟了不同形态裂缝网络对压裂液滤失过程中储层应力分布的影响[5]。郭建春等建立了张开天然裂缝滤失介质形成力学判别模型，发现在裂缝性储层中张开裂缝是压裂液滤失的主要原因，并分析了净压力、泊松比等参数对裂缝张开和诱导应力的影响[6]。赵立强等通过建立离散裂缝网络，利用等效渗透率张量原理将其转化为各向异性连续介质，通过建立二维压裂液滤失模型来分析天然裂缝分布对压裂液滤失速度和滤失量的影响[7]。

目前国内外学者研究天然裂缝对压裂液滤失的影响时，仅仅将天然裂缝作简化处理，并未考虑其成簇分布的特点，因此该方面研究仍存在局限性。通过分形离散裂缝法生成分形离散裂缝网络模型，刻画了天然裂缝成簇分布的特点，并将其等效为渗透率张量，最后建立了基于等效渗透率张量的压裂液滤失模型，分析了成簇分布的天然裂缝对压裂液滤失的影响。

1 分形离散裂缝网络模型

通常情况下，裂缝会以簇的形式分布于储层中[8]，传统的离散裂缝网络（DFN）的建立，主要是通过泊松分布对裂缝中心进行刻画描述[9]（图1a），但是这种方法生成的天然裂缝分布较为均匀，无法体现天然裂缝成簇分布的特点，即天然裂缝成团成簇地在储层中分布；而分形离散裂缝法（FDFN）是基于离散裂缝网络法，通过采用倍增串级的方法来生成天然裂缝网络（图1b），从而更真实地刻画出地层中裂缝的分布特征[10,11]。

分形离散裂缝法的核心思想是：尽管储层中发育的天然裂缝分布错综复杂，但不同大小区域的分形维数却趋于常数，根据这个特征便可以较合理地刻画成簇分布的天然裂缝[12]。

FDFN的核心算法公式为：

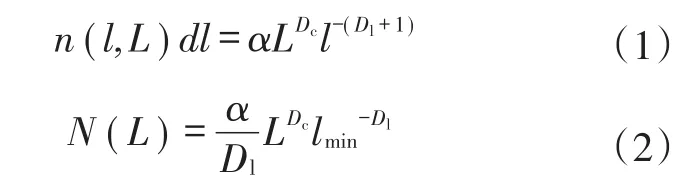
式中：n（l，L）dl为在L尺寸储层区域内长度在l与dl之间发育裂缝总数量，条；Dc为裂缝分布的分形维数，无因次，表征裂缝的聚集程度，取值范围一般为[1.5，2]；Dl为裂缝长度的分形维数，无因次，表征裂缝长度的分布规律，取值范围为[0，∞]，其值越小，长裂缝的出现概率越大；α为裂缝发育密度，无因次，与选取储层区域大小无关；L为研究区域尺寸，m；l为裂缝长度，m；lmin为天然裂缝尺寸下限，m；N（L）为长于lmin的天然裂缝数量（较小尺寸裂缝将被忽视），条。

1.1 裂缝分布分形维数

裂缝分布的分形维数采用径向分布函数来进行计算：

图1 两种模式下的裂缝中心分布Fig.1 Fracture center distribution generated by two methods

式中：C2（r）为裂缝分布的径向分布函数；Np（r）为r距离内的粒子数（裂缝数），个；N为裂缝总数，条；c为拟合出的常数，无因次。通过此公式来计算裂缝分布的分形维数Dc。

1.2 生成满足条件的裂缝分布

该模型采用倍增串级方法来生成满足条件的裂缝网络，该方法不仅能生成符合分形维数的天然裂缝中心位置，且能体现其成簇发育的特点。这是一种迭代方法，其思想是将储层区域不断剖分成小的子区域，将每个区域生成裂缝的概率也随之剖分，从而使概率大的地方裂缝发育，概率小的地方裂缝稀疏，直到满足条件为止。倍增串级的算法公式为：

式中：Pi为概率；sr为剖分比例；Dc为裂缝分布分形维数，无因次；q为常数，二维情况下取2。

1.3 裂缝走向

天然裂缝的走向可以采用Fish分布来进行表征：

式中：θ为裂缝偏离平均走向的角度，（°）；K为Fisher常数，无因次，一般通过露头数据得出，表示与平均值的偏差程度（K越大，裂缝走向一致性越强）。

为了产生裂缝方向，裂缝角度偏差，裂缝偏离角RFK可以根据式（6）计算得出。

式中：RFK为裂缝偏离角，（°）；RG为高斯随机数，无因次，取值介于0～1；K为Fisher常数，无因次。

1.4 建立分形离散裂缝网络模型

通过输入裂缝网络的几何参数，包括目标区块裂缝分布分形维数Dc、裂缝尺寸分形维数Dl，裂缝密度系数α，裂缝最短长度lmin，裂缝发育带平均走向及Fisher常数K，利用Matlab编写分形离散裂缝网络的数值化模型，建立目标区块的天然裂缝网络。

2 等效渗透率张量

2.1 渗透率张量计算方法

渗透率张量是岩石渗透率具有方向性的体现。低阶张量在各领域运用广泛，标量是零阶张量（只有一个值），向量是一阶张量（一个值和一个方向），而岩石的渗透率张量是二阶张量（一个值和两个方向）。张量可以理解为同时改变向量大小和方向的矩阵，且不随位置的改变而改变。

二维情况下岩石的渗透率张量可以表示为：

Lamb等人在研究裂缝孔隙双重介质中流体流动时提出，在利用有限元对双重介质进行网格剖分时，网格块可以看作是两个区域的叠加（图2）[13]。

图2 离散裂缝区域中基质和裂缝单元的表征Fig.2 Schematic representation of the matrix and fracture elements from discretized fractured domain

此时，裂缝渗透率张量可以用式（8）进行表征：

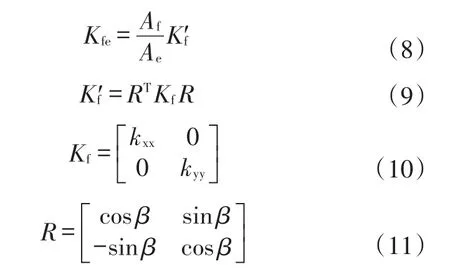
式中：kxx=kf；kyy=km；Kfe为裂缝单元的渗透率；Af为单元内的裂缝面积，m2；Ae表示单元面积，m2；K'f为局部笛卡尔坐标下的裂缝渗透率张量；Kf为裂缝方向上的渗透率张量；kxx为裂缝渗透率张量在x方向的主值，10-3μm2；kyy为裂缝渗透率张量在y方向的主值，10-3μm2；kf为天然裂缝渗透率，10-3μm2；km为基质渗透率，10-3μm2；β为天然裂缝与水平方向的夹角，（°）。

利用上述公式可以将离散裂缝网络图通过叠加原理生成等效渗透率张量。

2.2 有效表征体积计算方法

等效连续介质模型是连续介质模型和离散裂缝网络模型的结合体，是研究裂缝性储层渗流规律的有效方法。但将裂缝性介质转化为等效连续介质必须满足研究域内存在表征体积单元（REV）这个条件。卢波等人认为REV尺度应该大于节理迹长的三倍[14]，而朱冬林，庞作会通过实验研究，得出裂缝性岩石的REV尺度应该达到典型节理迹长的四倍到八倍的结论[15,16]。对于节理迹长在3 m以下的裂缝性储层，该模型符合等效条件。

3 滤失模型建立及求解

根据渗流力学理论，流体在地层中的渗流连续性方程为：

式中：ρ为压裂液密度，g/cm3；φ为岩石孔隙度，%。

若考虑储层岩石和压裂液流体的压缩性，将其状态方程代入式（12），则等式右边可以表示为：

式中：P0为原始地层压力，MPa；φ0、ρ0分别为P0压力下的地层孔隙度、压裂液密度，g/cm3；Cφ、Cρ分别为岩石孔隙度、压裂液的压缩系数，MPa-1。

将全渗透率张量及式（13）代入式（12）可得：

初始条件：

边界条件：

①封闭外边界条件：

②封闭内边界条件为：

③已知压力的内边界（水力裂缝）：

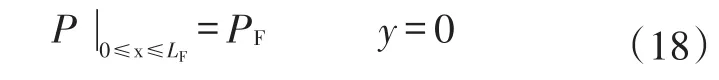
式中：P0为原始地层压力，MPa；PF为裂缝内压力，MPa；Lx为x方向研究区域长度，m；Ly为y方向研究区域长度，m。

对式（14）进行差分离散，利用Matlab进行快速求解。

4 实例分析

在400 m×400 m的区域中，利用储层裂缝网络参数（表1）生成分形离散裂缝网络，然后将其等效为渗透率张量，代入到压裂液滤失模型中，结合地层的基本参数（表2），对压裂液的滤失过程进行模拟和分析。裂缝分布分形维数Dc和裂缝尺寸分形维数Dl分别在其取值范围内取2和3，然后随机生成满足分形维数的离散裂缝网络。

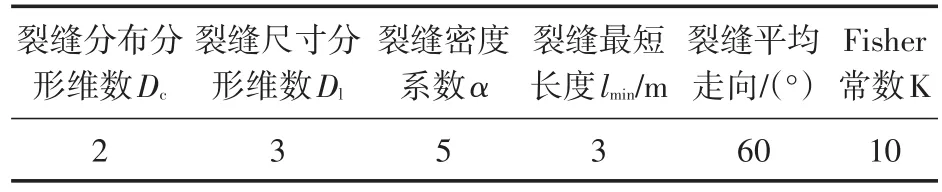
表1 储层裂缝网络参数Table1 Parameters of reservoir fracture networks

表2 地层基础参数Table2 Basic parameters of formation

图3表示利用分形离散裂缝法生成的400 m×400 m的分形离散裂缝网络。该方法共生成了406条天然裂缝，裂缝长短不一，分布杂乱，且具有成簇分布特征。利用第二节中所述方法将其转化为等效渗透率张量，代入滤失模型。

图3 400 m×400 m的分形离散裂缝网络Fig.3 Fractal discrete fracture networks with a dimension of 400 m×400 m

图4和图5表示压裂液滤失到地层中20 min和80 min后地层孔隙压力分布。结合图3可以看出，由于天然裂缝的随机分布，压裂液滤失过程中压力波也存在非均匀传播的特征。但是从图5不难看出，由于天然裂缝发育带走向呈现北偏东的趋势，因此压力波也率先传播到地层的东北方，从这个特征也可以看出，天然裂缝发育带的走向在宏观上对压裂液的滤失方向和压力波的传播方向起着决定性的作用。

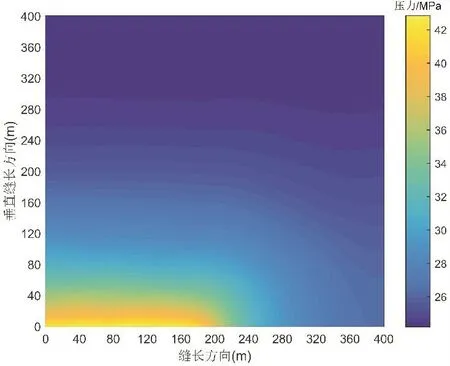
图4 地层孔隙压力分布（20 min）Fig.4 Distribution of formation pressure（20 min）

图5 地层孔隙压力分布（80 min）Fig.5 Distribution of formation pressure（80 min）

图6说明垂直于裂缝壁面上压裂液的滤失速度随净压力的变化而变化。随着净压力的增大，裂缝壁面处的滤失速度也越来越快。结合图3可以看出，在靠近壁面40 m左右的地方，有一条接近10 m的长裂缝，从而造成在裂缝壁面40 m处，滤失速度较其他地方明显较大，这说明压裂液是优先从天然裂缝中进行滤失，且在局部位置，长裂缝对压裂液的滤失有着关键的控制作用。

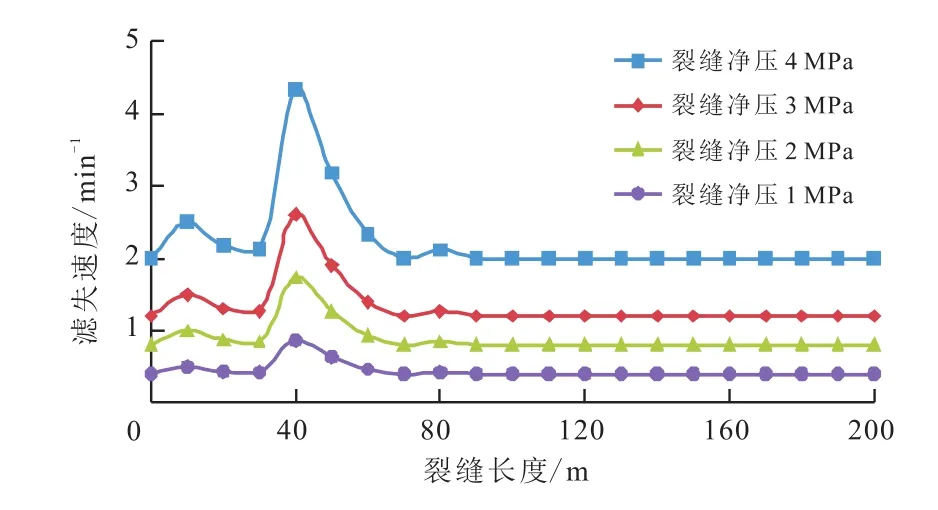
图6 垂直裂缝方向不同净压力下压裂液的滤失速度Fig.6 Filtration rate under different fracture net pressure at the direction perpendicular to hydraulic fracture

图7表示在裂缝壁面50 m处不同压裂液黏度（10 mPa·s、15 mPa·s、20 mPa·s、25 mPa·s）下压裂液的滤失速度，刚开始滤失时，由于裂缝内压力与壁面处的孔隙压力之间压差较大，所以滤失速度也较快。当壁面处的孔隙压力增大时，滤失速度也迅速减小。从图7可以看出，随着压裂液黏度的增大，压裂液的滤失速度在初期减小的幅度较大，随后幅度逐渐降低。

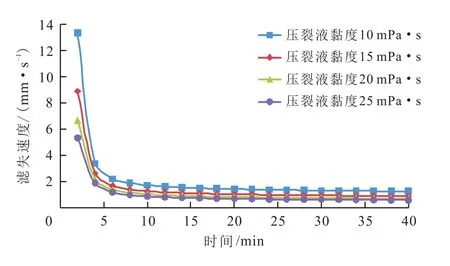
图7 不同压裂液黏度下压裂液的滤失速度Fig.7 Filtration rate of different fracturing fluid viscosity

5 结论

1）基于分形离散裂缝法，建立了储层二维分形离散裂缝网络，合理地表征了裂缝储层中天然裂缝成簇分布的特点，更加符合实际。

2）利用已建立的离散裂缝网络模型，通过单元剖分，将其转化为渗透率张量，有利于在数值模拟过程中研究天然裂缝的随机非均匀分布特征对压裂液滤失行为的影响。

3）建立了基于渗透率张量的压裂液滤失模型，研究了天然裂缝成簇分布特征对压裂液滤失的影响。计算结果表明，压裂液优先从天然裂缝中进行滤失，且天然裂缝发育带的走向在宏观上决定了压裂液的滤失方向和压力波的传播方向；压裂液会沿着长裂缝进行滤失，建议压裂施工前对裂缝壁面处的天然裂缝进行封堵；压裂液黏度对滤失速度也有一定的影响。