高密度客流激波现象识别与分析

孙立山，宫庆胜，崔 丽，赵鹏飞，乔 婧

(北京工业大学 城市交通学院，北京 100124)

0 引 言

由于准点率高、安全性好、快速便捷等优势，轨道交通已经逐渐成为我国大中城市居民出行的主要交通方式。高密度的客流压力下，轨道交通客流管控压力和安全风险隐患日渐严重，其中尤以设施瓶颈处最为突出。如何快速准确地实现设施瓶颈处由于客流压缩形成的激波传递现象的识别，是客流组织管控和风险预警的重点和难点。

在交通流激波现象的识别方面，M. J. LIGHTHILL等[1]首次采用一阶连续介质模型识别了道路交通激波的存在，并分析其特性及应用，成为激波理论研究的基础；张心哲等[2]提出基于Hough变换方法和模糊C均值聚类方法的交通状态辨别方法，实现了对拥堵波动状态的识别。在激波现象的分析方面，邓文等[3]运用交通流的动态演化机理，分析了由下游瓶颈造成的拥堵向后传播的规律以及瓶颈能力恢复后拥堵消散的规律；贾丽斯[4]运用R/S分析法与去趋势涨落分析法分析了交通瓶颈处各相态密度时间序列以及交通时间序列的相关特性，得到标度关系与幂率关系；A. SEYFRIED等[5]则在研究行人轨迹的基础上，引入泰森多边形模型来研究瓶颈之前的行人密度随时间波动变化关系，为行人设施的设计提供了理论依据。在激波现象的模拟验证方面，冯士德等[6]根据微观和宏观之间的质量、动量、能量守恒准则，利用格子Boltzmann模型模拟激波现象，从理论和试验两方面验证了格子Boltzmann模型的适用性；孙明玲等[7]采用交通流波动理论，模拟事件解除前和解除后车流集结排队和消散过程的变化，并利用VISSIM仿真验证其有效性；针对部分道路关闭导致的激波现象，孙晓燕等[8]采用平均场理论分析和确定性NS元胞自动机规则分别对建立的交通流模型进行解析和数值模拟验证，得到了系统存在3种稳定的物理状态。

综合而言，在激波现象的识别、分析以及模拟验证方面，已有的研究主要针对道路交通中车辆产生的激波现象进行，对行人流激波现象的研究较少，已有的激波波速计算方法复杂且不够精确。本研究利用行人可控试验模拟轨道交通通道瓶颈，标定获取行人微观特性参数，并引入DTW算法实现对行人流激波现象的识别、分析与论证。

图1 激波现象可视化流程Fig. 1 The visualization flow chart of shockwave phenomenon

1 DTW算法

DTW算法由日本学者板仓最早提出，因其在匹配并获取两个时间序列的最佳对应关系上的精准性优势，随后被广泛地应用于语音识别、模式识别、故障诊断等领域[9-11]。J. TAYLOR等[12]将DTW算法引入到车辆跟驰模型中，从微观层面描述了车辆运行的异质性。基于车辆与行人跟驰特性的制约性、延迟性和传递性的相似性[13]，利用DTW算法对行人流激波现象展开研究。

1.1 时间序列距离度量方法

距离度量可用于确定时间序列之间的相似性，欧式距离与DTW距离是两种典型的距离度量方式。欧氏距离d是指两个时间序列中两个离散点(a1,b1)，(a2,b2)间的距离，要求各时间序列长度是相同的，其计算公式为

(1)

DTW距离则是通过时间轴获取两个时间序列各个时间点的最小距离，确定各点的最佳对应关系。与欧式距离相比，DTW距离更能描述两个时间序列的相似性，有效地弥补了欧式距离中难以解决的时间长度不等的不足，较好地解决了欧氏距离难以处理的对应数据间沿时间轴方向的伸缩、弯曲等问题，如图2。

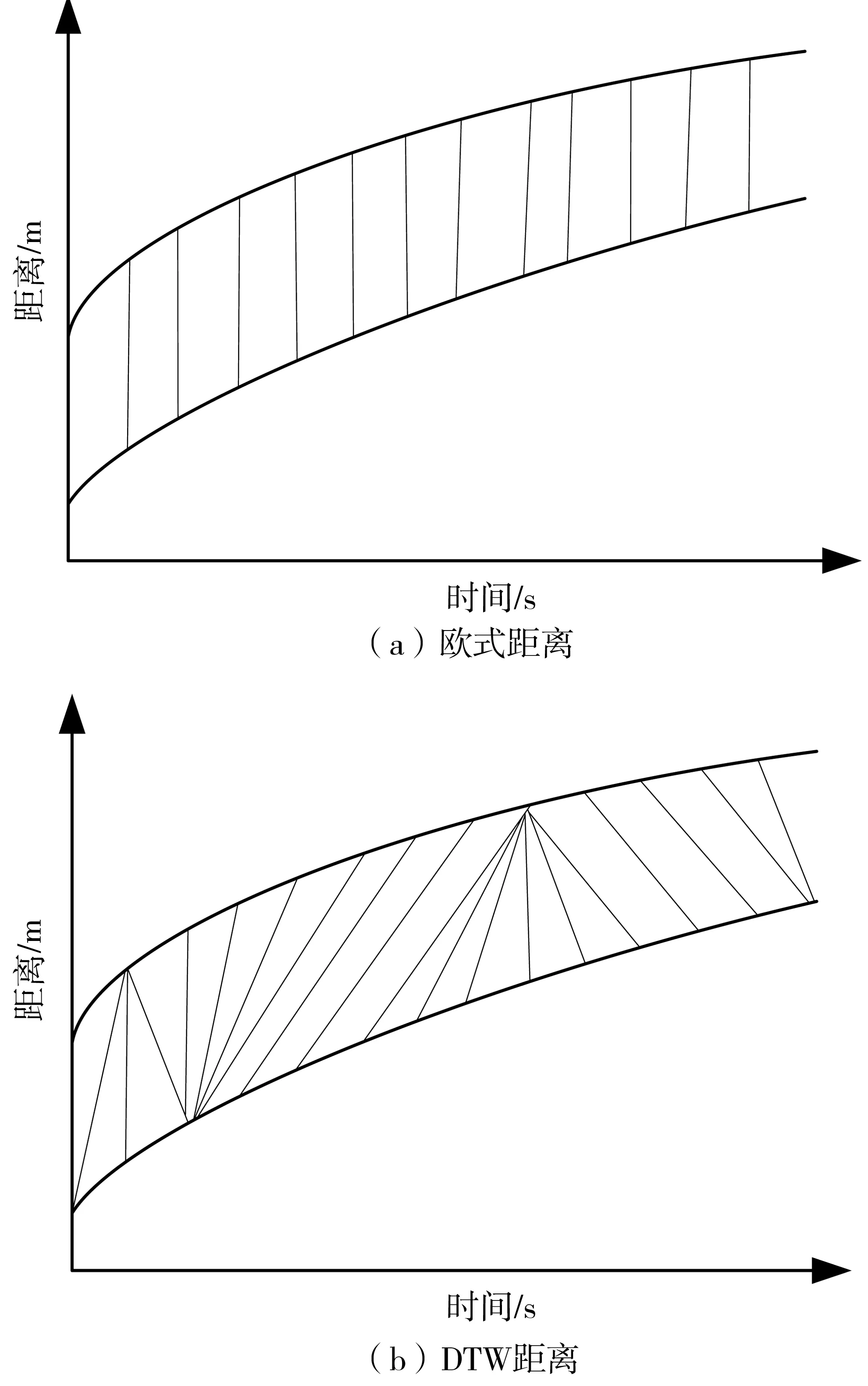
图2 欧式距离与DTW距离的比较示意Fig. 2 Comparison of example Euclidean distance and DTW distance

1.2 DTW算法步骤

为了更好地运用DTW算法研究行人激波现象，以两个行人的微观特性参数为例，具体的计算步骤如下：

1)标定获取两个行人的位移与速度时间序列，见表1。

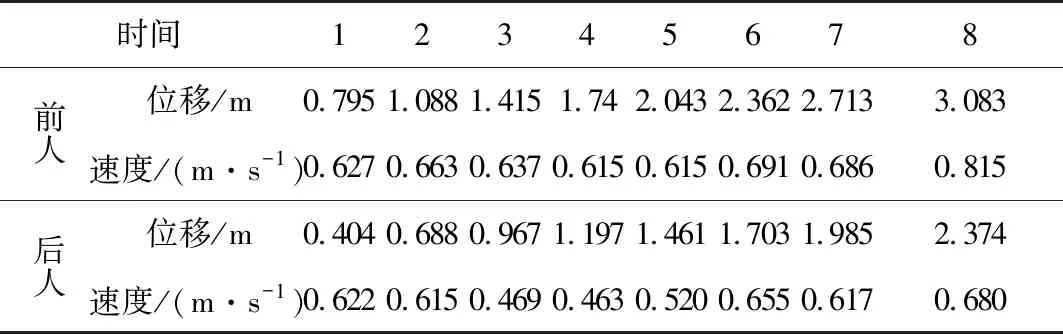
表1 位移与速度时间序列数据 Table 1 Displacement and velocity time-series data

2)利用公式(2)构建基于速度时间序列差的初始化相似矩阵C：

(2)

式中:cij为第i时间点与第j时间点的速度差值，m/s；ai为前人速度特征矢量序列，m/s；bj为后人速度特征矢量序列，m/s。

得初始化相似矩阵C，如下：

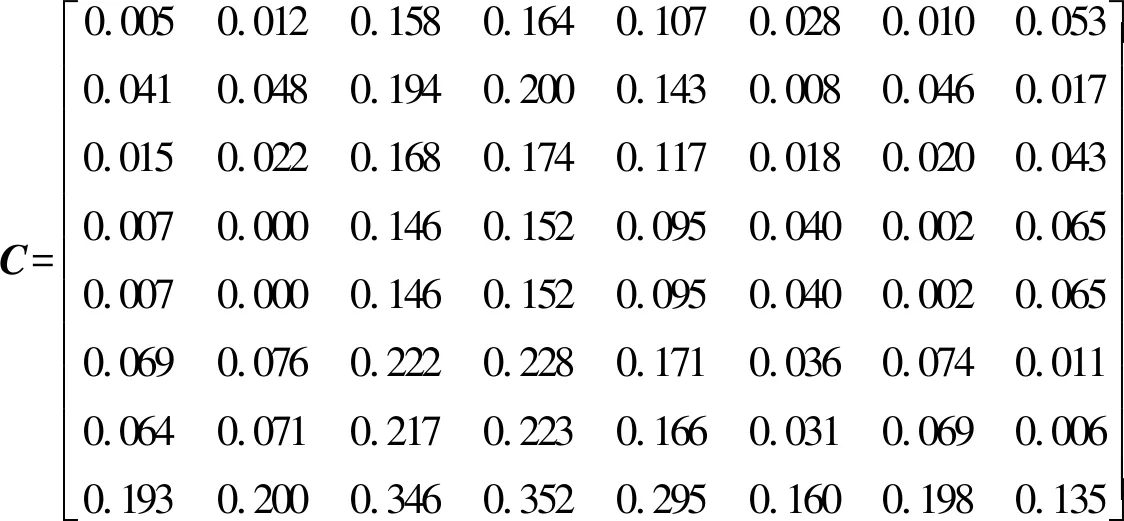
3)运用公式(3)的递推关系，基于初始化相似矩阵C得到累积相似矩阵L。

(3)

式中:lij为第i时间点与第j时间点累积速度差值，m/s。

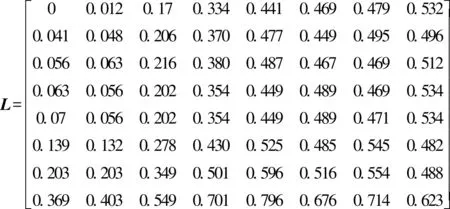
4)回溯获得全部匹配点对，找出最优路径。寻找最佳路径时，由最后一个匹配点对向前回溯到起点的最短路线，即为最优路径。所得最优路径如下(下划线部分)。

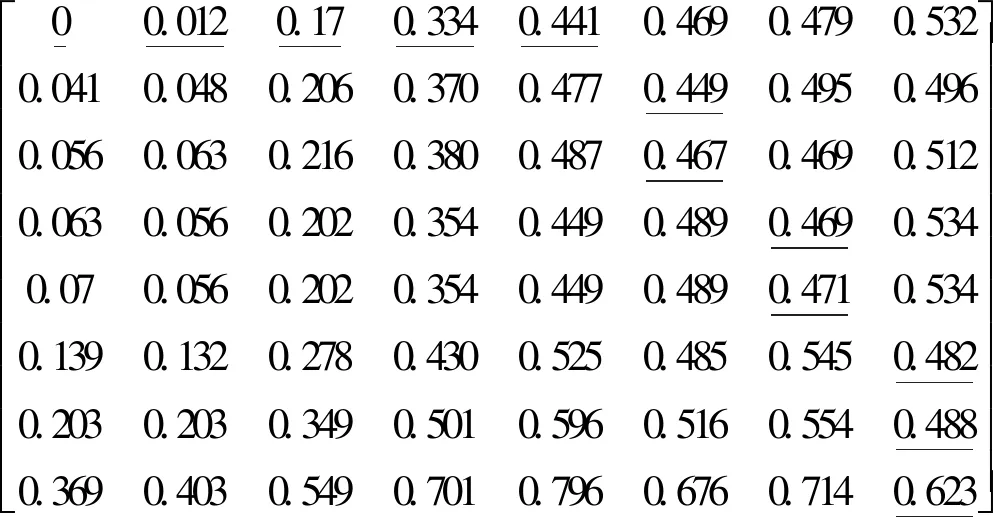
5)图像匹配。绘制行人时间-位置匹配波动图像，得到速度、位置等时间轴向量间的最佳对应关系，分析行人流状态转化，找到状态的波动传递现象。将最优匹配时产生的交点定义为奇点，夹角θ为奇角(图3)，这是由于DTW算法中允许一个时间序列点与多个时间序列点进行最优匹配产生的。另外，最优路径的形成是由最后一个时间坐标向前寻优的过程(即从右下角向左上角寻优)，在此过程中可能出现水平、竖直以及对角线方向数值相同的问题，为减少匹配点的数量，以对角线方向为最优。

图3 DTW算法匹配轨迹结果Fig. 3 Results of DTW algorithm matching trajectory

2 行人可控试验

受到枢纽内部空间高度的限制，实际通道瓶颈处的视频数据获取范围难以满足行人微观特性提取要求。为此，采用行人可控试验开展通道瓶颈模拟并扑捉激波现象，如图4。试验场景瓶颈宽度为1 m(北京地铁中常见瓶颈宽度，如扶梯)，正常的通道宽度为4 m，两侧挡板高2 m；试验人员身高为(170±10)cm，互不相识；为便于标定，试验过程中试验员佩戴蓝色帽子，由正常通道向瓶颈通道方向行走；利用SIMI Motion软件，获取行人的时间、位移、速度等微观行为参数。

图4 行人可控试验场景Fig. 4 The scene of the pedestrian controlled experiment

3 激波现象的识别、分析与论证

3.1 激波现象的识别

选取连续通过瓶颈单列9位行人微观行为数据，运用DTW算法，结合MATLAB编程，获得最佳匹配曲线。由图5、图6可以看出，行人在进入瓶颈的过程中产生奇角数量较多，客流波动现象明显，速度下降较快，此时客流状态极不稳定；在进入通道后，匹配曲线趋于平缓，奇角数量减少，客流波动现象微弱，速度变化趋于平缓，客流趋于稳定状态。同时，在最优曲线匹配过程中，发现客流激波的传递现象，如图5线圈所围区域。

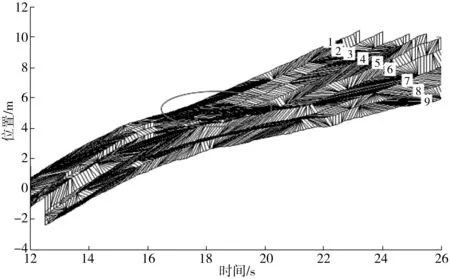
图5 最优匹配结果Fig. 5 The optimal matching results

3.2 激波现象的分析

可控试验中，由于通道宽度由4 m减少到1 m，断面的通行能力降低，行人发生拥挤，导致行走速度降低，形成集结波并向后传递；通过瓶颈后，通行能力得到恢复，客流逐渐开始消散，密度降低，直至恢复正常通行状态。

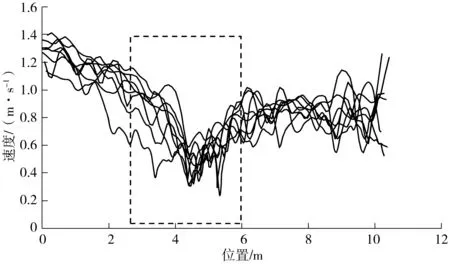
图6 行人速度位置分布Fig. 6 The distribution of pedestrian speed and position

3.2.1 波 速

由图5可见，客流波动最终传递到了第6人。对前6人的波动传递现象作进一步分析，如图7，由于第1人和第2人间的最优匹配无明显规律，表明传递现象是从第2人开始的。由匹配图像可以看出，线AB、CD、EF、GH表示波速沿此分界客流向后传播，为低密度状态向高密度状态转化的分界，表征客流的集结波；线IB、JE、EF、LH表示波速沿此分界客流向前传播，代表客流的疏散过程，即由高密度状态向低密度状态转化的分界，表征客流的消散波；各线的斜率即为波速。点A、C、E、G、I、J、K、L均为变速点。

提取图7中关键点的坐标、波速以及相邻奇点构成的三角形面积，其中三角形面积大小与激波的影响程度相关，面积越大则影响越严重，反之，则影响越小，如表2。

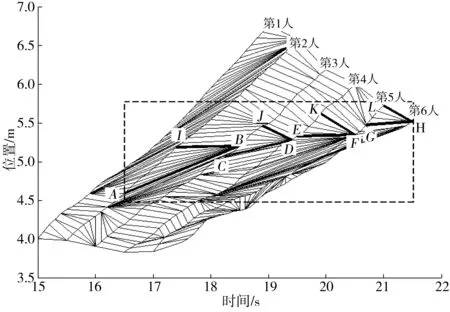
图7 匹配结果波动传递现象Fig. 7 Wave transfer phenomenon of matching results

关键点时间/s位置/m 波速k/(m·s-1)三角形面积S/m2A16.54.588B18.55.203C18.25.064D19.45.278E19.55.284F20.55.342G20.75.473H21.45.470I17.55.240J18.95.462K19.95.618L21.05.727kAB=+0.308kIB=- 0.037kCD=+0.178kJD=-0.368kEF=+0.058kKF=-0.46kGH=+0.053kLH=-0.643S△ABI=0.34S△CDJ=0.16S△EFK=0.15S△GHL=0.07

由表2可知，kAB>kCD>kEF>kGH，表明客流集结波的波速是逐渐向后传播且逐渐减少的；|kIB|><|kJD|><|kKF|><|kLH|>，表明客流消散波的波速是逐渐向前传播且逐渐增加的；另外，面积S△ABI>S△CDJ>S△EFK>S△GHL,表明客流波动影响程度随波速传递逐渐递减。

3.2.2 密 度

密度也可以描述客流波动状态变化。客流在瓶颈前时，行人间距较大，密度较低，客流状态稳定；当经过瓶颈处时，行人间间距变小，密度显著增大，行人拥挤状况严重，客流状态不稳定；当经过瓶颈后时，行人间距开始变大，密度逐渐减低，客流状态趋于稳定。客流在瓶颈处的密度呈现出“低密度→高密度→低密度”的状态转化，见表3。

表3 区域密度分布值 Table 3 Distribution values of regional density

3.3 激波现象的验证

运用流体动力学理论算法，对6人的波动传递现象作进一步分析,提取行人试验中连续通过瓶颈的单列行人的轨迹，如图8，各曲线间的水平距离表示行人时距，垂直距离表示行人间距，行人轨迹可分为Ⅰ、Ⅱ、Ⅲ3个时空区域，在Ⅰ区域内，行人速度高而密度低，客流状态较稳定；进入Ⅱ区域后，行人速度明显降低而密度升高，客流状态不稳定；进入Ⅲ区域后，行人速度逐渐升高而密度逐渐降低，客流状态逐渐趋于稳定。

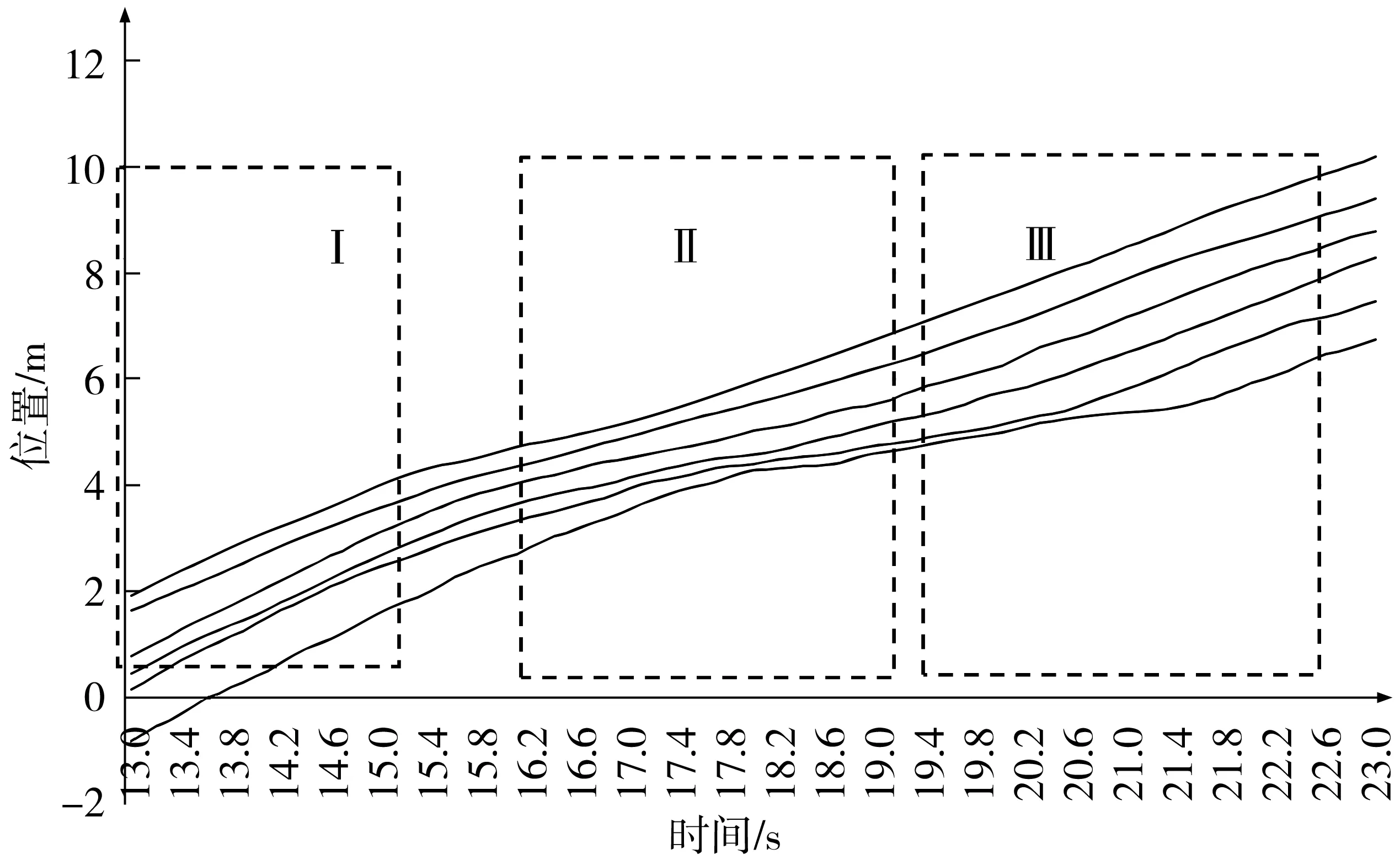
图8 单列行人流轨迹Fig. 8 Trajectory of the single-lane pedestrian flow

波速的计算公式为

(4)

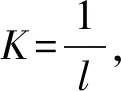
所以，波速的计算公式为

(5)

式中：W为波速，m/s；Q1,Q2为不同状态下的流量，人/(s·m)；K1,K2为不同状态下的密度，人/m2；v1,v2为不同状态下的速度，m/s；l1,l2为不同状态下的行人间距，m。

由行人试验数据，统计代入公式(5)得行人流波速变化如表4:

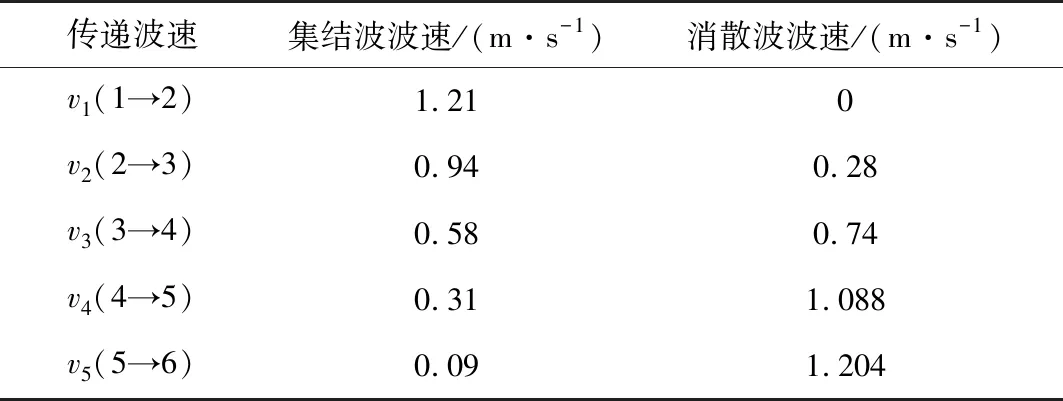
表4 行人流波速变化值 Table 4 Wave velocity variation of pedestrian flow

由图9可知，运用流体动力学理论算法与DTW算法获得的集结波与消散波波速变化趋势是一致的，证明了DTW算法研究客流瓶颈处微观波动现象是有效的。与流体动力学理论算法相比，DTW算法具有以下两方面优势：

1)在状态变速点识别方面， DTW算法可以获得变速点的准确位置坐标，且可准确找到激波传递的起点，比流体动力学理论算法通过区域均值计算寻找更加直观、精确。

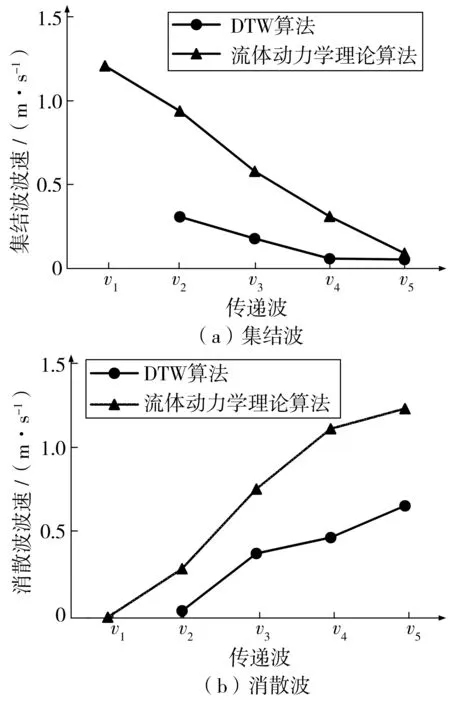
图9 波速传递变化对比Fig. 9 Contrast chart of variation of wave velocity transmission

2)在激波波速计算方面，DTW算法提供了一种利用位置坐标计算波速的方法，与流体动力学理论算法相比，计算复杂度显著降低。

4 结 论

通过行人可控试验的方式，在获取行人微观行为参数的基础上，运用DTW算法对通道瓶颈处客流激波现象进行识别与机理分析，描述了瓶颈处行人的微观波动现象，主要结论包括：

1)证明了DTW算法研究客流激波现象是有效的，其结果能够刻画行人微观波动规律；

2)DTW算法提供了一种新的计算波速的方法，与流体动力学理论算法相比，提高了计算的精度，降低计算的复杂度；

3)运用DTW算法发现了客流在瓶颈处聚集产生的激波传递现象；行人在瓶颈前集结过程中，集结波传递时波速逐渐降低；在消散过程中，消散波传递时波速逐渐增大；行人的集结与消散过程中，激波的影响程度逐渐降低。