周期平均控制下固定翼双旋弹角运动特性分析

张鑫，姚晓先，杨忠，郭致远

1. 北京理工大学 宇航学院，北京 100081 2. 鲁东大学 交通学院，烟台 264025

现代战争要求武器的打击精度高，附带损伤小；同时为了降低成本，有效利用库存，常规弹药简易制导化技术得到了发展。其中，常见的一种方法是将常规引信替换为修正引信[1-2]。鸭式布局双旋弹[3]作为修正弹药的一种，其修正引信和弹体由轴承连接，分别绕弹体纵轴低速和高速旋转，这样既可以为引信的正常工作提供条件，又可以保持弹丸的陀螺稳定性。

目前，国内外对鸭式布局双旋弹的研究较多。Costello和Peterson[4]发展了双旋弹的线性化理论，并利用该理论研究了双旋弹的稳定问题。法德联合Saint-Louis研究所(ISL)对双旋弹进行了一系列系统性研究[5-11]。Chang等[12]研究了鸭式布局双旋弹前后体的旋转特性以及其间的耦合关系。许诺等[13-14]推导了固定翼双旋弹的动力学模型，分析了其角运动特性和飞行稳定性；对固定翼双旋弹的非线性动力学进行了分岔特性分析，并研究了各系统参数对其动力学分岔特性的影响。常思江等[15]研究了鸭式布局双旋弹的前体鸭舵周期性干扰引起的强迫运动。张冬旭[16]研究了一种固定翼双旋修正机构的方案和系统设计，采用基准脉冲和反馈脉冲的形式来解算控制偏差。

对于固定翼双旋修正组件，传统的控制方法不能获得幅值可调的控制力。文献[17-18]提出了2种基于周期平均思想的控制力连续可调控制方法，但是并没有分析在周期平均控制下弹体的角运动响应。在此基础上，本文基于固定翼双旋弹的动力学模型，分析了周期平均控制下固定翼双旋弹的角运动响应，进而根据双旋弹的角运动特性和执行机构的性能给出了周期平均控制角频率的选择范围，并仿真验证了上述分析。

1 角运动模型

与常规鸭式布局双旋弹相比，固定翼双旋弹由于采用了固定角度舵片，其成本更低、结构更简单。如图1所示，双旋弹可分为前体和后体两部分，后体为与弹体固连的部分，前体为带有固定舵片的低速旋转鸭舵部分。舵片1和舵片3组成一对差动舵，用于为前体提供减旋力矩；舵片2和舵片4组成一对控制舵，用于产生作用于弹体的控制力。当不需要弹道修正时，前体在差动舵的作用下低速反向自由旋转，对弹道的平均修正作用近似为零；当需要进行弹道修正时，前体中的轴向电机按照修正指令控制前体的滚转角度。

图1 固定翼双旋弹执行机构示意图Fig.1 Schematic diagram of actuator of dual-spin projectile with fixed-canards

忽略舵面控制力的效果，只考虑控制力矩的影响，则得到固定翼双旋弹角运动方程为

Δ″+(H-iP)Δ′-(M+iPT)Δ=

(1)

Δ=Δ1+Δp+ΔF

(2)

式中：Δ1为式(1)对应的齐次方程的通解；Δp为由重力引起的动力平衡角；ΔF为舵控制作用引起的角运动的强迫响应。

齐次方程的通解Δ1可写为

Δ1=C1e(λ1+iω1)s+C2e(λ2+iω2)s

(3)

式中：系数C1和C2由初始条件决定；λ1和λ2为阻尼指数；ω1和ω2为角运动频率，可表示为[6]

(4)

(5)

双旋弹属于静不稳定弹，有kz>0，也即M>0。同时双旋弹的陀螺稳定性也保证了P2>4M[6]。综上易得，ω1,2>0且ω1>ω2，因此也将ω1称为快圆运动频率，将ω2称为慢圆运动频率。

由重力引起的动力平衡角Δp可表示为

(6)

对于舵控制引起的角运动的强迫响应，当采用周期平均控制时，前体滚转角周期性变化，因此可采用傅里叶变换，将带前体滚转角的项eiγw写为

(7)

(8)

式中：k为整数；T0为在自变量为弧长s时周期平均控制的周期，即前体滚转角变化的周期；ω0为弧长s域中周期平均控制的角频率，并且有ω0=2π/T0。

由于双旋弹为旋转稳定弹，因此有λ1,2<0，于是ikω0≠λ1,2+iω1,2。根据常系数线性微分方程理论，对于式(7)中的某一项ckeikω0s，其引起的角运动强迫响应，也就是式(1)的一个特解可写作

ΔF,k=CF,keikω0s

(9)

将式(9)代入式(1)，令重力相关项为零，则可得到

CF,k=

(10)

则周期平均控制下角运动强迫响应ΔF为

(11)

综合式(3)、式(6)和式(11)，则固定翼双旋弹在周期平均控制下的角运动方程的解析解可由式(2) 给出。

2 角运动分析

对于固定翼双旋弹在周期平均控制下的角运动方程的解析解(式(2))，由于双旋弹的旋转稳定性，阻尼指数λ1和λ2均小于0，因此齐次方程通解Δ1的幅值会逐渐衰减为0，衰减的速度与阻尼指数的大小有关；由重力引起的动力平衡角Δp只与重力有关；下面将重点分析周期平均控制下角运动的强迫响应ΔF。

由式(11)，对于周期平均控制下角运动强迫响应ΔF，将其中k=0的项单独提出，记为ΔF,0。实际上，ΔF,0即为周期平均控制下，对应傅里叶变换式(7)和式(8)中常数分量c0的动力平衡角。ΔF中k≠0的项对应的是角频率为kω0的圆运动，记作ΔF,k。ΔF,0为周期平均控制期望得到的动力平衡角，也就是周期平均控制下得到的理想控制效果，而各项ΔF,k对应的圆运动为不希望的扰动，可能会对弹体的飞行产生不利的影响，因此希望ΔF,k的幅值相对ΔF,0越小越好。

常数分量c0对应的动力平衡角ΔF,0可表示为

(12)

当前体滚转角固定时，也即γw为常数时，由前体控制产生的动力平衡角Δc可由式(1)求得

(13)

对比式(12)和式(13)，可定义c0的幅值|c0|为周期平均控制的效率，定义c0的相角∠c0为等效前体滚转角，则周期平均控制产生的动力平衡角等效于前体的同向舵舵偏角为|c0|δw，滚转角为γw=∠c0时产生的动力平衡角。于是通过调节周期平均控制的状态，来改变c0的幅值|c0|和相角∠c0，就可以得到等效的任意方向的连续控制力的控制效果，这也是周期平均控制的原理。

对于ΔF中k≠0的项，将式(10)代入式(11)，并将式(10)的分母写成实部和虚部分离的形式，得到

(14)

由式(14)可见，|ΔF,k|一方面受周期平均控制状态的影响，即受ck和ω0影响；另一方面受弹本身的参数和飞行状态的影响。由于ck与具体的周期平均控制选择策略有关，而ω0、弹本身的参数和飞行状态对|ΔF,k|的影响对所有周期平均控制具有普遍性，因此去掉式(10)中的ck，令CF,k,p为

(15)

则ΔF,k可化为

ΔF,k=CF,k,pckeikω0s

(16)

于是通过研究ω0、弹本身的参数和飞行状态对|CF,k,p|的影响，得到普遍意义下的周期平均控制中|ΔF,k|的变化规律。

观察式(15)可得，当

kω0=ω1,2

(17)

时，CF,k,p的分母的实部为0，会造成|CF,k,p|的值迅速增大。也就是说，当周期平均控制在弧长s域中的某谐波角频率kω0接近弹体自身的角运动频率ω1,2时，将会产生共振现象，该频次谐波对应的圆运动的幅值将会异常增大，对弹体控制和飞行产生不利影响。因此在周期平均控制策略设计时，应使各谐波角频率kω0，尤其是低频谐波避开弹体自身的角运动频率。

由于ω1,2>0，因此当k<0时，不会出现因周期平均控制导致共振的情况。而当k>0并且kω0接近ω1,2时，|CF,k,p|异常增大，共振现象发生。

因此，在周期平均控制策略设计中，为了避免共振现象的发生，可选取：

ω0>pω1

(18)

作为周期平均控制角频率ω0的设计条件。其中p应大于1，并且p选取越大，所有kω0将越远离共振频率，设计越保守。

另外，在满足式(18)的设计条件下，当|k|≥2时，|CF,k,p|将远远小于|k|=1时的情况。也就是说，在ω0的设计合理时，对于周期平均控制下的强迫响应ΔF，可以只考虑常数分量引起的动力平衡角和对应基波频率的圆运动，因此在下面的分析中将ΔF近似表示为

ΔF=ΔF,0+CF,-1e-iω0s+CF,1eiω0s

(19)

3 周期平均控制方案

3.1 方案介绍

文献[17-18]中分别介绍了2种周期平均控制方案的思想，将按这2种思想设计的方案分别命名为方案1和方案2，下面简要介绍这2种方案。

如图2所示，顺时针方向为正方向。方案1中，前体的初始滚转角设为γw=γ0，也就是yw轴位于图中A方位，然后以匀速ωa经A和C的中间位置B转过γs到C位置，再反向以匀速ωb转回到A位置，不断重复上述过程。方案1是一种理想方案，未考虑到前体的加减速过程。

方案2对方案1进行了改进。方案2中，前体初始滚转角与方案1相同，然后从静止以角加速度αa从A位置匀加速到B位置，再以αa匀减速到C位置；然后反向从C位置以角加速度αb匀加速到B位置，再以αb匀减速到A位置，再不断重复上述过程。方案2考虑到了前体的加减速过程，更具有工程实用性。

图2 前体滚转角示意图Fig.2 Schematic diagram of roll angle of forward body

3.2 周期平均控制方案角运动强迫响应

计算方案1和方案2在周期平均控制下(式(11)) 的角运动强迫响应，重点是计算如式(8)所示的ck。使用上标(1)和(2)分别表示方案1和方案2的对应计算结果。

1) 方案1

在时域一个周期内，前体滚转角可表示为

(20)

当假设速度为恒定时，弧长可表示为s=Vt，则在弧长s域中前体滚转角可表示为

γw(s)=

(21)

将式(21)代入式(8)，计算得到

(22)

(23)

2) 方案2

在时域一个周期内，前体滚转角可表示为

γw(t)=

(24)

在弧长s域中前体滚转角可表示为

γw(s)=

(25)

(26)

式中：

(27)

3.3 周期平均控制方案对执行机构的要求

式(18)确定了周期平均控制角频率ω0设计的一个下界。由式(15)可见，一般来说ω0的值越大，|CF,k,p|越小，也就是圆运动引起的干扰的幅值越小。但是在实际应用中，执行机构的能力限制了ω0的值不能取的过大，也就是执行机构的能力确立了ω0的设计上界。

一种常见的双旋弹执行机构内部示意图如图3 所示。前体和后体间通过轴承4和轴承7连接，磁钢2和线圈5构成了控制前体滚转通道的电机。执行机构对周期平均控制角频率ω0的限制主要体现在两方面：① 轴承对转速的承受能力，如果前后体间相对转速过高，超过轴承对转速的限制，会造成轴承发热严重，产生卡滞等现象；② 电机的驱动能力，电机需要能产生足够的力矩驱动前体按照周期平均控制的需要转动。

方案1是一种理想的理论方案，并没有考虑到执行机构电机的变速过程，相当于换向瞬间需要执行机构电机提供的力矩为无穷大，实际工程是不可能实现的，只能通过理论仿真实现，因此下面只讨论方案2对执行机构性能的要求。设方案2 中取αa=αb，则易得到方案2中前后体间最大相对转速ωrmax为

(28)

式中：ωAxmax为后体的最大纵轴转速。可见ω0选取的越大，以及在周期平均控制中使用到的γs越大，相对转速ωrmax越大。

电机需要产生的力矩可近似表示为

图3 双旋弹执行机构内部结构示意图Fig.3 Schematic diagram of internal structure of actuator of dual-spin projectile

(29)

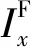
由式(28)和式(29)可见，执行机构的性能确定了周期平均控制角频率ω0的上限。

4 仿真验证

本文以155 mm固定翼双旋弹为例进行仿真。仿真使用的双旋弹参数如下：前体质量为0.235 kg， 后体质量为41.3 kg，前体转动惯量为1.3×10-4kg·m2，后体转动惯量为0.133 kg·m2，弹发射时的初始速度为860 m/s，弹后体的初始转速为230 r/s，射角为47.5°。

仿真时，前60 s无控，前体在气动力矩的作用下反向低速自由旋转。60 s开始控制至落地，取周期平均控制的参数γ0=π/4，γs=π。对于方案1 和方案2，均取T1=0.025 s，T2=0.012 5 s，则在60 s时有ω0≈1.8ω1。此时方案1和方案2周期平均控制下的前体滚转角随时间变化曲线如图4所示。可见，相对于方案1，方案2考虑到了前体的加减速过程。方案1和方案2中|c0|随γs变化的曲线如图5所示。可见，2个方案分别通过在[0,2π]和[0,4.60]区间内调节γs，可以实现在[0,1]区间内调节|c0|。

在上述仿真条件下，选取时间为60 s的时刻，由式(15)计算得到的|CF,k,p|随|kω0|变化的曲线如图6所示。由仿真计算结果可见，当kω0接近ω1,2时，|CF,k,p|异常增大，共振现象发生，与第2节的分析相符。

图4 周期平均控制前体滚转角随时间变化曲线Fig.4 Variation curves of roll angle of forward body with time for period average control

上述仿真条件下的方案1和方案2的合成复迎角曲线如图7所示。图中各画出了3条曲线，1条 是通过式(2)计算的解析结果，在计算过程中每隔0.1 s更新一次方程参数；1条是通过仿真得到的仿真结果，用来验证计算结果的准确性；最后1条 是周期平均等效控制的仿真结果，取等效的同向舵舵偏角为|c0|δw，等效的固定前体滚转角为∠c0。

由图7可见，对于方案1和方案2，计算结果和仿真结果在初始阶段吻合良好，但随时间增加计算结果的误差逐渐积累，会造成计算结果和仿真结果逐渐偏离。当齐次解Δ1对应的两圆运动逐渐收敛后，计算结果和仿真结果又趋于吻合，最后都近似收敛到在复平面上以重力平衡角Δp和周期平均控制动力平衡角ΔF,0的迭加位置为中心点，对应基波频率的两圆运动。仿真结果和等效控制仿真结果的对比进一步展示了周期平均控制对应基波频率的两圆运动的效果，两圆运动的幅度越小，周期平均控制越近似等效控制，也就是周期平均控制的效果越好。

图5 |c0|随γs变化曲线Fig.5 Variation curves of |c0| with γs

图6 |CF,k,p|随|kω0|变化曲线Fig.6 Variation curves of |CF,k,p| with |kω0|

第2节已说明，为了使周期平均控制对应基波频率的两圆运动的幅度较小，周期平均控制的角频率ω0设计时应满足式(18)以避免共振现象的发生。图8给出了方案2中ω0设计不合理时的迎角曲线。在60 s时有ω0≈ω1，ω0处于共振频率附近。由图8可见，设计不合理的ω0会造成过渡阶段的迎角幅值异常增大，并且迎角收敛后周期平均控制对应基波频率的两圆运动的幅值过大，对周期平均控制造成不利影响。

图7 迎角计算值和仿真值结果Fig.7 Analytical and simulation results of angles of attack

图8 方案2共振点附近迎角随时间变化曲线Fig.8 Variation curves of angles of attack with time near resonance for Case 2

5 结 论

1) 本文从双旋弹角运动响应的角度给出了固定翼双旋弹周期平均控制方法设计的理论依据。分析表明，固定翼双旋弹在周期平均控制下的强迫角运动响应为期望得到的动力平衡角和作为扰动的对应各阶次谐波频率的圆运动的迭加。周期平均控制方法设计的原则即为在得到期望的动力平衡角的同时，在考虑执行机构性能限制的条件下，尽可能地减小各阶次干扰圆运动的幅值。

2) 当周期平均控制的角频率设计合理时，可以只考虑对应基波频率的干扰圆运行的影响。以2种周期平均控制方案为例，分析和仿真结果均表明，将固定翼双旋弹在周期平均控制下的受迫角运动响应近似为动力平衡角和对应基波频率的两圆运动的迭加，能够正确反映周期平均控制的本质。

3) 以固定翼双旋弹周期平均控制方法设计原则为指导，得到了周期平均控制角频率选择的条件。为了设计出合理的周期平均控制方案，选择周期平均控制角频率时应以避开弹体共振频率为下界，以执行机构转速限制和转矩限制为上界。设计合理的周期平均控制方案能够有效地解决固定舵控制力幅值不连续可调的问题，为固定翼双旋弹控制与制导方案的设计提供了更多的选择。