自由阻尼梁高频能量流响应的解析模型

滕晓艳，丰国宝，江旭东，赵贺桃

1. 哈尔滨工程大学 机电工程学院，哈尔滨 150001 2. 哈尔滨理工大学 机械动力工程学院，哈尔滨 150080

结构表面阻尼覆层处理，能够有效降低大型幅板、壳体以及桁梁等大尺寸薄壁构件的振动与声辐射。因而广泛应用于空天飞行器、水下潜器和运载车辆中轻质薄壁结构的振动与噪声控制。高频载荷普遍存在于上述轻薄结构的极限工况中，使结构产生显著的高频振动响应，进而导致运载工具内部敏感仪器和电子设备的故障或损伤。因此，形成大阻尼复合结构的高频响应预测模型，评价结构的减振、消振或隔振性能，具有重要的工程应用价值。

近些年来，能量流分析方法已成为预示结构高频振动响应的重要方法。能量流分析方法忽略结构模态的空间分布，以时空平均的能量密度和功率流为基本变量，通过波动在结构中的能量传递特性描述结构的高频振动响应。利用有限元法求解上述能量密度控制方程，将形成能量流分析模型的数值方法——能量有限元法(EFEM)[1]。蔡忠云[2]、孔祥杰[3]、王迪[4]等建立了复合材料结构梁与阻尼结构梁的能量有限元模型，分析了结构的高频能量流响应。Han等[5-6]研究了阻尼、横向运动以及剪切刚度对杆中纵波能量传递与分布特性的影响。葛月等[7]分析了耦合板结构的能量传递系数。孙丽萍[8]和周红卫[9]等推导了耦合板结构弯曲振动的能量密度控制方程，得到了控制方程的有限元解。Navazi等[10]通过实验验证了薄板结构能量有限元模型的有效性。Seo等[11]基于板-梁连接处的功率流耦合关系，求解了板-梁耦合结构的中、高频功率流响应。解妙霞[12]和Kwon[13]等根据薄壳理论和能量平衡关系，推导了圆柱壳及其耦合结构的能量密度控制方程。陈书明[14]、Jandron[15]和Wu[16]等构建了封闭声腔的能量有限元模型，并应用于汽车和水下潜器的振动噪声预报。陈兆林等[17]为了分析结构受到高频冲击载荷激励后的瞬态响应，提出了一种基于EFEM和虚拟模态综合法的高频冲击响应分析方法。Kong等[18]通过混响波场的形成研究了EFEM的有效性，研究结果表明：Le和Cotoni[19-20]推导出基于扩散场的统计能量分析(SEA)准则可以作为评价EFEA有效性的判据。

对于大阻尼结构，结构势能密度和动能密度的时空均值不再满足相等关系，经典的能量流分析模型[1,2,4,6-18]不再适用。文献[3]忽略了结构势能密度和动能密度的不等关系对能量密度控制方程的影响；同时，相比解析模型，形成的能量有限元数值模型也不利于解决大阻尼结构的设计优化问题。文献[5]没有考虑大阻尼复合结构的等效参数对能量密度控制方程的影响，不适于求解自由阻尼结构的高频振动问题。

因此，本文将考虑大阻尼条件下结构势能密度和动能密度的显著差异对系统耗散功率的影响，通过等效刚度法确定附加阻尼结构的等效复刚度和损耗因子，构建大阻尼复合结构的能量密度控制方程，推导阻尼材料不连续处的能量传递特性和耦合关系，解析求解完全自由阻尼梁和局部自由阻尼梁的高频能量流响应。对比提出的能量流解析解与经典的时空平均波动解，检验自由阻尼梁高频能量流响应的解析模型的有效性。

1 完全自由阻尼梁的高频能量流响应

1.1 等效复弯曲刚度与损耗因子

图1为完全自由阻尼梁断面图，基梁表面完全敷设阻尼层。基梁与自由阻尼层的厚度分别为hb和hd，基梁的长度为L，宽度为b，中性层高度为hN。约定在后续的公式推导中，和基梁相关的量以下标s标识，而和阻尼层相关的量以下标d标识，上标*表示物理量的复数形式。

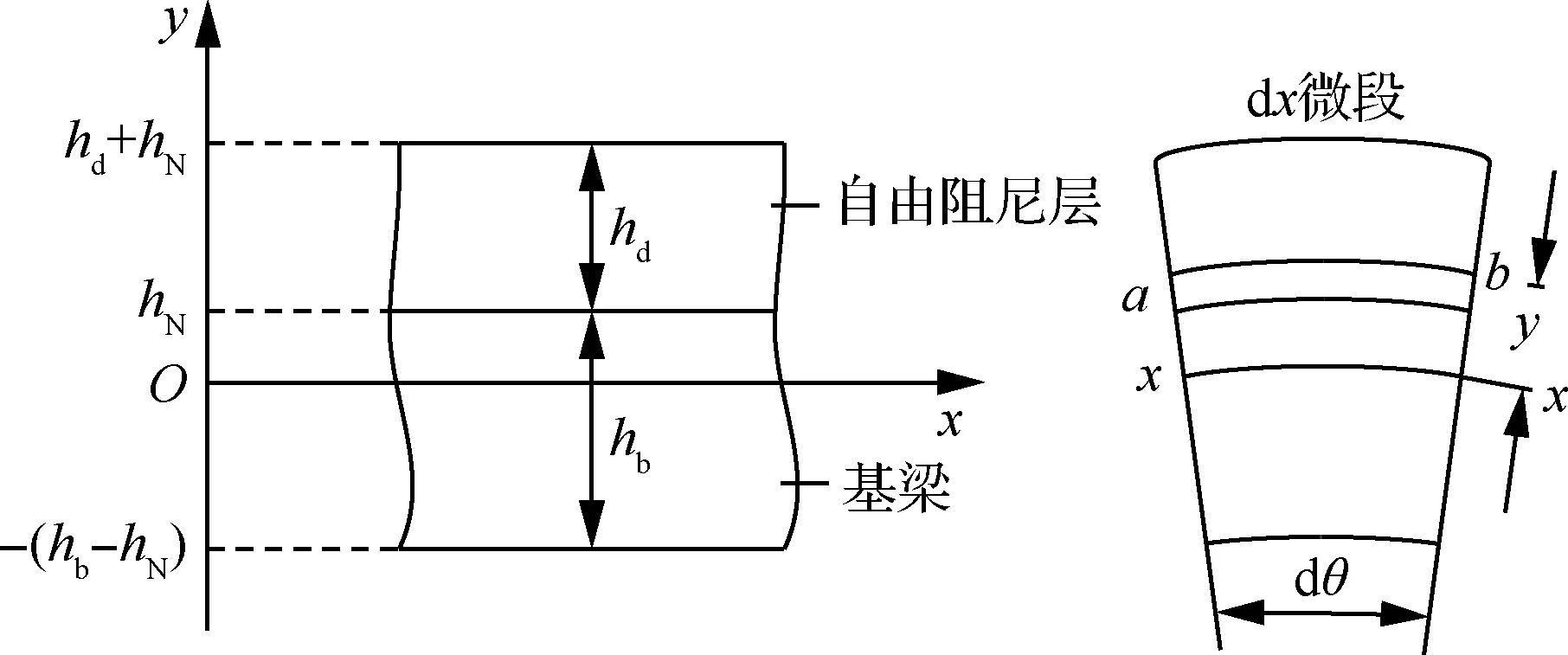
图1 完全自由阻尼梁断面图Fig.1 Section view of a beam with full free layer damping

在dx微段内，弯曲波作用下轴向纤维ab的变形ε与应力σi为

(1)

式中：w(x,t)为完全自由阻尼梁在弯曲波作用下的横向位移;ω为激振力频率;Ei为阻尼层和基梁的弹性模量。

若完全自由阻尼梁内纵向力合力为零，则有

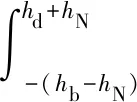
(2)

由此，中性层高度为

(3)

(4)

完全自由阻尼梁内轴截面上的复弯矩与曲率成正比，则有

(5)

式中：Deq为完全自由阻尼梁的等效复弯曲刚度。

将式(1)代入式(4)，并联立式(5)，则有

(6)

由此，完全自由阻尼梁等效复弯曲刚度为

(7)

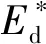
另外，根据等效复弯曲刚度式(7)，完全自由阻尼梁结构的等效损耗因子为

(8)

式中：Re(·)和Im(·)分别为取复数实、虚部的函数。

1.2 能量密度控制方程

图2为完全自由阻尼梁结构，两端简支，基梁长度为L，于x=x0处作用了激振力频率为ω(ω=

图2 完全自由阻尼梁Fig.2 A beam with full free layer damping

2πf)的简谐力F(x0)ejωt，产生的输入功率为πin。

完全自由阻尼梁的横向弯曲振动方程为[3]

(9)

式中：于x=x0处作用的简谐力幅值为F(x0)，meq=ρdSd+ρbSb为完全自由阻尼梁单位长度上的等效质量，其中ρd、ρb分别为阻尼层和基梁的密度，Sd、Sb分别为阻尼层和基梁的横截面积。

根据式(9)，完全自由阻尼梁的横向振动位移的波动解表示为

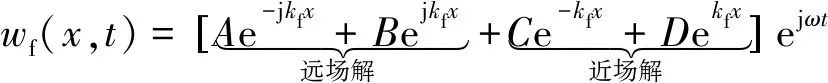
(10)

式中：A、B、C、D为由边界条件确定的待定系数；kf为复弯曲波数，表达式为

(11)

其中：kf1和kf2为复弯曲波数的实部与虚部。

另外，弯曲波在完全自由阻尼梁中复波速表示为

(12)

弯曲波在完全自由阻尼梁传播时，结构的能量密度为弯曲变形能密度Uf和动能密度Vf之和，经时间平均处理后，能量密度表示为[21]

〈ef〉=

(13)

式中：( )′为共轭算子；〈 〉为时间平均算子。

时间平均处理后的能量流表示为[21]

〈qf〉=

(14)

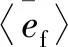
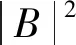
(15)

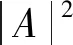
(16)

式中：α1、α2为幅值系数。

联立式(15)和式(16)，能量密度和能量流的时空均值存在如下关系：

(17)

式中：φ=arctanηeq为自由阻尼结构的阻尼角。

另外，类似于结构能量密度的时空平均处理，弯曲变形能密度Uf和动能密度Vf时空均值分别为

(18)

(19)

根据Lase等[22]，系统耗散功率πdiss正比于激振频率和势能密度，则有

πdiss=2ηωU

(20)

式中：U为势能密度。

对于小阻尼结构，动能密度与势能密度相等，式(20)转变为

πdiss=ηωe

(21)

式中：e为结构能量密度。

对于大阻尼结构，式(21)已不再适用，文献[3]的能量有限元模型采用式(21)描述附加自由阻尼结构的耗散功率，忽略了动能密度与势能密度差异对耗散功率的影响。

由此，将大阻尼结构势能密度式(18)代入系统耗散功率式(20)，则有

(22)

对于稳态弹性振动系统，能量流平衡方程表示为

(23)

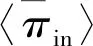
将式(17)、式(22)代入式(23)，完全自由阻尼梁结构的能量密度控制方程为

(24)

对比文献[5]，式(20)充分考虑了大阻尼复合结构的等效参数对能量密度控制方程的影响，更适于描述完全自由阻尼梁的高频能量流特性。

如图2所示，将完全自由阻尼梁劈分为①、②两部分，对应的横向位移分别为wf1(x,t)和wf2(x,t)，交界面x=x0处满足横向位移和转角的连续性，以及弯矩和剪力的平衡条件，则有

wf1(x0,t)=wf2(x0,t)

(25)

(26)

(27)

(28)

因此，联立式(10)、式(25)～式(28)就可获得完全自由阻尼梁的解析波动解。将波动解分别代入到式(13)、式(15)，即可获得完全自由阻尼梁的时域平均波动解与时空平均波动解。

1.3 能量流分析

如图2所示，以简谐力作用点为界限，将组合梁分割为①、②两个子结构。约定下标1、2分别表示依附于梁①、②的各物理量。由式(24)，梁①、②的的能量密度解表示为

(29)

式中：Ffi1、Ffi2为由边界条件确定的待定系数，i=1，2；λf为式(24)的特征值。

将式(29)代入式(24)，则有

(30)

然后，将式(29)、式(30)代入式(17)，能量流表示为

(31)

(32)

对于两端简支边界条件，能量流满足如下边界条件：

(33)

对于系统输入功率作用点，同时满足能量密度连续性条件和能量平衡条件，则有

(34)

(35)

完全自由阻尼梁结构的输入功率为[23]

(36)

由此，联立式(29)～式(36)，确定了完全自由阻尼梁的高频能量流响应。

2 局部自由阻尼梁的高频能量流响应

2.1 能量传递系数

在航空航天工程中，往往在轻薄结构的声振性能最薄弱的区域敷设阻尼层，因而预示局部自由阻尼梁的高频振动具有重要的工程价值。如图3所示，在基梁系统输入功率附近敷设自由阻尼层。当弯曲波传递到阻尼层两端界面时，由于界面附近几何、力学特性的不连续性，入射的弯曲波将产生负向的反射波与正向透射波。因此，将局部自由阻尼梁分割为①～④4个部分，利用能量流平衡关系建立各个子结构的耦合关系，结合能量密为了确定弯曲波在阻尼两端的能量传递特性，分析如图4所示的无限长局部自由阻尼梁结构，在坐标原点处分割为基梁和完全自由阻尼梁，以编号①、②表示两段半无限梁。入射弯曲波A1入射至阻尼界面，在①中产生负向反射波B1和渐逝波D1，在②中形成正向透射波A2和渐逝波C2。

图3 局部自由阻尼梁Fig.3 A beam with partial free layer damping

度控制方程求解局部自由度阻尼梁的能量流响应。另外，约定下标1～4分别表示依附于梁①～④的各物理量。

由此，半无限梁①、②的横向振动位移的波动解表示为

(37)

(38)

式中：A1、B1、D1和A2、C2为待定系数；kfb为基梁(半无限梁①)的弯曲波波数。

阻尼交界面x=0处满足横向位移和转角的连续性，以及弯矩和剪力的平衡条件，则有

(39)

(40)

(41)

(42)

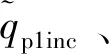
(43)

在阻尼交界面x=0处的入射弯曲波、反射弯曲波和透射弯曲波满足如下能量平衡关系：

(44)

将式(37)、(38)代入式(39)～式(42)，并结合式(43)，可得半无限梁①至②的弯曲波能量流透射

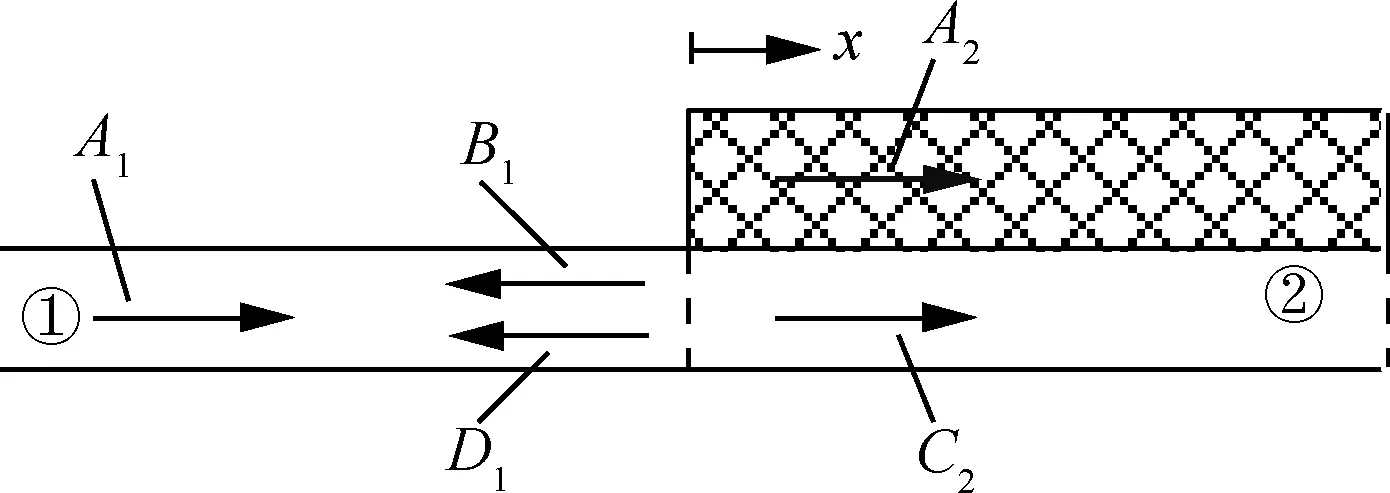
图4 弯曲波的透射与反射Fig.4 Transmitted and reflected flexural waves

系数τff12、反射系数γff11分别为

(45)

(46)

2.2 能量流分析

对于两端简支边界条件，图3中梁①和④能量流qp1、qp4满足如下边界条件：

(47)

对于系统输入功率作用点，图3梁②、③的能量密度ep2、ep3，功率流qp2、qp3分别满足能量密度连续性条件和能量平衡条件，则有

(48)

(49)

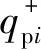
(50)

对于梁①和②交界面x=x1处，流出交界面一侧的能量平衡关系为

(51)

(52)

式中：γff22为梁②至①的弯曲波能量流反射系数，τff21为梁②至①的弯曲波能量流透射系数。

对于梁③和④交界面x=x2处，流出交界面一侧的能量平衡关系为

(53)

(54)

式中：γff33、γff44分别为梁③至④，梁④至③弯曲波能量流的反射系数；τff34、τff43分别为梁③至④，梁④至③弯曲波能量流的透射系数。

另外，结合式(44)～式(46)，对于保守的一维振动梁结构系统，能量传递系数满足如下关系：

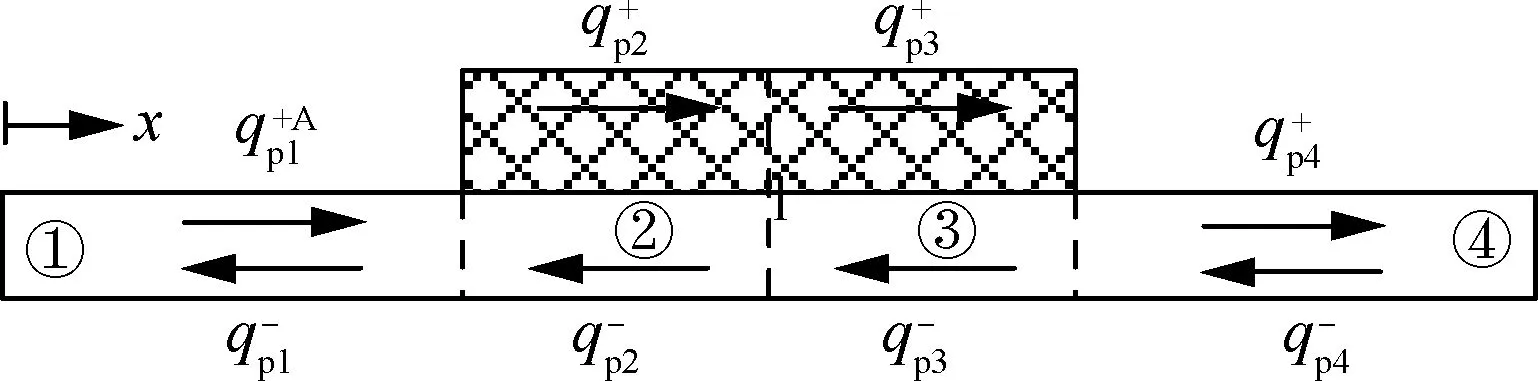
图5 弯曲波能量传递Fig.5 Power transfer of flexural wave

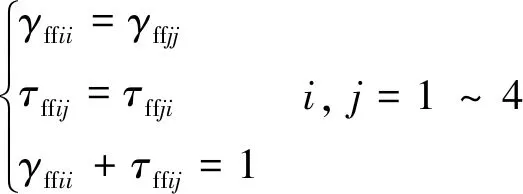
(55)

由此，联立式(31)、式(36)以及式(47)～式(55)，则可求解局部自由阻尼梁的高频能量流响应。对于局部自由阻尼梁的波动解，利用①～④交界面处的连续性条件与平衡条件，结合波动解的形式获得。

3 数值算例

为了检验提出的自由阻尼梁高频能量流响应的解析模型的有效性，以完全自由阻尼梁和局部自由阻尼梁结构为数值算例，对比分析上述2种典型工程结构的能量流解析解和时空平均的波动解。其中，时空平均的波动解为其时域平均的能量密度在本地一个波长的空间平均。

3.1 完全自由阻尼梁

完全自由阻尼梁中心承受幅值F=1 N的简谐载荷(如图2所示)，激振频率f=0.5、2、4、6 kHz， 能量密度参考值eref=10-12J/m。基梁的长度L=1 m，宽度b=0.008 m，厚度hb=0.002 m。基梁结构的材料密度ρb=2 700 kg/m3，弹性模量Eb=71 GPa，损耗因子ηb=0.01。自由阻尼层的厚度hd=0.004 m，材料密度ρd=980 kg/m3，弹性模量Ed=0.33 GPa，损耗因子ηd=1.3。

能量流解析模型的能量密度表征某一点附近一个波长内的能量密度均值，因而并不代表该点的能量密度均值。图6为完全自由阻尼梁在不同激振频率简谐力作用下的能量密度分布，能量流解析解反映了时空平均波动解的整体变化趋势，而且随着激振频率的增加，两者的差异逐渐减小。同时，由于载荷、边界与结构的对称性，高频能量流响应呈现对称关系。此外，由于能量流解析解忽略了近场解的影响，在激励作用点和两端约束处与时空平均波动解的差异最大。

3.2 局部自由阻尼梁

如图3所示，局部自由阻尼梁的中部区域(0.25～0.75 m 区间)敷设黏弹性自由阻尼层，结构其它几何尺寸，材料特性以及载荷工况均与完全阻尼梁结构相同。

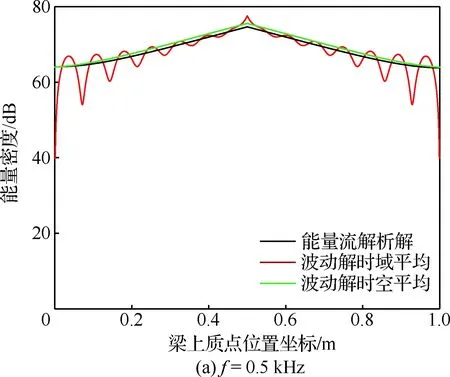
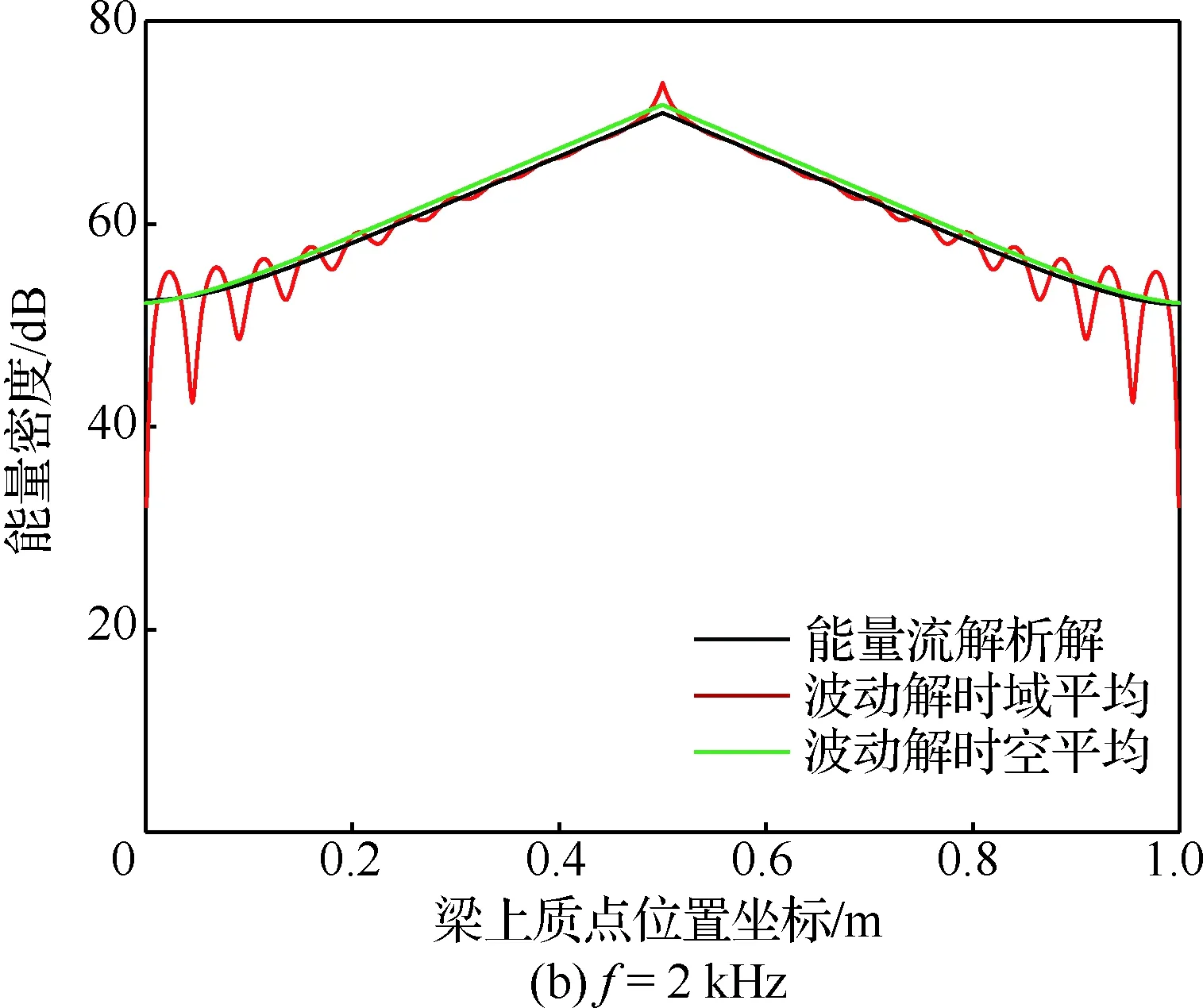
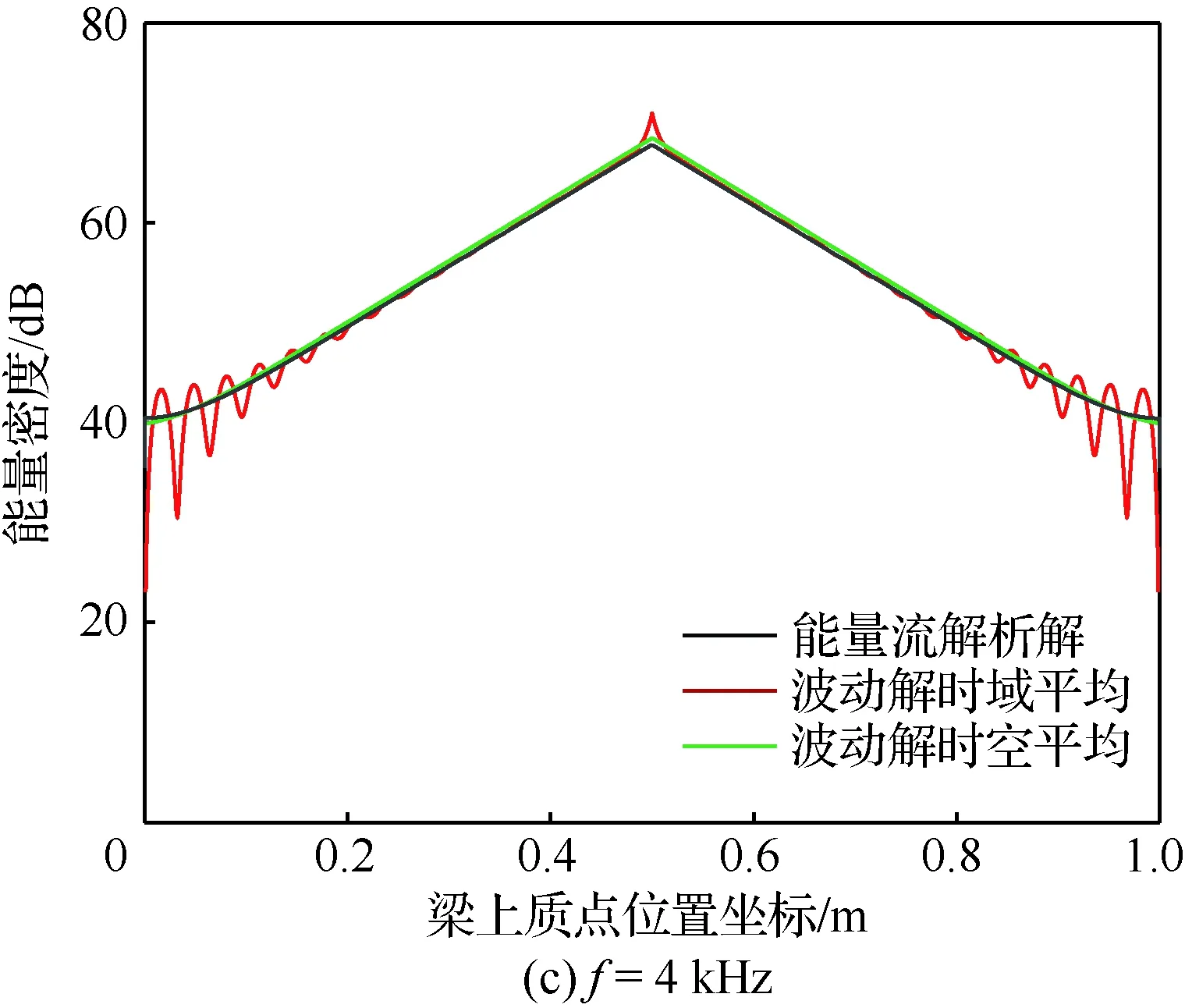
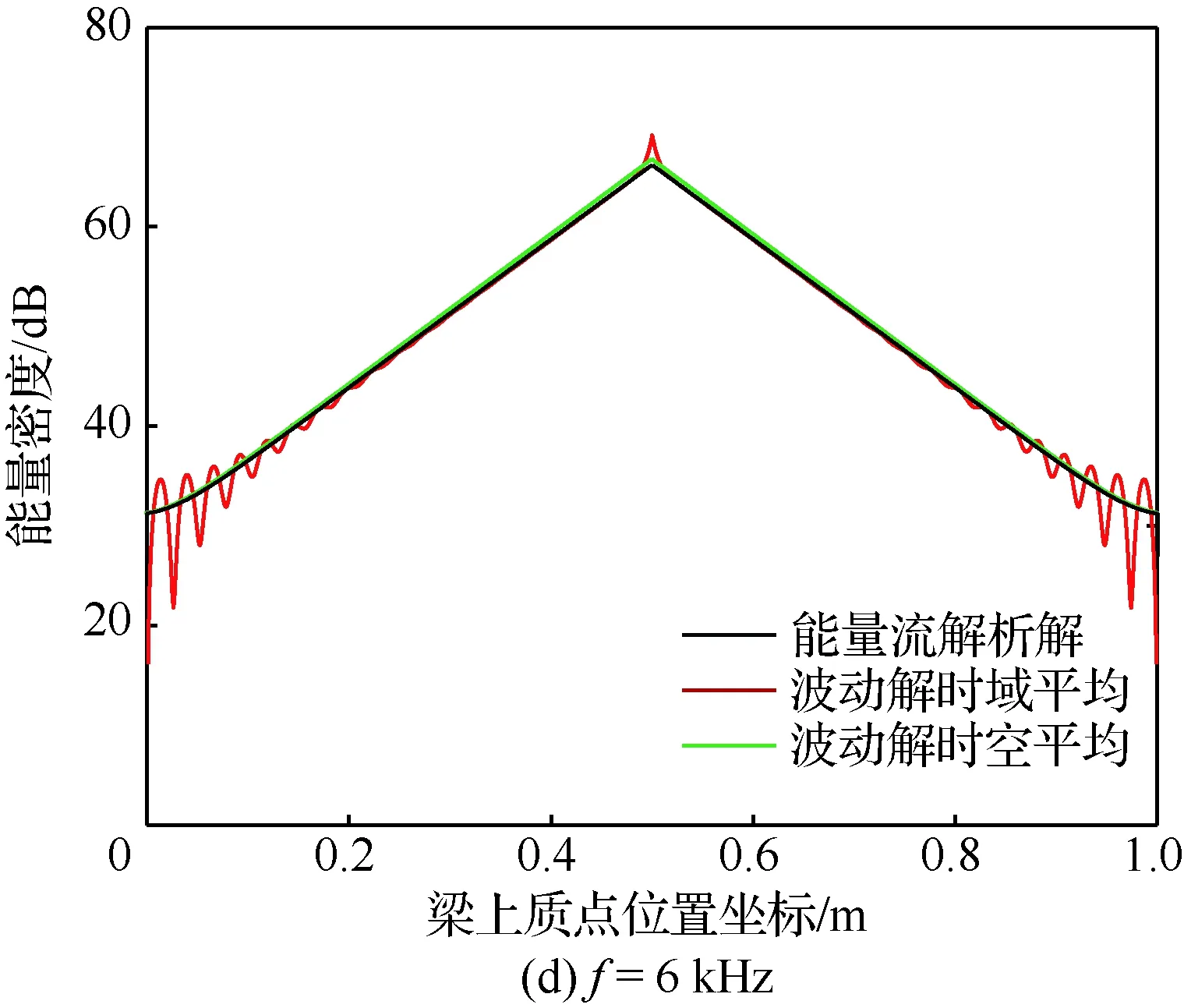
图6 不同激振频率下完全自由阻尼梁的能量密度分布Fig.6 Energy density distribution of a beam with full free layer damping under different excited frequency

图7为局部自由阻尼梁在不同激振频率简谐力作用下的能量密度分布，与完全自由阻尼梁相比，阻尼层长度的减小削弱了能量衰减作用，引起局部自由阻尼梁的振动更为剧烈；在阻尼层的两端，波数的改变引起能量密度的不连续。能量流解析解仍然反映了时空平均波动解的整体变化趋势，随着激振频率的增加，两者的差异逐渐减小。鉴于载荷、边界与结构的对称性，高频能量流响应呈现对称关系。由于能量流解析解忽略了近场解的影响，在阻尼层两端和两端约束处与时空平均波动解的差异最大。

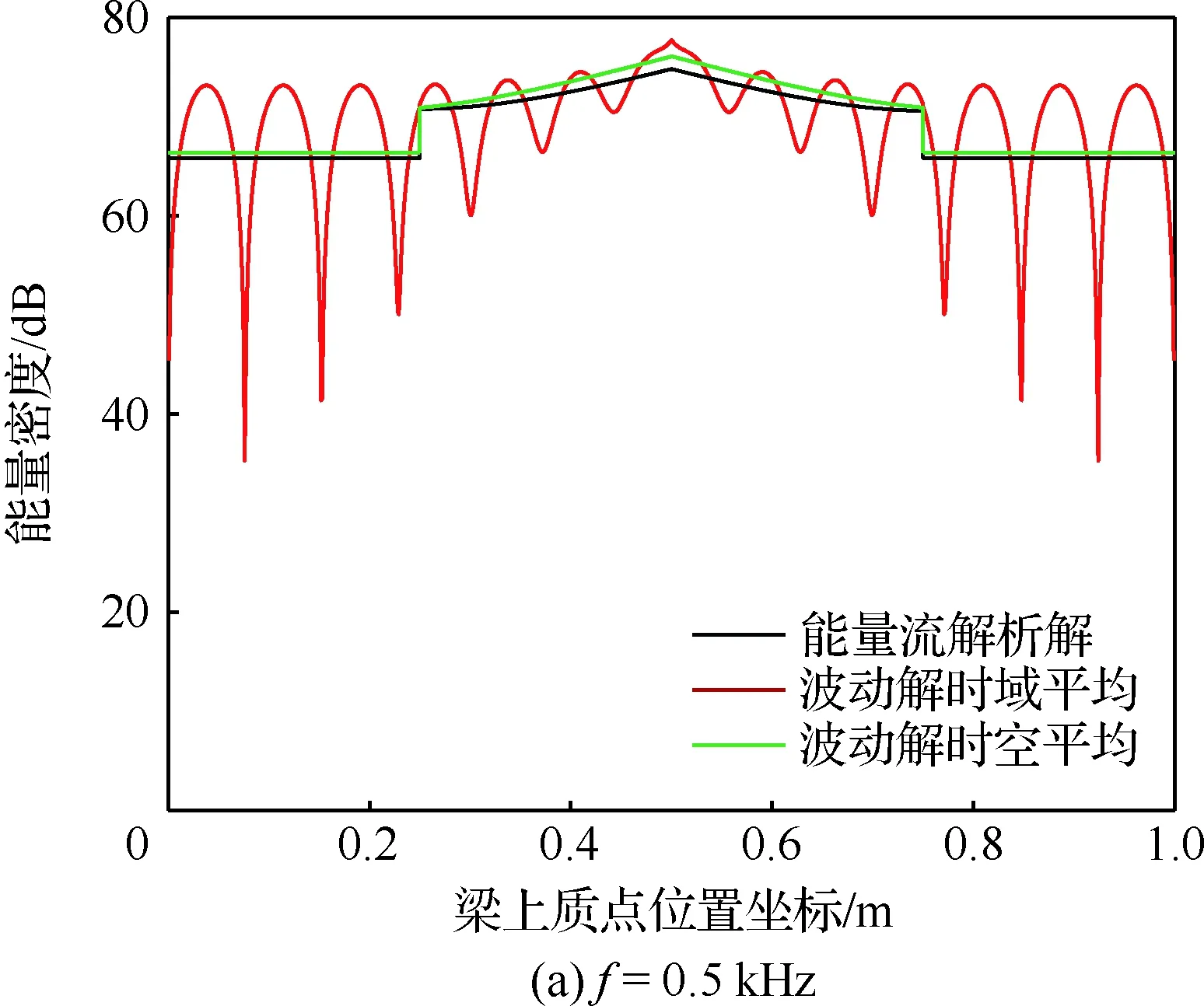
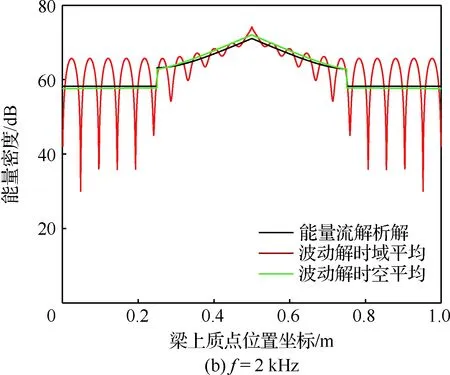
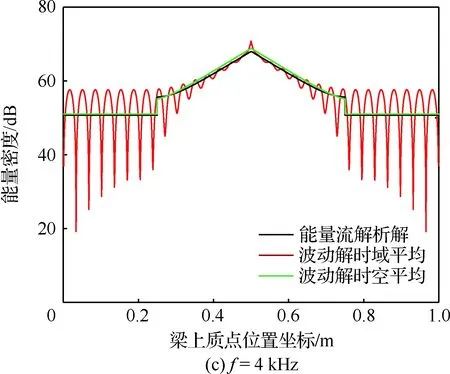
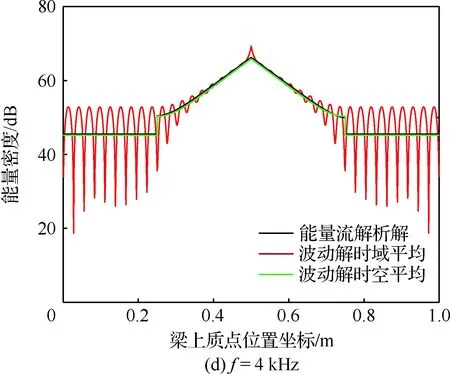
图7 不同激振频率下局部自由阻尼梁的能量密度分布Fig.7 Energy density distribution of a beam with partial free layer damping under different excited frequency

由此，通过以上典型算例，本文提出的能量流解析模型能够较为精确地预测自由阻尼梁等大阻尼结构的高频能量流响应，反映结构高频振动下的能量分布规律。

4 结 论

为了预测自由阻尼梁在高频激励下的振动响应，推导了大阻尼复合结构的能量密度控制方程，对比分析了本文提出的能量流解析解与经典的时空平均波动解，获得了如下的研究结论：

1) 构建了完全自由阻尼梁的高频能量流解析模型，求解了结构的高频振动特性。数值结果表明，能量流解析解与经典的时空平均波动解一致，而且随着激振频率的增加，两者差异逐渐减小。

2) 分析了弯曲波在阻尼结构耦合处的能量传递特性，构建了局部自由阻尼梁的高频能量流解析模型，求解了结构的高频振动特性。数值结果表明，随着激振频率的增加，能量流解析解与经典的时空平均波动解一致逼近，计算误差逐渐减小。

综上，本文提出的解析模型为能量流分析方法应用于大阻尼复合结构的高频振动响应预报提供了借鉴，为结构的阻尼减振设计优化提供了可靠的计算模型。