空间对称型7R机构运动特性分析及组合应用

韩博，许允斗,2，姚建涛,2，郑东，张硕，赵永生,2,*

1. 燕山大学 河北省并联机器人与机电系统实验室，秦皇岛 066004 2. 燕山大学 先进锻压成型技术与科学教育部重点实验室，秦皇岛 066004

空间可展开机构可以在储存和运输时处于收拢状态，占据运载装置较小的空间，当需要工作时可完全展开，这种特点使得其在航空航天领域得到了广泛的应用，如俄罗斯“联盟号”飞船上的可展开天线[1]、日本ETS-Ⅷ卫星天线[2]、美国AstroMesh可展开天线[3]以及中国的HJ-1-C卫星SAR天线[4]等，已逐渐成为航天领域的研究热点之一。

目前，国内外相关学者已针对空间可展开机构进行了一系列的研究，取得了较多研究成果。Lu等[5]采用Hoekens直线单元机构组成了一种平面可展天线结构，杨毅和张武翔[6]通过组合空间对称型6R(R表示转动副)机构得到了一类平板式可展开天线机构， Vu等[7]基于金字塔式可展开单元组合得到了多种平面可展开天线机构，文献[8-9]研究了Bricard和Bennett连杆机构在空间可展开机构中的应用，文献[10]和文献[11]分别基于剪叉机构和Myard机构构造了大型可展开天线机构，文献[12-15]也分别研究构造了多种类型的空间可展开机构。

随着空间可展开机构的应用越来越多，一些学者针对此类机构的运动特性也进行了相关研究，文献[16]和文献[17]分别研究了一类空间多面体向心机构和四棱锥平板单元的运动特性，并基于此构造了一种空间伸展臂以及平板式空间可展开天线机构，许允斗等[18]针对大型构架式空间可展开天线提出了一种拆杆等效的自由度分析方法，该方法针对空间多环耦合机构具有较高的通用性，Zhao[19]和李端玲[20]等利用螺旋理论，分别分析了平面型和球面型剪叉机构的运动特性问题，Wei等[21]基于螺旋理论和图论分析了魔术花球机构的自由度问题，文献[22]和文献[23]基于螺旋理论分别分析了剪叉机构组合单元的自由度、运动学以及动力学等问题，史创等[24]针对一种双层环形桁架式可展开机构进行了机构设计与力学分析。

空间可展开机构多由空间连杆机构组合而成，7R机构是空间连杆机构中重要的一类，可作为串联机构应用于机械臂上，也可经首尾相连后组成闭环机构进而组合成为空间可展开机构，文献[25-27]研究了7R机构在机械臂中的运动控制与轨迹规划问题，霍希建等[28]研究了7R机构在仿人机械臂中的应用；在闭环机构方面，郭盛等[29]研究了包含7R机构在内的单闭环过约束机构的构型综合问题，Deng等[30]系统地研究了5R～8R 单闭环可展开机构的综合与几何设计方法，并给出了包含7R机构在内的多种单闭环可展机构的几何形貌。通过以上文献的研究可以发现，现有研究对串联式7R机构的研究较为深入透彻，但是对闭环7R机构的运动特性的研究较少，关于闭环7R机构的组合应用的相关研究鲜有报道。

本文提出了一种空间对称型7R机构，可用来构造空间可展开机构，结合图论与螺旋理论[31]分析了机构的整体自由度、运动输出构件自由度、奇异性等运动特性，获得了运动副轴线不同方位情况下运动输出构件的机构自由度性质，并对其瞬时性做了判别，同时分析了机构在不同驱动情况下的奇异特性，得到了机构在不同的驱动下处于奇异位形时的几何条件，最后基于此空间对称型7R机构，组合得到了一类在完全展开时具有较好的力学性能的空间多棱锥可展开机构，可较好地应用于航空航天领域。

1 空间对称型7R机构构型描述

空间对称型7R机构的结构图及其机构简图如图1所示，其包括E、A、B、C1、C2、D1、D27根连杆，7根连杆通过S1～S77个转动副铰链连接，其中转动副轴线S1和转动副轴线S2、S7均平行，转动副轴线S3和轴线S4平行，转动副轴线S5和轴线S6平行，且转动副轴线S4和S5共面，整个7R机构关于过转动副轴线S1且垂直于连杆E的平面对称。

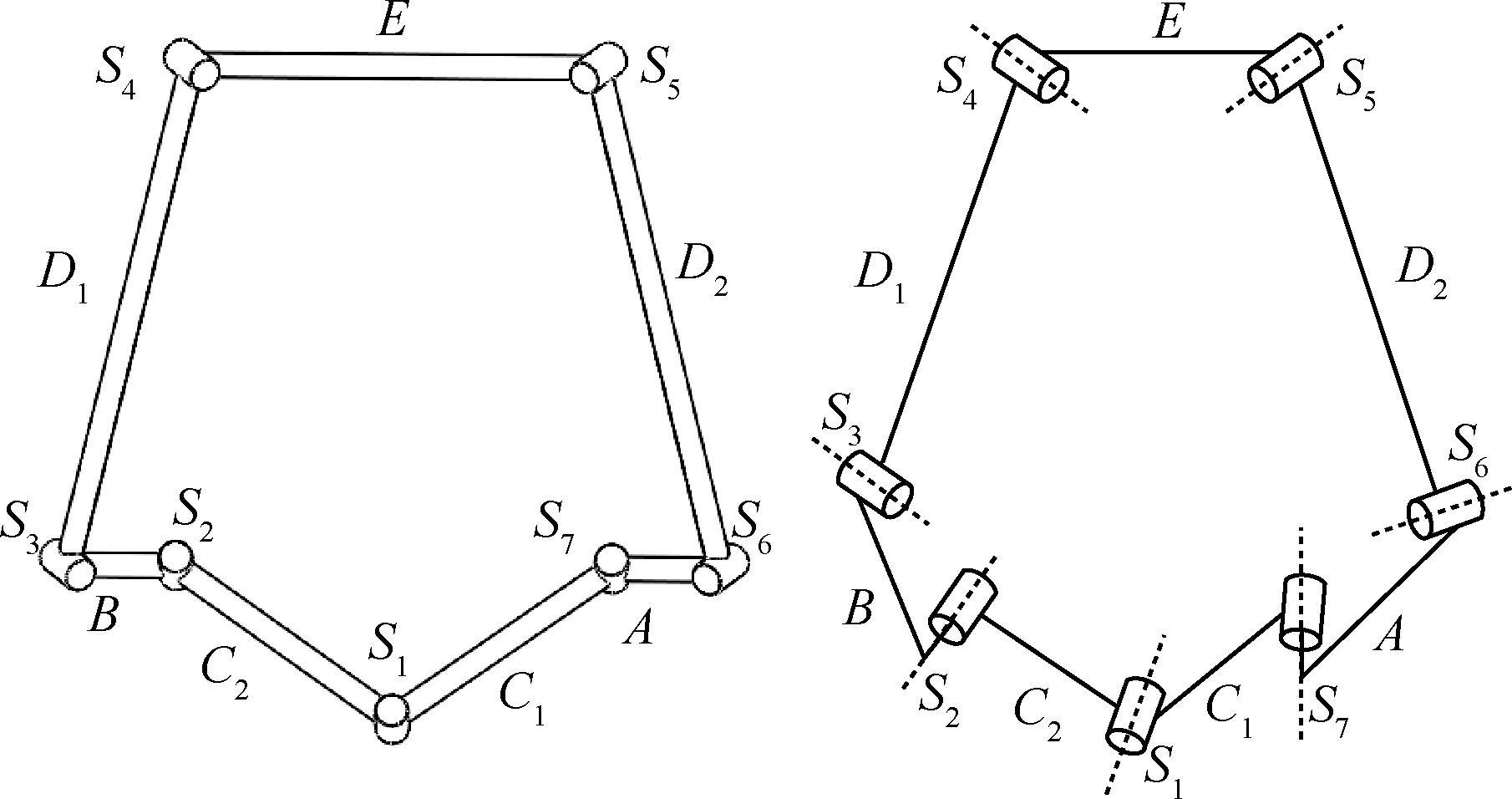
图1 空间对称型7R机构Fig.1 Spatial symmetric 7R mechanism

空间对称型7R机构位置坐标系如图2所示，坐标系原点O位于连杆E竖直方向的中垂线和铰链S2S7中心点连线水平方向的中垂线的交点上，X轴平行于铰链S2S7中心点连线，方向由铰链S2的中心点指向S7的中心点，Z轴垂直向上，Y轴指向由右手定则确定，整个机构关于YOZ平面对称。

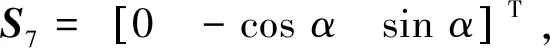
图2 位置坐标系Fig.2 Position coordinate system

文献[30]的图6中曾给出了几种7R机构的几何形貌，但与此空间对称型7R机构形貌不同，其运动副轴线方位及机构对称性与此机构亦不相同。由图1可以看到，此空间对称型7R机构含有C1、C2和D1、D2等4根两端转动副均平行的连杆，以及A、B、E等3根两端转动副不平行的连杆，其中A与B两个构件两端的转动副轴线异面布置，这是此机构的特点，可以利用此特点，以A、B和E这3个构件作为复杂形体的节点连接件，利用C1、C2和D1、D2连杆作为展开收拢运动连杆，组合不同类型的空间可展开机构单元。

2 自由度分析

机构的自由度数为确定机构或运动链位形的独立参数的数目，亦即确定机构整体运动所需的输入的个数。对于空间环路机构而言，除需要计算整体机构自由度数目之外，还应关注机构中运动输出构件的自由度性质，才能更好地应用此机构。由于空间对称型7R机构关于YOZ平面对称，当采用此机构组合空间可展开机构时，可利用其空间面对称性，将构件E作为运动基础构件(即机架)，选择对称的构件A和构件C作为运动输出构件，因此下面将分析整体机构自由度数以及运动输出构件的自由度，这样可以更清晰准确地认识空间对称型7R机构的自由度特性。

2.1 整体机构自由度分析

空间对称型7R机构的旋量约束拓扑图如图3所示，在拓扑图中，节点表示机构中对应的构件，连线表示对应的铰链。

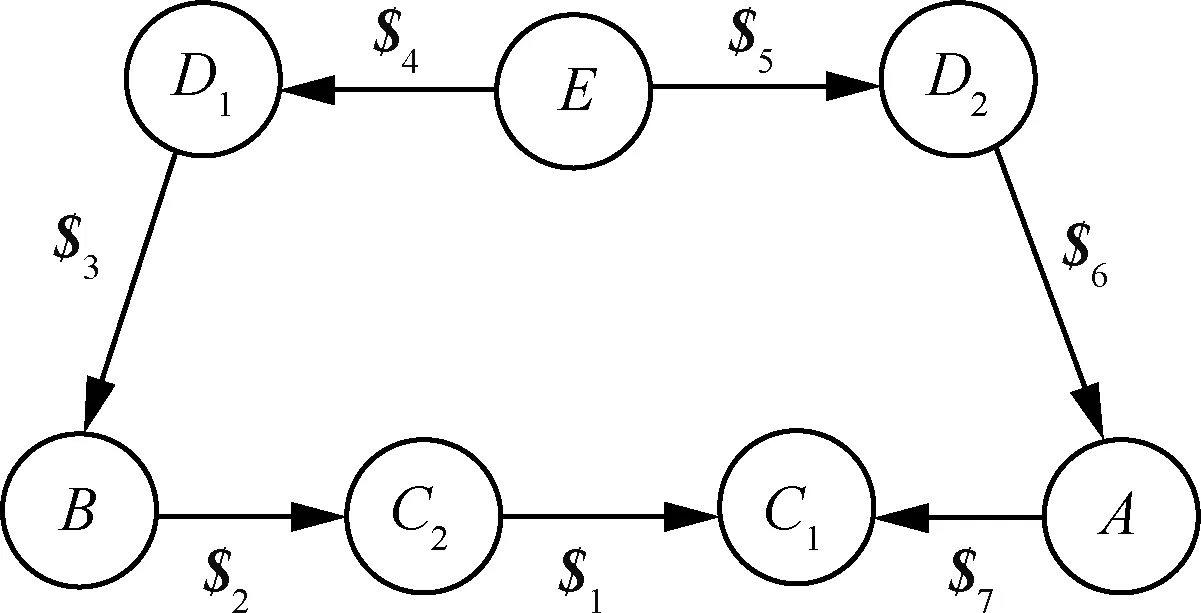
图3 旋量约束拓扑图Fig.3 Schematic diagram of screw constraint topology

根据前面得到的各个铰链中心点的位置坐标以及轴线方向矢量，可以得到各个铰链的运动螺旋表达式为

(1)

用ω表示转动副的角速度大小，$表示相应的单位运动旋量，下标表示相应的运动副，则在此机构对应的旋量拓扑图所示的环路中，闭环旋量方程可以表示为

ω4$4+ω3$3+ω2$2+ω1$1-

ω5$5-ω6$6-ω7$7=0

(2)

式中：0为6维列向量。

将上述约束旋量方程组写成矩阵的形式：

Mω=0

(3)

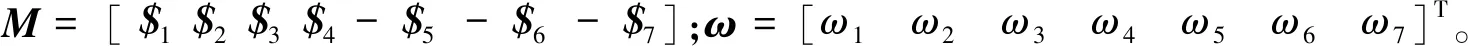
旋量约束矩阵M是一个6×7维矩阵，机构自由度数对应于约束矩阵的零空间的维数，通过分析其旋量约束矩阵的秩rank(M)可以计算得到其对应的零空间的维数。由于此机构中α与β数值未知，都可以在0°～180°之间变化，亦即此机构中运动副轴线方位布置可以变化，因此可以将α与β视为两个变量，将式(1)中各个运动螺旋代入式(3)中的旋量约束矩阵M中，通过MATLAB软件编程计算，得出当α与β分别在0°～180°之间变化时，旋量约束矩阵M的秩的变化情况，从而分析运动副铰链轴线方位布置对整体机构自由度数目变化的影响。

当α与β分别在0°～180°之间变化时，旋量约束矩阵M的秩的变化情况如图4所示。

图4 旋量约束矩阵的秩Fig.4 Rank of screw constraint matrix

由于旋量约束矩阵M是一个6×7维矩阵，零空间的维数为其列数减去秩，即7-rank(M)，因此根据图4可得：

1) 当角度α与β均为0°或者180°时，此时铰链轴线S1～S7均平行于Y轴，旋量约束矩阵M的秩为3，所以其自由度数为4，需要4个输入才能完全确定整体机构的运动。

2) 当α与β中有一个为0°或180°，另一个为0°～180°之间的值时，约束旋量矩阵M的秩为5，此时其自由度数为2，需要两个输入才能完全确定整体机构的运动。

3) 当α与β均为0°～180°之间的值时，约束旋量矩阵M的秩为6，此时其自由度数为1，只需要一个输入就能完全确定整体机构的运动。

分析以上结果可以看出对于空间对称型7R机构，其运动副轴线方位布置不同，会导致机构自由度发生变化，且主要在角度α与β取0°或180°时自由度数目发生突变。

2.2 运动输出构件自由度分析

将构件E作为机架，选择对称的构件A和构件C作为运动输出构件，二者的运动性质也关于YOZ平面对称。下面将采用反螺旋理论分析运动输出构件A在不同运动副轴线方位布置情况下的自由度数目和性质，并判断其瞬时性。

2.2.1α=β=0°,180°

此时铰链轴线S1～S7均平行，且平行于Y轴，此机构变为平面7R机构，如图5所示。

图5 平面7R机构Fig.5 Planar 7R mechanism

此时各个运动旋量的表达式为

(4)

此机构可等效为一个两分支并联机构，两个分支分别为5R分支和2R分支，5R分支的运动螺旋系为

(5)

2R分支运动螺旋系为

(6)

分别求取两个分支的约束螺旋系并组合得到运动输出构件的整体约束螺旋系为

(7)

对整体约束螺旋系再次求反螺旋可得输出构件的运动螺旋系为

(8)

根据2.1节中的计算结果，此时整体机构自由度数为4，通过式(8)分析可知此时运动输出构件的自由度数为2。通过分析式(5)中运动螺旋系可知，运动螺旋的数量为5，但是其最大线性无关组为3，因此具有两个局部自由度，所以虽然运动输出构件只具有两个自由度，但是确定整个机构运动仍需要4个输入，整体机构自由度数目为4，其中两个自由度为不影响机构输出件运动的自由度，即局部自由度。

由于此时机构为全R副平面机构，在机构任何可能的运动过程中，各个分支的运动副因为结构的限制总保持原有的几何关系，应用反螺旋理论分析得到的分支约束力螺旋系不变，所以运动输出构件的自由度不会发生改变，因此，此时计算得到的运动输出构件的自由度是全周性的。

2.2.2α=0°,180°，β=0°～180°

此时铰链轴线S1∥S2∥S7，且平行于Y轴，仍然将此机构等效为含两个分支的并联机构，两个分支分别为5R分支和2R分支，5R分支的运动螺旋系为

(9)

2R分支运动螺旋系为

(10)

分别求取两个分支的约束螺旋系并组合得到运动输出构件的整体约束螺旋系为

(11)

对整体约束螺旋系再次求反螺旋可得输出构件的运动螺旋系为

(12)

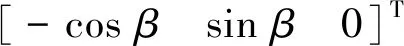
(13)

2R分支运动螺旋系为

(14)

分别求取两个分支的约束螺旋系并组合得到运动输出构件的整体约束螺旋系为

(15)

对整体约束螺旋系再次求反螺旋可得输出构件的运动螺旋系为

(16)

2.2.3β=0°，180°，α=0°～180°

此时铰链轴线S3∥S4∥S5∥S6，且平行于Y轴，5R分支的运动螺旋系变为

(17)

2R分支运动螺旋系为

(18)

分别求取两个分支的约束螺旋系并组合得到运动输出构件的整体约束螺旋系为

(19)

对整体约束螺旋系再次求反螺旋可得输出构件的运动螺旋系为

(20)

分析式(20)中的运动螺旋可知，运动输出构件具有两个运动自由度，分别为绕YOZ平面内过点(0,x3z4/(x3-x4))且平行于Y轴直线的转动和沿与连杆D2垂直方向的移动。

由于机构在上述的一个转动和一个移动的运动过程中，各个分支的运动副因为结构的限制总保持原有的几何关系，应用反螺旋理论分析得到的分支约束力螺旋系不变，所以运动输出构件的自由度不会发生改变，因此，此时计算得到的运动输出构件的自由度是全周性的。

2.2.4α,β=0°～180°

此时为最一般的情况，机构5R分支的运动螺旋系变为

(21)

2R分支运动螺旋系为

(22)

分别求取两个分支的约束螺旋系并组合得到运动输出构件的整体约束螺旋系为

(23)

对整体约束螺旋系再次求反螺旋可得输出构件的运动螺旋系为

(24)

由以上分析可得，对于此对称型空间7R机构而言，其运动副轴线方位布置的不同会影响机构整体机构自由度，同时也会令运动输出构件产生瞬时自由度，综合以上4种情况可知，当此机构中夹角β不为0°或180°时，无论夹角α值为多少，运动输出构件均只有一个移动自由度，此时整体机构亦只需一个输入便可确定整个机构的运动位形，这为后续由此机构组合构造空间可展开机构单元奠定了基础。

3 奇异特性分析

由于此空间对称型7R机构关于YOZ平面对称，其各个构件的运动轨迹也关于YOZ平面对称，如图6所示，构件E和铰链S3以及铰链S1分别沿轴线M1O、M2O、M3O1作平移运动，因此可以将此空间对称型7R机构进一步简化为一个4R3P(P表示移动副)机构。

由于此空间对称型7R机构可以等效简化为一个4R3P机构，等效后其各个构件的运动并无变化，因此可以通过分析此4R3P机构的奇异特性来得到空间对称型7R机构的奇异特性。不失一般性，可以通过分析不同驱动输入条件下4R3P机构的奇异位形来得到空间对称型7R机构运动过程中的所有奇异位形。机构在正常位形下时，雅克比矩阵满秩，行列式值不为零，当处于奇异位形时，雅克比矩阵欠秩，行列式为零，因此可以通过图6中的封闭环路，列写此机构满足的环路约束方程组，进而得到机构在不同驱动下的雅克比矩阵或其逆矩阵，通过其行列式为零值的条件计算得到机构在不同输入下奇异位形所出现的几何条件，分析其奇异特性。

在图6中，θ1为平移轴线M1O和连杆D1轴线之间的夹角，θ2为平移轴线M3O1和连杆C2轴线之间的夹角，杆件E的杆长为l1，杆件D1、B和C2的杆长分别为l2、l3和l4，图中各个转动副中心点分别用H1～H4表示，E杆中心点用H5表示；移动副OH5、OH2和O1H4的长度分别为n1、n2和n3。

图6 4R3P机构及其机构简图Fig.6 4R3P mechanism and its schematic diagram

在四边形OH5H1H2中，可得

(25)

即

(26)

对式(26)求导可得

(27)

在三角形OO1H2和三角形O1H3H4中，可以得到

(28)

即

(29)

对式(29)求导可得

(30)

因此可以得到θ1和θ2之间的关系：

(31)

将式(27)和式(30)整理可得

(32)

将式(32)写成矩阵的形式，可以得到

(33)

式中：0为五维列向量。

下面讨论此机构在不同驱动条件下的奇异性问题。

(34)

方程左侧系数矩阵的逆矩阵为此4R3P机构在轴线M1O上添加驱动时的速度雅克比矩阵，当速度雅克比矩阵欠秩导致行列式的值为0时，此矩阵的行列式也必为0，因此可以通过分析此矩阵的行列式的值为0时的几何条件来得到此机构的奇异位形点。

(35)

式中：J为雅克比矩阵的逆矩阵。

式(35)矩阵行列式值为|J|=-l2l4cosθ2sinθ1，当机构处于奇异位形时，|J|=0，代入前述关系式整理得

|J|=-l2l4cosθ2sinθ1=

-l4cosθ2[(l3+l4sinθ2)/cosβ-l1/2]=0

(36)

综合分析以上5种情况可知，在不同的驱动情况下，此机构的奇异位形点均发生在夹角θ1和θ2取0°或者90°时，这是此空间对称型7R机构的特点，在用其组合构造空间可展开机构时，可充分利用此机构的奇异点特性并在机构运动过程中间避开其奇异位形点。

4 组合应用

应用此7R机构组合空间可展开机构时，由于运动副轴线方位布置会影响机构自由度，考虑到航天应用对大型空间可展开机构简单可靠的要求，选用自由度少且无局部自由度的运动副轴线方位布置。根据本文第2部分的分析，当此机构中夹角β不为0°或180°时，运动输出构件均只有一个自由度，且此时整体机构只需一个输入便可确定整个机构的运动位形，因此选定此种情况时的7R机构来组合构造空间可展开机构。

针对运动构件A与B而言，二者的相对运动为沿位于XOY平面上与Y轴平行的直线的相互靠近或远离，而这正是空间可展开机构中节点花盘构件间的相互运动，同时针对整体机构而言，两个运动构件在XOY平面上向坐标原点O靠拢或远离的同步运动，这与空间可展开机构中可展单元平面向心收拢的运动相同，考虑到夹角α与β角度数值可变，以及机构含有的连杆D1和D2，因此可以通过组合多个此7R机构来组合构造空间多棱锥可展开机构。

由于夹角α的大小并不影响机构自由度，因此可以随意设置，当组合多棱锥可展开机构时，通过β角取不同的值，可以通过7R机构组合构造不同的空间多棱锥可展开机构，当α角取0°，β角分别取30°、45°以及60°时，通过此空间对称型7R机构组合得到的空间三棱锥、四棱锥以及六棱锥机构如图8所示。

由图8可以看到，每个7R机构位于棱锥机构的一个侧面，由于运动副的约束关系，每个7R机构的两个运动输出构件的运动是同时的，由于两个侧面的7R机构共用一个运动输出构件，因此整个空间多棱锥机构中运动输出构件的运动均为同时的，所以空间多棱锥机构的整体自由度与单个7R机构相同，空间多棱锥机构整体亦为单自由度机构。

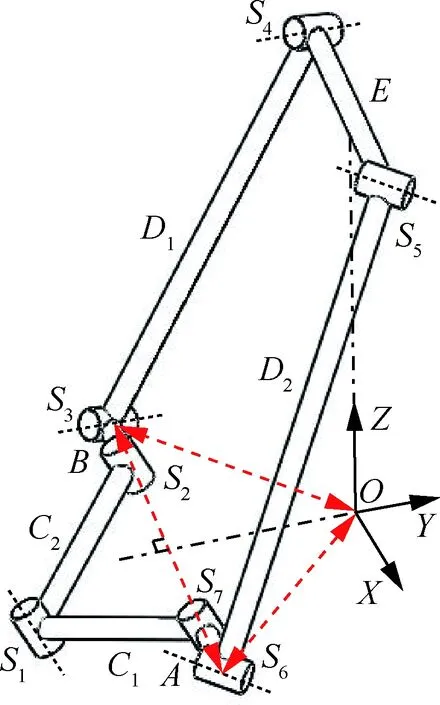
图7 构件A和B的运动轨迹示意图Fig.7 Schematic diagram of motion trajectories of components A and B

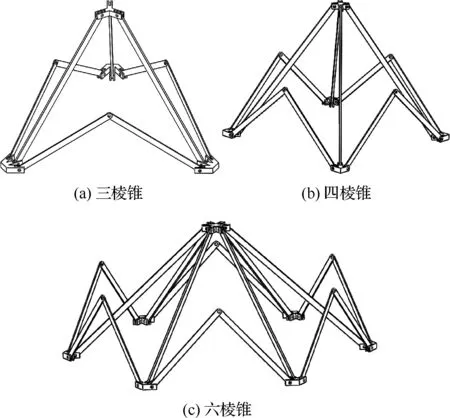
图8 由7R机构单元构造的多棱锥机构Fig.8 Polygonal pyramid mechanisms constructed by 7R mechanism unit

以空间六棱锥机构为例，分析角度α的取值对空间多棱锥机构收拢率的影响。设定空间六棱锥机构棱边杆件长度为h，收拢后底面棱边杆长度为m，当角度α取0°～90°之间任意角度时，六棱锥机构的完全收拢状态如图9所示，W表示视图方向，r表示空间六棱锥机构完全收拢后节点花盘的包络圆半径，R表示空间六棱锥机构完全收拢后的整体外端包络圆半径。

从图9中可以看出，空间六棱锥机构完全收拢后包络体积为

V=h×πR2=

h×π(r+msinα)2

(37)

式中：V表示包络体积。

图9 空间六棱锥机构完全收拢后包络体积Fig.9 Envelope volume of the fully folded space hexagonal pyramid mechanism

由式(37)可以看出，当机构杆件长度及节点花盘大小都已确定时，在0°～90°范围内，空间六棱锥机构完全收拢后的包络体积随着角度α的增大而增大。

当角度α取0°、90°以及其他任意角度时，六棱锥机构的完全收拢状态如图10所示，由图中可以看出，在节点花盘及构件长度都相同的情况下，角度α为0°时整体机构收缩后包络空间最小，收拢率最高，角度α为90°时整体机构收拢后包络空间最大，收拢率最低。

空间六棱锥机构完全展开状态如图11所示，图中红色箭头线为节点构件A和B的向心运动轨迹以及相对运动轨迹，同时从图中可以看出此机构完全展开状态时即为机构处于边界奇异位形的一个状态(即θ2=π/2)，如果此时沿竖直方向给机构施加一个作用力，机构在这一位置的传动角为0°，压力角为90°，机构的关节不能运动，六棱锥单元机构退化为自由度为0的结构，可依靠结构中的杆件自身抵消外力的作用，而在关节处不需要提供额外的驱动力矩，此时机构具有较好的结构刚度和力学性能。

图10 空间六棱锥机构完全收拢状态Fig.10 Fully folded states of space hexagonal pyramid mechanism

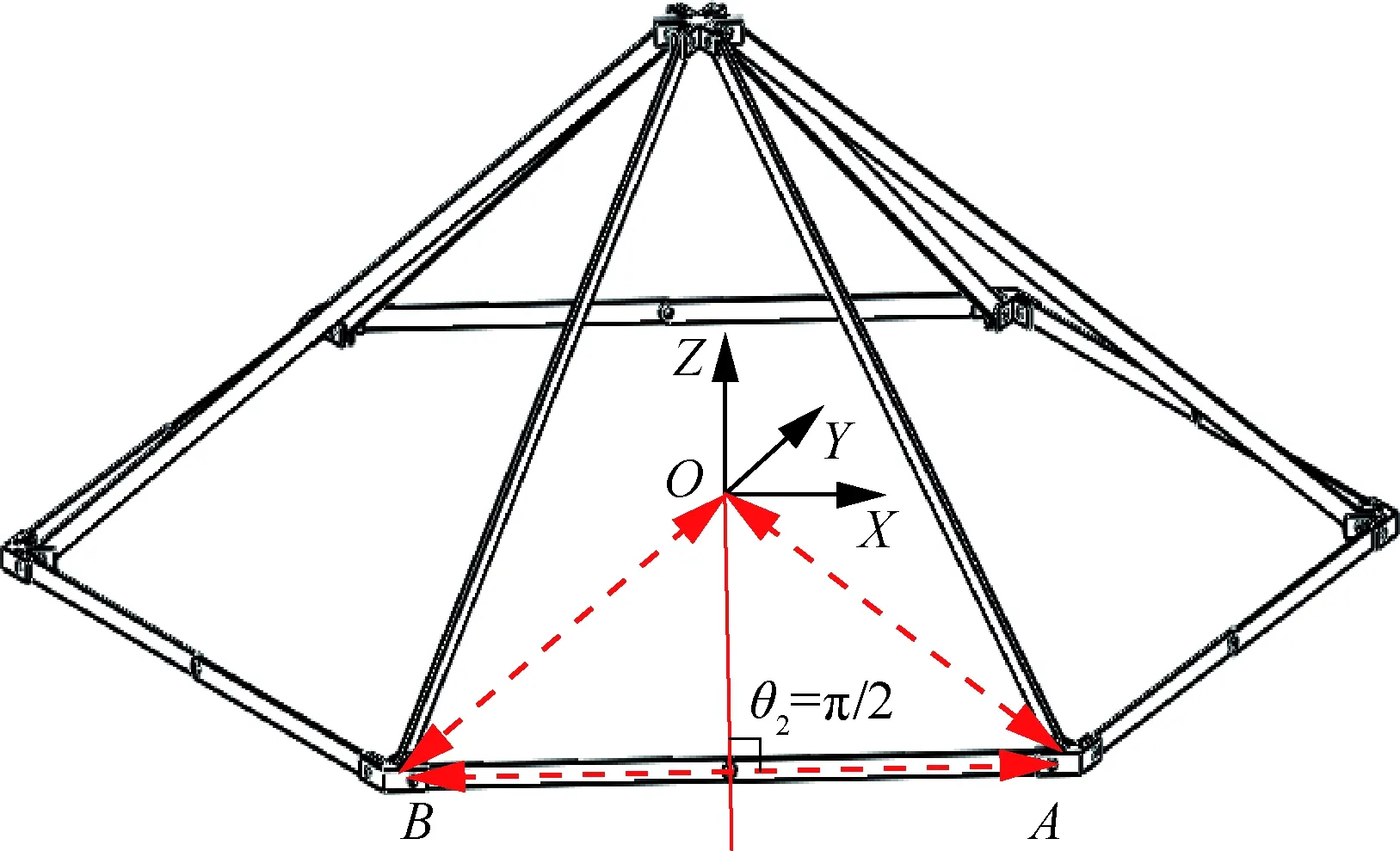
图11 空间六棱锥机构完全展开状态Fig.11 Fully deployed states of space hexagonal pyramid mechanism

综合以上分析，由不同数量的此空间对称型7R机构组合可以得到任意棱数的空间多棱锥机构，通过合理布置机构中运动副轴线方位可以使得多棱锥机构获得较大的收拢率，当机构完全展开时，由于其奇异特性，可以使之具有较好的力学性能，多个此类空间多棱锥机构可以扩展组合构造成为多种新型大尺度空间可展开机构，在航空航天领域具有较好的应用前景。

5 结 论

1) 针对一种空间对称型7R机构进行了分析，通过旋量拓扑图分析了其整体自由度，得到了其运动副轴线方位变化时整体机构自由度数目的变化图；基于反螺旋理论分析了运动副轴线方位不同的情况下运动输出构件的自由度数目和性质，并针对其瞬时性做了判别，发现其在不同运动副轴线方位布置情况下会出现局部自由度与瞬时自由度。

2) 将空间对称型7R机构等效为4R3P机构，根据其几何约束条件建立了机构运动约束方程组，分析了机构在不同驱动情况下的奇异特性，得到了机构在不同的驱动下处于奇异位形时的几何条件。

3) 通过合理布置运动副轴线方位，选定自由度为1且具有较大收拢率时的空间对称型7R机构单元组合构造了一类单自由度多棱锥型空间可展开机构，此类可展开机构处于完全展开状态时处于机构的一个奇异位形，可有效提高可展机构在工作状态时的静刚度和力学性能，同时通过多个棱锥型空间可展开机构的组合，可以构造出新型大尺度空间可展开机构，在航空航天领域具有重要的应用价值。