一种C波段大功率电调滤波器设计

魏 强,李晓东，王 彬, 蒋廷利，周 雨，邱海莲

(1.中国电子科技集团公司第二十六研究所, 重庆 400060；2. 西南大学 电子工程系，重庆 400715；3.云南省机电一体化应用技术重点实验室 云南省先进制造技术研究中心，云南 昆明 650031)

0 引言

现代武器系统面临的电磁环境日趋拥挤、异常复杂，频率捷变是电子抗干扰最主要的技术手段，电调滤波器是实现抗干扰微波系统的重要部件[1-2]。

综合文献[3-4]分析，对于U/V、L频段的电调滤波器报道较多，而对于C波段和更高频段的电调滤波器报道较少。

目前电调滤波器设计存在的难点有：

1) 滤波器失谐问题[5-7]。如何解决滤波器相对带宽随频率变化而发生显著变化的问题。

2) 伺服机构控制精度问题[8]。如何解决运动机构微行程、高精度、重复性的问题。

在工程应用中，还需解决温度、振动冲击等多种因素造成的频率漂移、误差问题。

本文介绍了一种恒定带宽耦合机构和运动执行机构的设计方法，并在此基础上完成了一款大功率C波段电调滤波器的研制，实测结果和理论仿真吻合，满足工程所需。

1 电调滤波器设计

电调滤波器的频率为4 400～5 000 MHz，带宽≥40 MHz，插入损耗≤1 dB，(f0±100 MHz)(f0为中心频率)带外抑制≥50 dBc，承受功率≥400 W，调频步进为10 MHz。高带外抑制和大功率是本滤波器的设计难点。

C波段电调滤波器有波导、同轴腔、钇铁石榴石(YIG)磁调3种实现方式[9]。YIG磁调滤波器性能优良，但其耐功率低。

技术指标要求调谐频率为4 400～5 000 MHz，对应波长变化0.82 mm。若采用λ/4(λ为自由空间波长)同轴腔，调谐行程为0.2 mm。若采用BJ48波导谐振腔，通过调谐销钉从波导H面插入，仿真计算，采用直径为∅10 mm的调谐销钉，其调谐行程为27 mm，可覆盖的频率为4.3～5.1 GHz。与同轴腔方案相比，从调谐精度上看，波导的调谐行程较长，调谐精度低，易工程实现。

此外，波导滤波器的峰值功率容量(介质为空气)为

(1)

式中：a、b分别为矩形波导截面长和宽；E为空气击穿电场强度。由式(1)可估算BJ48波导谐振腔的最大功率容量为467 kW，远大于相同尺寸同轴腔的承受功率。

采用KQ变换法[10]，四阶切比雪夫滤波器低通原型参数为g0=0.712 8，g1=1.200 3，g2=1.321 2，g3=0.647 6，g4=1.100 7。通过网络变换，实现此滤波器的拓扑结构如图1所示。

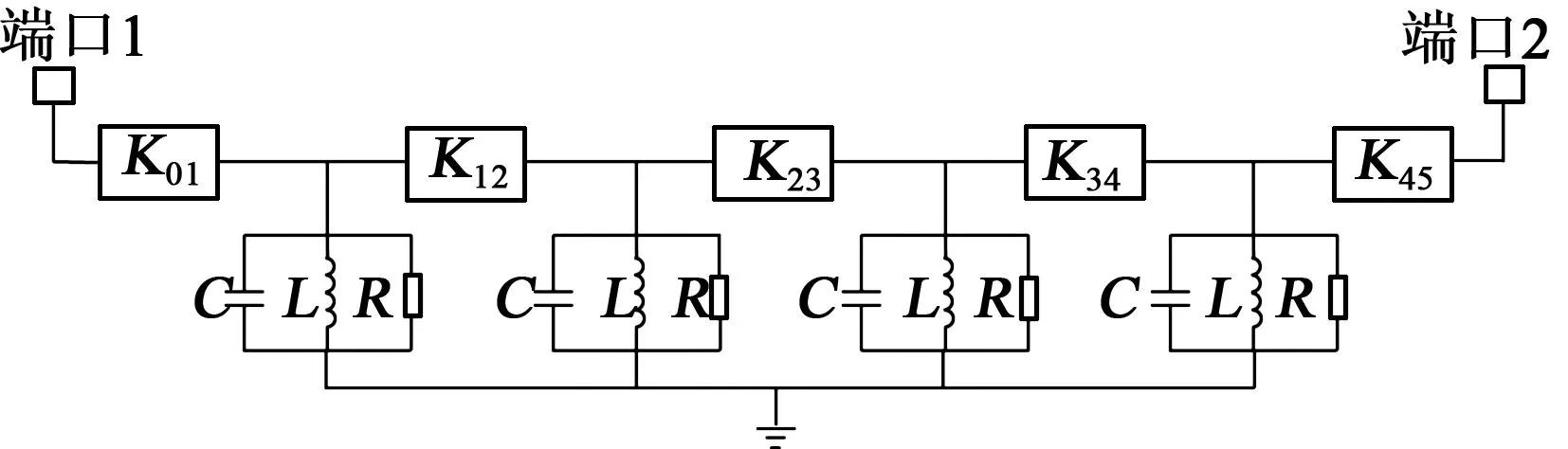
图1 滤波器网络拓扑结构原理图

图1中,各个腔间耦合系数Kij、谐振回路中的电感L、电容C、电阻R分别为

(2)

(3)

(4)

式中：BW为滤波器的绝对带宽;Q0为谐振回路的品质因数。采用从图1求出的耦合系数Kij作为耦合结构仿真理论值。

1.1 腔间耦合结构设计

由式(2)可见，当腔间耦合系数Kij为定值时，随着频率的升高，BW也应增大。理想的电调滤波器需要设计一种耦合结构，在整个调谐频率范围内，保持BW为定值的条件下，使Kij与中心频率f0的变化成反比，即要求Kij随f0的升高而降低，才能达到带宽恒定的目标。

物理结构耦合系数Ksim可以利用本征值计算公式求得，即

(5)

式中f1、f2为软件求得的2个本征模频率值。

定义Kij与Ksim之差的绝对值为ΔK，则有

ΔK=|Kij-Ksim|

(6)

通过给定的恒定滤波器带宽BW来确定Kij为频率的函数，即Kij(f)，并以式(6)作为目标函数，寻找合适的物理耦合结构，使ΔK恒趋近于0，解决失谐问题。

E面金属膜片滤波器是由在矩形波导宽边插入与E面平行的金属膜片和矩形波导共同构成，金属膜片起耦合作用，相邻膜片间构成谐振腔。通过改变这些金属膜片高度或宽度，实现集总元件(电容或电感)，图2为在矩形波导中插入电容、电感膜片的物理结构及其等效电路。图中，δ为膜片的厚度,B为电导，Y0为输出导纳。

图2 波导滤波器电容、电感等效耦合结构

传统E面波导滤波器耦合结构通常只采用单一的电感或电容膜片，膜片厚度、位置偏置结构参数与滤波器的中心频率、通带带宽有密切的联系[11]，不能够实现宽范围调谐。

通过分析E面波导滤波器耦合理论和仿真计算，最终选定的腔间耦合结构如图3所示，这种耦合结构由全高电感膜片和半高电容膜片共同构成，满足式(6)要求，确定耦合结构尺寸的初值。

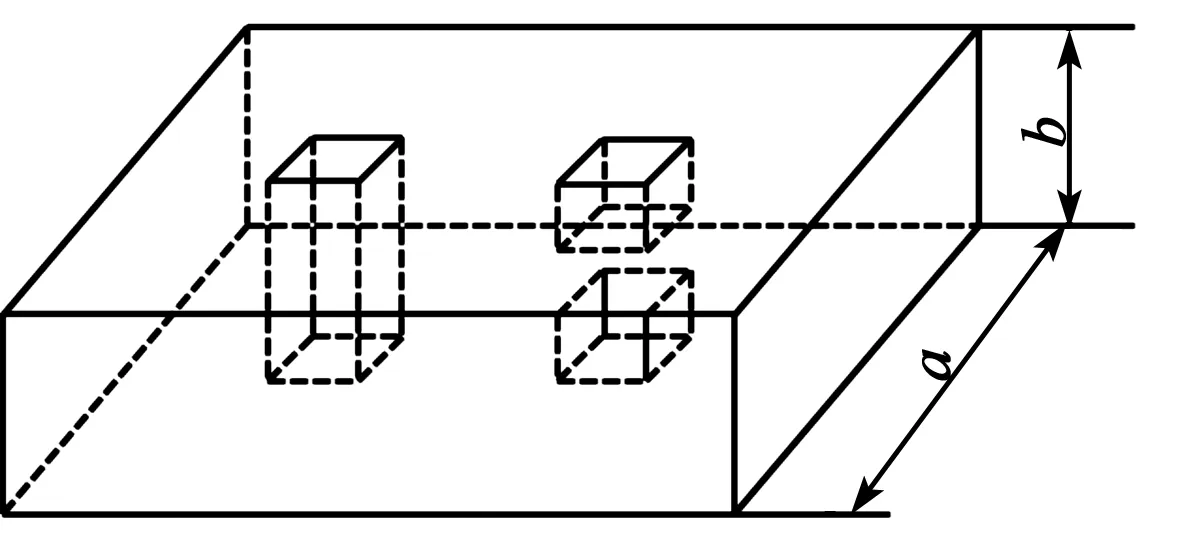
图3 恒定带宽混合耦合结构

1.2 滤波器设计

滤波器由耦合结构和谐振腔级联而成, 如图4所示。

图4 波导滤波器结构剖分

将滤波器拆分为耦合结构参数仿真、谐振器长度仿真、滤波器整体仿真3个步骤。

1) 耦合结构参数仿真。按照图3所示结构建模, 仿真其在中心频率4.7 GHz处的传输系数S12值，直到其S12的仿真结果与理论数据相符, 求出耦合结构的初值。

2) 谐振器腔体长度仿真。根据耦合结构的尺寸建立谐振器模型, 调整谐振器的长度，使单腔谐振器的谐振频率与所要求的滤波器通带中心频率一致, 即可以算出谐振器的长度。

3) 滤波器整体仿真。把所有的耦合结构和谐振器结构交替级联起来(见图5)，利用场路结合、协同仿真[12]的方法, 对滤波器进行整体仿真优化, 完成滤波器设计。

图5 波导滤波器协同仿真

图6为波导滤波器仿真频响。仿真优化结果表明，在4.4 GHz、4.7 GHz、5 GHz 3个频点，带宽分别为47 MHz、43 MHz、45 MHz，偏离中心频率100 MHz，抑制度分别为55 dB、65 dB、65 dB，在整个调谐频段内带宽变化≤5 MHz，驻波、抑制等指标满足要求。

图6 波导滤波器仿真频响

2 执行机构软硬件设计

2.1 执行机构硬件设计

为满足设计指标，要求电调滤波器伺服机构位置控制灵活，响应快，定位准确。直流伺服系统存在维护费高,堵转易烧毁及控制复杂等问题。交流伺服系统维护性低，控制技术成熟，但成本较高。步进电机伺服系统有可靠性高、性价比高、便于计算机控制等优点。因此，采用步进电机作为执行机构硬件首选。

通过理论仿真，得到调谐螺钉行程和频率关系，即频率变化10 MHz，调谐活塞变化0.45 mm，且在调谐范围内，二者近似为线性关系。因此，除对运动部件的加工精度有较高要求外，还需合理设计执行机构才能满足要求。图7为执行机构运动控制系统硬件组成[13]。

图7 控制板硬件构成

主控单元通过UART数据接口向伺服控制系统单片机发送频率相关的配置信息，经过处理将频率值转化成步进电机运动参数，控制执行机构运动到相应位置，从而实现选频功能。驱动放大器驱动步进电机动作。机械限位开关限制内导体的运动范围，而光电开关确定内导体的运动零点位置。滤波器腔体和运动机构为机械结构件，性能的调整只能依靠存储的数据，而温度环境的变化会改变滤波器性能，因此，在运动控制系统中增加了温度补偿，使温度变化引起的频漂得到抑制，提高了系统的精度，也增加了系统的环境适应性。主控单元实物如图8所示。

图8 控制板实物

运动机构零点决定了整个滤波器的控制精度。零点的确定采用了初零、细零和步进电机机械零点三级控制方法，实现了执行机构运动零点的唯一性，提高了滤波器的准确度。当调谐杆经过机械零点时，零点位置触发电路将输出脉冲信号，处理器接收到该脉冲信号，然后从该机械零点开始计数，直到调谐杆运动到指定步数，电机停止，调谐完成。从零点位置开始到指定位置，要经3个阶段：

1) 低速寻找零点。寻找机械零点时，电机转速低，寻找起始位置零点。

2) 恒定速度运行。为提高系统响应速度，必须在较短时间内运动到指定位置，所以，从零点开始加速到最高速度后，以最高速度运行一定距离。

3) 以低速运动到指定位置。当调谐杆运动至指定位置前必须减速，以防过冲，降低控制精度。

2.2 执行机构软件设计

运动控制系统的控制策略和控制方法都是通过软件实现的，要达到理想的运动控制效果，控制软件的设计至关重要。滤波器控制软件由初始化函数、运动函数、复位函数组成，程序框图如图9所示[13]。

图9 滤波器控制软件流程框图

当系统上电复位后，对系统各部分进行初始化，然后等待上位机发送调谐指令。当接收到一条完整的调谐指令后，根据协议计算出频点，如果频点在规定范围内，读取存储器中该频点所对应的步数。存储器中只存放了频点为整数兆赫兹所对应的步数，当频点为非整数兆赫兹时，采用线性插值算法，根据前、后频点的步数计算出频点所对应的步数。当电机运动结束，调谐完成，等待下一次调谐指令。

3 实验结果

根据上述设计思路, 对电调滤波器进行了实物加工, 使用Agilent E5071C网络分析仪进行测试。在室温25 ℃下实测结果如图10所示，3组曲线分别对应f0为4 400 MHz、4 700 MHz、5 000 MHz时的频响、驻波特性。在整个调谐过程中，3 dB带宽≥40 MHz，插损≤0.6 dB，驻波≤1.5。

图10 滤波器实测频响

由图10可知，在整个调谐范围内，滤波器的响应形状和相对带宽保持不变，较好地满足了工程实际需要。

4 结束语

本文研制的电调滤波器具有恒定带宽、承受功率大的特点，在系统应用中性能稳定，已批量生产。通过滤波器和伺服传动机构的机电一体化设计，研制结构更紧凑的大功率电调滤波器满足通信设备高集成、小型化的要求，具有广阔的应用前景。