小型磁悬浮CMG高速转子动框架效应前馈补偿与实验*
吕奇超,吕东元,李延宝,刘平凡
(1.上海航天控制技术研究所·上海·201109;2.上海市空间智能控制技术重点实验室·上海·201109;3.清华大学·北京·100084)
0 引 言
控制力矩陀螺(Control Moment Gyroscope,CMG)是大型航天器完成姿态控制与快速机动必不可少的关键单机。它主要由高速转子系统和框架系统组成,通过框架转动实现动量矩主轴的偏转,进而在垂直角动量方向产生相应的陀螺控制力矩[1]。其中,CMG高速转子的支承方式是决定CMG性能的最主要因素之一[2]。对于采用机械支承的CMG高速转子而言,磨损和振动不仅影响着CMG的精度和寿命,其对平台姿控精度和稳定度的影响也尤为显著。为适应大型卫星平台姿态控制对高精度、长寿命CMG的迫切需求,北京航空航天大学、国防科技大学等开展了磁悬浮控制力矩陀螺关键技术的攻关和样机的研制[3-8],利用磁悬浮转子与定子无接触的优点,实现了执行机构的长寿命、低摩擦及极低振动[4]。针对航天器对磁浮控制力矩陀螺体积小、质量小、低功耗、较大输出力矩等方面的应用要求,上海航天控制技术研究所研制了功能密度更高的75Nms小型单框架磁悬浮控制力矩陀螺,磁悬浮高速转子的最高转速为30000r/min,本体质量≤18kg。
与刚性机械支承不同的是,磁悬浮支承实际上是具备一定刚度和阻尼的主动控制弹性支承。由于动框架效应[9],飞轮转子与定子之间会产生附加的相对运动,这将导致转子位移的跳动量显著增大;框架转动输出陀螺力矩并将其反作用于飞轮转子,会导致磁轴承的径向载荷和控制电流发生改变。这种动框架位移可能导致转子直接碰撞保护轴承,进而失稳。
为抑制力矩陀螺框架运动对磁浮转子的影响,文献[8-9]在磁轴承控制中引入了基于框架角速率的固定特性前馈校正,其补偿效果取决于模型的精度。文献[10]基于非线性模型,提出了基于实测频率响应的优化加速度前馈校正算法。文献[2]和文献[11]研究了基于X-滤波最小均方算法的自适应前馈技术,降低了对模型误差的影响;但是,由于磁轴承的控制算法复杂、带宽响应高,复杂的动框架抑制技术难以实现工程应用。
本文在分析磁悬浮力矩陀螺高速磁浮转子受力特性的基础上,针对所研制的75Nms立式小型单框架磁悬浮控制力矩陀螺的高速内转子,采用角速率前馈控制策略实现了磁轴承控制器对动框架效应引发的力矩扰动的有效抑制,并在此基础上进行了整机输出特性测试。
1 CMG高速转子的建模与分析
小型单框架磁悬浮控制力矩陀螺(如图1(a)所示),由磁悬浮高速飞轮转子(内转子)、支撑内转子的框架,以及框架伺服系统及其支承结构等组成。当框架转动时,强制转子角动量方向将发生改变,并向外输出陀螺控制力矩。简化飞轮转子的受力情况如图1(b)所示。施加在转子上的力包括右径向磁轴承MB1、左径向磁轴承MB2,以及轴向磁轴承MB3的电磁力。O表示转子质心所在的位置。通过结构配重和安装,可以保证内转子质心过框架旋转轴,因此可简化转子坐标系与框架坐标系的关系,假定框架旋转轴与内转子x坐标轴重合。

(a)整体结构
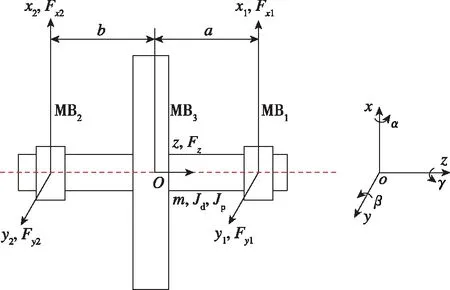
(b)受力模型与坐标定义图1 磁悬浮力矩陀螺结构(a)和高速转子受力模型(b)Fig.1 The integrated structure of the small magnetically suspended CMG (a) and the stressing model of the high speed rotor (b)
将磁悬浮控制力矩陀螺基座固连于地面(近似于惯性系),当框架以角速率ωg转动时,磁悬浮高速转子系统的动力学模型如式(1)所示。
(1)
式(1)中:xc、yc分别为磁悬浮高速转子质心的坐标,g为重力加速度,Ω为磁悬浮高速转子绕z轴转动的角速度,x1、y1为MB1处的坐标,x2、y2为MB2处的坐标,x、y、z为质心O处的坐标,α、β为转子绕x轴、y轴的转角,m、Jd、Jp为高速转子的质量、赤道转动惯量和极转动惯量,fx、fy、fz为磁轴承在x、y、z方向上的受力,px、py为磁轴承在x、y方向上的力矩。
式(1)可写为如下形式
(2)

Mout=JpΩωg
(3)
此时,在图1所示的转子坐标系下,通过对飞轮转子的受力进行分析可知,转子受力只在径向磁轴承x轴方向处有变化,在保证重力平衡的情况下,产生y轴方向的力矩
mg=Fx1+Fx2
(4)
Min=aFx1-bFx2
(5)
在式(4)、式(5)中,Fx1、Fx2分别为磁悬浮转子右端磁轴承、左端磁轴承在x轴方向上的受力,a、b分别为右端磁轴承、左端磁轴承与质心的距离。
由动量矩守恒原理可知
Min=-Mout=aFx1-bFx2=-JpΩωg
(6)
由式(3)~式(6)可知,在稳态下,CMG的输出力矩与其高速转子的角动量JpΩ、框架角速度ωg成正比。由上述分析可知,框架转动强制转子改变角动量方向产生作用于飞轮转子的陀螺力矩,会造成转子位移跳动量显著增大,不仅可能引发磁轴承受力饱和、导致转子直接碰撞保护轴承而失稳,而且还会给框架伺服系统带来振动,降低其相应速度和控制精度。
2 角速率-电流前馈控制算法
磁轴承的状态包括转子位移、磁轴承电流的状态两个方面,而轴承力是二者的函数。由上述分析可知,动框架效应是磁浮转子系统与框架之间动力学耦合的结果,极大地影响了磁轴承的悬浮稳定性;但就磁浮转子系统而言,如果忽略框架系统自身的动态过程和磁浮转子对框架系统的反作用,动框架扰动可简化为单向的运动约束和外部扰动。同时,由于框架运动是可测的,用前馈控制方法对其加以补偿,不仅具有无超调、无过渡过程和无差的优点[9],而且对原有闭环系统的影响较小,更有利于实际应用。
考虑到框架角加速度通常较小,由动框架效应造成的附加扰动力矩主要取决于框架的角速率,因而需要在磁轴承控制器中引入基于框架角速率的前馈补偿控制。加入前馈补偿环节后的径向磁轴承系统的控制框图如图2所示,图中,Gf(s)为前馈补偿传递函数矩阵,D(s)为等效振动力矩fg相对框架转速的传递函数矩阵。欲对扰动力矩进行完全补偿,Gf(s)需满足
(7)
式中,Gf(s)为前馈传递矩阵,由式(7)可得
(8)
在图2中,Gd(s)、Gc(s)分别为分散PID控制器和交叉反馈控制器传递函数矩阵。由于电涡流位移传感器、AD、DA和功放等的时间常数短,可将其视作比例环节,Ks、Kad、Kda、Kamp分别为传感器、AD、DA和功放的增益常数,Ki、Kx分别为电流刚度和负位移刚度,Tm和Ts分别为坐标转换矩阵。

图2 加入前馈校正环节的磁悬浮飞轮系统的结构框图Fig.2 The structural block diagram of the magnetically suspended flywheel system with the feed-forward compensation
由式(8)可知,前馈补偿传递函数矩阵Gf(s)与系统模型参数有关,模型参数的准确性将影响前馈补偿的效果。特别地,磁轴承各通道电流刚度Ki的真实值与理论值差别可能较大。此外,框架角速率信号的低通滤波和测量精度,也会影响动框架效应前馈校正的效果。
3 整机输出特性研究
3.1 框架运动对内转子轴心轨迹的影响
将磁悬浮高速飞轮转子升速至额定转速500Hz,并使其保持恒速稳定运行。控制外框架以不同角速率逆时针转动,研究框架运动对高速内框架的影响特性。
图3所示为当外框架电机以0(°)/s和1.5(°)/s的转速逆时针旋转时,飞轮转子上、下轴心的轨迹。图4所示为当外框架电机分别以0(°)/s和1.5(°)/s的转速逆时针旋转时,上径向磁轴承x方向和y方向的径向磁轴承电流。

(a)外框转速为0(°)/s时的轴心轨迹(a) The axle center trajectory with the speed of outer gimbals of 0(°)/s

(b)外框转速为1.5(°)/s时的轴心轨迹(b) The axle center trajectory with the speed of outer gimbals of 1.5(°)/s图3 飞轮内转子转速为500Hz时的轴心轨迹Fig.3 The axle center trajectory of the flywheel inner rotor at 500Hz
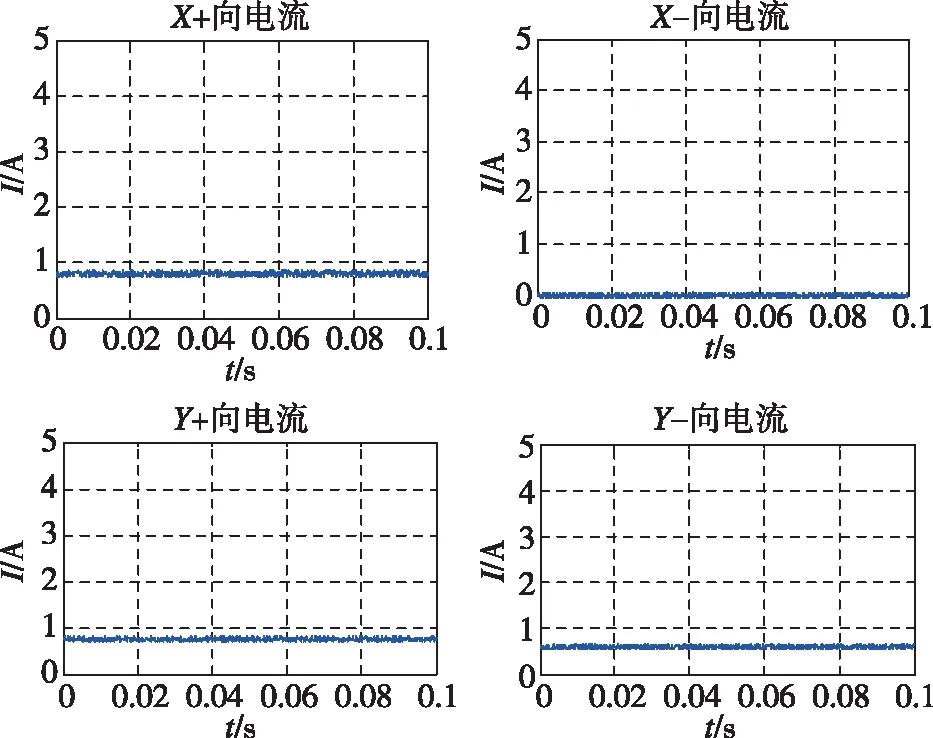
(a)外框转速为0(°)/s时的磁轴承电流(a) The current of magnetic bearings with the speed of outer gimbals of 0(°)/s
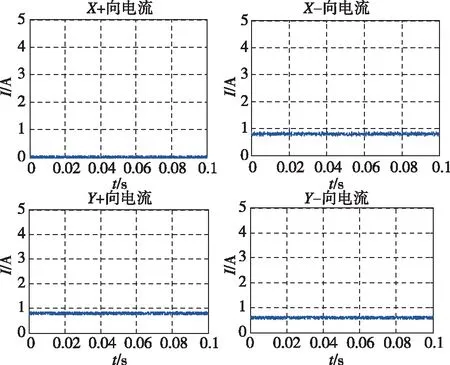
(b)外框转速为1.5(°)/s时的磁轴承电流(b) The current of magnetic bearings with the speed of outer gimbals of 1.5(°)/s图4 飞轮内转子转速为500Hz时的磁轴承电流Fig.4 The current of magnetic bearings of the flywheel inner rotor at 500Hz
对比图3和图4可知,随着外框架旋转速度的增加,磁悬浮高速内转子的轴心轨迹基本没有受到影响,磁轴承控制器动框架影响的补偿效果良好、鲁棒性好;同时,磁轴承控制电流是随着框架转速的增大而有较明显的变化的,反映出了控制力矩陀螺在输出力矩时对磁浮内转子受力状态的影响。
3.2 框架对磁轴承电流的影响
将磁悬浮高速飞轮内转子升速至一定转速,并使其保持稳定运行,控制外框架以不同转动角速度逆时针转动,记录径向磁轴承在各个方向上的电流。由于y方向电流变化很小,下文仅仅针对x方向的电流进行研究。
图5所示为高速飞轮内转子升速至100Hz、外框架以不同转速逆时针旋转时,径向磁轴承在x方向上的控制电流。

图5 当飞轮内转子转速为100Hz时、在不同外框架转速 下,下径向磁轴承在x方向上的控制电流Fig.5 The x control current of the lower radial magnetically bearings of the flywheel inner rotor at 100Hz varying from different speeds of the outer gimbals
图6所示为磁悬浮高速飞轮内转子升速至200Hz、外框架以不同转速逆时针旋转时,径向磁轴承在x方向上的控制电流。
由图5和图6可知,磁轴承控制电流是随着磁悬浮高速飞轮转子转速和外框架转速变化而变化的。由式(6)可知,飞轮输出力矩正比于飞轮转速和外框架转速的乘积,正比于径向磁轴承支承反作用力之差(a=b),且磁轴承支承反作用力正比于电流的平方。因此,磁轴承最大的承载力直接决定了飞轮的最大输出力矩。
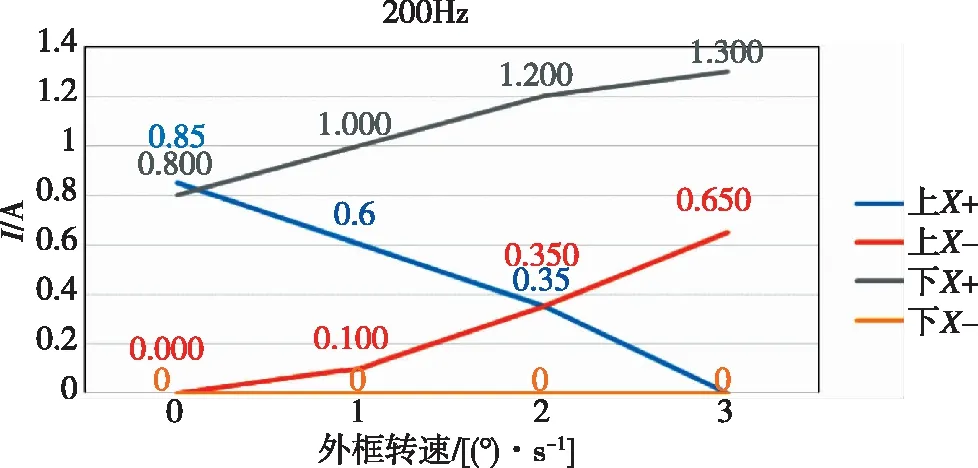
图6 当飞轮内转子转速为200Hz时、在不同外框架转速下, 下径向磁轴承在x方向上的控制电流Fig.6 The x control current of the lower radial magnetically bearings of the flywheel inner rotor at 200Hz varying from different speeds of the outer gimbals
3.3 整机力矩输出测试
将磁浮高速飞轮内转子升速至不同转速,并使其保持稳定运行,控制外框架转动直至磁悬浮高速飞轮转子轴心晃动,将此刻的转速记录为外框架的最大转速。此时,磁悬浮控制力矩陀螺的输出力矩可由式(6)计算而得,如表1所示。其中,极转动惯量为0.027kgm2,比设计指标略大。

表1 磁悬浮控制力矩陀螺在不同外框架转速下的 最大输出力矩Tab.1 The maximum output moment of the magnetically suspended CMG at different speeds of the outer gimbals
由表1所示,磁悬浮控制力矩陀螺在不同高速转子运行速度下的最大输出力矩因控制参数不同而略有差异,但是当由整机控制力矩输出时,内转子运行稳定,显示出其所采用的算法对动框架位移的较好的抑制作用。
4 结 论
针对75Nms小型磁悬浮控制力矩陀螺在力矩输出时动框架效应对其的影响,在分析了力矩陀螺高速转子受力特性的基础上,引入了基于框架角速率的前馈补偿策略,实现了对动框架扰动的有效抑制。试验结果表明,补偿后的系统能实现高速转子在全转速范围内的稳定运行,提高了飞轮转子在框架运动时的响应速度,有效降低了转子位移的跳动量,达到了对动框架效应的有效抑制。
框架转动输出陀螺力矩反作用于飞轮转子,会导致磁轴承径向载荷和控制电流发生改变,易引发磁轴承受力饱和。论文后续还将针对磁轴承结构优化及提高整机力矩输出能力,开展进一步的研究。

