基于拉盖尔函数的卫星姿态预测控制方法*

胡庆雷，解静洁，奚 勇

(1. 北京航空航天大学 自动化科学与电气工程学院·北京·100191；2.上海航天控制技术研究所·上海·201109)

0 引 言

航天器的在轨服务与维修技术已成为各个国家航天工程的重要任务，也是在深空探测中必不可少的重点工程项目之一。随着空间环境的日益复杂化，未来空间任务对自主卫星的安全性、有效性及快速性均提出了更高的要求[1]。由于空间环境复杂多变，卫星在对空间站进行巡视侦查的过程中，姿态的指向会受到太阳等的影响，使得敏感仪器发生故障甚至造成损坏，从而导致卫星系统不稳定，使得空间任务失败[2]。同时，卫星会受到自身物理性能的影响，如控制力矩及运行状态的限制。因此，研究卫星在复杂空间环境中的禁飞区域及在自身性能约束条件下的姿态控制问题，是航天任务中的前沿基础，设计新型有效的卫星姿态控制算法具有重要的工程实际意义。

近年来，国内外学者已经在卫星姿态的控制与研究领域取得了非常多的研究成果，然而在这些姿态控制方法中，存在着许多尚未解决与突破的问题。例如:文献[3]采用了滑模PID方法实现了卫星的姿态控制，但该方法无法处理多种约束，无法实现能量最优的要求；文献[4]提出了一种基于变结构控制的卫星姿态控制方法，然而该方法存在着抖振问题；文献[5]采用了势函数的控制方法，但是该方法存在着局部最小值的问题；文献[6]采用了反步法对卫星的姿态进行控制，而其对控制输入的求导会带来微分爆炸的问题。

模型预测控制(Model Predictive Control，MPC)是一种能够处理优化目标和约束的优化控制方法，并且不存在上述传统的姿态控制方法的问题，被广泛应用于姿态控制等任务中。最初的模型预测控制方法主要被用于工业领域，而现在已经被成功地应用在了其他领域中，如航天飞行器[7]、导弹[8]、无人机[9]等，并在控制优化问题中发挥了巨大的潜力。模型预测控制的主要核心思想是预测系统的未来输出值，将所得到的最优控制序列的第1个优化解作用于系统，依次滚动向前进行[10]。预测控制具有可在线处理约束的优点，为工程领域提供了一种高可靠性、高实用性、高稳定性的优化算法。

模型预测控制已被广泛应用于许多研究中，例如:文献[11]提出了一种以分段放射模型实现预测控制的方法，以解决航天器在着陆过程中的姿态约束问题；文献[12]提出了一种显示的模型预测控制方法，以解决卫星的姿态控制问题，采用多参数二次规划方法进行求解；文献[13]提出了一种基于遗传算法的卫星姿态机动的模型预测控制方法。然而，这些文献中的模型预测控制计算量大，计算效率低，对于复杂的问题可执行性较差，其理论研究与实际应用很难达到一定的水平，对于模型预测控制方法的稳定性证明还缺乏严格完备的理论支撑。

针对以上文献中的问题，本文提出了一种基于拉盖尔函数的模型预测控制方法，以解决卫星在空间站中的姿态控制问题。通过拉盖尔函数，可将传统方法中众多的控制序列转化为个数很少的拉盖尔参数，降低了优化求解过程中的计算维度，避免了传统模型预测控制器计算的复杂性，减少了计算量[14]。近些年，拉盖尔模型预测控制受到了国内外学者的广泛关注，如文献[7]对航天器的近距离操作提出了一种显示的拉盖尔模型预测控制方法，避免了计算爆炸的问题。据此，本文主要任务为在卫星在空间站中进行检测侦查的任务下，在绕飞的过程中，使卫星的姿态视轴指向空间站的实验舱及核心舱，并能够躲避禁止区域，避免卫星指向太阳而造成敏感仪器的损坏。通过采用拉盖尔模型预测控制方法，解决该卫星在禁止区域中的姿态约束问题，并能够使卫星指向指定位置。

本文的其余部分安排如下：第1部分制定了卫星的姿态控制问题；第2部分提出了基于拉盖尔函数的模型预测控制方法，求解了卫星的姿态控制问题；第3部分给出了相应的数值仿真结果；第4部分得出了结论。

1 卫星的姿态控制问题

考虑卫星在空间站进行绕飞检测时，卫星的姿态轴需指向指定位置，并且需要避免指向太阳，躲避禁飞区域，其姿态控制模型如图1所示，现根据该模型建立卫星的姿态控制方案。

图1 卫星在空间站中的姿态控制模型Fig.1 Attitude control model of satellite in space station

首先，卫星姿态的运动学和动力学模型可以表示为[15]

(1)

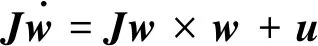
(2)

将卫星姿态的运动学和动力学模型写成状态方程形式，则有

(3)

其中，状态向量

考虑卫星自身的性能约束，其控制力矩约束和角速度约束分别为

|u|≤umax

(4)

|w|≤wmax

(5)

其中，umax和wmax分别为卫星控制力矩和角速度的最大值。

卫星在空间站绕飞过程中受到禁止区的限制，其姿态指向必须绕过禁止区，以避免卫星的敏感仪器经过太阳等的光照而受到损坏或精度降低。图2给出了卫星的锥形禁止区示意图。其中，yf为禁止区的约束轴，θf为禁止区域的角度，xf为卫星的期望指向，满足约束

xf·yf≤cosθf

(6)

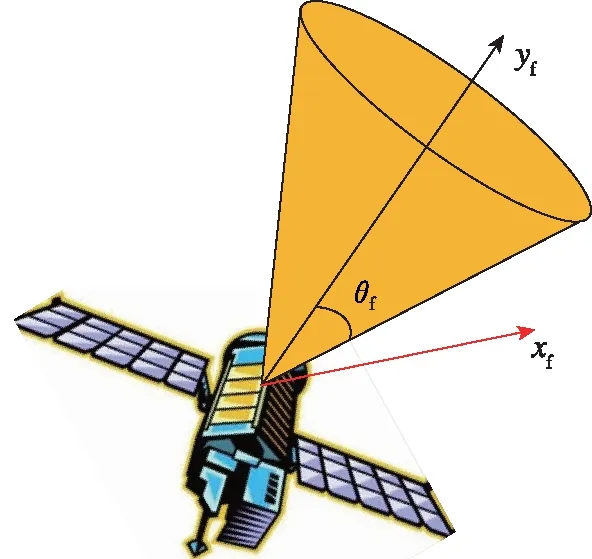
图2 卫星姿态的禁止区约束Fig.2 Forbidden zone constraint of satellite attitude

根据参考文献[16]可将上述约束简化为

qTMfq≤0

(7)

(8)

卫星姿态控制的优化目标为到达指定姿态及最小化控制力矩，故可表示为

(9)

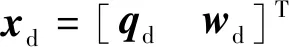
给定卫星的运动学和动力学模型，以及卫星的性能约束和姿态约束后，根据所制定的优化目标，卫星的姿态控制问题可表示为如下的优化问题

(10)

(11)

(12)

qTMfq≤0

(13)

|u|≤umax

(14)

|w|≤wmax

(15)

x(t0)=x0,x(tf)=xd,w(t0)=w0,w(tf)=wd

(16)

其中，x0，w0分别为卫星的初始状态和初始角速度，wd为卫星的期望角速度。

2 基于拉盖尔函数的模型预测控制

xk+i+1/k=Akxk+i/k+Bkuk+i/ki=0,…,Np

(17)

xk+i/k∈Xi=0,…,Np
uk+i/k∈Ui=0,…,Np
xk+Np/k∈X

(18)

其中，Np是预测窗，xk+i/k是当前k时刻第i步的预测值，uk+i/k为当前k时刻第i步的控制输入预测值，X是状态约束集，U是输入约束集，xk+Np/k是终端状态量，满足终端约束集：xk+Np/k∈{vk+Np/k=0}。

为了便于模型预测控制的实施，需要将卫星姿态模型进行离散化处理

x(k+i+1/k)=Akx0+Bku(k+i/k)
i=0,…,Np-1

(19)

其中x0为初始状态，Ak和Bk可以写为

(20)

其中Ts为采样周期。

在模型预测控制中，由于控制序列在每个优化预测窗内存在很多参数，求解效率降低，因此一种基于拉盖尔函数的模型预测控制可以减少优化序列，从而提高计算效率。该方法将所有预测窗内的优化序列通过拉盖尔函数转换为较少的优化序列。首先，原来的模型预测控制方法的控制序列为

(21)

其中，n表示控制输入的个数。通过拉盖尔函数，在当前采样时刻i下、第k步的控制输入可以表示为

u(k+i)=LT(i)η

(22)

其中，LT(i)是拉盖尔函数集，η为拉盖尔系数。对于第n个控制输入, 拉盖尔函数LnT(i)可以表示为一个向量形式

(23)

其中，Nn是扩展个数。拉盖尔函数满足正交性，即有

(24)

拉盖尔系数η为

(25)

对于第n个控制，拉盖尔系数ηn可表示为

(26)

拉盖尔函数集合满足下列的等式

L(i+1)=AlL(i)

(27)

(28)

其中Al是由参数α和β组成的转移矩阵，拉盖尔函数的初始值为

(29)

为了使系统稳定，参数α需要满足0≤α≤1[7]。通过拉盖尔函数的转换，控制输入uk/k,uk+1/k,…,uk+i/k(i=1,…,Np) 可以被少量的拉盖尔参数η所取代, 因此计算量可减少。当α=0、Nn=0时，拉盖尔函数的模型预测控制方法即为传统的模型预测控制方法。此时，由系统状态模型可以推导出由拉盖尔系数组成的表达式

(30)

即

(31)

上式可进一步写为

X=Fx(k)+Φη

(32)

其中，X=[xT(k+1|k)xT(k+2|k) …

xT(k+Np|k)]T，F=[AT(A2)T… (ANp)T]T，

(33)

其中，ηn是一个(N1+N2+N3)维的向量。

因此，目标函数为

xf)TQ(x(k+i|k)-xf)+ηTRη

(34)

基于上述拉盖尔函数，卫星的性能约束可转化为相应的表示形式。其中，控制力矩约束可以写为

-umaxIN≤L(i)η≤umaxIN∀i∈{0,…,Np-1}

(35)

角速度约束可以转换为

-wmaxIN≤Cwxk+i/k≤wmaxIN∀i∈{1,…,Np-1}

(36)

卫星的姿态禁止区约束为

(37)

值得注意的是，为了使计算可行，扩展项Nn应该小于预测窗Np的长度[7]。因此，通过使用拉盖尔函数，可减少预测控制输入的个数，从而减少计算量，故该姿态控制问题可表示为

minJ

(38)

Xk+i+1/k=AkXk+i/k+BkUk+i/ki=0,…,N-1

(39)

-umaxIN≤L(i)η≤umaxIN∀i∈{0,…,Np-1}

(40)

-wmaxIN≤Cxk+i/k≤wmaxIN∀i∈{1,…,Np-1}

(41)

(42)

(43)

3 仿真试验及结果分析

考虑卫星在空间站中绕飞以完成检测侦查空间任务，卫星需要对准空间站的实验舱及核心舱，以完成检测。首先，卫星在安全约束走廊中完成绕飞轨迹；其次，在某一轨迹点处调整自身姿态，使其视轴指向空间站的核心舱。在姿态控制过程中，需要避免其视轴指向禁止区域，即避免由对准太阳而造成的自身敏感仪器的损坏。

在仿真中，卫星的相关参数如表1所示。目标函数的权值矩阵分别为Q=0.1I7×7,R=0.1I3×3。

控制力矩的最大值为umax=100mN·m, 角速度的最大值为wmax=0.1rad/s。在基于拉盖尔函数的模型预测控制中，参数α=0.67, 扩展项为N1=N2=N3=3。

表1 卫星的仿真参数Tab.1 Simulation parameters of the satellite

仿真过程采用一种基于MATLAB的建模语言YALMIP进行模拟，依赖于外部求解器MOSEK。本文的数值仿真结果是在Windows / 64-X86平台上获得的，采用的优化软件为MOSEK7.1.0.12。仿真结果如图3所示。其中，蓝色实线为卫星绕飞空间站的轨迹，黑色曲线框是卫星轨迹的安全区域。黄色锥形区域即为卫星姿态控制的禁止区域，其中心轴指向太阳，红色直线指向是卫星的视轴方向，初始视轴方向指向x0处，期望视轴方向指向xd处，黑色曲线即为卫星姿态控制过程中的姿态转向轨迹。

图3 卫星姿态控制的轨迹图Fig.3 Trajectory of satellite attitude control

从图3可以看出，黑色轨迹线避开了禁止区域，表明了卫星在姿态控制过程中，其视轴指向能够从起始位置指向期望位置，并能够成功躲避禁止区域，避免了卫星视轴指向太阳而带来的损坏。为了进一步更加清晰地表现出卫星的姿态控制，将其视轴转向部分放大，结果如图4所示。

图4 卫星姿态控制的局部放大图Fig.4 Partial enlargement of satellite attitude control

在卫星的姿态控制过程中，卫星四元数的变化曲线如图5所示，角速度的变化如图6所示，卫星的姿态角变化如图7所示，图8为卫星姿态控制力矩的变化曲线图。

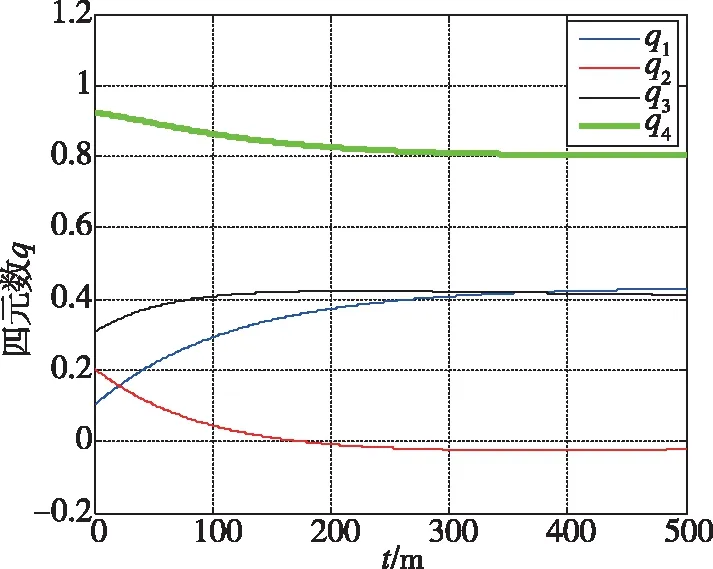
图5 卫星姿态四元数的变化曲线图Fig.5 The variation of satellite attitude quaternion

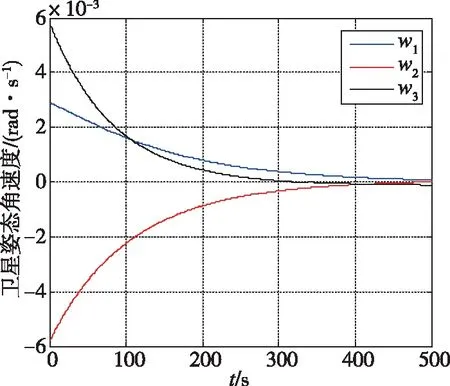
图6 卫星姿态角速度的变化曲线图Fig.6 The variation of satellite attitude angular velocity

图7 卫星姿态角的变化曲线图Fig.7 The variation of satellite attitude euler angle

图8 卫星姿态控制力矩的变化曲线图Fig.8 The variation of satellite attitude control torque

为了说明所提出的基于拉盖尔函数的模型预测控制方法能够提高优化效率及减少计算时间，采用了模型预测控制方法进行求解，表2给出了两种方法的优化求解器在每一步优化过程中的平均求解时间。由表2可知，基于拉盖尔函数的模型预测控制的平均每步优化时间较少，改善了模型预测控制方法的优化效率。

表2 两种方法的求解时间Tab.2 Solving time of two methods

4 结 论

本文研究了在空间站中进行绕飞检测的卫星的姿态控制问题，设计了一种基于拉盖尔函数的模型预测控制方法，解决了卫星在空间站中考虑禁飞区约束的姿态控制问题。针对卫星姿态轴在空间站中需躲避太阳等因素的影响，建立了禁飞区域约束；考虑卫星自身性能的约束，建立了控制力矩约束和角速度约束；为了使卫星姿态轴到达指定位置及在控制过程中能耗最优，建立了相应的目标函数；提出了用一种基于拉盖尔函数的模型预测控制方法进行求解，即通过拉盖尔函数，将多个控制输入转换为少数的拉盖尔系数，采用模型预测控制的优化策略进行优化。所提出的方法改善了传统的模型预测控制方法计算效率差的问题，减少了优化时间。通过使用卫星在空间站中绕飞的模型进行数值仿真验证，实验结果表明该方法能够使卫星的姿态轴躲避禁飞区并到达指定位置。与传统的方法相比，优化效率得到了显著提高。