螺杆转子的建模及模态分析

赵佳磊， 李志峰

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

干式双螺杆真空泵与其他类型真空泵相比具有结构紧凑、多相混输、动力平衡性好等优点，常用于食品、医疗、化工等领域[1]。其核心工作部件是一对相互啮合的阴、阳转子，阴、阳转子的性能直接影响着整个螺杆泵的工作情况。

国内外许多学者对阴、阳转子的型线进行了研究，HE Xue-ming等[2]应用NURBS曲线和流体动力学设计了不对称销圆弧齿型螺杆转子齿廓；施国江[3]利用NURBS从正反两面对转子型线进行了局部调整；黄海楠等[4]采用啮合线法结合龙贝格求积公式实现了对转子曲线的反向设计；费志强等[5]采用长幅内摆线和长幅外摆线组合曲线，基于包络法得到了螺杆的共轭齿形；吴高捷等[6]对螺杆转子的模态进行了分析，发现阳转子固有频率小于阴转子的固有频率。

综上所述，目前对阴、阳螺杆转子的研究多为二维端面型线设计计算，对三维建模及其模态分析介绍较少。本文从阴、阳转子端面型线计算到三维建模，对阴、阳螺杆转子前6阶模态分别进行了分析，并求得阴、阳转子正常工作时的激振频率，为保证转子正常运转提供参考。

1 螺杆转子二维型线计算及三维建模

双边对称圆弧型线的各段曲线主要由圆弧、摆线和点这3种性质的曲线构成。在设计转子型线时，需先给定阴转子或阳转子一段完整齿廓曲线，通过坐标变换可求得另一个转子曲线。螺杆转子的型线是指其端面的齿形，本文主要以双边对称圆弧型线的螺杆转子端面截形为例进行计算，由于该端面截形为对称曲线，故只需计算其中一对完整齿形即可。

1.1 二维坐标变换

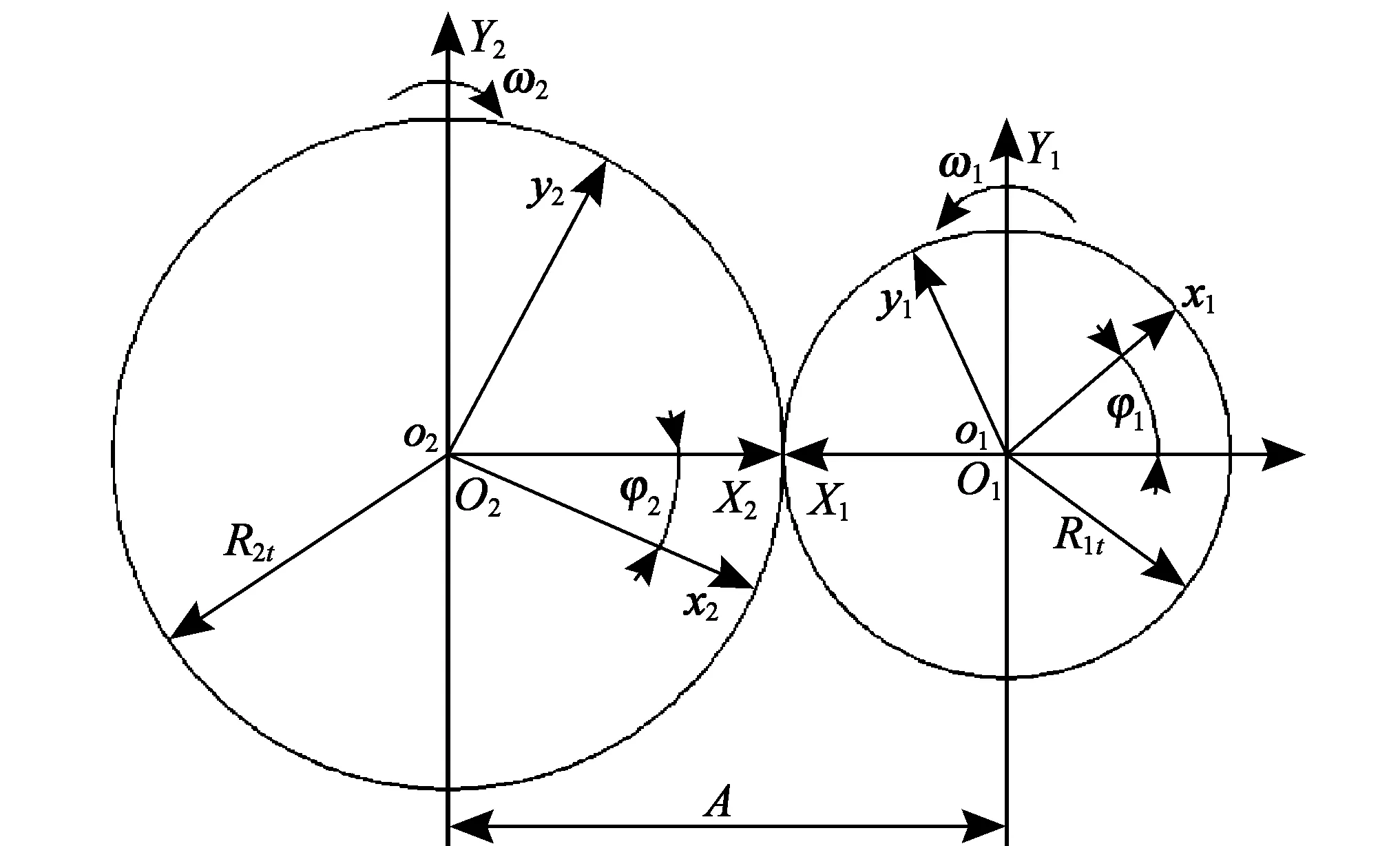
图1 坐标关系图

二维坐标变换是描述一种坐标系统变换到另一种坐标系统的过程，需要建立两个坐标系统之间的对应关系，其具体关系如图1所示。图中o1x1y1为固定在阳转子上的动坐标系，o2x2y2为固定在阴转子上的动坐标系，O1X1Y1为阳转子的静坐标系，O2X2Y2为阴转子的静坐标系，φ2、φ1为阴、阳转子转角，R2t、R1t为阴、阳转子节圆半径。

由图1所示的坐标关系图可知，动坐标系o1x1y1与动坐标系o2x2y2变换为

(1)

1.2 阴、阳转子的型线推导

将阴、阳转子一对完整齿廓啮合关系垂直投影到端面，可以推导各段曲线方程和其相应参数的变化范围。已知阳转子端面型线，使用坐标变换公式(1)可得到阴转子的端面型线，其推导过程如下。

①HI段与AB段：将HI代入动坐标变换(1)中可得AB段曲线，约束条件-β2≤β≤β1，则

(2)

(3)

②C点与IJ段：将C点代入动坐标变换(1)中可得IJ段曲线，即

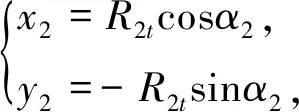
(4)

(5)

③I点与BC段：将I点代入动坐标变换(1)中可得BC段曲线，即

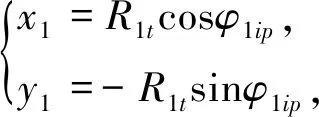
(6)

(7)

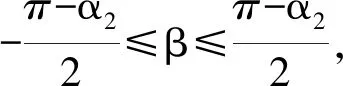
(8)

(9)

⑤D点和KL段：将D点代入动坐标变换(1)中可得KL段曲线，即

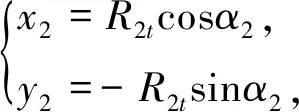
(10)

(11)

⑥L点和DE段：将L点代入动坐标变换(1)中可得DE段曲线，即

(12)

(13)

⑦LM段和EF段：LM、EF曲线分别和HI、AB关于x轴对称，约束范围为β1≤β≤β2，则

(14)

(15)

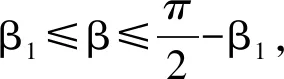
(16)

(17)

根据某厂双边对称圆弧型线的阴、阳转子参数，阴、阳转子齿数比i=4∶6，阳转子节圆半径R1t=52 mm，阴转子的节圆半径R2t=78 mm，中心距A=130 mm，阳转子齿底、阴转子齿顶小圆弧半径R0=5 mm，基圆半径R=31 mm。上述公式中α1、α2、β1、β2为过渡保护角，φ1i、φ1j分别为IJ、KL段的始、末过渡角，φ1b、φ1c分别为BC、DE段的始、末过渡角，φ1ip为I、L点过渡角。

通过MATLAB编程计算可得，阳转子齿形如图2所示，HI、JK、LM、MN为圆弧线段，IJ、KL为摆线；阴转子齿形如图3所示，AB、CD、EF、FG为圆弧线段，BC、DE为摆线，阴、阳转子各段曲线依次首尾光滑连接构成转子的一个完整齿形。

图2 阳转子齿形图 图3 阴转子齿形图

将MATLAB计算所得一系列离散的型线点，在UG中进行数据拟合，将一个完整齿形进行圆周阵列，得到阴、阳转子的截面型线，进行螺旋扫描拉伸得到阴、阳转子三维实体模型如图4。由文献[3]计算可得阳转子的螺距为448.2 mm，阴转子的螺距为298.8 mm，有效工作长度均为249 mm。

(a) 阴转子 (b) 阳转子图4 阴、阳转子三维实体

2 螺杆转子的理论分析

在对阴、阳转子进行模态分析时，需要考虑其实际工作状态下的固有频率、阻尼比和模态振型。阴、阳转子的固有频率只与自身的物理属性有关，如形状、材料和质量等，与外界其他条件无关[7-10]。在无阻尼系统中，其机械结构的动力学方程为

[M]{ü}+[K]{u}={0}，

(18)

式中[M]为质量矩阵，[K]为刚度矩阵，{ü}为节点加速度向量，{u}为节点位移向量。

线性系统的无阻尼自由振动可以用公式表示为

{u}={φi}cos(wit)，

(19)

其中{φi}表示第i阶模态形状的特征向量，wi表示第i阶自然振动频率，t表示时间。

由式(18)、(19)可最终求得

(20)

由(20)式可求得第i阶自然振动频率wi，进一步可求得第i阶模态的特征向量。

3 模态分析

3.1 材料设置及网格划分

将在UG软件中建好的阴、阳转子模型导入ANSYS软件中，设置阴、阳螺杆的材料为40Cr，密度ρ为7850 kg/m3，泊松比μ为0.3，弹性模量E为210 GPa。由于实际中螺杆轴上会有螺纹，轴端部有倒角，不利于网格划分，而且其对模态影响很小，故对其做一定的简化。对阴、阳转子进行自动划分，之后对阴、阳转子网格数量进行加密，控制其全局网格尺寸为3 mm，保证网格尺寸对结果影响的无关性。其网格划分结果如图5所示。

(a) 阴转子 (b) 阳转子 图5 阴、阳转子网格划分

3.2 约束条件设置

根据阴阳转子实际工作过程，设置阴、阳转子进气口端只能绕Z轴转动和沿Z轴方向移动，将其他4个自由度全部限制；出气口端只能绕Z轴转动，限制其余5个自由度。

3.3 阴转子模态分析

根据双螺杆真空泵实际工作状况并查询文献[6-10]，施加约束以保证仿真结果尽可能接近真实值。

因篇幅原因，阴、阳转子均只展现其前4阶固有频率总变形云图。由图6和表1分析可知(其中图6阴转子左侧轴段为出气轴段，右侧为进气轴段)，阴转子的第1阶和第2阶固有频率相同，第5阶和第6阶固有频率相同，这是由于转子线型为对称型线，只是振动产生的变形方位不同而已。第1阶和第2阶均出现上下弯曲，最大变形量均发生在螺杆排气处的轴段部分且大小相同，只是振动变形的方位不一样；第3阶最大变形量出现在阴转子齿形表面，此时转子齿面出现一定程度的扭曲；第4阶最大变形出现在阴转子齿形表面及进气轴端，变形量由出气轴端向进气轴端逐渐增大；第5阶和第6阶均出现严重的扭转变形，最大扭转变形均出现在排气轴端部，且此时的变形量相对其他阶变形量最大。

3.4 阳转子模态分析

由图7和表2可知(其中图7阳转子左侧轴段为出气轴段，右侧为进气轴段)，阳转子也为轴对称结构，故其第1阶和第2阶固有频率相同、第3阶和第4阶的固有频率相同，只是振动发生的相位不同。阳转子的第1阶固有频率和第2阶最大变形一致，且最大变形均发生在排气轴端；阳转子的第3阶和第4阶固有频率一致，最大变形都发生在排气的轴端部位，出现上下弯曲，且此时变形量相对其他阶数的变形量最大；在第5阶固有频率下，螺杆有效工作段发生扭曲，最大变形出现在齿面；第6阶固有频率下，阳转子发生严重扭曲并伴随一定量的膨胀，最大变形出现在进气端及其伸出轴端。

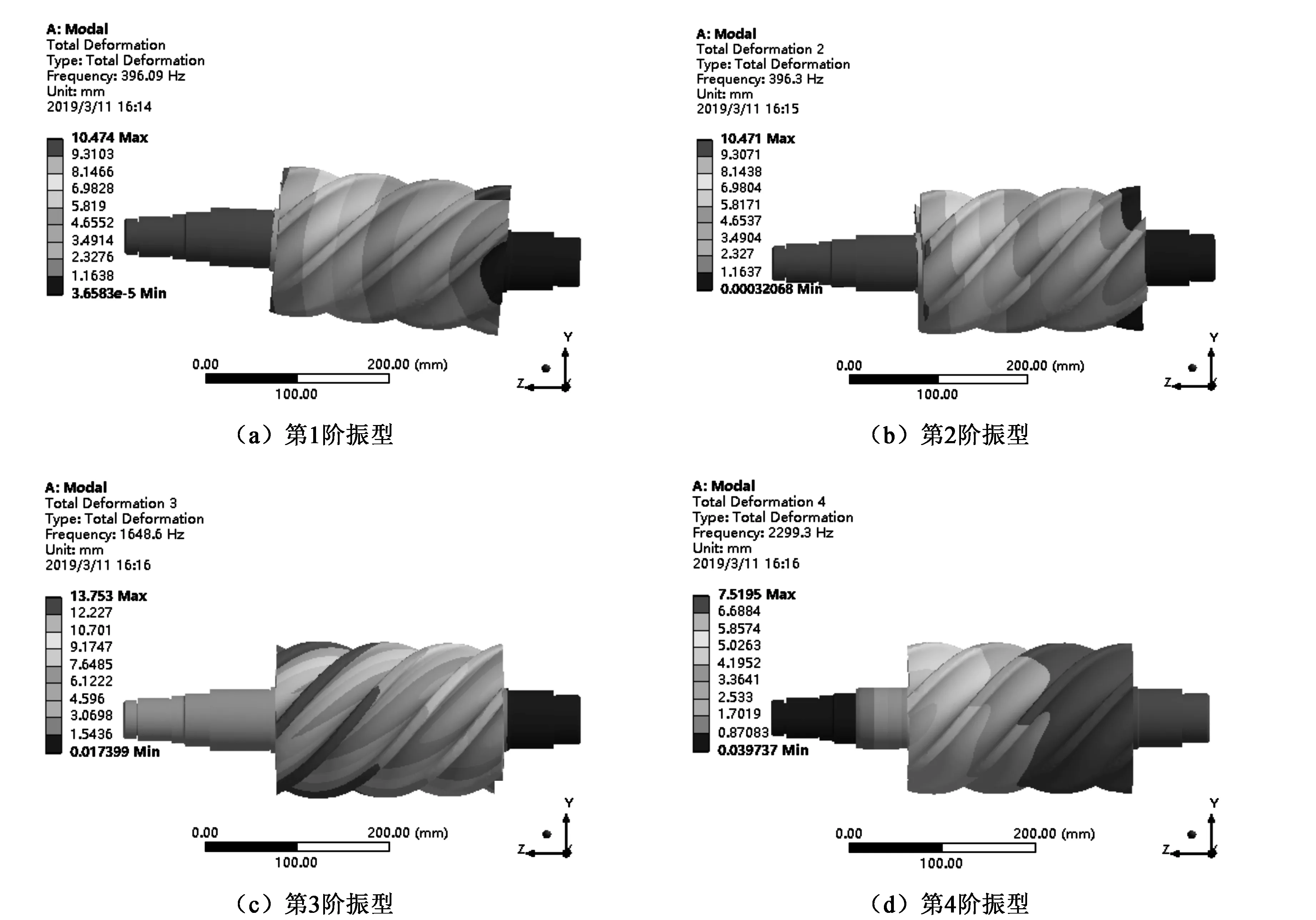
图6 阴转子前4阶固有频率总变形云图

图7 阳转子前4阶固有频率总变形云图

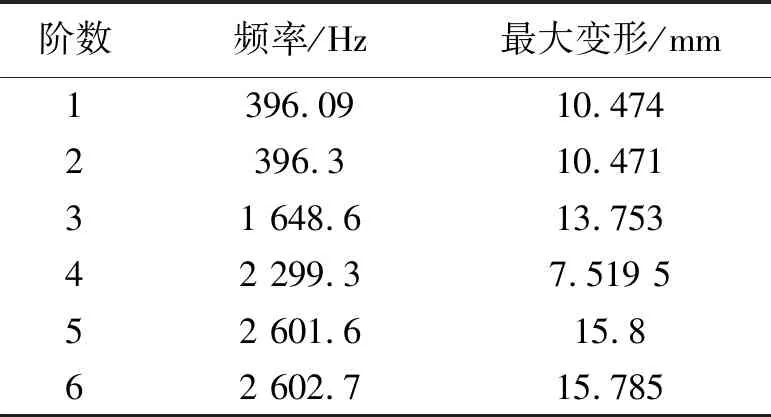
表1 阴转子前6阶固有频率及最大变形

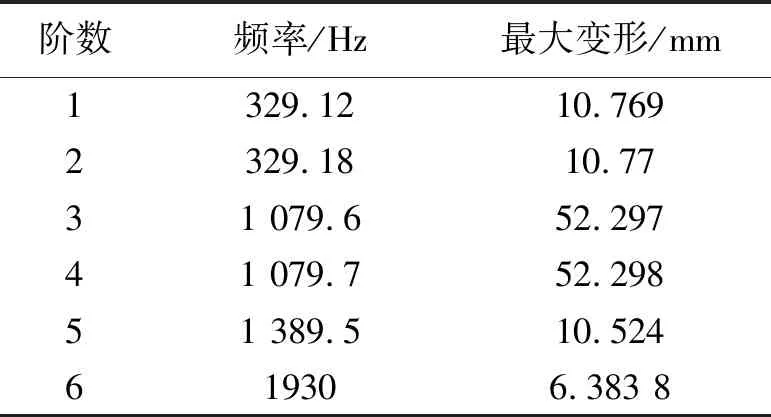
表2 阳转子前6阶固有频率及最大变形

3.5 共振检验

本文研究某厂的阴转子转速为2000 r/min，阳转子的转速为3000 r/min。阴、阳螺杆转子在对应转速下的激振频率fn(Hz)与转速n(r/min)之间的关系为[10]

(21)

求得阴、阳转子对应的激振频率分别为33.33 Hz和50 Hz，远远小于各自一阶固有频率，故在实际工作中不会产生共振。

4 结 论

本文对干式双螺杆泵的阴、阳转子进行建模和有限元模态分析，得出以下结论：

(1)根据齿轮啮合原理对阴、阳螺杆转子端面型线进行设计，保证了组成转子各段曲线依次连接的光顺性，为螺杆转子的生产制造提供了一定借鉴。

(2)阴转子第5阶和6阶固有频率时，相对其他阶数变形最大，且最大变形主要发生在排气口轴端；阳转子第3阶和4阶固有频率时，变形量远大于其他阶数时的变形量，其最大变形也主要集中在阳转子排气口轴端。

(3)对阴、阳转子工作时的激振频率进行计算，发现其远小于阴、阳转子各自一阶固有频率，故正常工作时不会发生共振。