成形磨齿机在线测量探头预行程误差研究及补偿

孙奇楠， 汪中厚， 马雅鹤， 刘欣荣， 廖志轩

(上海理工大学 机械工程学院， 上海 200093)

齿轮在线测量是指齿轮在磨齿机加工完成之后，无需将工件从机床加工位置拆卸便可以对其进行测量，避免二次夹装引起的误差，提高加工效率[1-3]。而在成形磨齿机上使用接触式探头进行在线测量时，当测球接触到工件上测点时会产生预行程误差[4-5]，Butler[6]认为，预行程误差约占测量总误差的60%，大大降低了齿轮测量精度。

因此，如何进行准确有效的标定，建立探头标定的数学模型，并且对误差进行补偿对整个测量系统的建立至关重要。吴彬彬等[7]对标定误差对齿廓误差测量的影响进行了理论分析，提出了标定误差的辨识及补偿方法；赵飞等[8]基于内置信号同步采集方法，利用齐次坐标变换原理对数控机床进给轴的内置信号进行变换分析，获得机床空间加工轨迹，从而实现机床加工误差的在线监测与评估；李光东等[9]运用多体系统理论分别建立了成形磨齿机几何误差模型，并进行了简化。

综上所述，国内外专家在测量方法和误差补偿上提出了很多可以参考借鉴的方法，但是并未涉及有关成形磨齿机测头预行程误差。因此，在此背景下展开研究，课题来源于上海理工大学与湖南某机电有限公司合作开发的L300G成形砂轮磨齿机。本文结合磨齿机的机构运动特点，采用BP神经网络方法对预行程误差进行部分实验数据训练，并建立预测模型，在对预行程误差进行补偿之后进行在线测量实验，以此证明预测模型的有效性。

1 预行程误差

1.1 预行程误差的计算

在用接触式探头进行在线测量时，因工件的表面具有不同形状，从不同法矢方向进行测量的探头预行程误差也不同，在做测量工具的精度校正时，通常都需要用精度更好的标准件去标定。本课题是采用标准量棒作为标定件，获得不同法矢方向的探头预行程误差。量棒是一个标准件，并且是一个圆柱形的机械结构，通过对标准量棒的测量可以得到不同法矢的预行程误差。如图1所示，通过测量P位置探头的预行程误差，即得到了此位置法矢方向(Y，Z)的预行程误差，从而当测量齿轮工件上相同法矢方向上的测点时，就可以根据测量量棒所得的预行程误差进行相应的补偿。

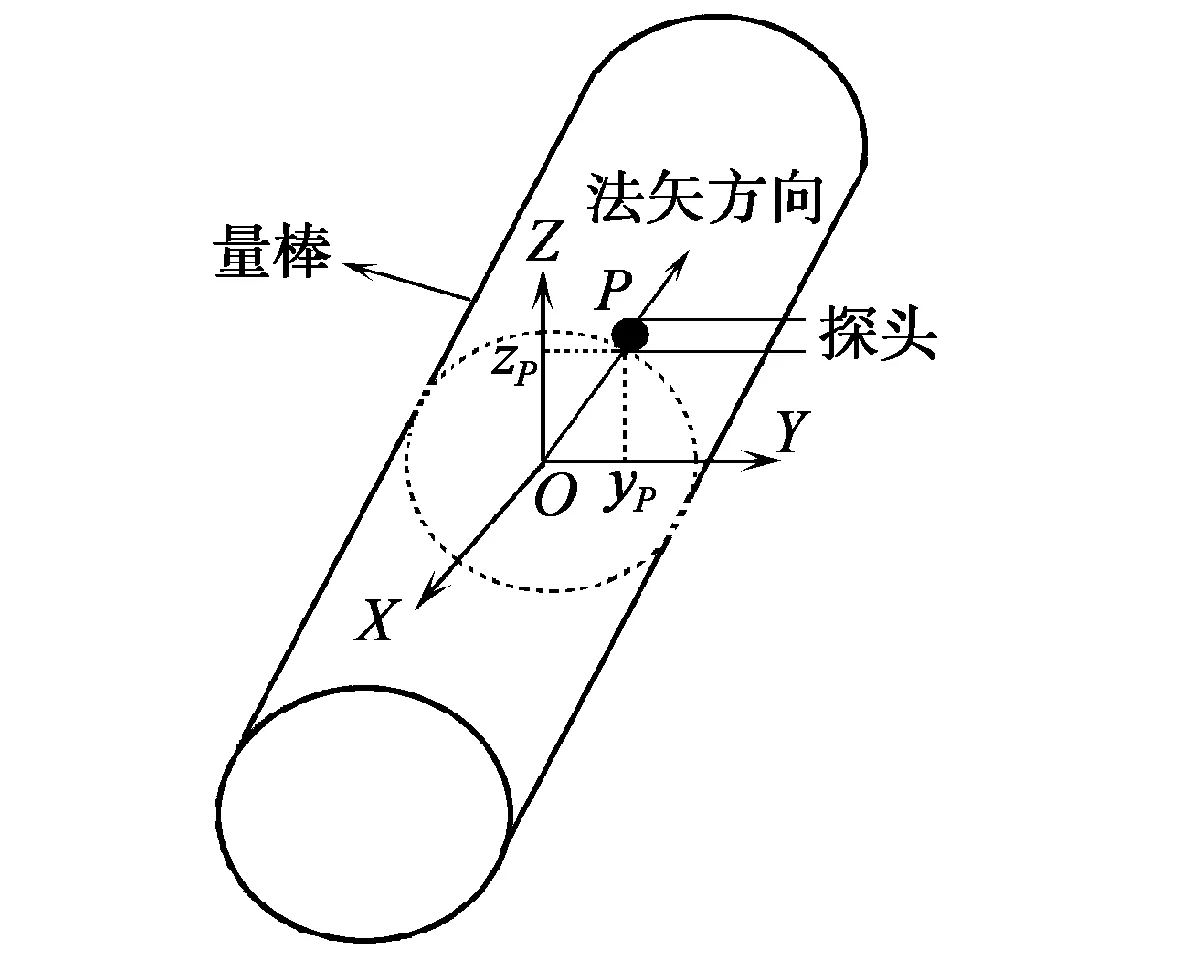
图1 测量量棒与输入向量

由分析可知，当接触测量量棒测量点时，机床主轴会继续沿着测量方向移动一小段距离。如图2所示，当探头的测球接触到测量点P时，由于产生预行程误差，探头会沿着测点P的法矢方向移动一小段距离，此时测球的中心已经从C移动到C′。根据几何关系图可以计算出预行程误差Δ的值：

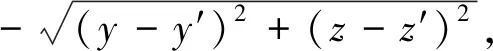
(1)

式中r探为探头的测球半径。

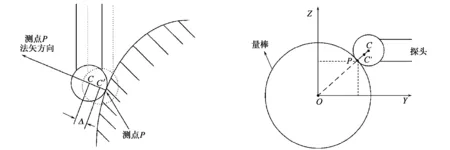
图2 预行程误差产生的示意图 图3 预行程误差计算示意图

求得预行程误差Δ的值，就可以得到预行程误差补偿的公式，并反求出测量点P(x，y，z)的机床坐标：

(x,y,z)=(x′,y′,z′)-(r探-Δ)·n，

(2)

式中n为测量点P的法矢方向。

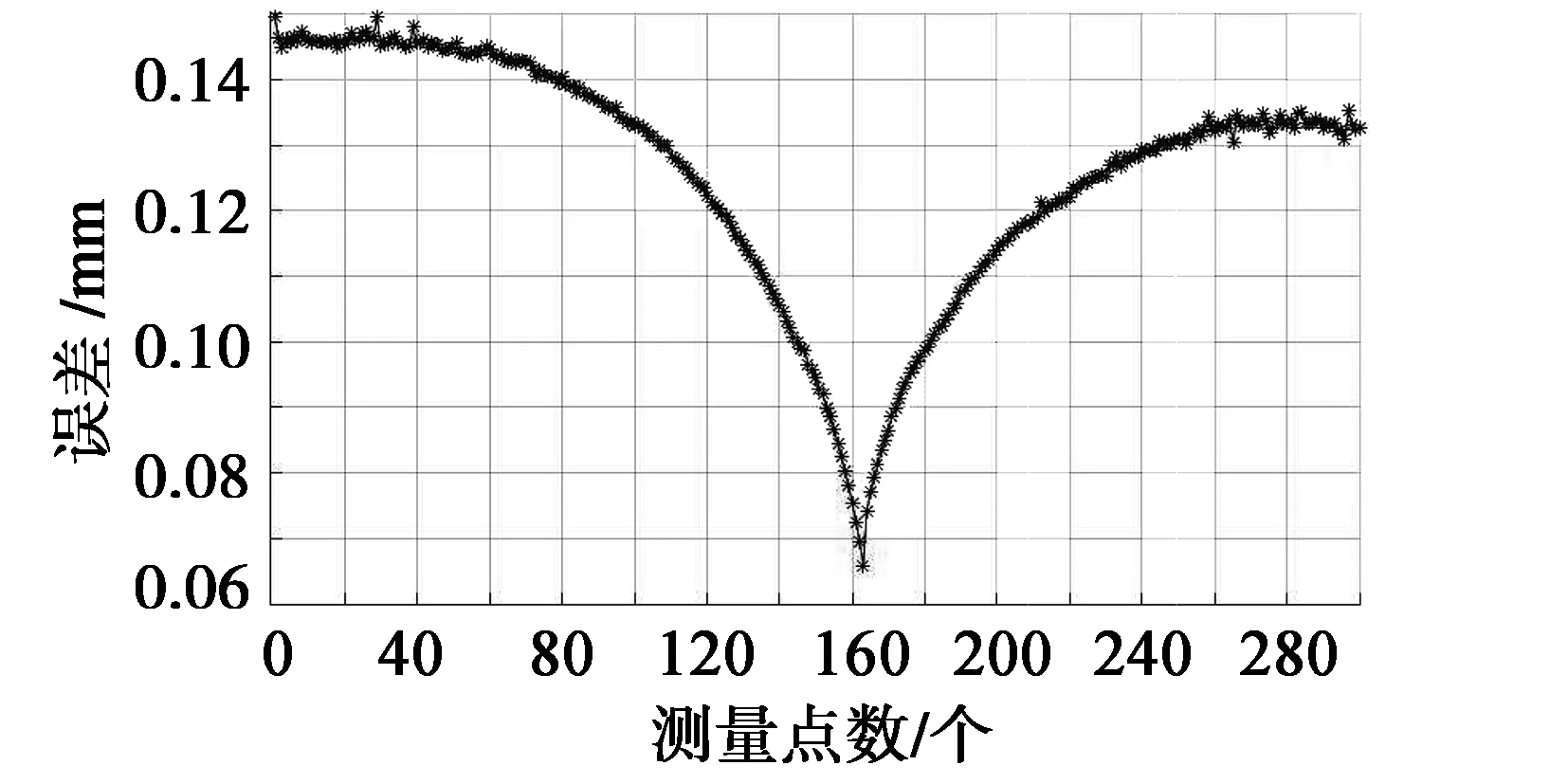
图4 不同方向的预行程误差

根据以上求解过程，通过对标准量棒的测量，可以获得不同法矢方向的预行程误差。本文采用的标准量棒直径为φ30 mm，接触式测量探头型号为Renishaw LP2H，探头直径为φ3 mm，为了尽可能取得多的测量数据，在量棒半圆圆周上，沿Y方向每隔0.1 mm测量一个点，总共获得300个测量点。如图4所示，得到了不同法矢方向的预行程误差图，并且经过多次实验，验证了实验数据的可靠性。

1.2预行程误差的补偿

本课题在线测量的对象是渐开线齿轮，渐开线齿轮传动结构简单、加工方便，应用也比较广泛，因此测量的齿面也是渐开线形状的，由渐开线的特性可以知道，当直线BK沿齿轮基圆做纯滚动，BK相切于基圆，AK是该圆的渐开线，即测点所在的线。如图5所示为齿面测量几何示意图，C点为探头中心位置，K点为测量点，B点是基圆上的切点，B点坐标为(xb，yb)，C点坐标为(0，yc)，基圆半径为rb，yc和rb是已知的参数，则由几何关系可求得B点坐标：

(3)

∠BOE=90°-∠BOC,

(4)

(5)

由以上公式，即可求得B点坐标，则测点K的法矢方向就是BC：

BC=(-xb,yc-yb)。

(6)

由测量量棒的过程可知，测量量棒时的测量方向已知，并且可以计算出测量时的测头预行程误差，由探头的工作原理可以推断，在测量齿轮的法矢方向和测量量棒时的法矢方向一致时，所产生的预行程误差是相近的，即可用量棒建立的预行程误差模型来获得测量齿轮时的测头预行程误差，用此误差值进行补偿计算，可以得到补偿后的齿面评价结果。

2 BP神经网络

2.1 BP神经网络方法

反向神经网络(back-propagation neural networks，BP神经网络)属于多层前馈逆误差传递的神经网络，该网络结构由输入层、隐含层和输出层组成。输入层接收输入信号，传导至隐含层模拟大脑神经进行处理，输出层显示结果。当输出结果偏离期望值时，网络运行反向传递，依据预测误差调节网络权值和阈值，缩小预测输出和期望输出之间的误差，直至满足精度要求。本文采用的是单隐层网络(三层前馈网)，如图6所示，包括输入层、隐含层和输出层。

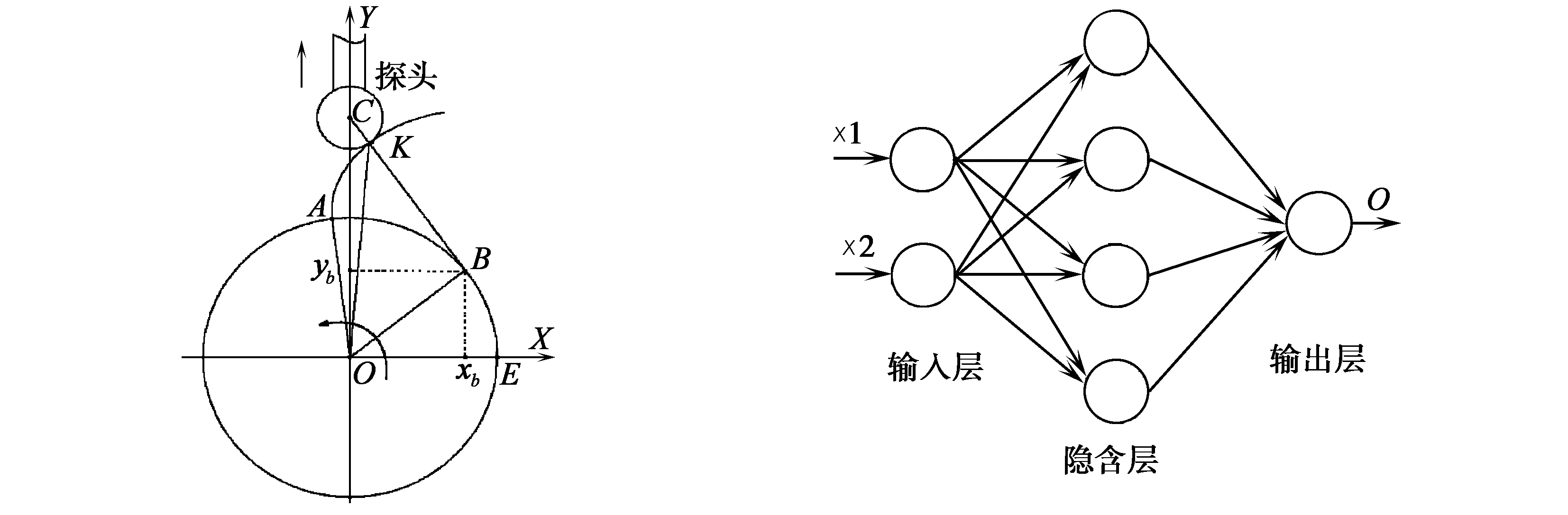
图5 齿轮测量几何示意图 图6 BP网络结构设计

(1)确定输入层：在本课题的三层前馈网中，输入向量X=(x1，x2)T，x1、x2分别为测量得到的接触式探头球心的坐标值(yp，zp)，见图1。

(2)设计隐含层：在建立BP神经网络模型时，隐含层神经单元的数目直接影响模型训练目标，一般来说，隐含层神经单元数目是综合经验公式采用试凑法确立而来，这样试出来的误差不一定最佳，所以找到合理的公式确定隐含节点数是问题的关键，本文根据高大启[10]提出来的公式计算隐含层神经单元数目：

(7)

式中m为隐含层节点数，n为输入层节点数，l为输出层节点数，将n=2、l=1代入求得m值为3.19，所以最终确定为m=4个隐含节点时，网络误差最小。

(3)确定输出节点：本课题设计输出层节点数为一个，即为在线测量系统的接触式探头测量的标准量棒上不同法矢的误差。

2.2 BP神经网络预行程误差预测模型的精度分析

由前面得到关于预行程误差值的300个实验数据，从中均匀选择150个测量值作为网络模型的训练数据，其余150个数据作为验证数据样本，训练数据经过遗传算法的BP神经网络模型训练后，可得到权值和预测模型，通过MATLAB编程实现建模，将预测的预行程误差结果值与实验数据中的验证数据样本进行对比，就得到预测模型的精度。预行程误差预测值如图7所示，带圈线条代表模型预测值，带星线条代表实际值。两条线的重合度反应了模型预测的精度，如图8所示，为预测结果和实际测量结果对比的差值，从图中可以很明显地看出，大部分的预测精度都在0.004 mm以下，具有较高的精度。

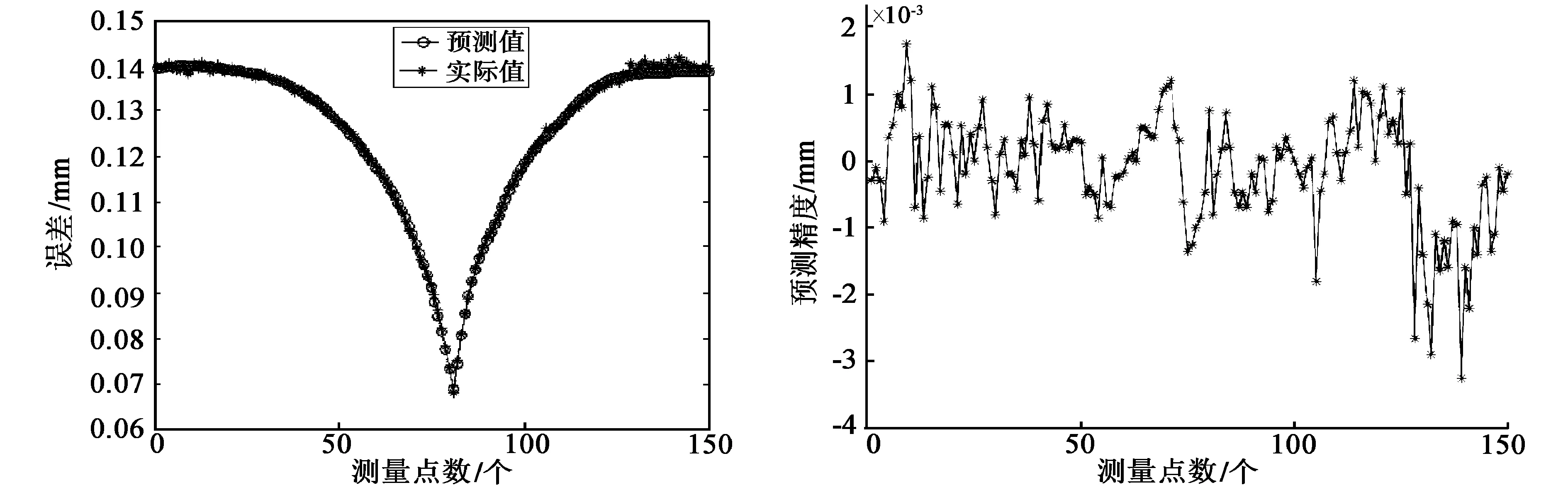
图7 预行程误差预测值 图8 预测模型精度

3 误差补偿

3.1 误差补偿分析

在成形磨齿机上对一个42齿的标准渐开线圆柱直齿轮进行齿形在线测量，先对标准量棒进行标定，获得测点数据作为BP神经网络的学习及测试样本，将测点数据导入设计好的网络中开始学习，学习结束后开始对齿轮进行测量。得到一系列测头中心的坐标值，即探头中心Z坐标值，以及探头在齿面切点上的具体坐标值，将这组数据导入到网络中完成对齿面测点数据的预行程误差预测，得到预行程误差值如表1所示。之后在软件中对预行程误差进行补偿。

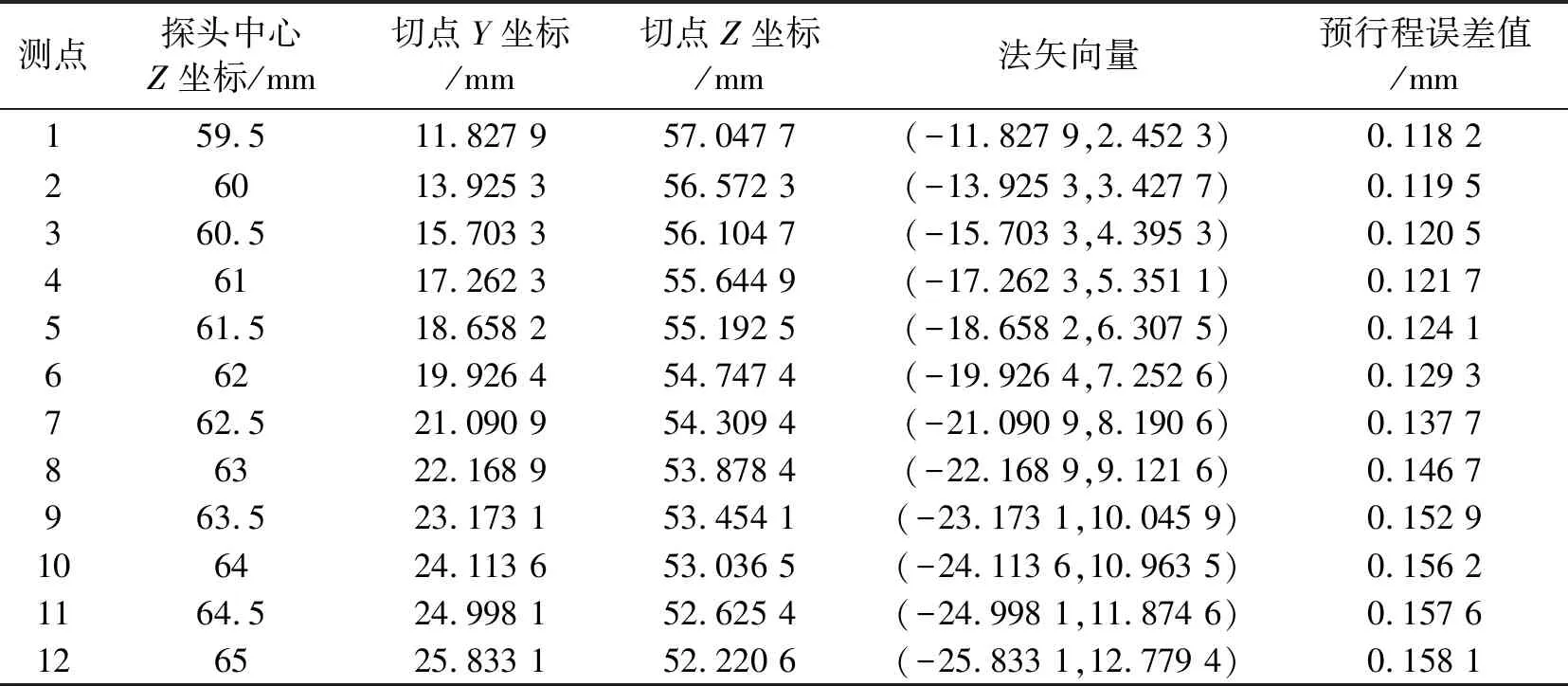
表1 预行程误差值

3.2 补偿结果对比分析

经过测头预行程误差补偿后，在同一齿面上得到的补偿结果与补偿前进行对比，如表2所示，补偿效果明显，精度改善很多，由此证明了补偿效果的有效性。补偿后齿形测量结果如图9所示。

表2 补偿后检测结果对比

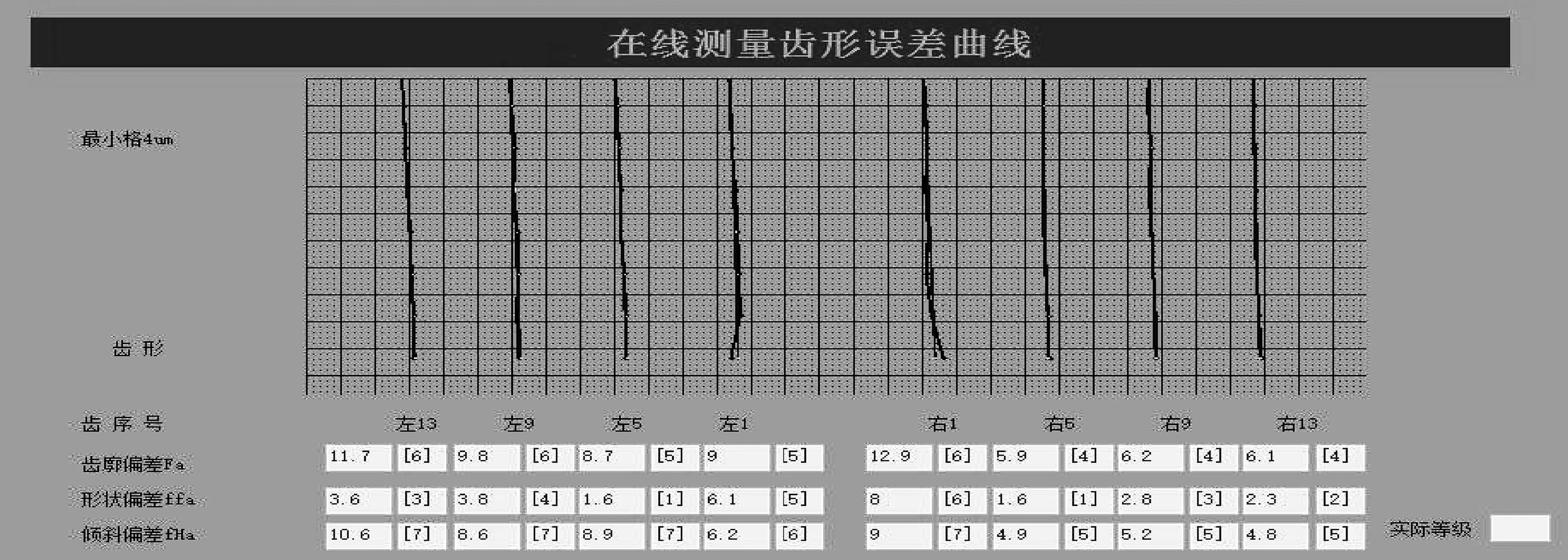
图9 齿形测量结果(补偿后)

4 结 论

本文先阐述了成形磨齿机在线测量探头预行程误差的计算过程，之后通过对量棒标准件的测量，通过MATLAB编程实现建模，基于BP神经网络对测量数据进行预行程误差的预测，将得到的预测值与验证样本的数据进行对比，误差精度满足要求，之后在测量软件中对预行程误差进行补偿并进行在线测量实验，通过实验结果表明补偿效果明显，精度改善很多，由此证明了预行程误差模型的有效性。

测头预行程误差占测头误差很大，但是国内研究者针对接触式测头误差的研究大多围绕测头标定及半径补偿，本次研究填补了成形磨齿机在线测量探头预行程误差的空白，具有一定的意义。