基于簧下设备弹性振动特性的轨道车辆动力学对比研究

戚 壮，刘鹏飞，王久健，陈恩利

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

轨道车辆簧下设备受到轮轨动态作用力的直接冲击，服役环境恶劣，工作载荷频率较高。当轮轨激振载荷频率与簧下设备自振频率发生重叠时，簧下设备的弹性模态可能被激发，进而导致更为剧烈的弹性振动。该共振现象不但影响簧下设备自身的结构强度，而且直接影响轮轨作用力，甚至对行车安全构成威胁。

在常规轨道车辆动力学计算中，各构件一般简化为刚体，即忽略构件自身的弹性振动，但对于激振频率与结构频率发生重叠或需要计算结构动应力时，则必须考虑构件自身的弹性特征[1]。文献[2—4]将车体作为弹性体进行动力学建模，不但提高了车体内部振动加速度的计算精度，而且能够得到车体的动应力分布，为车体结构设计提供借鉴。转向架构架作为关键承载构件，其刚柔耦合动力学模型在文献[5—7]中进行了讨论，为预测构架的疲劳寿命提供了有效方法。此外，弹性轮对的建模方法与其对整车动力学的影响也在文献[8—10]中进行了分析。文献[11]提出了研究路基柔性与车辆振动耦合的新方法，解决了刚柔耦合系统模态收敛判断的问题。

本文以某地铁探伤车搭载的探伤设备即簧下设备为研究对象，采用模态叠加法建立整车的刚柔耦合动力学模型，在考虑簧下设备的弹性特征基础上分析其在车轮不圆顺与轨道不平顺两种激振形式下的动力学响应及对整车动力学性能的影响，以期为车辆簧下设备的设计及悬挂方式的选择提供借鉴。

1 柔性簧下设备的建模及计算方法

1.1 柔性簧下设备物理坐标的表示方法

将某型地铁探伤车搭载探伤设备的搭载架视为柔性簧下设备时，其坐标表示如图1所示。图中：OXYZ为绝对坐标系；O′X′Y′Z′为固结在柔性体上的相对坐标系；R为相对坐标系的刚性位移；rP和uP分别为柔性簧下设备上任意一点P在OXYZ与O′X′Y′Z′中的位置向量。

rP与uP的关系可表示为

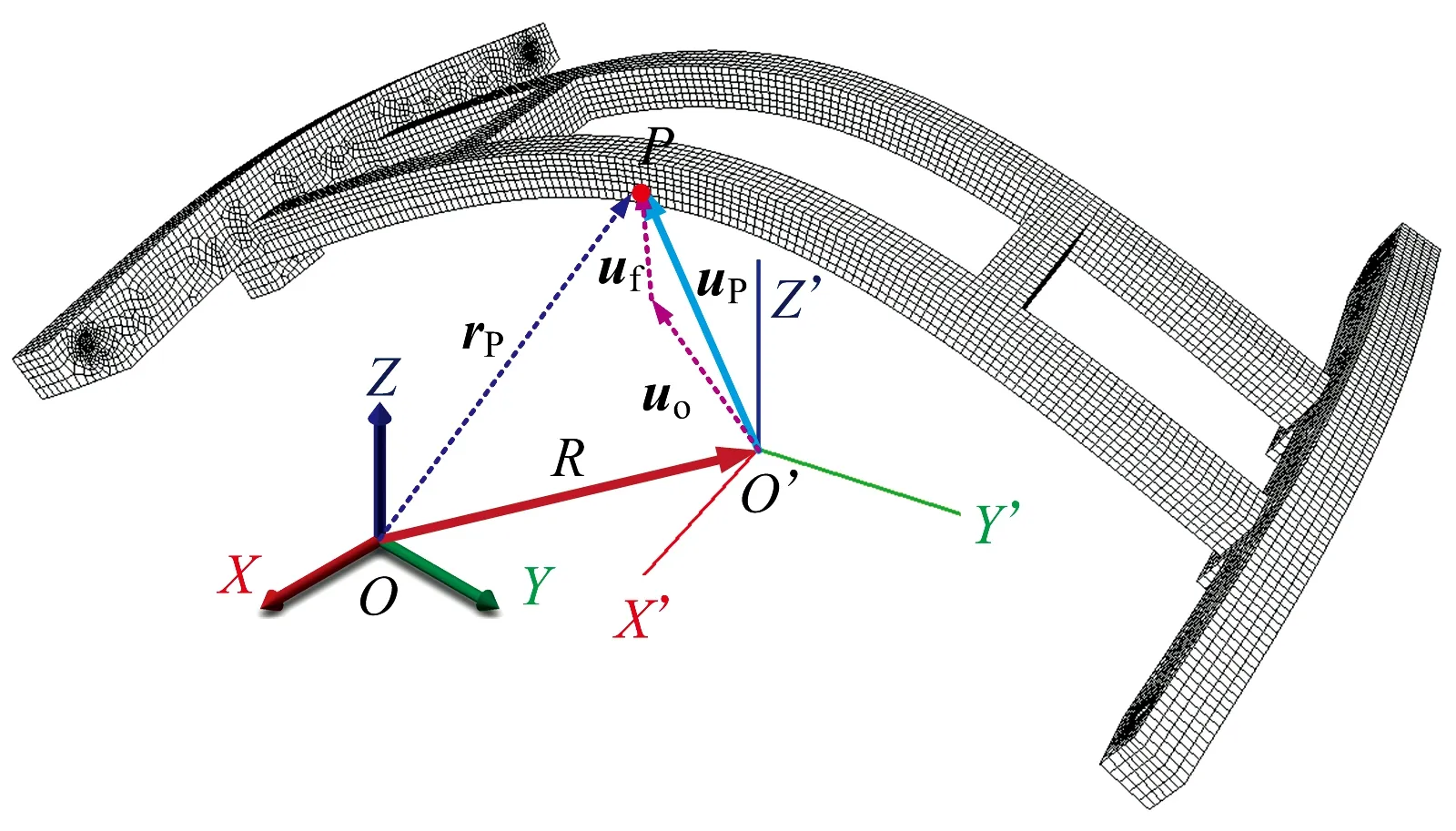
图1 柔性簧下设备的坐标表示

rP=R+AuP=R+A(uo+uf)

(1)

其中，

A=

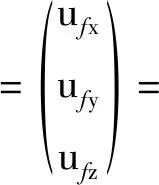
式中：uf为弹性形变向量；uo为柔性簧下设备未发生形变时点P的位置向量；A为相对坐标系发生转动而产生的坐标变换矩阵；θ0—θ3为欧拉四元数，由相对坐标系的旋转位姿确定。

当点P位置向量rP对时间求导时，考虑到uo在相对坐标系下为常向量，其对时间求导为0，可得到点P的速度向量为

(2)

式中：ω为相对坐标系的转动角速度向量。

继续对式(2)进行求导，可得到点P的加速度向量为

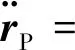
(3)

式中：α为相对参考坐标系的角加速度向量。

式(3)中等式右侧自左向右各项的物理意义分别为：相对坐标系的平动加速度项、法向加速度项、切向加速度项、科氏加速度项以及弹性变形加速度项。

由式(1)—式(3)可知，求解柔性簧下设备运动状态的关键在于求解弹性形变向量uf，该向量是与空间和时间耦合相关的物理坐标弹性形变向量uf(x,y,z,t)。由于1个连续柔性簧下设备上的点实际有无穷多个，即使将柔性体通过有限元离散也会得到数量巨大的节点坐标，加之uf的时空耦合性，为求解柔性体的动力学响应造成了困难，需要通过模态叠加法予以解决。

1.2 模态叠加法

根据Rayleigh-Ritz近似方法，柔性簧下设备的形变量可由模态展开，对时空变量进行解耦，即弹性形变向量uf可表示为[12]

(4)

其中，

Φ=(φ1φ2…φn)

qf=(q1q2…qn)T

式中：n为选取的柔性簧下设备模态阶数；Φ为模态矩阵；qf为柔性簧下设备柔性自由度的广义坐标矩阵。

根据式(4)，可以将柔性簧下设备在物理坐标下的自由度转化为模态坐标下的自由度。若不考虑柔性簧下设备的内部阻尼效应，此时其自由振动微分方程为

(5)

式中：Mf和Kf分别为柔性簧下设备的质量矩阵和刚度矩阵。

为了将该微分方程解耦求解，可将Mf和Kf转化为对角矩阵Mff和Kff，即要求Φ同时满足以下2式。

ΦTMfΦ=Mff

(6)

ΦTKfΦ=Kff

(7)

联立式(6)和式(7)求得

KfΦ=MfΦΛ

(8)

其中，

式中：k和m分别为对角矩阵Mff和Kff对角线上的元素。

将式(8)展开，得到

(9)

即

(10)

若φi有非零解，则其系数行列式为零，即

(11)

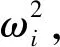
将Φ代入(5)式可化简为解耦的n个独立微分方程为

(12)

1.3 刚柔耦合振动微分方程

若将柔性簧下设备参考系的刚性位移R与位姿坐标θ考虑到转向架刚柔耦合模型中，则柔性簧下设备的广义自由度q可表示为

(13)

式中：qr为柔性簧下设备刚性自由度的广义坐标矩阵。

由式(15)可见，qr与qf的维数之和即为q的维数。

若对柔性簧下设备施加nc个约束，则其约束方程为代数方程，可表示为

C(q,t)=(C1(q,t)C1(q,t) …Cnc(q,t))T

=0

(14)

式中：C为1组独立的约束代数方程。

综上所述，柔性簧下设备在刚柔耦合系统中的运动方程可表示为

(15)

其中，

Cq=(Cij)

式中：Cq为雅可比矩阵；λ为nc维拉格朗日乘子向量，在某些情况下，λ中的元素为约束的反作用力；Qe为广义外部作用力向量；Qv为动能对时间和广义坐标求导产生的2次速度向量；下角标r代表刚性，下角标f代表柔性。

2 刚柔耦合模型

2.1 界面节点设置

首先对地铁探伤车簧下设备的几何模型进行有限元划分，再通过Craig-Bompton模态综合法得到簧下设备的模态矩阵，该模态矩阵由柔性体的静模态和特征模态2个部分综合而成。

计算簧下设备静模态时，需要选取若干个点为界面节点。界面节点一般设置在柔性体受铰接约束的位置或者外部力的作用位置；界面节点设置的最小数量应保证当释放某界面节点的单个自由度时，柔性体不能产生刚性运动。将地铁探伤车簧下设备的界面节点设置在转臂与搭载架的4个铰接点上，如图2所示。

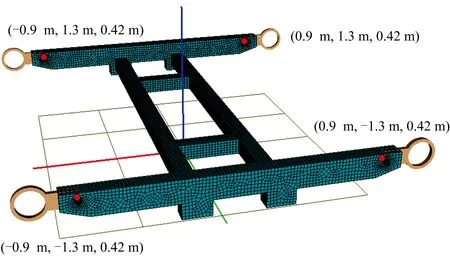
图2 界面节点位置

在界面节点设置约束为转臂对柔性体的3个方向的平动约束。由此计算出静模态的数量为3×4=12(个)；柔性簧下设备的刚性模态为6个方向的刚性运动自由度；此外再选取该柔性簧下设备的前50阶特征模态进行模态综合，则柔性簧下设备自由振动模态总数N自由振动模态=N静模态+N特征模态-N刚体模态=12+50-6=56(个)。

2.2 模态计算

通过对上述结构进行模态综合，得到其前56阶自由振动模态，即得到式(4)中的模态矩阵Φ，列数为N自由振动模态，行数为3N节点。其前5阶模态的自振频率与对应的振型如图3所示。由1.2节的分析可知，求模态坐标的振动响应，其物理本质在于求解各阶模态的振型在振动中的占比。

图3 前5阶模态的自振频率与对应的振型

2.3 动力学建模

常规车辆转向架动力学模型主要包括轮对、轴箱、构架3类刚体，以及由钢弹簧和减振器构成的一系悬挂装置。因以下研究中需要考虑簧下设备的柔性变形，则需要将探伤设备搭载架作为柔性体子结构导入到转向架多刚体动力学模型中。柔性体与多刚体模型的耦合建模方法如图4所示，其中多刚体模型在UM多体动力学平台上搭建；柔性体需要的模态矩阵、质量矩阵、刚度矩阵等在ABAQUS软件中通过有限元模型计算得到。

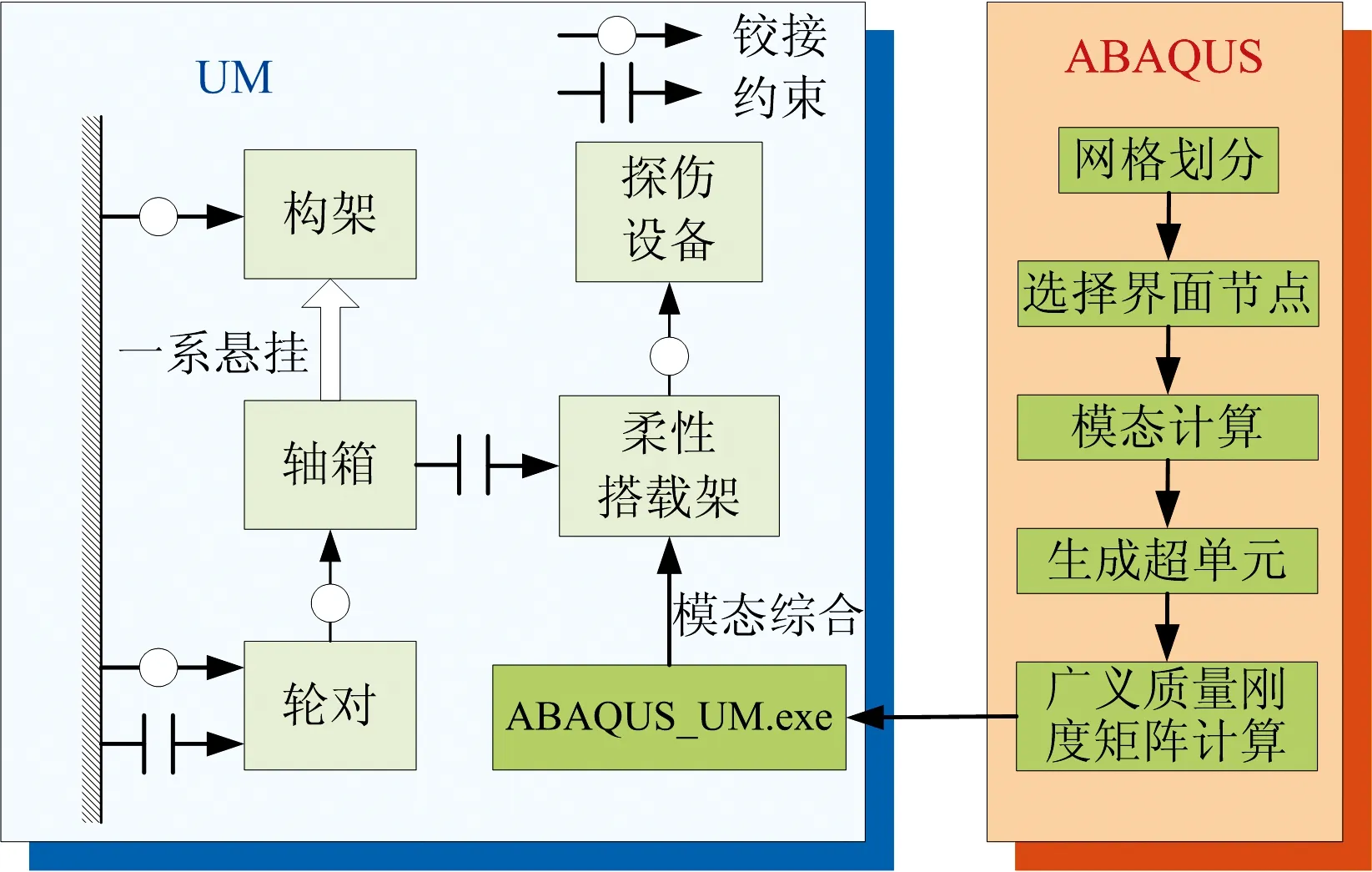
图4 多刚体模型与柔性体模型的耦合方法

在转向架刚柔耦合模型中，轮对相对于轨道具有6个自由度，在两侧轨道约束下，沉浮与侧滚是非独立自由度；轴箱相对于轮对具有点头自由度；构架通过一系悬挂坐落在4个轴箱上；柔性搭载架导入后，其4个界面节点分别被4个轴箱通过铰链约束，探伤设备直接铰接在搭载架上，故搭载架与探伤设备均属于簧下质量。由于另一转向架为动力转向架，无探伤设备，故将其作为多刚体系统进行建模。将2个转向架作为子系统，并通过二系悬挂与车体进行连接，得到的整车车辆刚柔耦合动力学模型如图5所示。

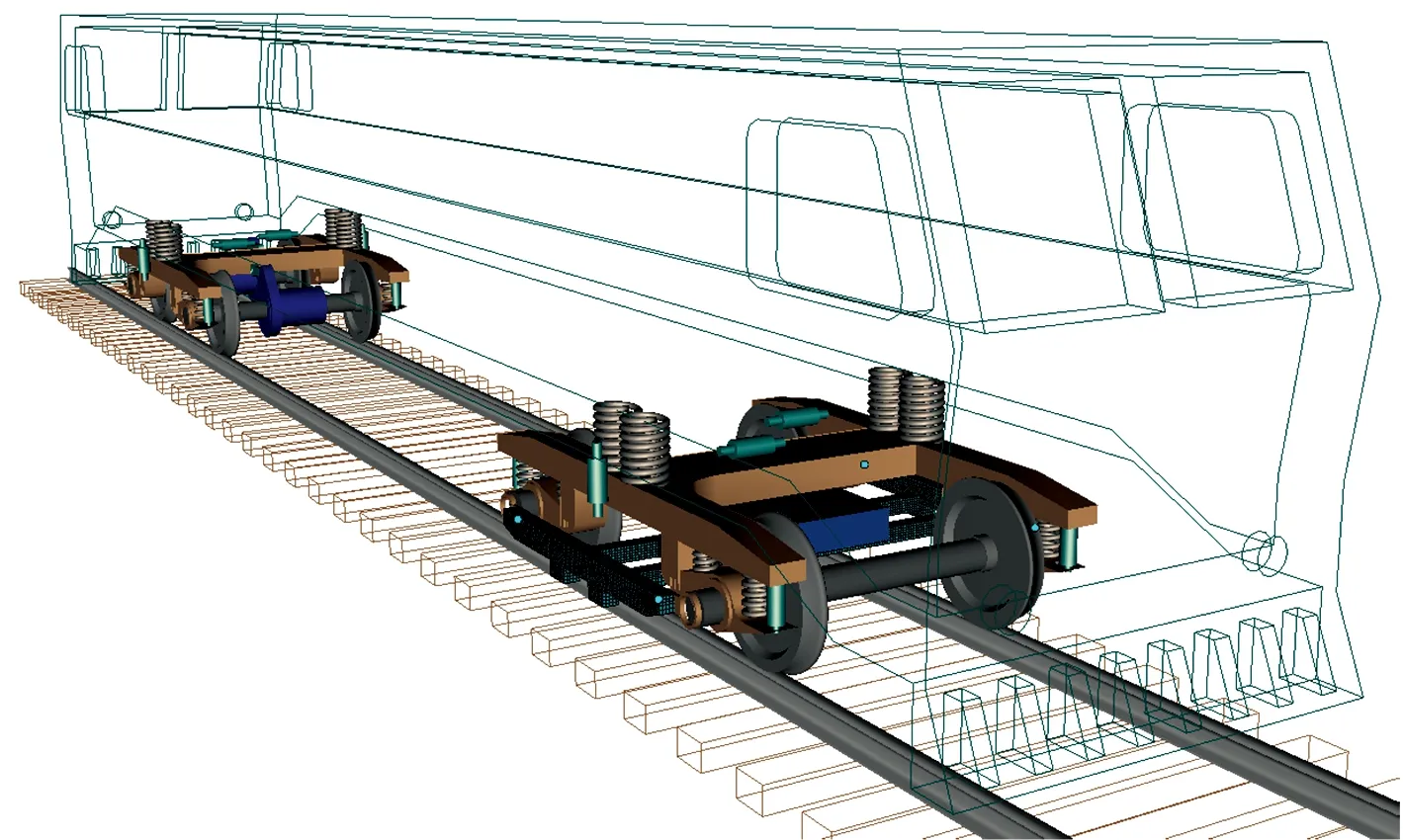
图5 车辆刚柔耦合动力学模型

3 振动响应分析

3.1 簧下质量线性振动响应

为了研究簧下结构振动响应与轮轨激振频率的关系，首先对簧下质量的线性振动响应进行分析。在搭载架4个界面节点均被约束的状态下，考虑搭载架的柔性特征，计算簧下探伤系统(搭载架+探伤仪器)的线性振动模态与固有频率。由于车辆运行时振动的主要能量集中在40 Hz以内[13]，故研究其前4阶模态(第5阶模态固有频率为57.7 Hz，>40 Hz，不研究)的自振频率与对应的振型如图6所示。

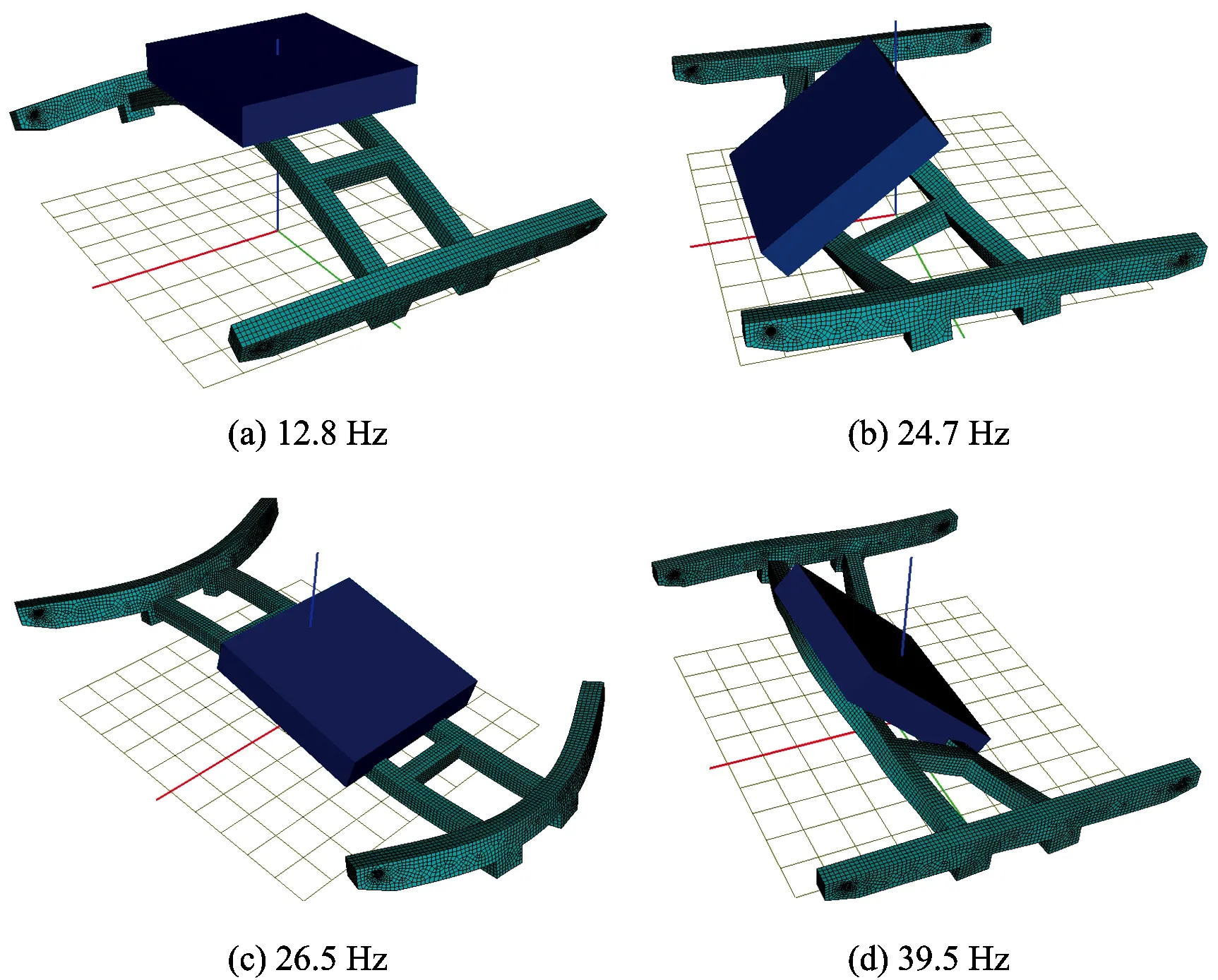
图6 簧下质量前4阶模态的自振频率与对应的振型

由计算结果可知：第1阶模态和第3阶模态分别为簧下质量的垂向振动和横向振动，对应的自振频率分别为12.8和26.5 Hz；当探伤车在轨道上运行时，轮轨动作用力易激起簧下质量的以上2种模态，直接影响探伤设备的振动响应与车辆动力学指标。

3.2 车轮不圆顺下的弹性振动响应

车轮不圆顺为轨道车辆运行中常见的周期激扰源，其激扰频率与车辆运行速度直接相关。根据现场实际运用经验[14]，研究中设置的车轮不圆顺如图7所示。图中：L为扁疤长度，取50 mm；L1为车轮材料塑性变形产生的过渡圆弧，取10 mm。

图7 车轮不圆顺示意图

设置轨道为理想平滑轨道，搭载架视为柔性体，计算车轮不圆顺激扰下簧下设备垂向振动的位移和振动加速度与车速的关系，结果如图8所示。由图8可知，簧下设备在车速为120 km·h-1左右振动最剧烈，其垂向振动位移达到1.2 mm，振动加速度达到6.6 m·s-2。

对上述结果进行分析，车轮半径为420 mm，则车速为120 km·h-1时，车轮不圆顺产生激扰频率为12.6 Hz。对比3.1节簧下质量线性响应的计算结果，120 km·h-1车速下车轮不圆顺的激扰频率刚好与簧下质量的1阶振动频率12.8 Hz基本吻合，即探伤设备的1阶固有模态被车轮不圆顺激发。

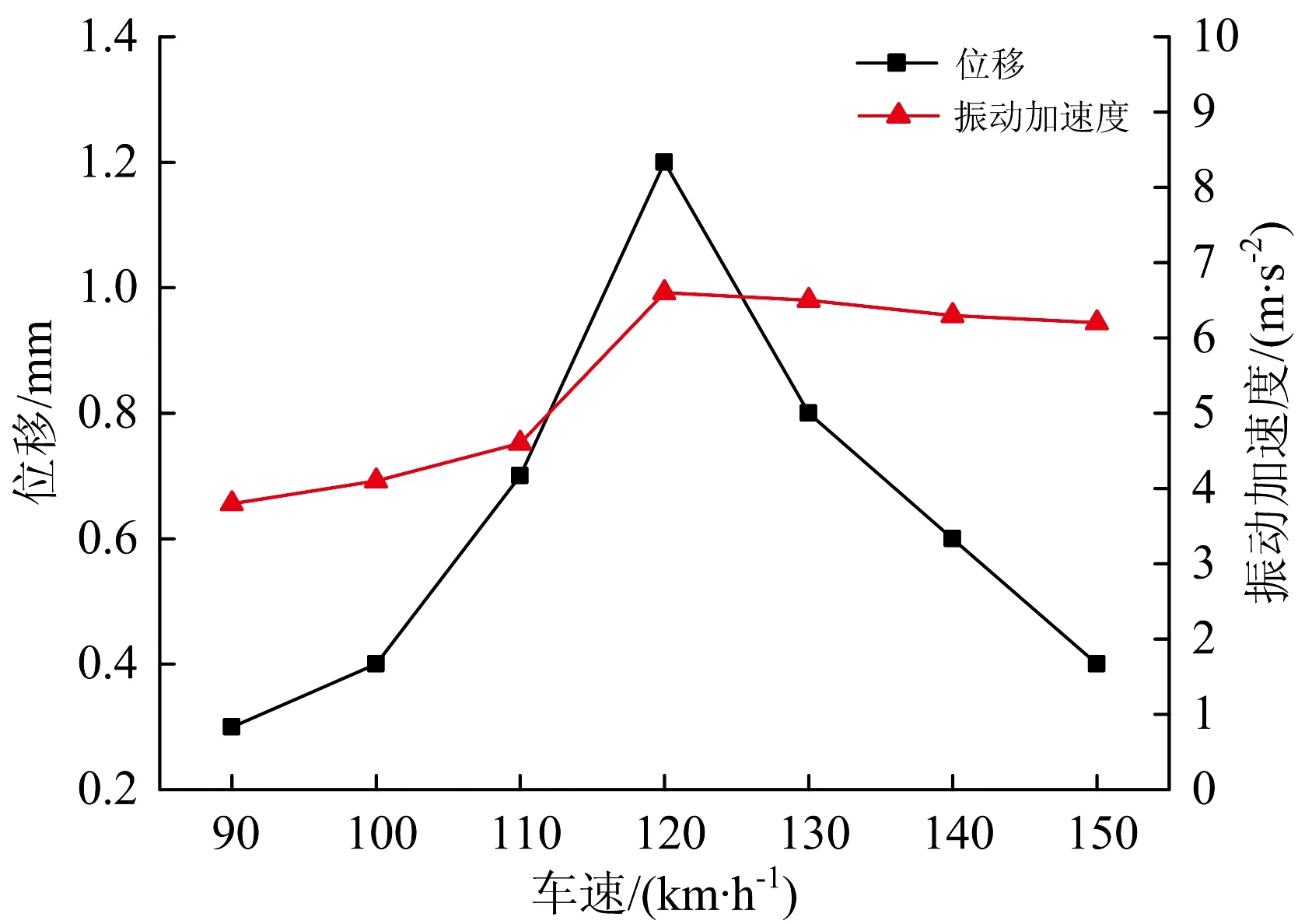
图8 车轮不圆顺激扰下簧下设备振动的位移和加速度与车速的关系

将搭载架由柔性体替换为刚性体重新进行上述计算，发现振动位移为0.4 mm左右，且不随车速的改变发生变化；簧下质量的振动加速度急剧升高至180 m·s-2左右，说明搭载架的柔性特征对探伤设备起到了较好的缓冲作用。计算簧下设备振动响应时，应该考虑搭载架的柔性特性，使分析结果更接近真实情况。

3.3 轨道随机不平顺下的弹性振动响应

轨道不平顺通过轮轨相互作用直接传递至转向架，激发车辆系统的随机振动。设置轨道不平顺为美国V级谱，车辆以120 km·h-1的速度在轨道上运行，搭载架分别视为柔性体和刚性体进行建模，计算簧下质量垂向和横向的振动加速度时域响应如图9所示。由图9可知，除刚性搭载架的垂向振动加速度在个别点发生刚性冲击外，柔性搭载架的振动加速度响应整体高于刚性搭载架。

将该时域响应进行傅里叶(FFT)变换为簧下质量垂向和横向的振动加速度频域响应，得到柔性与刚性搭载架的频域对比结果如图10所示。由图10可知，柔性搭载架的垂向和横向振动加速度的振动能量分别集中在12和28 Hz左右；而刚性搭载架的则分别集中在10～100和1～50 Hz这2个区域内均有分布，未发现能量集中峰值。联系3.1节簧下质量线性振动响应的计算结果，柔性搭载架的振动能量峰值分别对应其1阶垂向振动与3阶横向振动的固有频率，体现了簧下设备在车辆运行中的结构弹性振动特征。

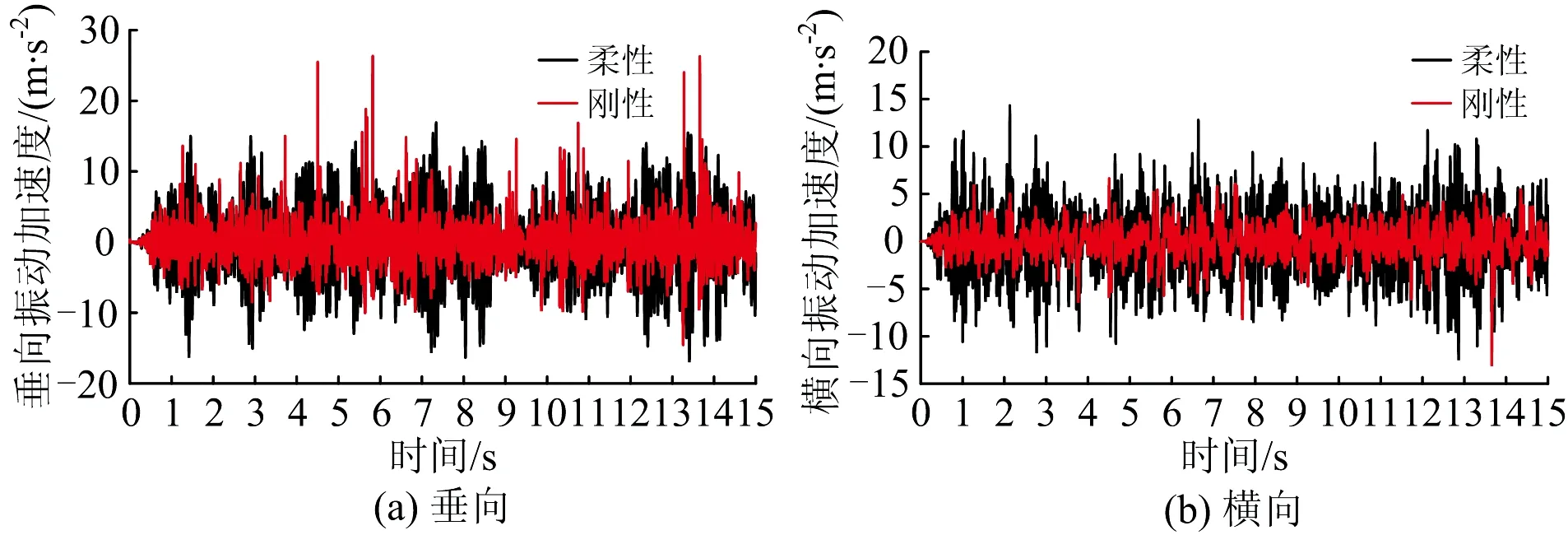
图9 轨道不平顺下簧下设备的振动加速度时域响应

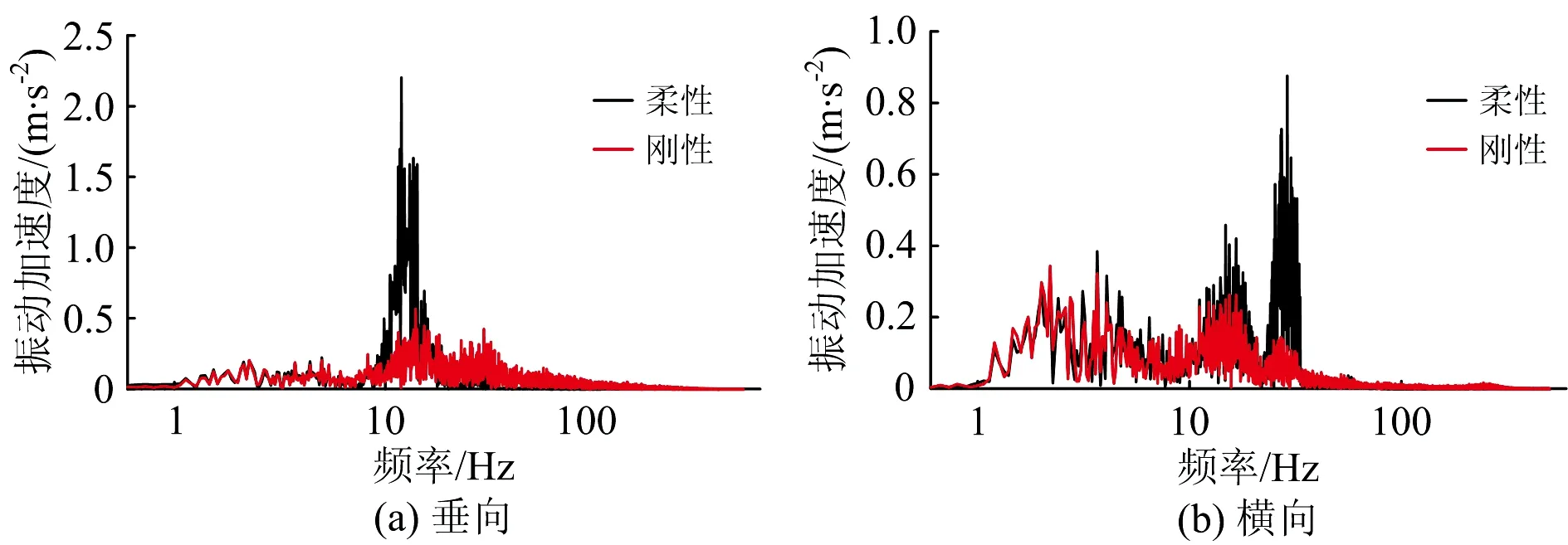
图10 振动加速度的频域响应

为了研究车速与簧下设备弹性振动的关系，分别以40～100 km·h-1车速进行计算，以相同的方法对簧下设备的横向、垂向振动加速度进行频域分析，结果如图11所示。

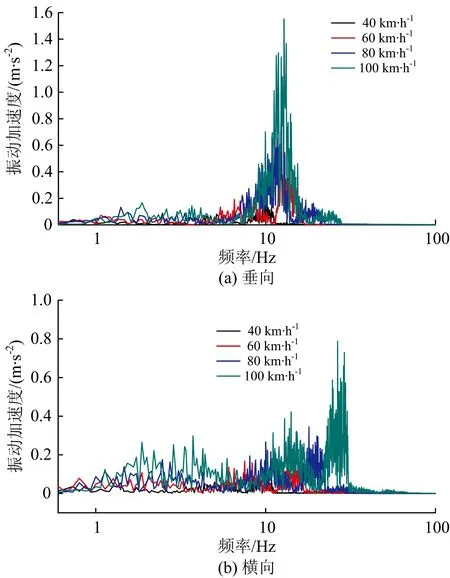
图11 不同车速下振动加速度的频域响应

由图11可知，当车速为40 km·h-1时，垂向振动加速度未发现能量集中，故簧下设备垂向弹性振动未被激发；同理，横向振动加速度在车速为100 km·h-1时才出现能量集中，说明簧下设备横向弹性振动在车辆高速运行时才被激发。上述计算结果还表明，只要簧下设备的弹性振动被激发，其不同车速下的垂向和横向振动加速度的能量均集中在12和28 Hz左右，说明簧下设备的弹性振动频率只与自身结构模态频率相关，与车速无关。

对于该型地铁探伤车，在正常80 km·h-1车速运行状态下，簧下设备的横向弹性振动不会被激发，但其垂向弹性振动会较为剧烈。为了降低该车簧下设备的垂向弹性振动，可适当增加搭载架横梁的结构刚度，使结构模态频率高于轮轨激扰频率，进而降低弹性振动对探伤设备的影响。

4 簧下设备对车辆动力学性能的影响

为了研究簧下设备对整车动力学性能的影响，在簧下设备原始模型1的基础上，建立其对比模型：其中对比模型2去除柔性搭载架等簧下设备；对比模型3在转臂支撑点处加装弹性橡胶关节，其径向和轴向刚度分别为14和5 MN·m-1，安装方式如图12所示。

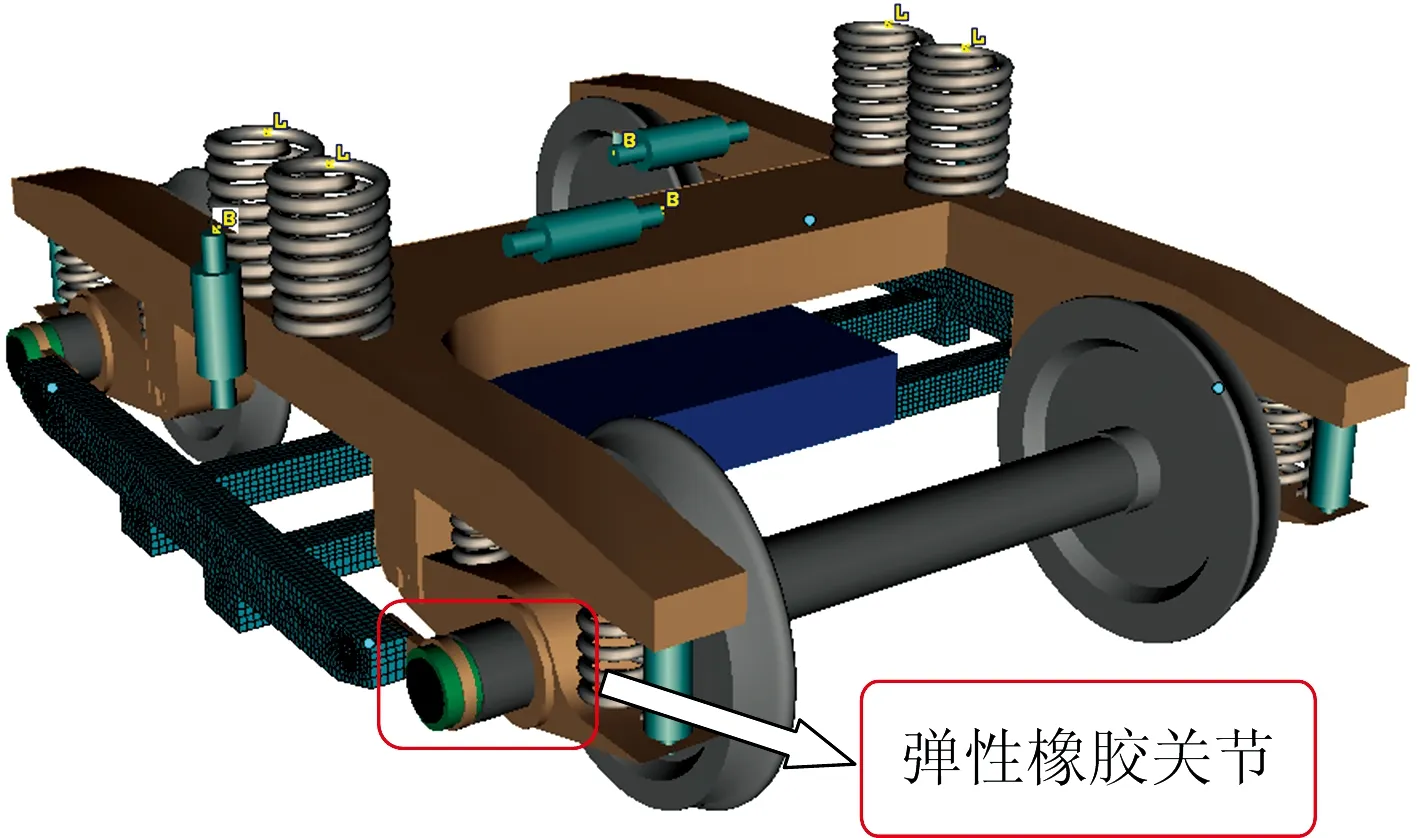
图12 转向架模型中增加弹性橡胶关节的安装方式

相应的，针对原参数车辆、无簧下设备车辆和增加弹性橡胶关节车辆3种车辆动力学模型，分别从稳定性、平稳性、曲线通过性3个方面进行对比研究。

4.1 稳定性

在理想平滑轨道上设置一段不平顺，车辆以不同车速通过，观察轮对横移量是否收敛，以计算车辆的临界速度。3种车辆动力学模型的轮对横移量时域历程分别如图13所示，它们的临界速度分别为180，211和192 km·h-1。由图13可知，簧下设备带来的轮对运动约束会导致车辆稳定性较无簧设备时下降14.7%左右；对簧下设备增加弹性橡胶关节有助于提高车辆稳定性，可使临界速度提高约7%。

4.2 平稳性

将3种车辆动力学模型分别以50～110 km·h-1的车速运行在美国V级谱线路上，对车体的振动加速度进行数据处理得到Sperling平稳性指标如图14所示。由图14可知，簧下设备对车辆平稳性指标的影响不大，说明簧下设备的振动对车体振动平稳性的影响较小。

图13 稳定性计算结果

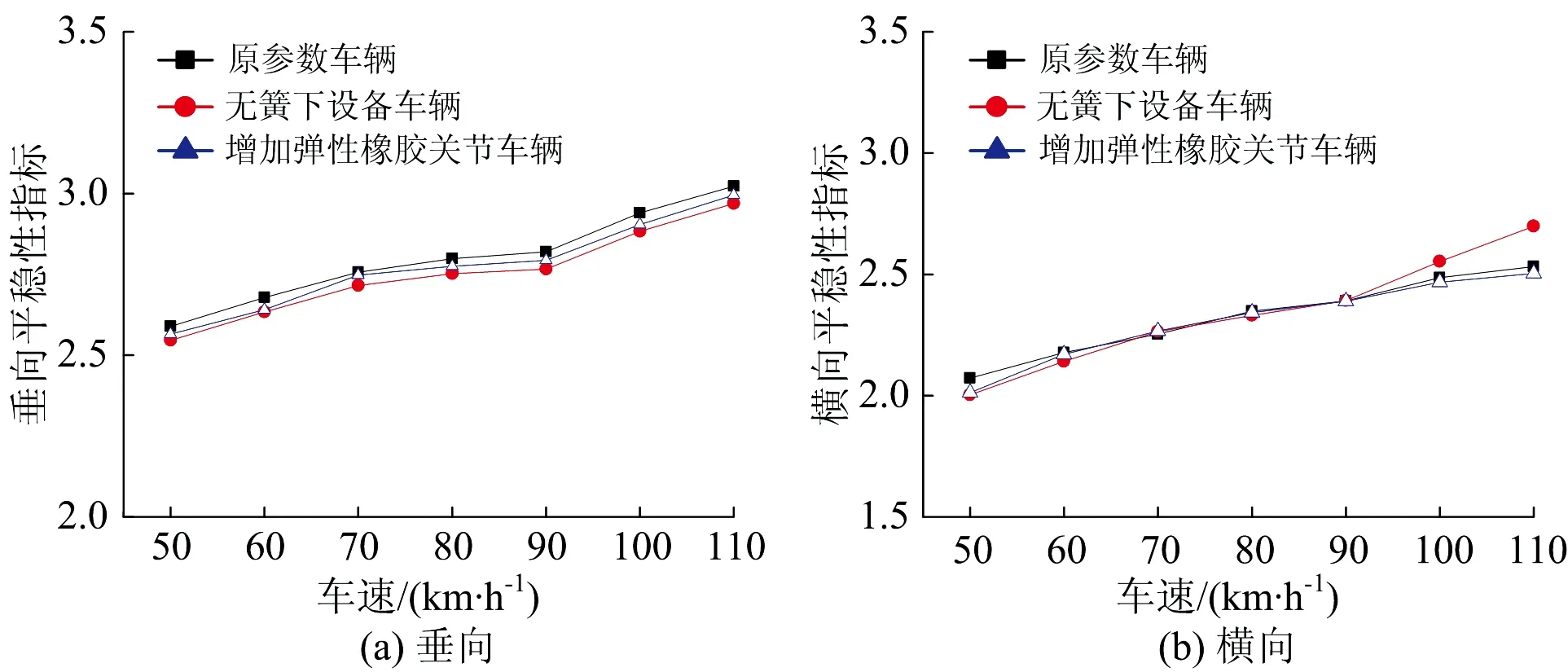
图14 平稳性计算结果

4.3 曲线通过性

设置车辆通过R300 m半径曲线，曲线超高设置为120 mm，缓和曲线长度120 m，分别以轮轨横向力、脱轨系数、轮重减载率、磨耗指数4类指标评判车辆的曲线通过性，仿真得到3种车辆动力学模型这4项指标随车速的变化关系如图15所示。

由图15可知，原参数车辆模型中，刚性连接的簧下设备导致车辆曲线通过性能的各类指标提高了约20%；增加弹性橡胶关节后，各类曲线通过性指标能够降低约10%。该动力学特性产生的原因主要在于，簧下质量的增加使轮轨之间的动态作用更加剧烈，且搭载架对轮对的约束作用也影响了车辆通过曲线的能力，从而导致车辆的曲线通过性变差；对簧下设备增加弹性橡胶关节后，缓解了轮轨的刚性冲击，降低了轮对的摇头刚度，从而能够在一定程度上改善车辆的曲线通过性能。

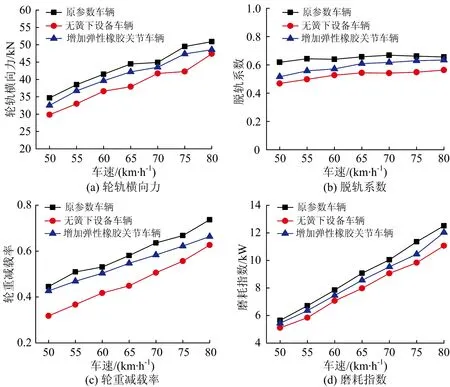
图15 曲线通过性计算结果

5 结 论

(1)模态叠加法使柔性体的物理坐标转换为模态坐标，进而实现柔性变形时间相关性与空间相关性的解耦，大大缩减刚柔耦合动力学模型的自由度。

(2)车辆簧下设备垂向和横向振动的线性振动响应频率分别为12.8和26.5 Hz；当车速为120 km·h-1时，车轮不圆顺产生的激扰频率刚好与簧下设备垂向自振频率吻合，导致簧下设备振动加剧。

(3)相比于刚性模型，柔性模型簧下设备的振动能量主要集中于柔性体的自振频率，说明轨道不平顺能够激发簧下设备的弹性振动。

(4)车速高于某特定值时才能激发簧下设备的弹性振动，且弹性振动能量集中频率不随车速的变化而变化。

(5)簧下设备虽对车辆运行平稳性影响不大，但会降低车辆的稳定性与曲线通过性，通过对簧下设备增加弹性橡胶关节悬挂，能够使车辆的各类曲线通过性指标降低约10%。