正断层错动下乌鲁木齐地铁1号线隧道结构受迫影响研究
孙 飞,张志强,秦 昌
(1.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031; 2.西南交通大学 土木工程学院,四川 成都 610031)
因我国西部地区断裂构造密集的地理特征,随着西部城市地铁的修建,地铁隧道将不可避免地要穿越活动断层破碎带。断层错动对隧道工程的影响主要表现为错动破坏和地震破坏[1]。断层错动会在短时间内使隧道结构出现很大的受迫变形及应力,对隧道工程的安全与稳定造成巨大隐患。因此,研究断层错动作用对地铁隧道结构的影响,成为保障隧道工程安全的关键性课题。
近几年国内外已出现一些断层错动影响隧道结构受力的研究成果。刘学增等[2-3]通过几何相似比1∶50的正断层错动模型试验及数值模拟,研究了在不同错动位移条件下分段式隧道结构受力、围岩压力分布以及塑性应变;雷军等[4]对乌鞘岭隧道F7断层区段各项应力和收敛变形进行了监测,分析了围岩、衬砌受力及变形变化趋势;黄强兵等[5-7]通过缩尺几何相似比为1∶5的地裂缝活动模型试验和数值模拟计算,研究了西安地铁2号线隧道正交穿越地裂缝带的设防参数、地裂缝对地铁隧道的影响机制及病害控制方法;熊炜等[8-9]通过有限元方法探讨了正断层环境下公路山岭隧道结构的受力及变形规律;邵润萌等[10]通过建立有限元模型对不同类型断层在错动作用下导致的隧道工程损伤及岩土失效扩展机理进行了研究;郑升宝等[11-12]分析了大量穿越断层隧道的破坏情况,对隧道因断层活动而受到破坏的特点做了总结。
这些既有研究成果中仍存在一些不足:数值分析中一般多采用连续模型,无法表征“断层面附近隧道与围岩的接触关系在错动发生时的变化”,导致数值模拟结果与实际不符;现有试验模型的比例尺都较小,特别是缺乏对隧道纵向尺度方向的考虑,导致试验所获得的隧道结构破坏范围存在显著误差;模型中对于断层的模拟,均未在装备上消除“机械摩擦”,无法保证断层错动的有效性。
本文以乌鲁木齐地铁隧道穿越九家湾活动断层工程为依托,考虑活动断层错动作用下地层—隧道结构的相互作用,建立惯性力—强制位移连成作用的地层荷载结构模型,采用“接触面”模拟“断层面”及“围岩与隧道相互作用面”的力学行为;在大比例尺跨活动正断层隧道剪切错动模型试验中,研制大比例、高精度、宽控速的断层错动室内同步加载试验装置,最大程度降低室内模型试验中边界效应的不利影响,使室内试验工况更贴近实际工况;通过数值模拟与模型试验相结合的方法,研究不同断层错动量下隧道结构应力应变的分布规律,探明隧道结构受迫行为及破坏范围。
1 工程概况
九家湾活动断层组分布在九家湾一带的中更新世洪积台地上,主要由4条走向NE(北偏东45°~60°)、呈大致等间距平行排列的1组正断层构成。每条正断层表现为由倾向相对的正断层构成地堑构造,主断层面倾向NW,倾角(60°~85°)较大。断层在地表形成北低南高的断层陡坎和宽数米至数十米、深1.0~2.5 m的断层沟槽地貌。断层地表破裂保留较完整清晰,经勘察认定为全新世活动断层,未来有百年内产生地震地表错动的可能。
2 模型建立及参数选取
取断层面前后各100 m范围建立计算模型,模型长×宽×高为200 m×40 m×40 m,隧道埋深取15 m,断层倾角取60°。断层破碎带位于隧道线路上方且宽度较窄,可将断层破碎带简化为断层面考虑,土体假设为理想弹塑性材料,采用Drucker-Prager屈服准则,变形缝假设为理想弹性材料。依据标准GB 50010—2002《混凝土结构设计规范》的规定,对衬砌混凝土自定义弹塑性应力—应变本构关系。初期支护混凝土等级为C25;对于二次衬砌混凝土,考虑钢拱架、钢筋网共同作用,其强度等级取C45,并采用整体式配筋方法研究裂缝分布特征。隧道二次衬砌每25 m设置1处变形缝,变形缝宽度0.1 m。模型前后、左右边界施加水平位移约束,上部边界为自由边界,底部边界施加竖向位移约束。模型纵向划分100份网格,网格纵向间距为2 m,变形缝及其附近网格有一定程度加密。由此建立的有限元模型和模型网格如图1所示。
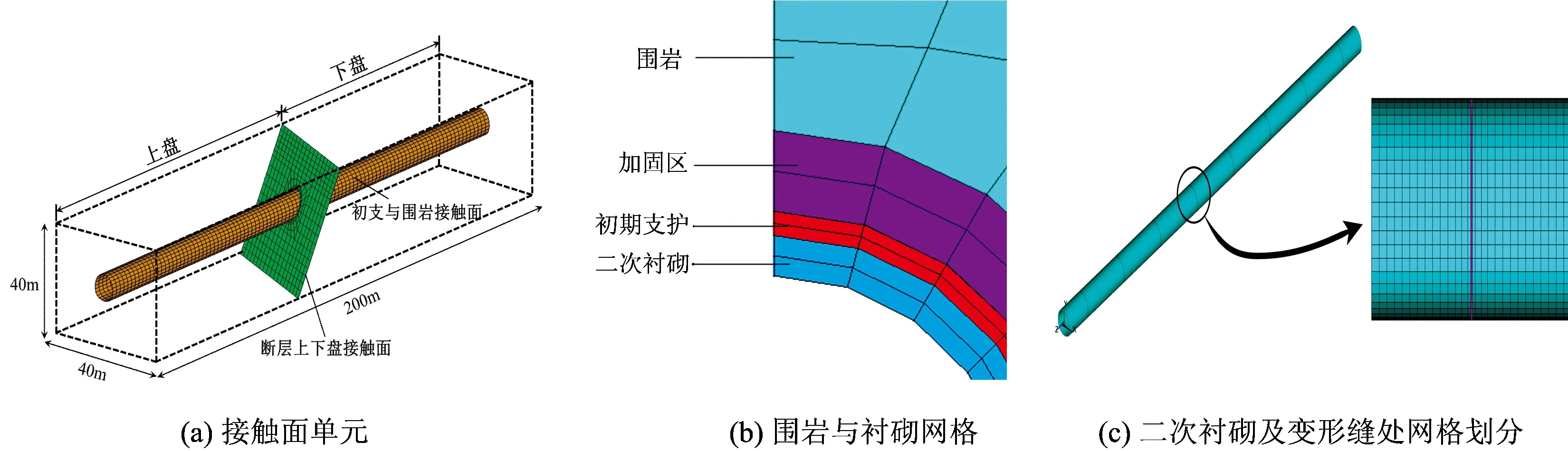
图1 有限元模型及网格划分
隧道采用复合式衬砌,图2为双接触面单元示意图,接触面采用扩展拉格朗日法计算,其中,接触面①为断层上下盘接触面,其接触行为设定为可滑动但不分离模式,以还原断层面上的错动力学行为;接触面②为初支与围岩接触面,其接触行为设定为可分离模式[13-14]。根据资料调研可知,断层错动后在断层面处的初支与围岩会发生脱空[15],因此采用可分离接触面还原脱空区隧道结构受力特征。
模型中围岩及衬砌参数根据乌鲁木齐轨道交通1号线地勘报告以及《铁路隧道设计规范》确定。考虑围岩加固措施的加固效果,提高了围岩的黏聚力和内摩擦角,加固区围岩的弹性模量、黏聚力按提高20%~30%考虑。不考虑水的作用。参考工程勘测资料并结合相关规范,各材料物理力学参数见表1,接触面模拟计算参数见表2。
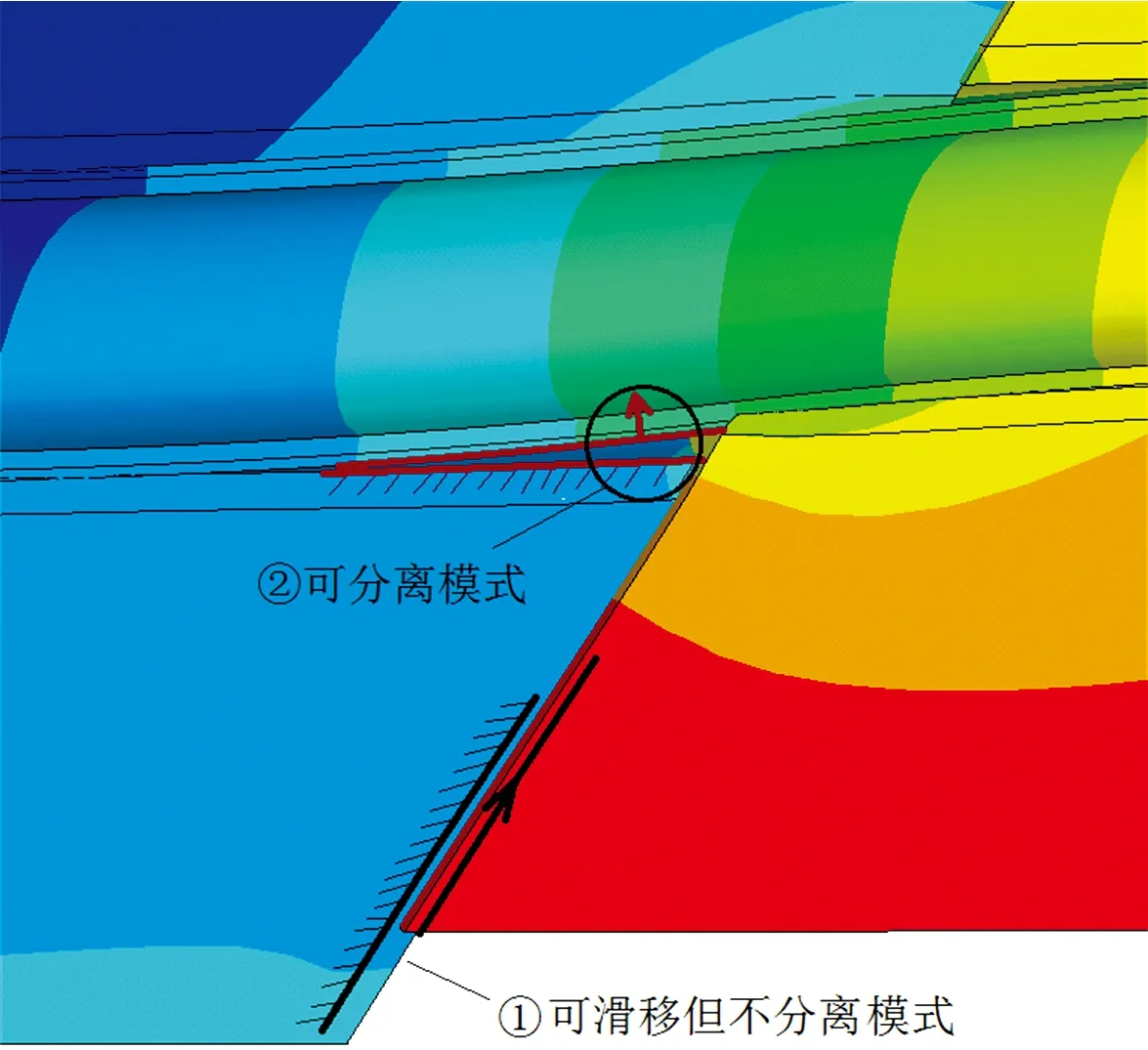
图2 双接触面工作模式图
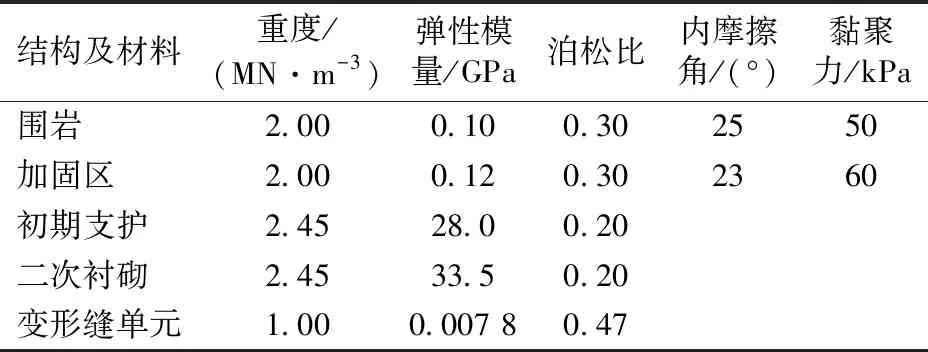
结构及材料重度/(MN·m-3)弹性模量/GPa泊松比内摩擦角/(°)黏聚力/kPa围岩 2.000.100.302550加固区 2.000.120.302360初期支护 2.4528.00.20二次衬砌 2.4533.50.20变形缝单元1.000.007 80.47
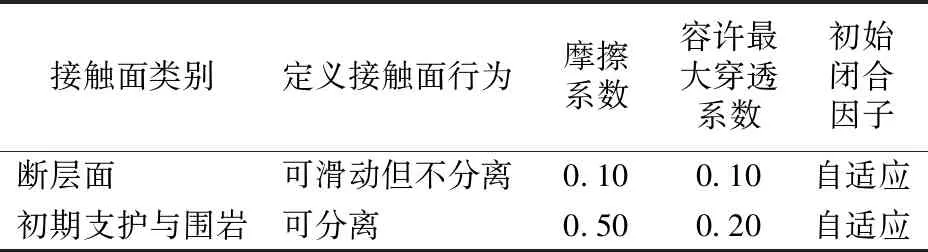
表2 接触面模拟计算参数
设置断层错动量(以下简称为错距)分别为10,20,30 cm,模拟分析3种错距下隧道衬砌的变形、受力及塑性区分布。
3 数值模拟结果
3.1 隧道衬砌变形及围岩压力
图3为错距30 cm时地层及隧道结构整体变形示意图,图4为不同错距时隧道衬砌变形放大图。由图3和图4可知:断层错动后,隧道衬砌沿着纵向发生了“S”状弯曲形变以适应错距;上盘仰拱近断层面处出现了明显脱空;下盘近断层面处拱顶与围岩也有脱空现象;随着断层错距的增大,脱空区范围也逐渐增大。

图3 错距30 cm时地层及隧道结构整体变形示意图
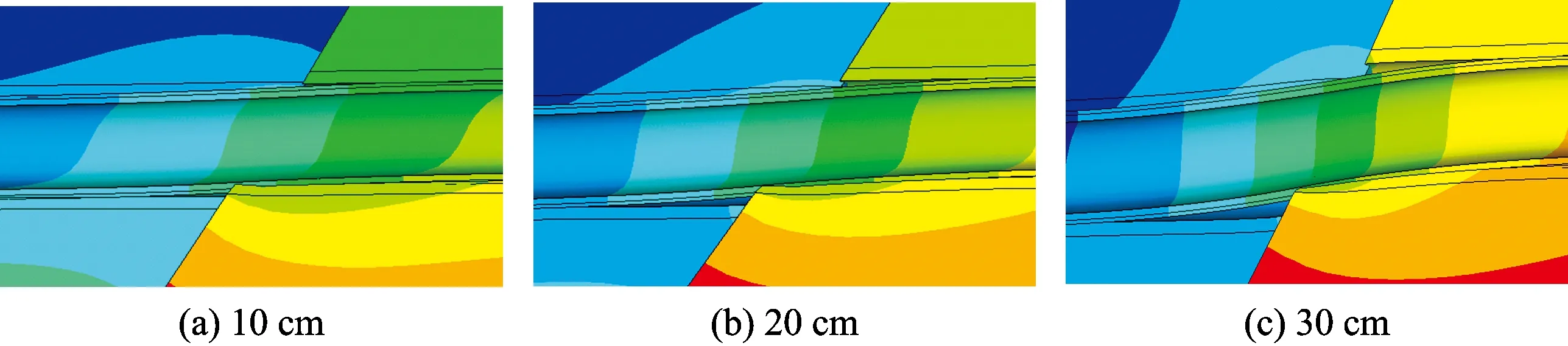
图4 不同错距下隧道衬砌变形放大图
图5为不同错距时二次衬砌竖向位移沿隧道纵向距离的分布曲线,图中,横坐标的纵向距离,以断层处为0点,往右侧下盘方向取正,往左侧上盘方向取负;纵坐标的竖向位移,以竖直向上为正,以竖直向下为负。由图5可知:随着错距增大,二次衬砌竖向位移逐渐增大;随着纵向距离的增加,二次衬砌竖向位移也逐渐增大,且以下盘的竖向位移最为明显。
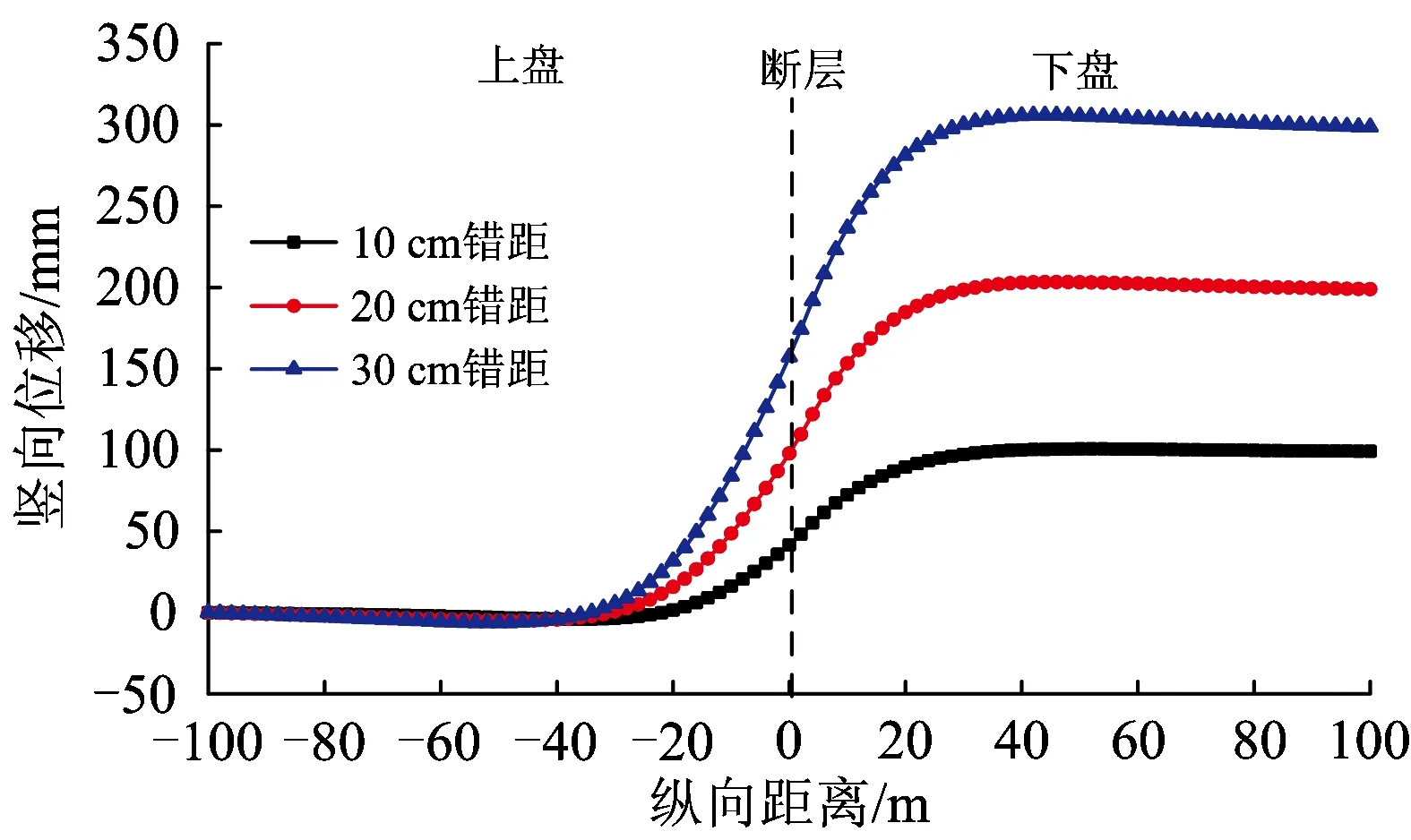
图5 不同错距时二次衬砌竖向位移沿隧道纵向距离的分布曲线
图6为不同错距时隧道拱顶、仰拱围岩压力沿隧道纵向距离的分布曲线。由图可知:断层面处围岩压力最大,且在上盘仰拱及下盘拱顶出现一段围岩压力为0的区域,即为脱空区;随着断层错距的增大,脱空区范围有所增大。但由于有限单元法采用连续介质假设,且实际城市浅埋地铁由于所处围岩条件差,隧道顶部围岩在自重作用下有发生塌落的可能,拱顶围岩最终可能只达到松散的程度,拱顶脱空并非必然出现。
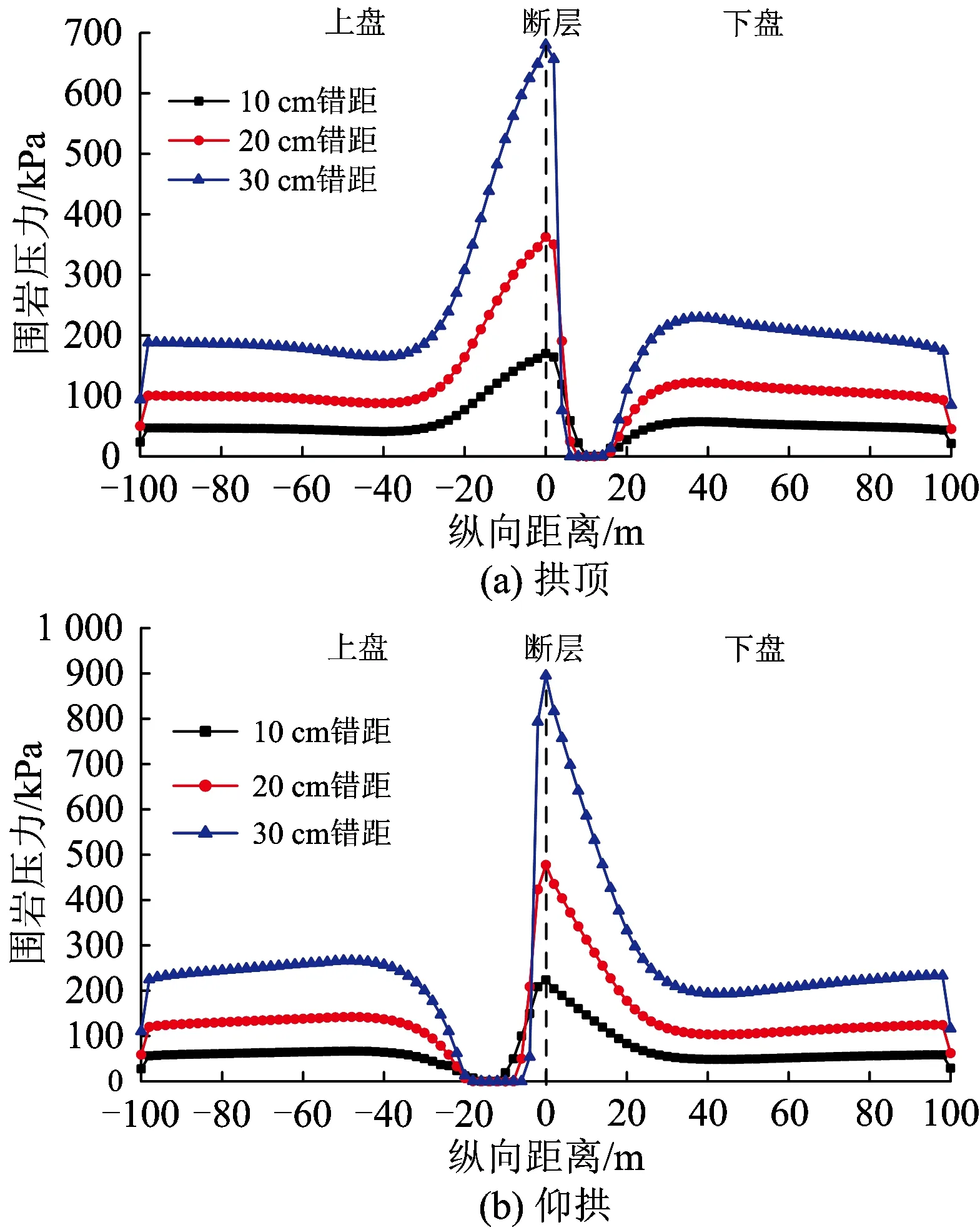
图6 不同错距时拱顶和仰拱处围岩压力沿隧道纵向距离的分布曲线
3.2 隧道二次衬砌应力
1)纵向应力
由于计算过程中考虑了二次衬砌开裂,开裂会导致应力释放,即开裂处纵向应力很小(接近0),该区域即为结构受拉开裂范围。
图7为不同错距时拱顶和仰拱处二次衬砌纵向应力沿隧道纵向距离的分布曲线,图中拉应力为正,压应力为负。由图可知,二次衬砌纵向应力具有反对称性质,即上盘仰拱、下盘拱顶靠近断层面处衬砌纵向应力为0,表明该区域衬砌混凝土受拉开裂;随着错距的逐渐增大,上盘仰拱和下盘拱顶处开裂范围逐渐增大,上盘拱顶及下盘仰拱处压应力也逐渐增大。
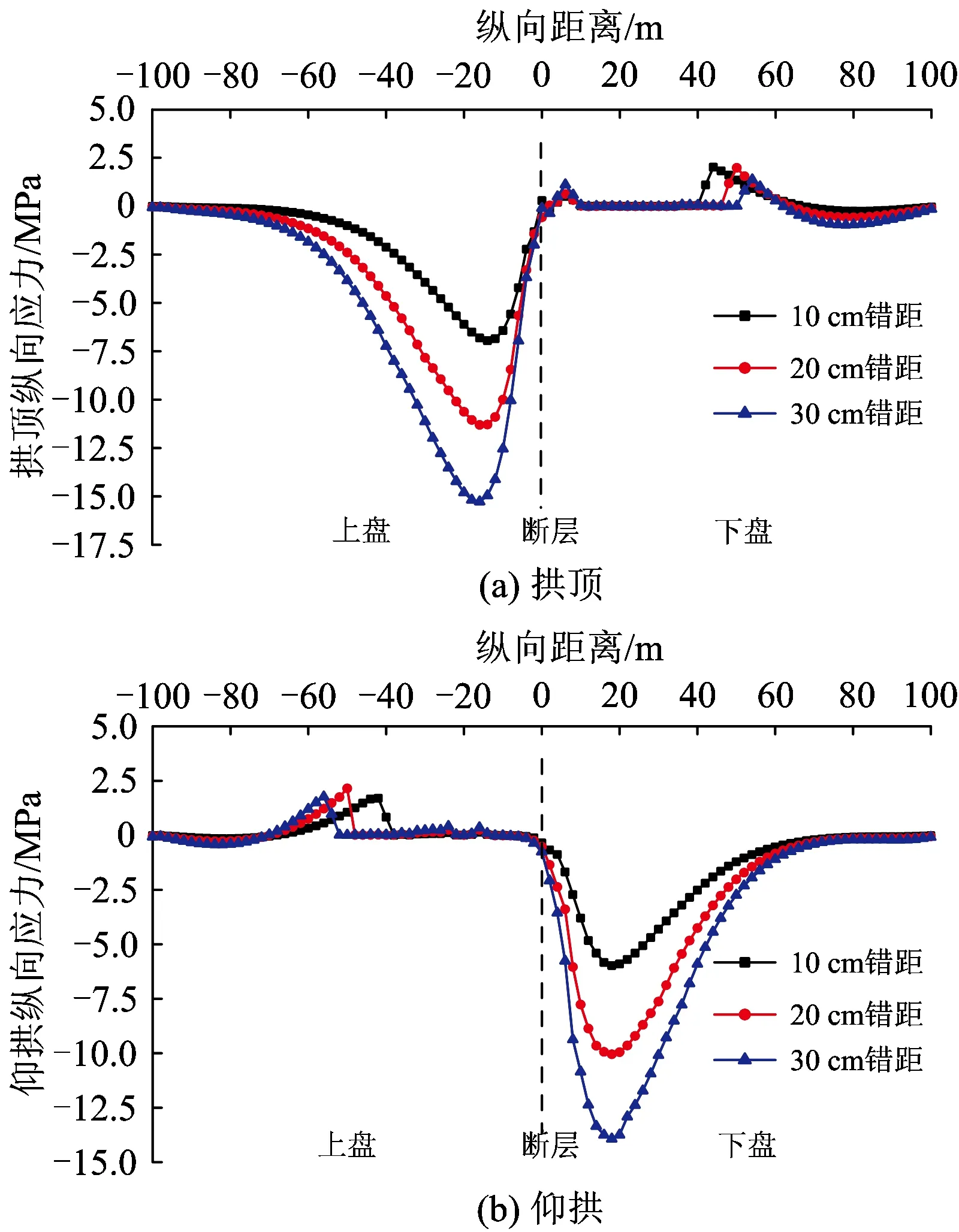
图7 不同错距时拱顶和仰拱处二次衬砌沿隧道纵向距离的纵向应力分布曲线
图8为不同错距时二次衬砌裂缝分布云图,表3为裂缝开裂长度表。由图8和表3可知:二次衬砌开裂范围随错距的增大而增大;当错距达到30 cm时,上盘仰拱开裂长度为52 m(6.9D),下盘拱顶开裂长度为40 m(5.4D),可见上盘二次衬砌开裂范围大于下盘。
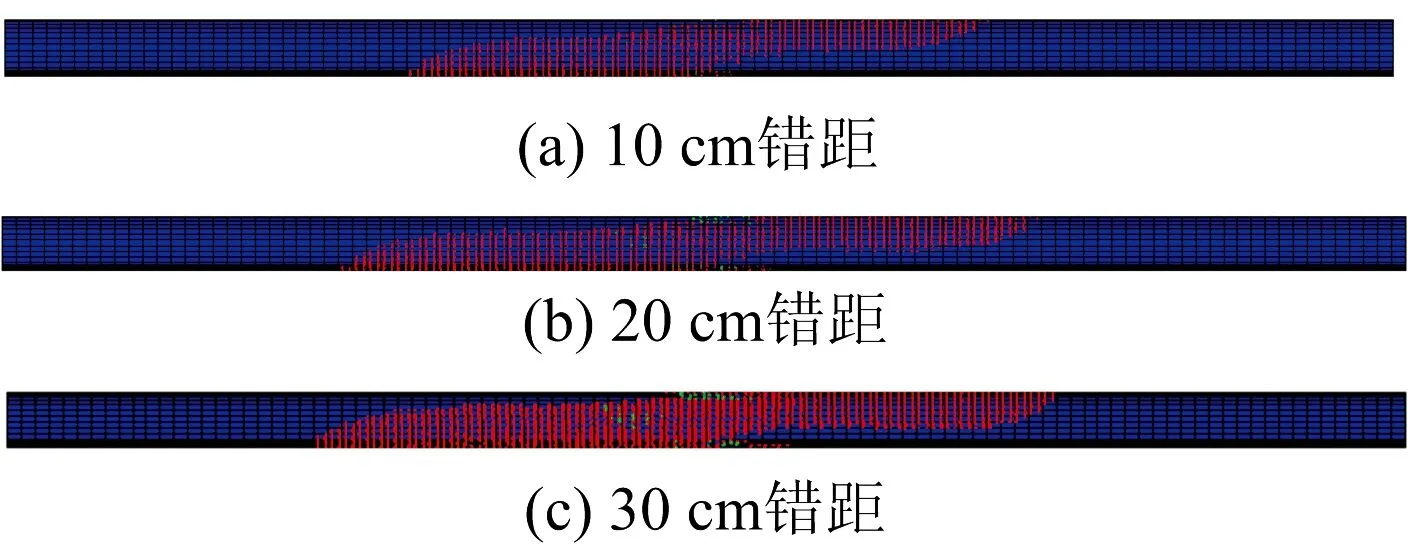
图8 不同错距时二次衬砌裂缝分布云图
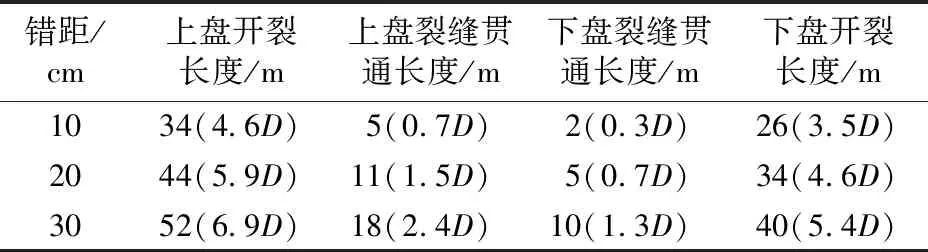
错距/cm上盘开裂长度/m上盘裂缝贯通长度/m下盘裂缝贯通长度/m下盘开裂长度/m1034(4.6D)5(0.7D)2(0.3D)26(3.5D)2044(5.9D)11(1.5D)5(0.7D)34(4.6D)3052(6.9D)18(2.4D)10(1.3D)40(5.4D)
2)最小主应力
图9为错距30 cm时二次衬砌最小主应力云图,由图可知,二次衬砌最小主应力峰值出现在断层面拱脚点。图10为不同错距时二次衬砌拱脚(右侧)沿隧道纵向距离最小主应力变化曲线,由图可知,拱脚处二次衬砌最小主应力在断层面处出现峰值,且在断层错动作用下,拱脚最小主应力随错距的增大而增大。

图9 错距30 cm时二次衬砌最小主应力云图
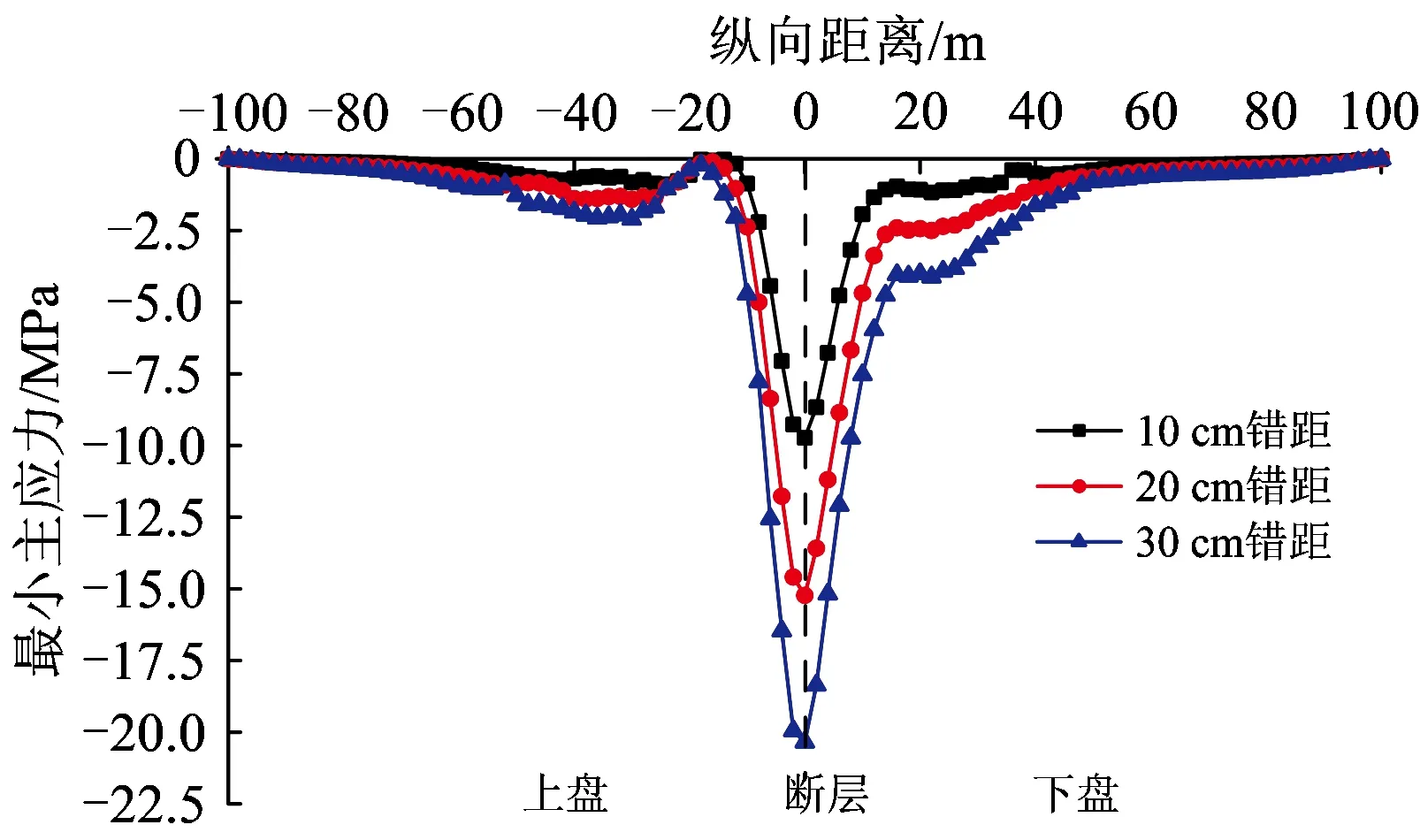
图10 不同错距时二次衬砌拱脚(右侧)最小主应力沿隧道纵向距离分布曲线
3)剪应力
图11为不同错距时隧道二次衬砌剪应力分布云图。由图可知,断层面处拱脚点衬砌剪应力最大。图12为不同错距时拱脚处二次衬砌最大剪应力沿隧道纵向距离分布曲线,由图可知,当断层错距分别为10,20,30 cm时,拱脚处最大剪应力分别为4.81,7.44,9.49 MPa,均大于C45标号混凝土抗剪强度设计值(2.8 MPa),极可能发生剪切破坏。
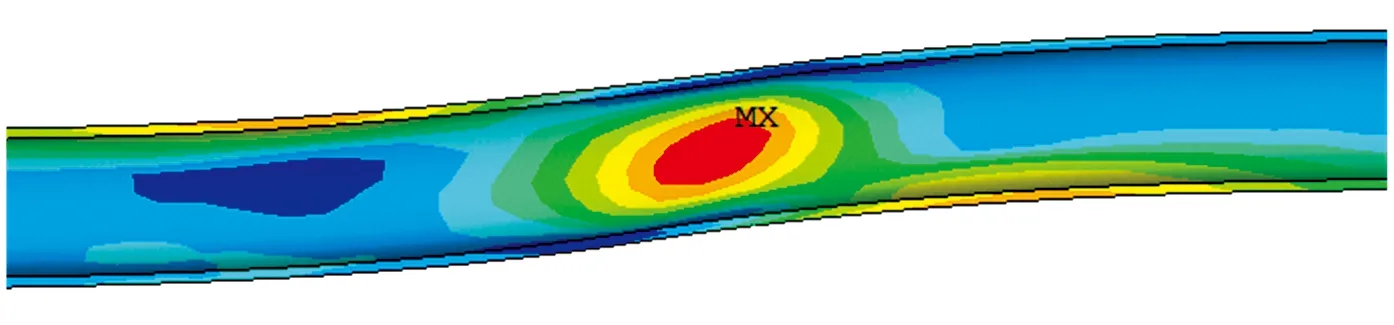
图11 错距30 cm时二次衬砌中剪应力分布云图

图12 不同错距时拱脚处二次衬砌剪应力沿隧道纵向距离分布曲线
3.3 隧道二次衬砌塑性应变分布
图13为不同错距时二次衬砌塑性应变分布云图,由图可知,上盘拱顶、下盘仰拱、断层面近拱脚区域均出现塑性应变,最大值出现在断层面处拱脚,峰值达到337×10-6。由隧道二次衬砌应力分析结果可知,上盘拱顶、下盘仰拱塑性应变是由于受压应力作用而产生的,断层面处隧道拱脚是由于受压应力、剪应力共同作用而产生的。
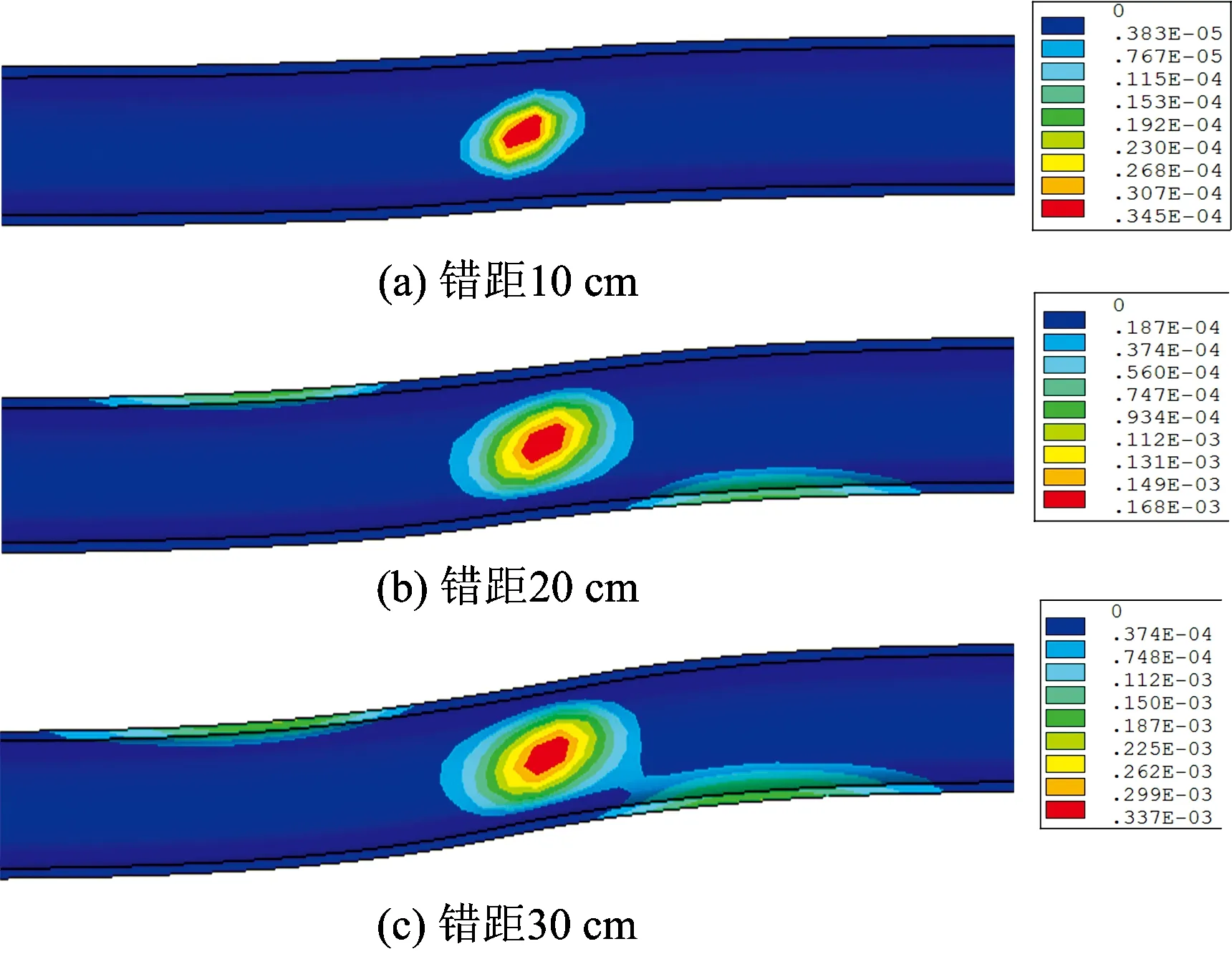
图13 不同错距时二次衬砌塑性应变云图
图14为不同错距时拱脚和仰拱处二次衬砌塑性应变沿隧道纵向距离分布曲线。由图可知:拱脚塑性应变最大,最大值出现在断层面附近,结合应力分析结果可知,此处塑性应变是受到压和剪共同作用产生的;拱顶塑性应变出现在上盘,仰拱塑性应变出现在下盘。
综上所述,断层错动作用下,在断层面处隧道二次衬砌承受拉、压、剪的组合作用,其破坏最为严重。
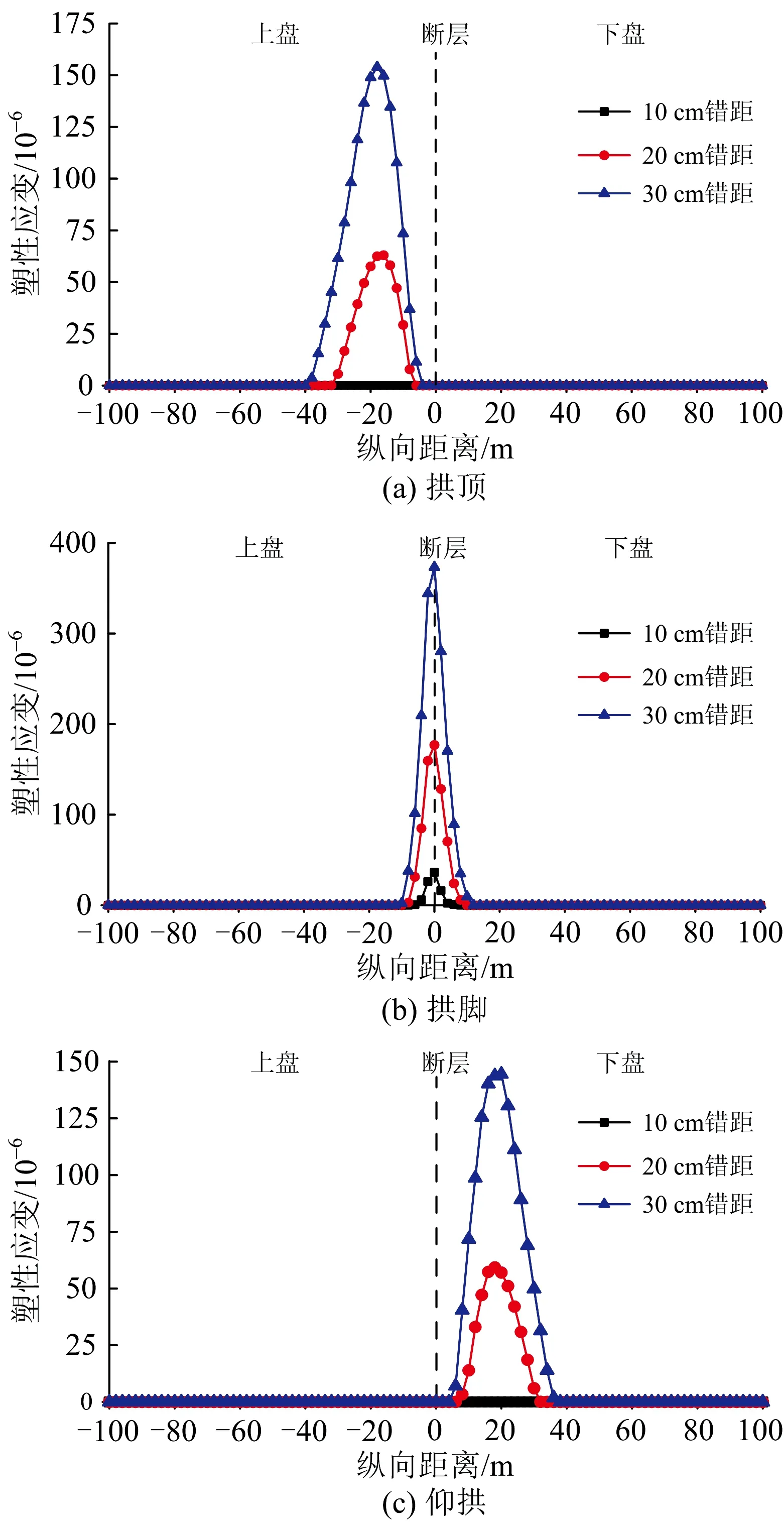
图14 不同错距时拱顶、拱脚和仰拱处二次衬砌塑性应变沿隧道纵向距离分臣曲线
4 大比例尺隧道穿越正断层剪切错动室内模型试验
4.1 试验装置
采用几何相似比为1∶25大比例尺的室内试验装置,进行隧道穿越活断层剪切错动试验。该试验装置如图15所示,主要包括装置箱体、加载装置、模型箱底座、数字伺服控制系统共4大部分。

图15 大比例尺隧道穿越活断层剪切错动试验装置
装置箱体的长×宽×高为5.0 m×2.5 m×2.5 m,箱体上设有60°剪切缝,左侧为正断层下盘,右侧为上盘。左侧下盘箱体的底板下安装有大功率丝杠加载装置,可沿设定角度的剪切缝向上错动,从而模拟正断层错动效果。加载速率设定为5 mm·min-1,加载目标错动量为12 mm,错动时间为144 s,相当于实际断层错动速率12.5 cm·min-1,总错距30 cm。
4.2 试验相似材料
取几何相似比CL=1∶25,重度相似比Cγ=1∶1。以此计算得到其他量的相似比分别为:弹性模量CE=1∶25;应力Cσ=1∶25;土压力CP=1∶25;泊松比Cμ=1∶1;应变Cε=1∶1;配筋量CAs=1∶625。
工程实际的围岩参数为:重度2 100 kN·m-3,弹性模量100 MPa,泊松比0.3,内摩擦角25°,黏聚力50 kPa。通过多次试验对比,确定围岩相似材料配比为河沙∶石英砂∶重晶石∶粉煤灰∶机油=40%∶30%∶10%∶10%∶10%。
石膏材料配比为水∶石膏∶硅藻土=1.0∶0.7∶0.3,其泊松比为0.194,弹性模量为1.3 GPa,单轴抗压强度为802 kPa。同时考虑钢筋的影响,在石膏模型中内置网格为1 cm×1 cm、直径为1 mm的方格钢筋网,然后进行石膏浇筑。由此制成隧道石膏模型长1 m,共做了5根,将5根纵向拼接制成总长5 m的隧道模型,从左至右顺序编号为1#,2#,3#,4#,5#段。
将相连接的2根隧道石膏模型间的缝隙用于模拟二次衬砌的变形缝,拼接时采用T型橡胶圈连接,T型橡胶圈按照实际工程止水带型式按相似比缩小后由同一工程供应商特别制作提供,性能参数见表4。二次衬砌变形缝的实际施工方案和试验模型如图16所示。

表4 试验用橡胶止水带材料性能参数
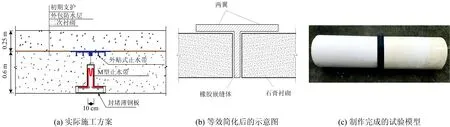
图16 二次衬砌变形缝的实际施工方案和试验模型
4.3 室内模型试验结果
随着左侧箱体(下盘)抬升错动,实时监测并记录隧道二次衬砌的竖向位移、纵向应变、环向应变及围岩压力,并对断层错动试验后的隧道衬砌裂缝特征进行分析研究。对试验数据进行整理分析,结果如下。
1)竖向位移
图17为不同错距时隧道二次衬砌拱顶竖向位移沿隧道纵向距离分布曲线。由图可知,随着错距的增大,下盘隧道结构逐渐抬升,上盘隧道垂直位移变化幅度很小。
图18为隧道二次衬砌竖向收敛位移沿隧道纵向距离分布曲线,竖向收敛位移表征的是隧道垂直方向的受压变形量。由图可知,断层面处竖向收敛位移最大,且随着错距增大而增大,表明断层面处隧道受断层上、下盘土体错动造成的竖向挤压作用最为明显。

图17 不同错距时隧道二次衬砌拱顶竖向位移沿隧道纵向距离分布曲线
2)纵向应变
图19为不同错距时拱顶和仰拱外侧纵向应变沿隧道纵向距离分布曲线。由图可知:随着错距的增大,下盘、上盘近断层处隧道拱顶外侧纵向应变均迅速增大,若以试验所得隧道模型衬砌材料极限拉应变106×10-6为破坏标准,则下盘距断层面-10~0 m范围内隧道拱顶纵向拉应变超限,上盘距断层面0~10 m范围内隧道仰拱纵向拉应变超限,超限区域将可能发生受拉破坏。
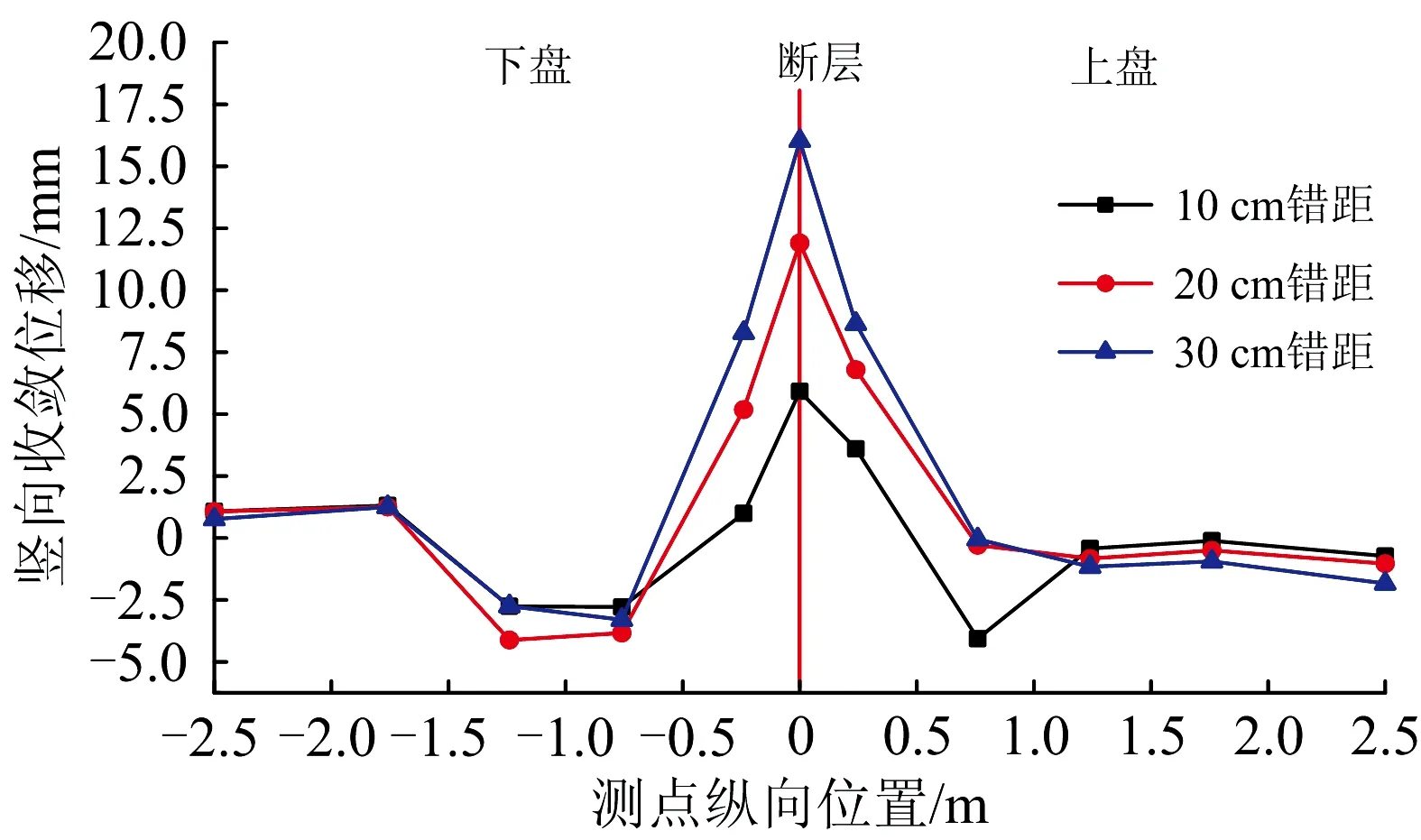
图18 不同错距时二次衬砌竖向收敛位移沿隧道纵向距离分布曲线
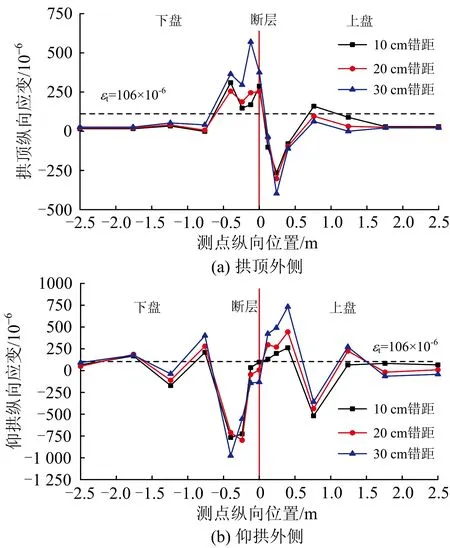
图19 不同错距时拱顶外侧、仰拱外侧二次衬砌纵向应变沿隧道纵向距离分布曲线
3)环向应变
图20为不同错距时拱顶和仰拱内侧环向应变沿隧道纵向距离分布曲线。由图可知:在断层面附近-10~10 m范围内,环向应变突然增大,在断层面处出现峰值并超过元器件量程而失去度数;在断层面附近-31~31 m范围内,仰拱环向应变也出现3次峰值。若以试验所得模型衬砌材料极限拉应变106×10-6为破坏标准,则峰值区域结构环向拉应变均超限。
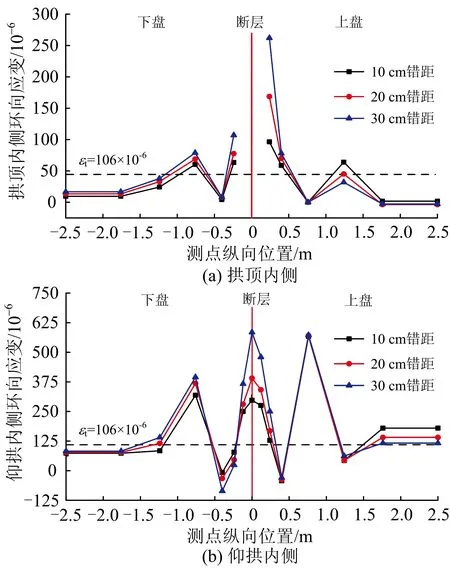
图20 不同错距时拱顶、仰拱内侧二次衬砌环向应变沿隧道纵向距离分布曲线
4)隧道拱顶与仰拱围岩压力分布
图21为不同错距时拱顶和仰拱围岩压力沿隧道纵向距离分布曲线。由图可知:拱顶围岩压力在断层面处出现突变,这是由于正断层错动作用下,上下盘地层与隧道之间的变形不同步造成的,因此在断层面附近的下盘拱顶和上盘仰拱出现围岩压力减小的区域,其中下盘仰拱脱空明显。
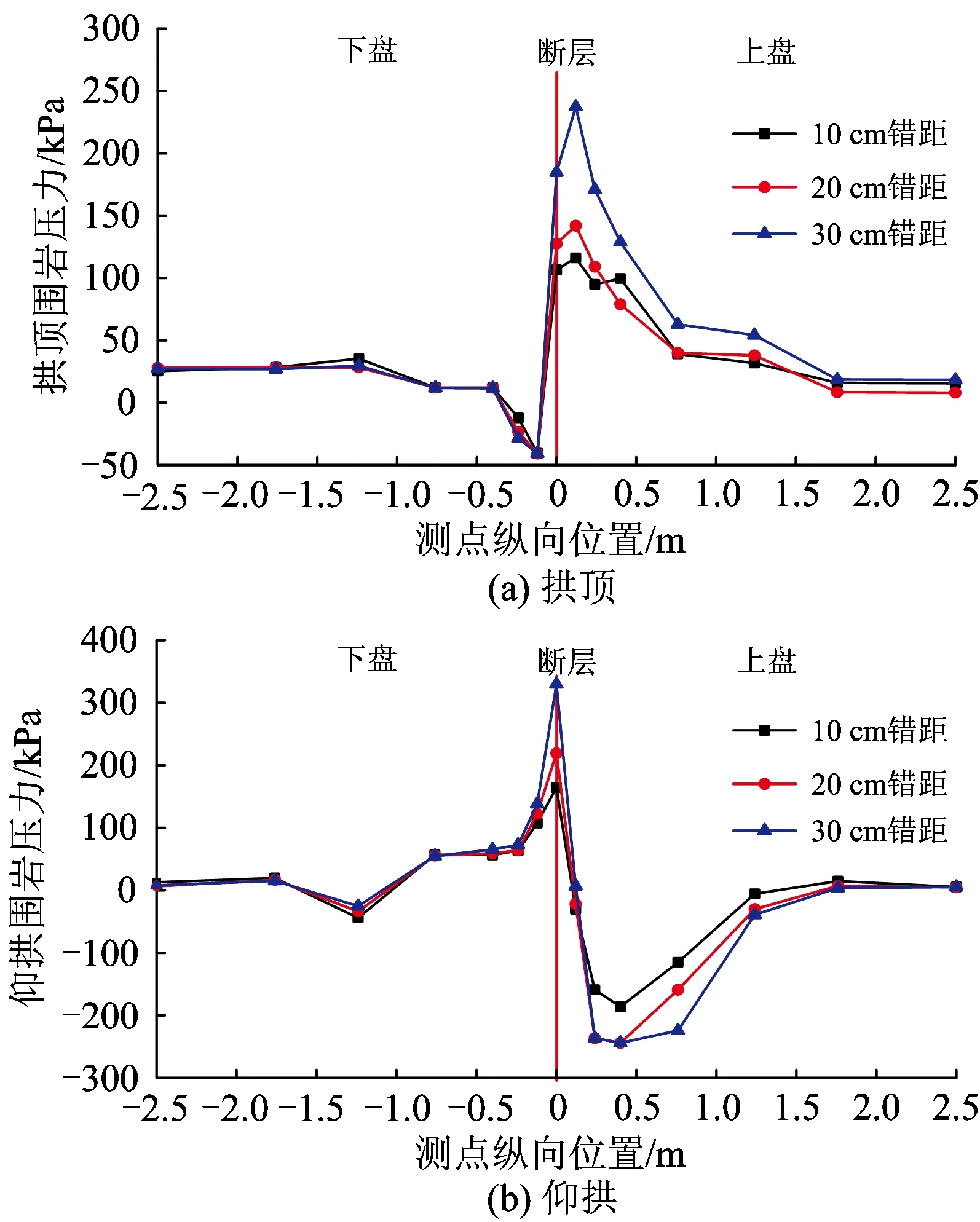
图21 不同错距时拱顶、仰拱围岩压力沿隧道纵向距离分布曲线
5)裂缝分析
图22为断层剪切错动试验后隧道模型开裂形态。从破坏范围、破坏程度、破坏特征上分析可得如下结论。

图22 隧道模型衬砌裂缝分布图
(1) 2#,3#,4#段均出现裂缝,其中,上盘隧道二次衬砌开裂范围约为125 cm(约为实际32 m,即4.3D),下盘隧道二次衬砌开裂范围约为88 cm(约为实际22 m,即3.1D),因此从开裂范围上看,上盘大于下盘。由于模型试验可还原实际隧道工程的结构特点,模型接头考虑了结构受迫时的能量释放等,而有限元数值模拟无法较全面地考虑隧道破坏过程中的能量损失和受力突变等,因此模型试验的结果准确性更高,而数值模拟的结果更偏保守,得到的二次衬砌开裂范围更大(见前文表3),但二者所得科学规律是一致的,即上盘二次衬砌开裂范围均大于下盘。
(2) 3#段由于直接受断层剪切错动作用,同时出现纵向裂缝、剪裂缝,且仰拱内侧纵向裂缝贯通整段,裂缝总长度约220 cm;上盘4#段隧道衬砌出现纵向裂缝、环向裂缝,全部为外侧裂缝,裂缝总长度约125 cm;下盘2#段隧道衬砌在仰拱内侧出现纵向裂缝,总长度约38 cm。因此从破坏程度上看:3#>4#>2#,即上盘大于下盘。
(3) 隧道二次衬砌开裂破坏主要以纵向裂缝为主,集中出现在仰拱内侧、墙脚外侧及拱顶内侧;剪裂缝出现在断层面迹线处的拱脚位置;环向裂缝多出现在拱腰位置。
(4) 针对隧道二次衬砌开裂以纵向开裂和斜向开裂为主的特征,提出采用“藕断丝连”的结构配筋设计理念,即加强环向主筋及箍筋,使隧道整体结构形成环—纵向骨架,从而减少纵向开裂和斜向开裂,并防止纵向裂缝的贯穿。
5 结 论
(1)数值模拟结果与模型试验结果的规律一致性较好。表现为:数值模拟围岩压力峰值位置与模型试验隧道二次衬砌纵向开裂位置一致;数值模拟隧道二次衬砌纵向应力峰值位置与模型试验隧道二次衬砌环向开裂位置一致;数值模拟结果与试验结果均有脱空现象出现且位置一致;数值模拟获得隧道二次衬砌裂缝数量及分布特征也与试验结果一致。
(2)正断层错动作用下,隧道衬砌受力复杂,表现为受拉、受压、受剪等状态。尤其在断层面处隧道衬砌承受了压—剪—扭的组合作用,衬砌破坏也最为严重。
(3)断层面处隧道二次衬砌开裂最为严重,开裂主要以纵向裂缝为主,集中出现在仰拱内侧、墙脚外侧及拱顶内侧;剪裂缝出现在断层面迹线处的拱脚位置;环向裂缝多出现在拱腰位置,上盘开裂范围均大于下盘。
(4)针对错动面附近隧道结构发生的极端破坏,提出采用“藕断丝连”结构配筋的设计理念,即加强环向主筋及箍筋,使隧道整体结构形成环—纵向骨架,从而减少纵向和斜向开裂,并防止纵向裂缝的贯穿。

