多列车限售策略和铁路票额预分方案的优化设计

张 琦，王 玉，李 华

(1.北京交通大学 交通运输学院，北京 100044； 2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044; 3.中国铁路上海局集团有限公司 客运部，上海 200071)

铁路票额预分的核心目标是基于对客流分布规律的把握，实现适应动态客流需求的票额分配，达到稳定常态客流，应对突发客流，吸引淡季客流，从而提高列车全程客座率及收益的目的。实际工作中广泛应用的模糊预分以客流情况对车站进行分组，各小组分别标记用途、设置限售以远站和共用范围，制定票额分配模板；然后将票额首先分给客流稳定的大站，其余车站通过共用、复用等策略分配票额。其中限售以远站的设置与解除，主要是保障长途旅客优先登乘长途列车的实际需求。不难发现，车站分组和限售以远站的设置必须充分考虑列车开行的停站经由、时刻、沿途站同方向列车开行情况及客流需求，影响因素十分复杂。然而目前实际操作中，则主要依赖铁路工作人员根据长期售票经验及路局和车站的相关规定完成。由于在具体执行过程中缺乏理论支撑，票额预分存在种种不合理的问题。比如预售前期票额管理过紧、预售后期票额管理过松；为保证票额的可控性，长途预留过多；限售区段设置过远等情况；这些问题在节假日客流需求波动时更为突出。同时，人工干预为主的控制方式在不同时期、不同客流需求条件下存在工作量繁琐的问题，更无法从全局角度优化考虑。

关于高速铁路票额预分的研究从客流与票额的相互关系角度可以大致划分出2种思路。第1种思路是客流和票额先后进行分配。史峰等[1]首先以最大旅客出行效用为目标将客流分配到各条线路、各列车上，然后对于单列车以最大运输人km确定限售站位置并进行票额的分配。第2种思路是直接以票额限制为决策变量构建数学规划模型，解决一定目标下的票额分配问题[2]。蓝伯雄等[3]将席位控制与发车时刻决策一起优化，能够解决多列车满足不同时间段的多种OD需求的多席位座位分配问题。第2种思路可以将旅客选择行为作为约束直接参与票额预分过程，方便解决联合优化的问题；还能够从全局最优的角度出发，同时对多列车的票额预分方案进行决策。

票额预分中，对相同OD提供旅客运输服务列车之间相互替代关系的表达是问题的关键。既有的针对多列车的票额分配策略主要从铁路线网的整体收益角度考虑票额的分配，重点在于多列车之间的选择和配合。赵翔等[2]重点考虑了多列车的停站方案对票额分配的影响。Luo等[4]在假设旅客对可达性相同的多列车有相同选择概率的基础上建立了多列车的票额分配模型。包云[5]研究了单一票价多列车、多等级票价多列车的票额分配问题，分析了不同情况下旅客需求的转移行为。宋晓芳[6]给出了存在限售站情况下的单列车票额分配模型，再建立相关多列车票额分配的优化模型。由于在考虑多列车替代关系时，不同车次的限售区段与限售时段将直接影响相关列车的服务情况和旅客在限售条件下的选择行为，而既有研究尚未能将限售方案的优化同步考虑，缺乏对限售条件下票额预分方法的讨论。

综上所述，为了提高不同客流条件下票额预分方案和限售策略的合理性与编制效率，填补现有研究在高铁限售情况下的票额预分方面的空缺，本研究结合旅客选择行为，分析限售策略对高速铁路多列车票额预分和旅客选择行为的影响，从而刻画在限售策略条件下多列车的OD服务替代关系，进一步构建以最大化运输人公里为目标的限售策略和票额预分模型，研究多列车的限售站位置、限售时间和票额预分方案的联合优化设计问题。

1 限售策略对多列车票额预分方案及旅客选择行为的影响

限售策略包括限售站位置决策和限售时间决策。对于限售站位置的设置和调整，铁路部门通常以“长途列车运送长途客流，短途列车运送短途客流”为原则确定限售以远站。限售时间决策是指限售解除(简称解限)时间的决策。解限的一般原则为：从旅客列车客座率角度而言，列车客座率越高，限售解除时间应该越接近列车开车时间，使长途旅客有充分的购票时间，列车客座率越低，限售解除时间应越早，目的是用短途旅客的需求提高列车客座率；从旅客购票行为角度而言，对于大部分旅客习惯提前购票的列车，解除限售的时间应相对提前，对于大部分旅客习惯就近购票的列车，解除限售的时间应相对靠后[7]。

1.1 限售策略对多列车票额预分方案的影响

限售策略对多列车票额预分的影响可以用下面的例子简单说明。假设1条高速铁路线路上有A，B，C和D这4个车站，列车1和列车2为从A到D的长途列车，列车3为从A到C的短途列车，列车定员均为500人。在预售期(假设为5天)内每天的旅客购票需求量见表1。

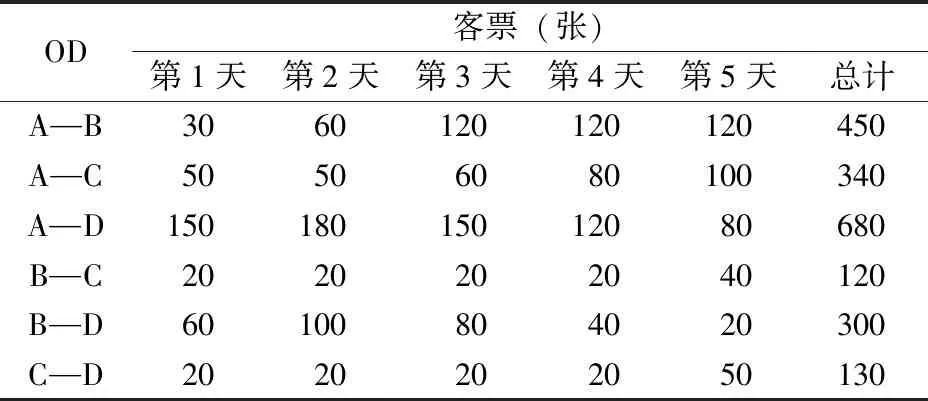
表1 预售期每天旅客购票需求量

假设列车1受限售控制，在预售期第1天至第3天限售至D站，第4天起解除限售；列车2和列车3不受限售控制；暂时排除对旅客选择行为的考虑，认为相同OD之间旅客选择各列车的概率相等，例如对于第4天A到C的80个需求，倘若列车1此时限售已解除且所有列车均能力充足，则列车1和列车3分别为A到C的旅客提供40张票额。

根据客票发售先到先得、同一天的需求中优先满足长途的原则，限售解除前后票额预分结果如图1所示。限售解除前列车1只服务到达限售站以远的客流，解除后也服务沿途短途客流。对比限售控制下的票额预分方案和无限售控制下的方案，如图2所示。由图1和图2不难看出：由于客票发售遵循先到先得的原则，无限售控制时，列车1承担了更多的短途客流，短途客流分配的票额多于限售控制下的短途票额，先到达的短途需求占用了列车部分载客能力，使得后续长途客流(如A到D，B到D)的票额较少；而在限售控制下，由于限售策略为长途需求保留了部分的列车载客能力，因此列车1承担了更多的长途客流，并将部分短途客流转移到了列车2上，使更多长途客流的需求得到了满足。比较2种情况下未被满足的购票需求，见表2。

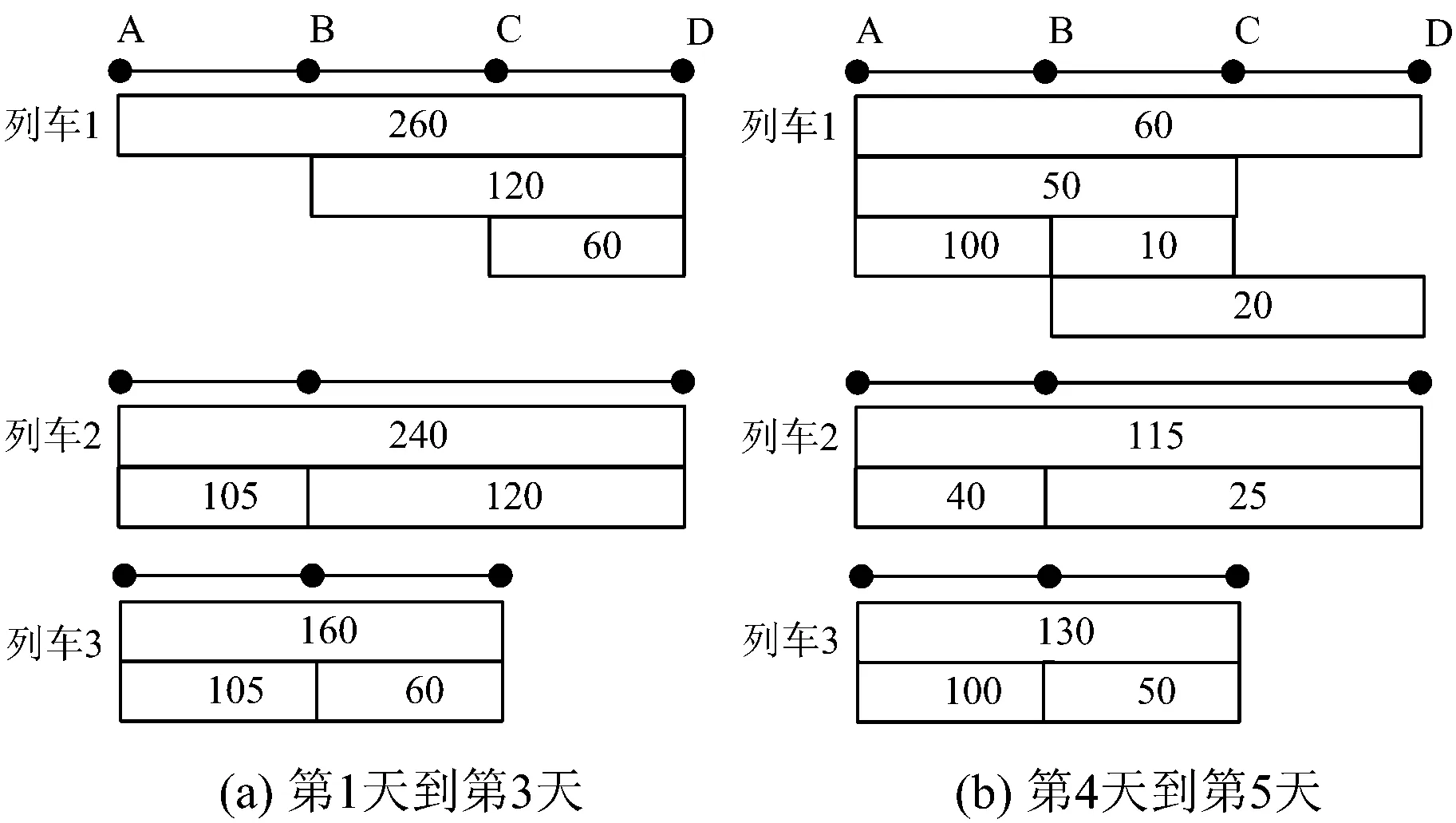
图1 限售解除前(第1～3天)后(第4～5天)的票额预分方案(单位：张)

由表2可知，有限售和无限售条件下，未被满足的购票需求总量是相等的，但是有限售的票额预分方案中长途需求的未满足量明显较少，说明限售方案在总体上也能够给予长途客流一定的优先。

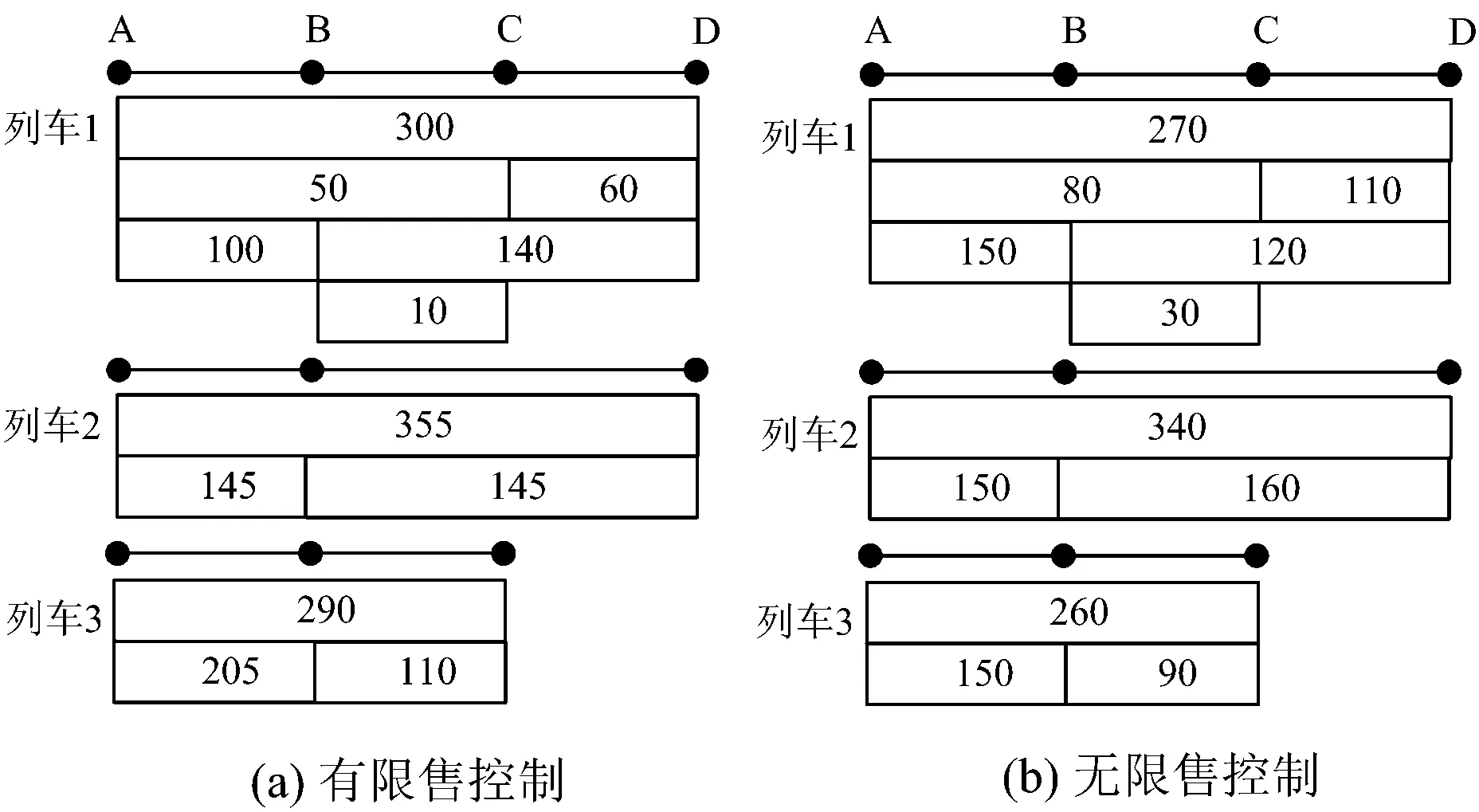
图2 有限售和无限售控制下的票额预分方案(单位：张)

表2 有限售和无限售时未被满足的购票需求量

1.2 限售策略对旅客选择行为的影响

限售对旅客在多列车之间选择行为的影响同样以图1、图2中的列车进行说明。假设对于从A到B的同种类型旅客，在3趟列车的票价、时间都相等的情况下，无限售控制时乘客选择3列车的概率均为1/3；如果旅客在购票时发现列车1只出售终到C站或D站的车票、不能提供A到B的服务，则旅客将只在列车2和列车3之间做出选择，概率分别为1/2。在考虑旅客选择行为的情况下，分配的票额也必须相应做出调整。

由此可见，在不考虑旅客到达站分布的情况下，限售策略的执行，使得部分旅客可选择的列车集合规模变小，导致旅客选择各列车的概率不同于无限售的情况。可见限售策略通过改变可供旅客选择的列车集合，显著影响了旅客选择各列车的概率。

2 多列车限售策略和票额预分模型

同时考虑限售策略和票额预分问题直接相关的旅客行为包括2个方面：一是相同OD旅客对不同列车的选择行为，根据第1节的分析，这一选择行为会影响提供相同OD服务的多列车的票额预分结果；二是旅客在预售期内的提前购票行为，它反映长短途、或不同OD之间旅客在购票时间上的偏好与解限时间密切相关。例如，当大部分长途旅客均提前至少20天买票时，为了充分利用剩余的短途席位，解限时间设在距发车日20天左右为宜；而当长途旅客大部分购票较晚时，解限的时间需要相应滞后，以便为晚到的长途需求保留席位。在实际情况中，长短途客流往往交织到达，解限时间将不能简单地通过售票经验判断得出。

2.1 旅客选择行为的描述方法

旅客选择行为包括旅客在预售期的提前购票行为(实质是旅客对购票日期的选择)和在多列车之间的选择行为。为了对旅客选择行为进行表达，定义2个概率，即旅客在预售期内每日购票的概率和旅客对不同列车的选择概率，分别描述旅客在预售期的提前购票行为和在多列车之间的选择行为。

旅客购票需求到达规律的描述方法包括非齐次泊松过程的仿真方法[8]、客流预测法[9]、出行效益公式法[10]、购票请求概率模型[11]等。这些方法大都离不开对历史购票数据的统计分析[12]，本文对此不展开详细研究，选择将旅客购票需求的到达规律表达为各OD间的旅客在预售期内每日购票的概率。

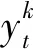
(1)

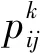
式(1)中0-1变量的引入，保证了对于实行限售的列车，在实行限售期间，只有限售站以远的车站才能分配票额，在限售解除期间限售站以近和以远站都可以分配票额，即属于限售解除期、限售站以远站这2个条件中的任何1个得到满足，旅客才能够选择该列车，效用函数才有效。

(2)

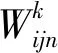
这样，在已知总OD客流需求的条件下，可以通过旅客在预售期每日的购票概率得到每日的OD客流需求，进而通过不同旅客对不同列车的选择概率(式(2))得到每列车在每日和每对OD之间的客流需求。

2.2 多列车限售策略和票额预分模型

多列车限售策略和票额预分模型就是对多列车解除限售的时间点、各列车限售站的位置和各列车、各OD之间分配的票额进行求解的模型。

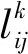
由于票价率递远递减，以最大化客票收益为目标必然会牺牲长途旅客的利益，与限售策略尽可能满足长途旅客需求的目的相悖。因此，以列车输送的最大人公里为优化目标，以列车输送能力、旅客需求、限售执行和限售解除等为约束条件，建立多列车限售策略和票额预分模型为

(3)

s.t.

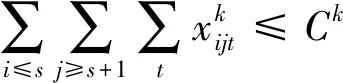
(4)

(5)

(6)

(7)

约束条件中：式(4)表示在该线路的每个区间内，每一列车所分配的票额均不能大于其能力；式(5)表示所分配的票额受该OD之间该列车的各类旅客的总需求约束；式(6)表示列车k一旦解除限售就将保持票额放开的状态直到发车；式(7)表示列车k的限售区段是连续的。

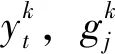
3 算 例

以上海虹桥站—广州南站的线路区段为背景，列车1，2，3，4为服务于这条线路的4趟列车，其停站分布如图3所示。各列车在各OD之间的票价、距离和旅行时间均参考实际线路的情况。对列车1和列车2采取限售措施。

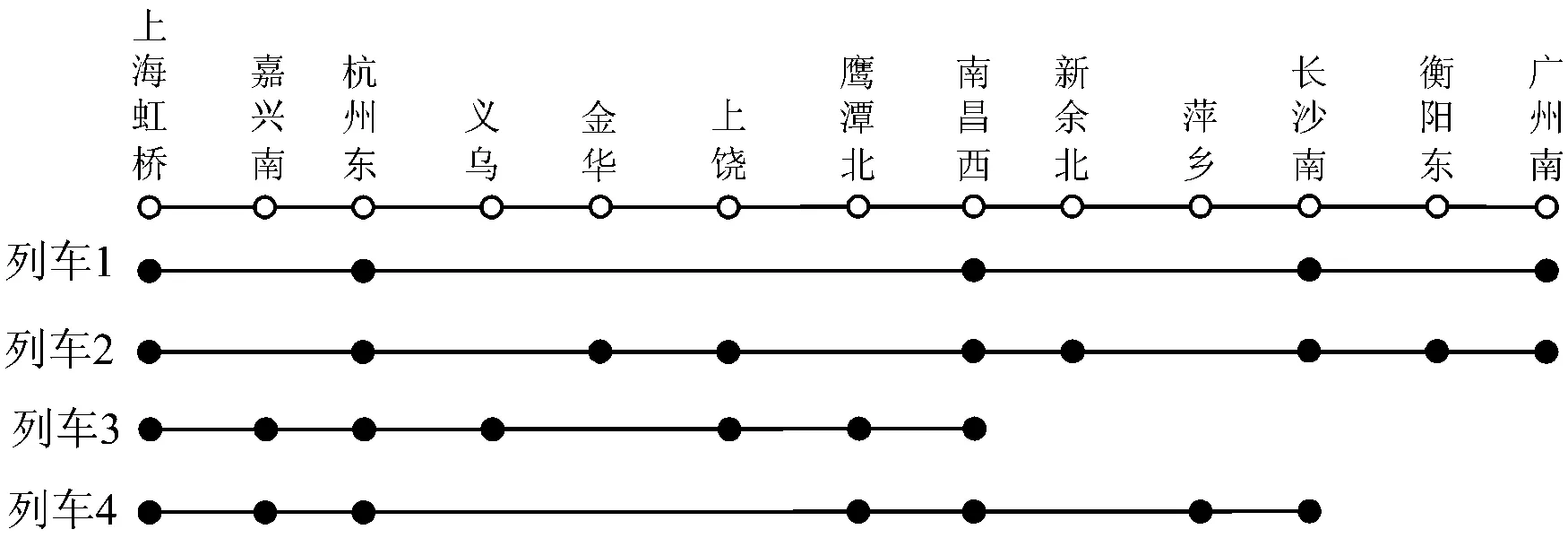
图3 上海虹桥—广州南线路区段4趟列车停站示意图

旅客对各列车的选择采用随机效用理论表达，根据问卷调查将旅客划分成5类，并对各类旅客的价格敏感度和时间敏感度参数进行标定，见表3；通过公式(2)计算旅客对各列车的选择概率。旅客提前购票天数的表达由于缺乏真实数据，因此按照一般长途需求更倾向于提前购票的规律，对长短途旅客在预售期(30天)内每日的到达概率进行了假定，其中，长途旅客的购票高峰出现在第10天，约占全部长途客流需求的6.6%；短途旅客的购票高峰在第20天，约占全部短途客流需求的6.7%。

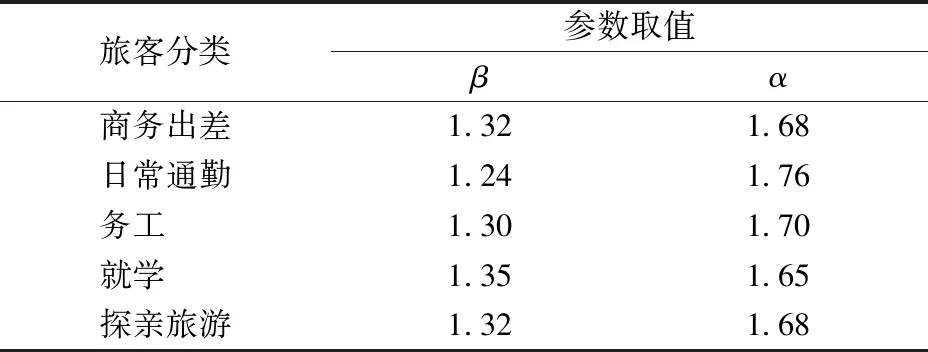
表3 不同类别旅客的价格敏感度和时间敏感度参数

模型求解得到：列车1的限售方案为第1～第17天限售至长沙南站以远，第18天全部放开；列车2的限售方案为第1～第29天限售至新余北站以远，最后1天全部放开；4列车票额预分结果如图4所示；4列车总输送人公里为3 178 455 人km，总客票收益为137.178 3万元。

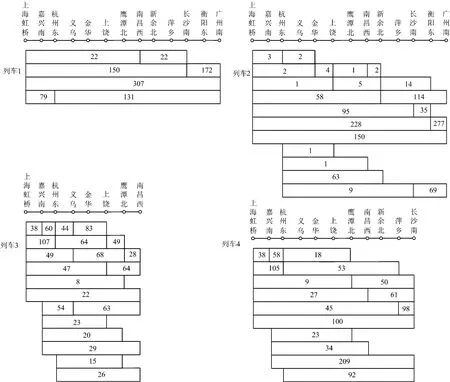
图4 各列车票额预分方案

同样对该算例，以传统的限售站决策方法求解作为对比方案。首先以旅客总出行成本最小为目标将各OD的客流分配到各列车上，再以最大化人公里为目标确定限售站位置，最后在客流分配结果和限售站位置的基础上，以尽可能满足长途旅客需求为原则进行票额预分；采用Lingo进行求解。求解得到：列车1的限售站为广州南，列车2的限售站为长沙南；各列车票额预分方案如图5所示，4列车总输送人公里为2 895 941人km，总客票收入为126.002 7万元。可见传统方法所得方案在输送人公里和客票收入上都明显少于本文的模型方案。

比较2种方案的客座率(各区段客座率的平均值)，见表4，可见除列车1以外，模型方案其余3列车的客座率均明显高于对比方案。这是由于模型从全局的角度考虑，同时协调了长短途客流之间、各列车之间的关系，让长途列车在满足一定长途客流的基础上有选择地承担了部分短途客流，使短途列车的区段能力得到了更充分地利用，说明本文模型生成的票额预分方案能更好地协调多列车所承担的客流关系，达到整体优化的效果。另外，本文的方法可以对限售解除时间进行预判，而传统方法只能决定限售站位置，解限时间需要凭借售票过程中的人工经验进行判断。

表4 2种票额预分方案的客座率

在实际应用中，可利用本文模型，根据实际条件，调整模型的输入，例如各OD的需求量、旅客提前购票时间的规律等，求解出相应的限售策略和票额预分方案。可见，在对客流规律准确把握的前提下，本文模型所得到的结果能够为限售策略的制定和票额预分及其优化提供参考和理论支持。

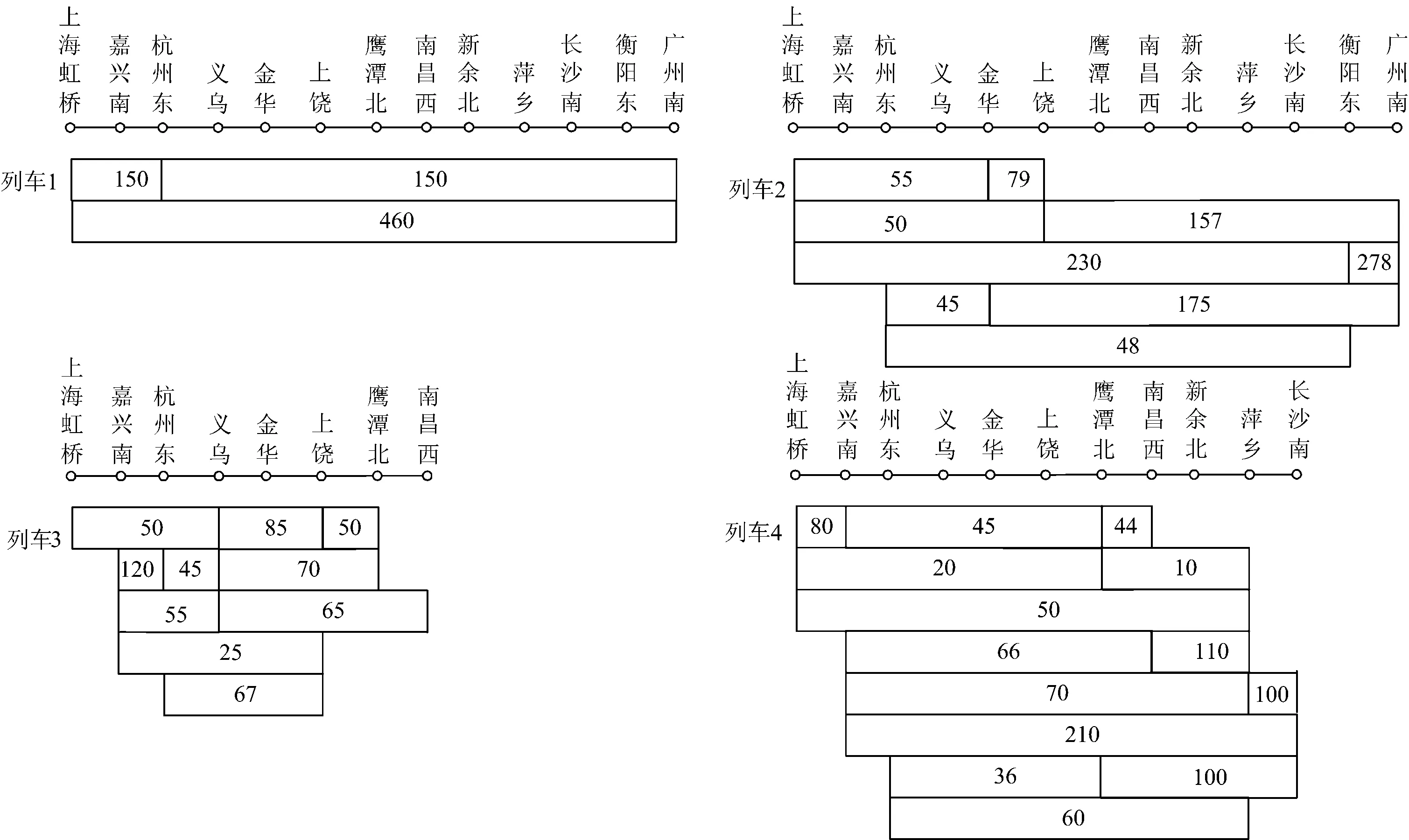
图5 传统限售站决策方法得到的票额预分方案

4 结 语

本文针对目前铁路客票限售方案过度依靠人工经验进行决策的问题，提出了利用数学模型对限售站、限售解除时间和相应的票额预分方案进行联合优化的方法。本文构建的模型支持对旅客提前购票行为与多列车选择行为的有效反映。在进一步的研究中，可以通过历史数据挖掘或调研等途径，提高不同旅客的价格和时间敏感度参数的准确度，并对预售期内的需求到达规律提出更符合实际情况的描述方法。