穿越分层地层的盾构隧道开挖面稳定机理研究
邱 龑, 杨新安, 黄德中, 徐前卫
(1.上海隧道工程有限公司,上海 200232; 2.同济大学 道路与交通工程教育部重点实验室,上海 201804; 3.同济大学 交通运输工程学院,上海 201804)
珠三角地区的地层为软硬不均地层,在采用盾构法修建城市地铁隧道时,常遇到岩性变化较大的地层,其中以上软下硬现象居多,致使盾构开挖面稳定难以控制。而盾构施工中一旦出现开挖面失稳,会不可避免地导致地表产生过大的变形,进而使地面建筑物或路面出现不可控的破坏,造成巨大损失。
为了研究确保开挖面稳定的支护压力上下限,基于塑性力学上限定理的极限分析方法被引入到开挖面稳定性分析中。Broms & Benermark[1]研究了黏性土不排水条件下的开挖面稳定性问题,并提出了开挖面稳定系数的概念。Davis[2]基于此概念,提出了圆柱体和球形体的破坏模型,利用塑性极限分析上限法研究了开挖面坍塌和隆起的破坏机理。Leca-Dormieux[3]提出用1个或2个圆锥形块体圆弧滑动的上限解,还将理论计算结果与Chambon[4]离心机试验得到结果进行了对比,发现二者具有较好的一致性。A. H. Soubra[5-7]先后提出数种多块体模型,其破坏面更加平滑,且得到的数值结果也比前人模型的分析结果要好。G. Mollon[8-10]进一步优化了多圆锥形块体模型,同样提出了数个不同的上限解。Subrin & Wong[11]提出了一种三维旋转坍塌破坏模型,该模型的破坏面完全由对数螺旋线表达,与之前的理论结果相比,其结果更优。国内许多学者[12-23]也相继对盾构开挖面稳定性问题提出了自己的研究成果。
通过对前人成果的研究发现,塑性极限分析理论的失稳模型在盾构隧道圆形断面上均为内切椭圆,没有包括整个圆形开挖面区域,且极少提及穿越软硬不均地层时的上限解。受限于塑性极限分析理论基本假定,计算支护压力为均布力,使得极限分析仅适用于压气法盾构隧道。
本文以穿越分层地层土压平衡盾构为研究对象,利用塑性理论极限分析上限法,基于空间离散化技术,生成穿越分层地层的盾构开挖面三维破坏机构,进而确定极限支护压力,为盾构设计和施工过程中合理控制开挖面支护压力提供理论依据,以期保证盾构在施工过程中的安全性与可靠性。
1 速度场的建立
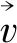
图1 盾构隧道螺旋破坏模式在平面YZ的断面图
3条对数螺旋线的极坐标表达式分别为
r1=rAexp[(β-βA)tanφu]
(1)
r2=rIexp[(βI-β)tanφu]
(2)
r3=rBexp[(βB-β)tanφd]
(3)
其中,
(4)
(5)
(6)
(7)
(8)
(9)
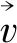
(10)
(11)
由于点F是起始于A和I两点的2条对数螺旋线的交点,所以F点的极坐标rF和βF的表达式为
(12)
rF=rAexp[(βA-βF)tanφ]
=rBexp[(βF-βB)tanφ]
(13)
其中由式(13)可进一步求得rF,即
(14)
而I点的极坐标rI和βI则可由牛顿解方程法求得。
2 三维破坏机构的逐点生成
2.1 离散化原则

(15)
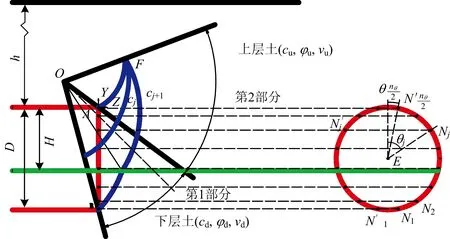
图2 破坏机构离散示意图

(16)
(17)

在第1部分和第2部分中的每个径向平面中,分别建立局部坐标系Cjxjyj,其中,Cj为平面Πj与以O为圆心、以rF为半径的圆的交点。注意到yj指向O点,xj与X轴同向。点Cj在XYZ坐标系中的坐标为
(18)

图3 隧道开挖面上离散点在局部坐标系下的角度

(19)
其中,

(ZCj-ZNj)sinβj
(20)
(21)
2.2 速度场的生成
如图4和图5所示,破坏机构面上离散出的任一点均可由Pi,j表示,其中,下标i表示该点是其所在径向平面的上第几个点,下标j表示该点处于第几个平面。通过已知平面Πj上2个点Pi,j和Pi+1,j
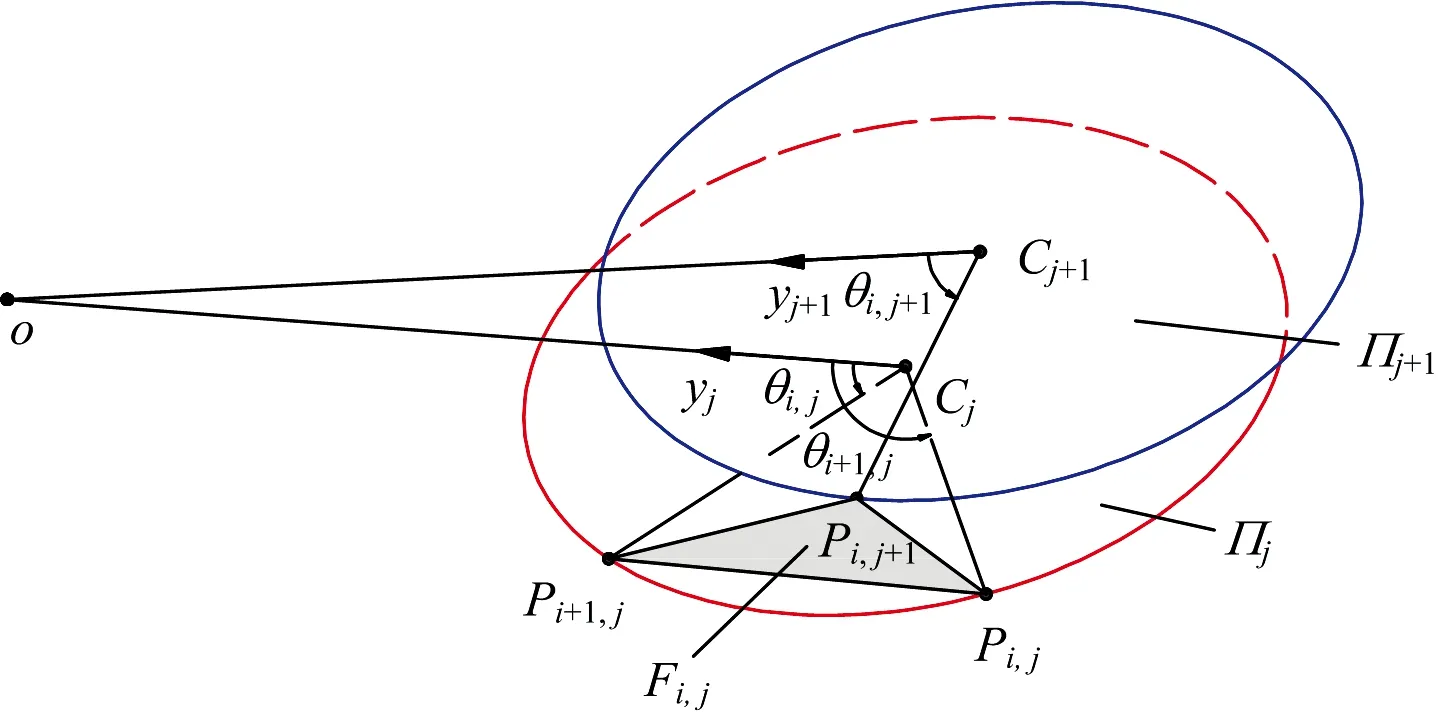
图4 由Pi,j和Pi,j+1生成Pi+1,j示意图

图5 Πj和Πj+1平面图
的坐标计算生成平面Πj+1上任一新点Pi,j+1的坐标。
1) 第1部分中新点的生成方法
(22)
(23)

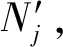
2) 第2部分中新点的生成方法
3) 由已知2个点生成1个新点的数学表达式

(24)

(25)

(26)
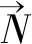
(27)
(28)

(29)

(30)
Xnax+Ynay+Znaz=0
(31)
(32)
需要注意的是,式(30)中的φ为地层的内摩擦角,计算过程中,以图2中的βI为界,当任一角βJ小于βI时,φ取下层土的内摩擦角φd,反之,φ取上层土的内摩擦角φu。
为了得到平面Πj+1上点Pi,j+1的位置,可得
(33)
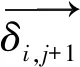
(34)
为获得点Pi,j+1的坐标,采用下列计算:
(35)
其中,

(36)
可以推导出ri,j+1的表达式为
(37)
最终,得出点Pi,j+1在XYZ坐标系中的坐标为
(38)
各点位置与破坏机构线之间的位置关系如图6所示。

图6 各点位置关系
2.3 生成破坏机构
速度场的生成在满足以下2个条件其中之一时终止:①从图1和图2中可清晰地看出,F点为速度场的收敛点,所以最新生成的夹角βj+1≤βF;②生成的ri,j+1<0,同样由图6可知,第1部分新生成的平面Πj+1面积应小于平面Πj,如果ri,j+1≥0,会出现平面Πj+1面积大于平面Πj面积,进而导致速度场不收敛。
通过上述“逐点生成法”,可生成图7所示的破坏机构,其中2种不同地层在竖直方向上各占开挖断面的一半。
3 开挖面极限支护压力的计算方法


图7 破坏机构
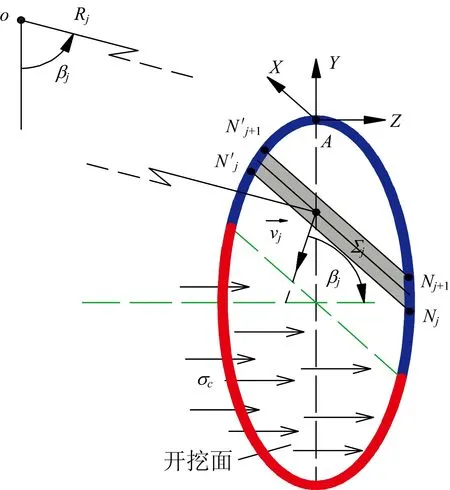
图8 开挖面支护压力做功示意图
根据图8和图9,极限支护压力做功功率为
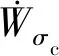

(39)
土体自重做功功率为
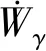
(40)
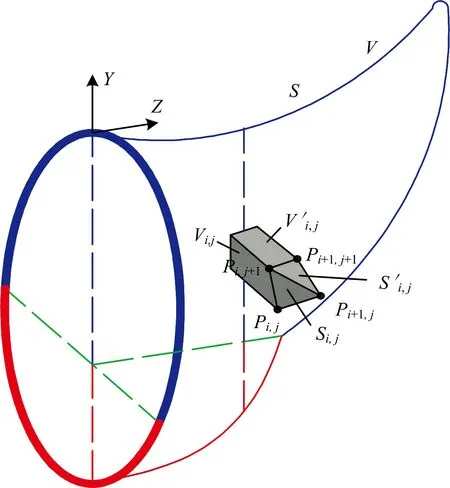
图9 单位体积和表面积滑块做功示意图
考虑到研究对象为刚性体,内力耗散功的唯一来源是土体沿着速度不连续面产生的塑性变形。内力耗散功功率沿速度间断面的单位功率是cδu,其中δu是沿速度间断面速度的正切。内力耗散功功率为沿不同单元面的单元内力耗散功功率之和,即
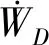
(41)
外力做功等于内力耗散功,即
(42)
将式(39)—式(41)代入式(42)并通过一定简化,可得开挖面失稳条件下的极限支护压力计算公式为
σc=γDNγ-cNc
(43)
其中,
(44)
(45)

4 单一地层各参数对极限支护压力的影响分析
为了验证本文所提方法的准确性,分别选取有、无黏聚力的单一地层,将本文提出的三维破坏机构对应的解分别与Mollon(2009)&(2010)提出的2种多块体模型和Leca&Dormieux(1990)提出的多块体模型对应的解进行比较。
假设隧道直径D=10 m,选取无黏聚力地层,土体容重γ=18 kN·m-3,黏聚力c=0,内摩擦角φ=20°,40°。采用本文提出的三维破坏机构和上述3种多块体模型分别求解无黏聚力地层不同覆跨比时的极限支护压力σc,计算结果如图10所示。

图10 无黏聚力地层覆跨比对极限支护压力的影响
由图10可知:针对无黏聚力地层,当覆跨比h/D≥1时,极限支护压力随覆跨比的增加保持为1个常数,这是由于开挖面前方土体的拱效应会阻止破坏面延伸至地表;在φ=20°,40°时,本文解与Mollon解(2010)相比分别提高了5.8%和10.5%;与Mollon解(2009)相比分别提高了13.5%和19.5%;与Leca&Dormieux解(1990)相比分别提高了30.4%和25.7%。
假设隧道直径D=10 m,土体容重γ=18 kN·m-3。定义2种黏性土:软黏土c=7 kPa,φ=17°,硬黏土c=10 kPa,φ=25°。采用本文提出的三维破坏机构和上述3种多块体模型分别求解极限支护压力σc,计算结果如图11所示。
由图11可知:h/D≥1时,极限支护压力σc保持不变;在软、硬黏土中,本文解与Mollon解(2010)相比分别提高了12.4%和34.9%;与Mollon解(2009)相比分别提高了36.5%和88.9%;与Leca&Dormieux解(1990)相比分别提高了62.3%和154.8%。

图11 黏性地层覆跨比对极限支护压力的影响
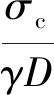

图12 地层黏聚力和内摩擦角对极限支护压力的影响
5 盾构开挖面极限支护压力计算结果与数值模拟结果对比验证
以国内地铁常用直径D=6 m的盾构隧道为例,不考虑地表超载,研究盾构隧道穿越2种地质强度差异较明显地层时的开挖面稳定性。定义盾构隧道穿越2种地质强度差异较大地层时,上部地层在开挖断面竖直方向上的厚度占开挖断面总高度的比例为η,即η=H/D。取η=1/6,1/3,1/2,2/3,5/6,研究η对开挖面稳定性的影响。同时研究2种地层的强度参数cu,φu和cd,φd对开挖面稳定性的影响。
考虑到盾构隧道开挖问题的对称性,为了提高数值模拟的计算速度,计算模型选取盾构隧道半对称模型。考虑盾构隧道开挖对周围地层的影响,要求计算模型的边界到隧道的距离不小于隧道开挖直径的3倍。三维模型边界范围:盾构直径为D,以隧道水平方向为X方向,取3.5D;以隧道掘进方向为Y方向,取9D;以隧道竖直方向为Z方向,隧道下部取D,上部覆土厚度h根据计算要求取2D。由此建立的考虑盾构隧道与土体相互作用的三维整体有限元模型如图13所示。

图13 三维整体有限元模型
计算采用的边界条件:模型上表面模拟地表,为无约束的自由边界,底部施加Z向竖直约束;模型关于YZ面对称,在模型的左右边界施加X向约束;在模型隧道开挖的前后边界施加Y向位移约束。
采用摩尔—库伦弹塑性模型模拟岩土体材料,采用结构单元壳单元模拟盾壳,采用各向同性弹性模型模拟管片及注浆体的应力—应变关系。
隧道埋深h=12 m,管片为C50钢筋混凝土材料,厚度0.3 m,注浆层为水泥砂浆,厚度0.14 m,盾体长9 m,盾壳厚度0.04 m。土体的物理力学参数、盾构盾壳、管片、注浆层的基本参数见表1。

表1 材料参数
5.1 内摩擦角差异对极限支护压力的影响
隧道穿越内摩擦角不同的2种砂性地层,上层砂土内摩擦角分别取φu=25°,30°,35°,下层砂土内摩擦角分别取φd=30°,35°,40°,理想的纯砂地层其黏聚力c=0,土体容重均取γ=20 kN·m-3,η=0.5。分别采用本文提出的理论计算方法和数值模拟方法进行求解,不同的φu,φd及η对σc影响的理论解与数值解对比如图14所示。
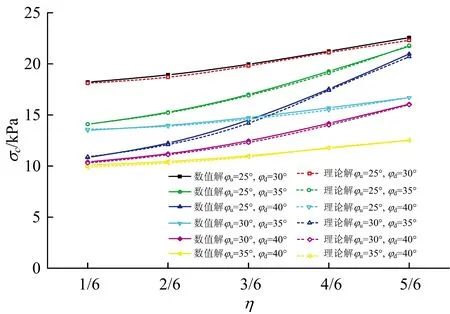
图14 不同的φu,φd及η对σc影响的理论解与数值解对比
由图14可知:不同的φu,φd及η条件下,极限支护压力的数值解与理论解在数值上有很好的吻合,差异在0.4%~1.45%之间,验证了本文提出的理论计算方法的准确性;隧道穿越下部地层内摩擦角φd不变,σc随上部地层内摩擦角φu的增大而减小,且上部地层在竖向占隧道断面比例越大,σc减小的趋势越明显;隧道穿越上部地层内摩擦角φu不变,σc随下部地层内摩擦角φd的增大而减小,且η越小,σc减小的趋势越大;σc随η的增大而增大,σc增大趋势随地层φu,φd差异及η的增大而增大。
5.2 黏聚力差异对极限支护压力的影响
隧道穿越黏聚力不同的2种黏性地层,上层黏土的黏聚力分别取cu=6,8,10 kPa,下层黏土的黏聚力分别取cd=8,10,12 kPa,假定2层土的内摩擦角均为φ=18°,土体重度均取γ=20 kN·m-3,η=0.5。分别采用本文提出的理论计算方法和数值模拟方法进行求解,不同的φu,φd及η对σc影响的理论解与数值解对比如图15所示。
由图15可知:不同的cu,cd及η条件下,极限支护压力的数值解与理论解在数值上有很好的吻合,差异在0.09%~8%之间,验证了本文提出的理论计算方法的准确性;而与图12结果对比发现,黏性地层中的理论解与数值解之间的离散性更大,对比Mollon[13]在单一地层中的研究成果显示,本文的理论解在无黏性地层中比黏性地层中更准确适用;隧道穿越下部地层黏聚力cd不变时,σc随上部地层黏聚力cu的增大而减小,且上部地层在竖向占隧道断面比例越大,σc减小的趋势越大;隧道穿越上部地层黏聚力cu不变,σc随下部地层黏聚力cd的增大而减小,且η越小,σc减小的趋势越大;σc随η的增大而增大,σc的增大趋势随地层cu,cd差异及η的增大而增大。

图15 不同的cu,cd及η对σc影响的理论解与数值解对比
对比图14和图15可知:内摩擦角、黏聚力差异对极限支护压力的影响,文中推导出的破坏机构主要受内摩擦角影响,而受黏聚力影响较小;文中推导出的极限支护压力受黏聚力影响较大。
6 结 论
(1) 通过极限分析上限法,对穿越分层地层盾构隧道开挖面稳定性计算方法进行了研究,建立了圆形盾构隧道穿越分层地层时开挖面失稳的三维破坏机构,推导了开挖面极限支护压力的计算方法。
(2) 利用本文得出的极限支护压力计算方法,分析了覆跨比h/D、地层黏聚力c、内摩擦角φ对单一地层开挖面极限支护压力的影响,并分别与前人提出的方法进行比较,验证了本文方法的准确性。
(3) 定义了η为盾构隧道穿越2种地质强度差异较大地层时,上部地层在开挖断面高度竖直方向上的厚度占开挖断面总高度的比例。仅考虑黏聚力及η差异时,极限支护压力σc随η的增大而增大,随着黏聚力差异增大而增大;仅考虑内摩擦角及η差异时,极限支护压力σc随η的增大而增大,随着内摩擦角差异增大而增大。并通过与数值模拟的极限支护压力对比,两者拟合度较高。
(4) 对比内摩擦角、黏聚力差异对极限支护压力的影响可知,本文推导出破坏机构的几何形态主要受内摩擦角影响,受黏聚力影响较小,本文推导出的极限支护压力受黏聚力影响较大。

