地铁DTⅥ2扣件弹条力学特性及断裂研究

陈宪麦，屈郑嘉，陈文韬，管吉波，李岳涛

(1.中南大学土木工程学院，湖南长沙，410075；2.中国铁路设计集团有限公司，天津，300142；3.深圳市地铁运营集团有限公司，广东深圳，518035)

目前，DTⅥ2 扣件已广泛应用于地下线短枕式整体道床，但在扣件实际服役过程中，弹条出现断裂破坏的情况十分常见。杜茂金[1]根据南京地铁DTⅥ2 型扣件弹条折断主要集中在小半径曲线地段的情况，从曲线地段轨道振动、弹条安装和设计缺陷、轨道不平顺等方面分析弹条断裂的原因，并提出相应整治措施。王鸿飞[2]对深圳地铁DTⅥ2 型扣件弹条断裂进行了研究，发现小半径曲线段钢轨波浪型磨耗会造成轨道振动剧烈从而导致弹条断裂；除此之外，扣件质量不合格和扣件安装流程不合理等也会造成弹条断裂。郭和平等[3]针对60Si2MnA 钢制弹条进行疲劳寿命试验，发现弹条表面质量差和表层存在脱碳层是导致弹条在未达到规定疲劳寿命时发生断裂的主要原因。尚红霞等[4]建立了III 型弹条扣件系统有限元模型，分析了不同安装状态和钢轨波磨下的弹条受力情况，发现钢轨波磨幅值越大，弹条应力幅值越大，加速了弹条疲劳破坏，建议弹条后端圆弧与铁垫板端部的距离应严格控制在8～10 mm，保证弹条的安装位置符合设计要求，以避免弹条出现应力集中的工作状态。目前，针对DTⅥ2 扣件弹条断裂问题的全面研究相对较少，为此，本文作者以DTⅥ2 扣件为研究对象，建立ABAQUS 有限元模型，从弹条本身的受力特性分析扣件服役过程中的不利影响因素，确定弹条的危险区域，开展DTⅥ2扣件弹条断裂的分析，以期为现场管控DTⅥ2扣件弹条失效提供技术支持。

1 扣件弹条失效

扣件弹条失效属于零部件失效，是从损伤或裂纹的产生到积累，直至零部件破坏的发展过程。王文秀等[5]的研究结果表明，扣件弹条在工作时承受复杂的弯曲扭转力作用，由此产生的应力集中在弹条表面。现场调研发现，常见DTⅥ2 扣件弹条失效模式如图1所示，图1(a)中，弹条断裂位置位于后拱小圆弧处[2]。图1(b)中，弹条断裂位置位于弹条跟端，断口呈明显的疲劳断裂特征。图1(c)中，I区为疲劳源区，是疲劳裂纹的萌生和疲劳裂纹扩展第1 阶段所在区域；II 区为疲劳裂纹扩展区，疲劳裂纹扩展区通常比较平整；III 区为疲劳瞬断区，当疲劳裂纹的扩展达到临界尺寸，裂纹截面无法承受外加载荷时，裂纹极速扩展，造成构件快速断裂，该区域呈放射条纹状，表面粗糙，这是截面应力超过材料承受极限造成的，这也是疲劳瞬断区的重要特征[6]。

图1 DTⅥ2扣件弹条断裂模式Fig.1 Fracture modes of DTⅥ2 fastener elastic bar

2 有限元模型

DTⅥ2 扣件为弹性分开式扣件，适用于城市轨道交通工程地下线、地面线和高架线60 kg/m钢轨整体道床地段[7]，弹条形状为“e”型弹条，直径为18 mm。

本文重点分析弹条在预加载及荷载作用下产生的应力以及扣压力等力学参数，简化螺栓道钉、尼龙套管等对受力分析影响较小的部件，并以边界条件取代其提供的定位、减振作用。模型分为弹条、铁垫板和绝缘轨距块3个部分，采用六面体单元网格。本文所建的DTⅥ2 扣件有限元模型如图2所示。

图2 DTⅥ2扣件有限元模型Fig.2 Finite element model of DTⅥ2 fastener

弹条的材料为60Si2Mn 弹簧钢，屈服强度为1 200 MPa，抗拉强度为1 300 MPa[8]，铁垫板的材料为球墨铸铁。绝缘轨距块的主要作用是绝缘和调整轨距，设置为刚体。模型所取材料参数见表1。

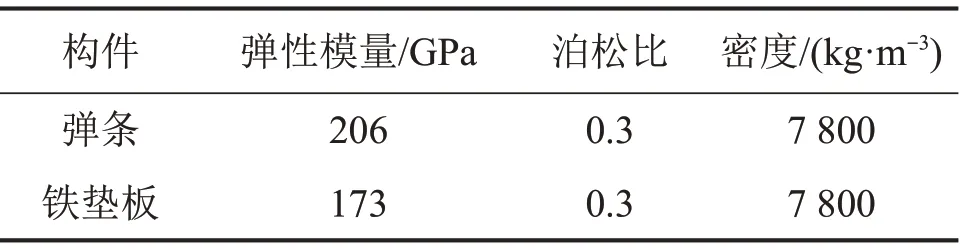
表1 材料参数Table 1 Material parameters

弹条随着弹程变化而改变接触状态的问题属于非线性接触问题[9−10]，在扣件系统正常安装状态下，弹条趾端下表面与绝缘块上表面、弹条中肢上表面和铁垫板圆孔上表面、弹条跟端下表面与铁垫板跟端座上表面存在接触，如图3所示。采用非线性有限元接触理论[11]进行分析，3个接触面均设置为罚函数摩擦公式，摩擦因数取0.3，法向行为选择“硬”接触。模型中不设置承轨台，对铁垫板底部设置全约束。在实际情况中，钢轨可能产生位移变化，因此，需约束绝缘轨距块除竖向自由度外的其他5个自由度[4]。

图3 扣件系统接触部位Fig.3 Contact regions of fastener system

2.1 扣压力验证

扣件必须有足够的扣压力以保证钢轨与支撑体之间的联结，DTⅥ2 扣件初始扣压力为8 kN，弹程为10.5 mm[12]，模型验证时取扣件正常安装时弹条内侧圆弧与铁垫板支座之间的距离为9 mm。当弹条变形达到初始弹程时，由模型计算得到弹条扣压力为8.65 kN，超过扣件设计初始扣压力(8 kN)，满足扣压力要求。

2.2 应力验证

采用第四强度理论作为评价指标，弹条Mises等效应力如图4所示。从图4可以看出：在正常安装状态下，小圆弧内侧区域处应力较大，同时，弹条跟端底部部分区域也有应力较大的单元出现，最大等效应力为1 188 MPa，小于材料屈服强度(1 200 MPa)。

图4 正常安装状态下弹条最大等效应力分布Fig.4 The maximum equivalent stress distribution of elastic bar under normal installation state

3 扣件弹条力学特性分析

模拟现场弹条的安装状态对弹条受力的影响，以弹条等效应力和扣压力为主要评价指标，探究不同工况对弹条受力情况的影响。

3.1 弹条安装状态对扣件系统受力的影响

3.1.1 弹条内侧圆弧与铁垫板的距离对扣件系统受力影响

分析弹条小圆弧内侧与铁垫板的距离对弹条受力的影响，取弹条弹程为正常安装值10.5 mm，计算工况见表2，计算结果分别如图5～7所示。

表2 不同工况下弹条小圆弧内侧与铁垫板的距离(d)Table 2 Distances between inner side of small arc of elastic bar and iron plate at different working conditions

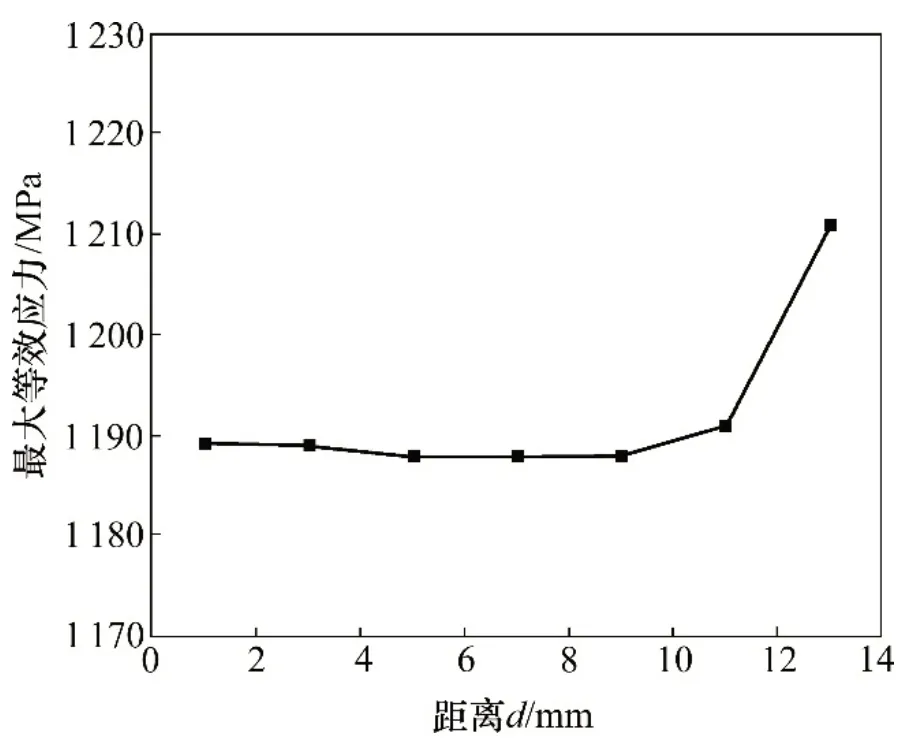
图5 最大等效应力与距离(d)的关系Fig.5 Relationship between the maximum equivalent stress and distance(d)

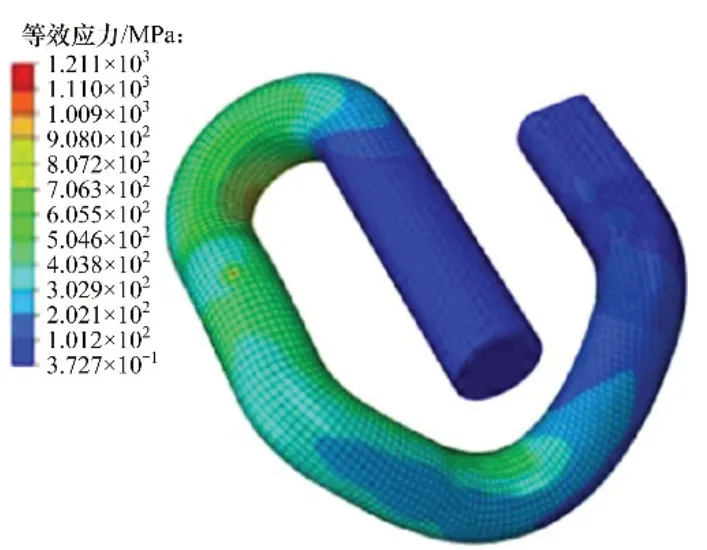
图6 弹条最大等效应力分布(d=13 mm)Fig.6 The maximum equivalent stress distribution of elastic bar(d=13 mm)

图7 扣压力与距离(d)的关系Fig.7 Relationship between clamping force and distance(d)

由图5可知：当弹条小圆弧内侧与铁垫板的距离从1 mm增加至11 mm时，弹条产生的最大等效应力基本保持在1 190 MPa 附近；当距离达到13 mm 时，弹条的最大等效应力达到1 211 MPa，超过材料屈服应力1 200 MPa，产生塑性变形。由图6可知：等效应力最大区域为弹条小圆弧内侧和跟端下侧与铁垫板接触部分。

由图7可知：当弹条弹程满足要求时，弹条扣压力为8.64～8.65 kN，满足弹条运营需求，弹条小圆弧内侧与铁垫板的距离对扣压力影响不大。因此，只要弹条内侧没有完全与铁垫板接触，则不会造成弹条处内部初始应力集中而导致弹条强度降低的情况。

3.1.2 弹程对扣件系统受力影响

在扣件弹条实际的安装过程中，安装情况与设计的初始弹程往往有误差，因此，需要分析在非正常安装条件下弹条的受力情况，不同工况下的弹条弹程L如表3所示，计算结果分别如图8～10所示。

表3 不同工况下弹条弹程(L)Table 3 Vertical displacements(L)of elastic bar at different working conditions

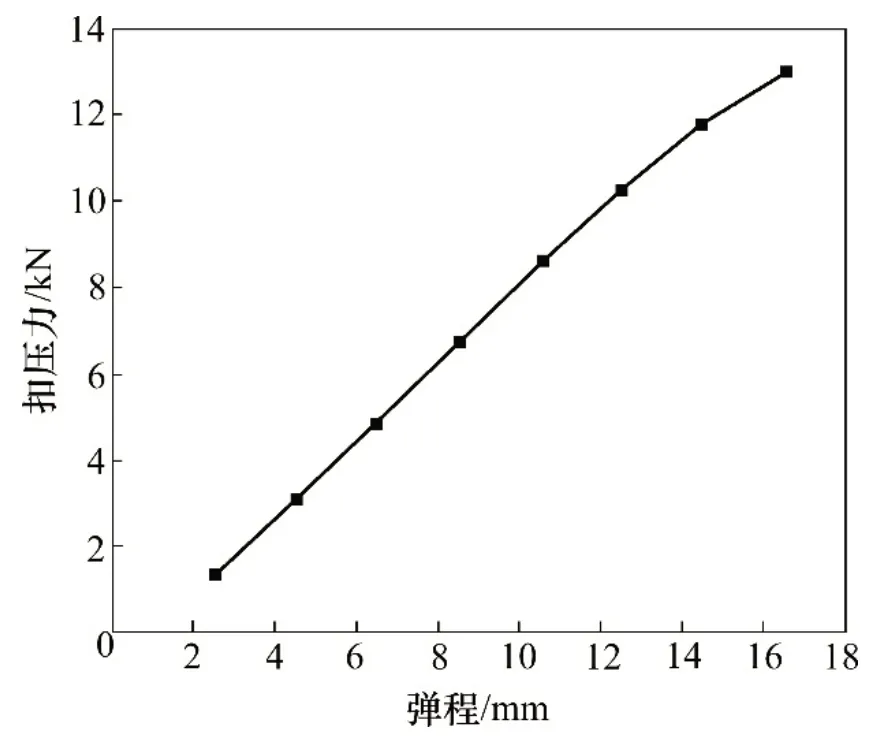
图8 扣压力与弹程的关系Fig.8 Relationship between clamping force and vertical displacement

由图8可知：随着初始弹程增大，DTⅥ2弹条弹程与扣压力的关系曲线由线性转变为非线性。DTⅥ2 型弹条扣件的扣压力与其弹程的关系总体上为线性关系，表明扣件在一定的变形情况下，扣件弹程与扣压力成正比，扣压件产生弹性变形，其斜率为扣件弹条的弹性系数；当弹条变形达到初始弹程时，弹条扣压力为8.65 kN，扣件处于正常安装状态；当弹条趾端变形大于12 mm 时，扣压力与弹程的关系曲线出现非线性变化。

图9 最大等效应力与弹程的关系Fig.9 Relationship between the maximum equivalent stress and vertical displacement

图10 不同弹程下弹条最大等效应力分布Fig.10 The maximum equivalent stress distribution of elastic bar with different vertical displacements

结合图9和图10 可知：弹条小圆弧内侧及弹条跟端与铁垫板接触部分应力超过屈服强度发生塑性变形[13]，随着弹程增大，塑性区扩展从弹条小圆弧内侧及跟端接触部分扩展至小圆弧外侧及整个弹条跟端区域，产生较大的塑性形变。与弹性区域不同的是，发生塑性变形的区域在卸载后仍会产生一定的塑性变形。在列车荷载的循环作用下，此处易萌生裂纹并发展，最终导致弹条断裂扣件失效。这一现象与弹条现场断裂现象(见图1)一致，因此，DTⅥ2 型扣件弹条正常工作弹程为10.5～12 mm，此时扣压力满足要求。

3.2 摩擦因数对扣件弹条受力的影响

弹条与铁垫板的接触位置和接触面积是逐渐变化的，因此，需要探究两者接触部分的摩擦因数对扣件弹条受力的影响。其中，弹条与铁垫板存在2个接触部分，即弹条中肢上表面和铁垫板圆孔上表面、弹条跟端下表面与铁垫板跟上表面。初始弹程取10.5 mm，弹条小圆弧内侧与铁垫板支座的距离取9.0 mm，不同工况下摩擦因数μ见表4，计算结果如图11～13所示。

表4 不同工况下摩擦因数(μ)Table 4 Frictional coefficient(μ)at different working conditions

图11 最大等效应力与摩擦因数的关系Fig.11 Relationship between the maximum equivalent stress and friction coefficient

由图11和12 可知：随着摩擦因数增大，弹条各区域等效应力基本一致，最大等效应力及出现区域差别不大，弹条出现塑性的区域依然是小圆弧内侧及跟端与铁垫板接触部分，可见摩擦因数的变化对弹条等效应力影响不大。

由图13 可知：随着摩擦因数增大，扣压力略有增大，且当摩擦因数小于0.2时，扣压力增加幅度较大；当摩擦因数大于0.2时，扣压力变化幅度减小；不同摩擦因数下扣压力均大于8 kN，满足要求。

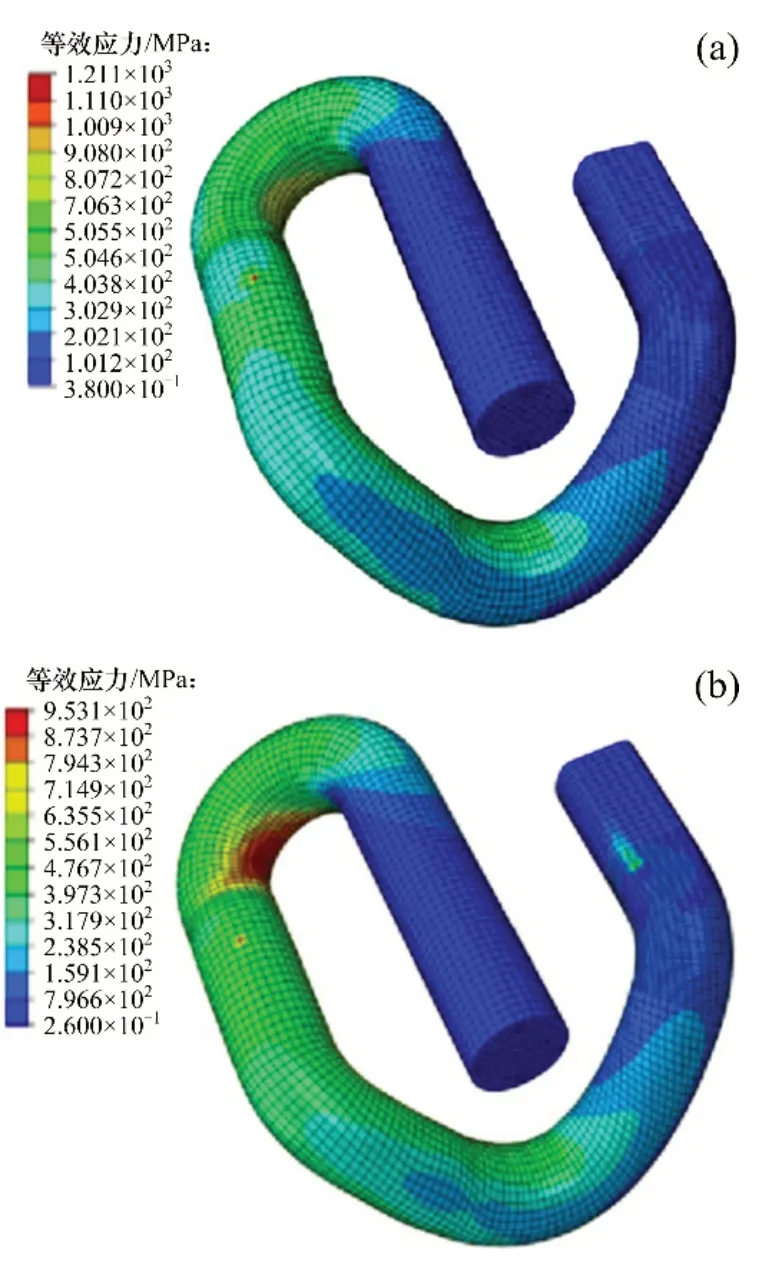
图12 不同摩擦因数下弹条最大等效应力分布Fig.12 The maximum equivalent stress distribution of elastic bar with different friction coefficients

图13 扣压力与摩擦因数的关系Fig.13 Relationship between clamping force and friction coefficient

3.3 地铁环境温度对DTⅥ2扣件弹条力学性能的影响

经研究发现，东京地铁内的温度由1945年的25 ℃上升至1989年的33 ℃(8月份)。在纽约地铁也同样出现了地铁开通后热环境恶化的现象。根据资料统计，我国北京地铁内的温度以每年0.2～0.3 ℃的速度增长，至1995年夏季，其最高温度已经达到31 ℃，远远地超过了设计时的25 ℃[14]。另外，我国青海、西藏和东北等地最低气温达到−40 ℃以下，因此，研究温度对扣件弹条力学性能的影响具有重要的工程应用价值。不同工况对应的环境温度如表5所示。取室温25 ℃，60Si2Mn弹簧钢传热系数取40 W∙(m∙K−1)[15]，计算结果分别如图14～16所示。

表5 不同工况对应的环境温度(t)Table 5 Temperature(t)corresponding to different working conditions

图14 扣压力与温度的关系Fig.14 Relationship between clamping force and temperature

由图14 可知：当弹条弹程满足要求时，在温度从30 ℃下降至−20 ℃的过程中，DTⅥ2 型扣压力略有下降，从8.66 kN降低至8.62 kN；不同温度下扣压力均大于8.0 kN，基本满足扣件使用要求。

由图15 可见：随着温度由−20 ℃上升到30 ℃，弹条最大等效应力总体呈现下降趋势；当温度为−20 ℃时，弹条最大等效应力为1 207 MPa。由图16 可以看出：−20 ℃时塑性区域依然是小圆弧内侧及跟端与铁垫板接触部分。总体而言，温度变化对弹条最大等效应力影响不大。

图15 弹条最大等效应力与温度的关系Fig.15 Relationship between the maximum equivalent stress of elastic bar and temperature

图16 弹条最大等效应力分布(t=−20 ℃)Fig.16 The maximum equivalent stress distribution of elastic bar(t=−20 ℃)

4 瞬态动力响应分析

现场调查发现钢轨出现较明显波磨，根据已有研究可知，钢轨波磨的存在是导致DTⅥ2 型扣件弹条折断的主要原因，钢轨波磨使得轨道振动加剧[1]。

根据地铁现场波磨调查结果，线路上的主波长为20～25 mm，车辆实际运行速度为68 km/h。频率f计算公式为

式中：v为波速；λ为波长。由式(1)计算得到波磨实际通过频率为755～944 Hz，即该区段波磨病害能够激发起轨道755～944 Hz的振动响应。

4.1 弹条模态分析

对自由状态下弹条三维实体有限元模型进行模态分析，根据现场调研和钢轨波磨对弹条断裂影响[16]所涉及的通过频率，对2.0 kHz 以内的固有模态进行分析[17]。弹条各部分示意图如图17所示，弹条模型的低阶振型如图18所示(实体单元为弹条发生振动时的变形情况，虚化单元为弹条发生振动变形前的位置)。

图17 弹条各部分示意图Fig.17 Diagram of each part of elastic bar

弹条前4 阶固有频率及模态振型描述见表6。其中，第1和第3阶振动使得弹条中肢及圆弧处产生剪力和拉力作用，促进弹条中肢根部受扭转剪力和拉压力发生疲劳损伤。结合现场调查，发现20～25 mm 波长的波磨在车速为68 km/h 时激发的振动频率与弹条第1和第2阶固有频率相近，容易引发共振现象导致弹条断裂。

4.2 谐响应分析

图18 弹条各阶振型Fig.18 Vibration modes of elastic bar

表6 弹条前4阶固有频率及振型描述Table 6 Natural frequency and description of the first four vibration modes of elastic bar

弹条在列车动荷载作用下，由于轨道不平顺的激励作用，在特定条件下会达到某个频率的共振，使得部件在该频率振动情况下以更大的振幅振动，加速扣件弹条的破坏。而弹条在正弦激振力作用下的谐响应应力和谐响加速度能够反映出弹条的敏感频带。结合模态振型，对弹条进行谐响应分析，将作用于弹条趾端的动态力简化成作用于趾端下表面中心的单位正弦力，结合现场调查扫频分析频率范围取0～2.0 kHz，在自由状态下，弹条各部位的最大等效应力和垂向加速度分别如图19和图20所示。

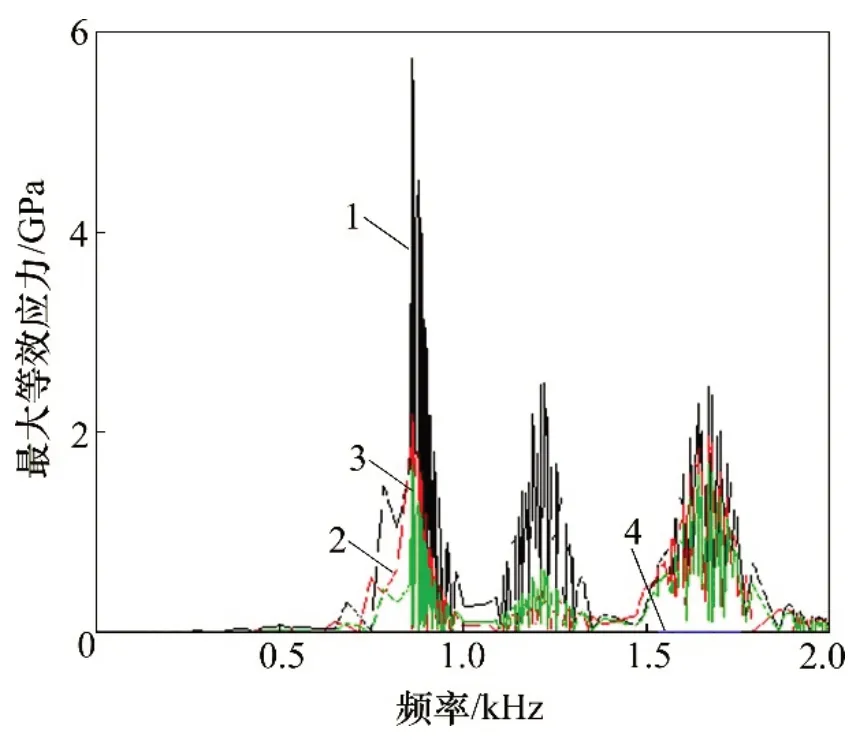
图19 弹条不同部位谐响应应力Fig.19 Harmonic response stress of elastic bar at different positions

图20 弹条不同部位谐响应加速度Fig.20 Harmonic response acceleration of elastic bar at different positions

由图19 可知：首先出现较大弹条谐响应应力的振动波段782～934 Hz 为钢轨波磨的通过频率，与弹条自由状态下的第1和第2阶模态的固有频率相近，表明DTⅥ2 型扣件弹条的固有频率与典型钢轨波磨的通过频率接近，因此，在典型钢轨波磨的激励下，弹条易产生共振，从而增大弹条的振动幅值，加速弹条的疲劳损坏，造成弹条突然断裂。其中，弹条小圆弧内侧和跟端最大等效应力明显大于大圆弧拱顶和趾端最大等效应力，并且已经远远超过弹条的屈服强度，使弹条产生塑性变形，且该处是弹条断裂常发生的位置。运用第四强度理论Mises应力进行表征，弹条谐响应应力如图19所示。当受到该频率的激振作用引起共振时，容易造成弹条的小圆弧内侧应力较大，从而引起断裂，与现场弹条断裂位置吻合(见图1)。除了上述频率外，在频率1 160～1 270 Hz和1 620～1 700 Hz范围还存在峰值，分别与弹条自由状态下第3和第4阶固有频率相近。因此，列车通过钢轨波磨地段时，除了引起钢轨波磨通过频率处的弹条强迫振动外，还会引起这些频率附近弹条固有频率处的振动。

由图20 可知：在单位正弦激励作用下，弹条各部分振动加速度明显且存在差异，弹条各部位的垂向加速度出现了3个较明显的峰值，对应频率分别为782～934，1 160～1 270和1 620～1 700 Hz，弹条小圆弧内侧和跟端部分振动加速度振幅较大，最大振幅约为180g，趾端部分和大圆弧拱顶部分振幅较小，但也出现在相应频率范围内加速度增大的现象，说明在0～2.0 kHz 激扰源激励作用下，这些区域容易因突变振动而产生破坏。

5 结论

1)当弹条弹程一定时，随着弹条小圆弧内侧与铁垫板支座距离减小，弹条的最大等效应力基本保持不变，最大等效应力产生区域为弹条小圆弧内侧及跟端下侧与铁垫板接触部分；当弹条内侧圆弧与铁垫板支座的距离一定时，随着弹条弹程的增加，弹条大圆弧、小圆弧和跟端的最大等效应力逐渐增大，且小圆弧内侧及跟端靠近铁垫板部分应力最大，当弹程大于12 mm 时，弹条小圆弧内侧及弹条跟端与铁垫板接触部分应力超过屈服极限发生塑性变形，在列车荷载的作用下，此处容易萌生裂纹并发展，最终导致弹条断裂扣件失效；摩擦因数变化对弹条力学性能影响较小。

2)在环境温度上升过程中，DTⅥ2 扣件扣压力略有增加，满足扣件使用要求；最大等效应力略有减小，出现塑性的区域依然是小圆弧内侧及跟端与铁垫板接触部分，温度变化对弹条力学性能影响较小。

3)当频率分别为782～934，1 160～1 270和1 620～1 700 Hz时，弹条各部位的最大等效应力和垂向加速度出现了3个较明显的峰值，与现场波磨激发的钢轨振动频率相近，引发共振现象，促使弹条断裂。