考虑中间主应力的粉砂岩侧向卸荷力学特性试验研究

马钰沛，李江腾，刘双飞

(中南大学资源与安全工程学院，湖南长沙，410083)

岩体一般处于三向应力状态，边坡、基坑、隧道的开挖卸荷使岩体某一方向的应力得到释放，开挖面附近的岩体应力重新分布。同时，高地应力区的开挖卸荷容易造成岩石在卸荷方向强烈扩容，其破裂主要有张性破裂，并伴随着剪切破坏发生[1]，岩体承载能力降低，变形增大，影响着边坡的稳定性，因此，研究卸荷条件下岩石变形破坏机制对工程开挖很有意义。近年来，研究者对大理岩、花岗岩、砂岩在卸荷状态下岩体的破坏特征进行了大量的试验与力学研究[2−9]，但这些研究都是在常规三轴力学试验(σ1>σ2=σ3，σ1，σ2和σ3分别为最大、中间和最小主应力)条件下进行的，而实际开挖工程中应力多呈非等围压状态，而且中间主应力对岩石的强度、变形和体积膨胀等性质有重要影响[10−12]，忽略中间主应力σ2的影响无法真实反映边坡开挖中卸荷所引起的岩体破坏。为此，李建林等[13]将高边坡岩体卸荷试验结果与三维数值模拟结果相比较，对高陡边坡在卸荷应力状态下的岩体应力应变关系进行研究，以分析岩体各阶段的宏观力学参数。王蒙等[14]通过真三轴加卸载破坏试验研究了不同倾角裂隙岩体的变形破坏特征和应力脆性跌落系数变化规律。陈国庆等[15]开展了不同中间主应力真三轴卸荷试验，研究了岩质边坡开挖卸荷的破坏模式，为节理岩质边坡开挖卸荷稳定性识别提供了科学依据。傅鹤林等[16]结合真三轴试验结果研究了不同强度本构模型随中间主应力系数b变化的计算公式。目前，对于考虑中间主应力条件下的岩石真三轴卸载力学特性还有待于进一步研究。本文作者以粉砂岩为研究对象，参考实际边坡开挖应力变化，通过试样在不同应力状态、不同中间主应力系数b条件下的真三轴侧向卸荷破坏试验，研究试样岩体在卸荷条件下的破坏、变形特征，以Mogi-Coulomb强度准则为基础，讨论中间主应力对卸荷岩石强度的作用。

1 试验方案

1.1 试验条件

图1 TRW-3000岩石力学试验机Fig.1 Rock mechanics testing machine of TRW-3000

试验使用TRW-3000 型岩石真三轴力学试验机，试验设备如图1所示。该试验系统能够模拟三向独立的加卸载应力对岩石试样的影响。试验试样长×宽×高为100 mm×100 mm×100 mm。取自均质性良好的完整粉砂岩块，不平行度和不垂直度均小于0.5 mm。

1.2 试验方案

取相邻采样部位2个试样为1组，采用不同的中间主应力系数b(0，0.4，0.8和1.0)对试件进行不同围压下的加载和卸载试验，应力路径如图2所示，其中，b=(σ2-σ3)/(σ1-σ3)。三轴压缩试验参照文献[17]，试验方案具体如下。

图2 应力路径示意图Fig.2 Sketch diagrams of stress paths

方案Ⅰ：真三轴加载试验。该试验为卸载试验提供压缩强度、破坏特征。设计不同应力水平的压缩试验，其最小主应力分别为2，6和10 MPa。以0.2 MPa/s的速率施加最大主应力σ1直至试样破坏。

方案Ⅱ：真三轴卸载试验。基于高陡边坡开挖前后的应力调整及卸荷方式，试验初始应力条件见表1。试验步骤为：1)按静水压力条件(速率为0.2 MPa/s)施加σ1，σ2和σ3至预定值，稳定30 s；2)保持σ2和σ3恒定，施加σ1至试样破坏前某一应力(取相应应力条件下真三轴压缩试验所得岩石三轴抗压强度的90%)，保持σ1恒定；3)以速率0.05 MPa/s卸载σ3直至试样破坏。

表1 真三轴加卸载试验初始应力条件Table 1 Initial stress conditions of true triaxial loading and unloading tests

2 破坏特征分析

岩石的破坏伴随着微裂纹压密、裂隙的产生、扩展贯通的过程，最终形成岩石局部剥离。破坏面的形成受岩石自身的物理性质和受力状态的影响，常规三轴压缩试验试样主要宏观破坏模式为剪切破坏(低围压)和塑性破坏(高围压)。在真三轴试验中，岩石的破坏模式随应力变化表现出差异性。

2.1 破坏面倾角分析

在真三轴应力条件(σ1>σ2>σ3)下，σ3方向卸荷后，岩石试样出现走向平行于σ2，倾向与σ3存在一定夹角(如图3所示θ)的破坏面。

根据试验结果，在侧向卸荷作用下，破坏面倾角θ随中间主应力增大近似呈线性增大，如图3所示。其中，R2为决定系数。当中间主应力系数b从0 增加到1 时，3 组应力破断角分别增加22.6%，26.4%和22.2%。其原因是随着中间主应力系数b增大，σ3逐渐减小，在沿着卸荷面方向，更容易形成裂纹并发生扩展。

图3 b不同时的破断角Fig.3 Fracture dip angles under different b

2.2 破坏模式分析

不同中间主应力侧向卸荷粉砂岩破断面形态如图4所示(以编号SO-2组为例)。从图4可见：沿着卸荷方向产生明显侧向膨胀，卸荷面有部分张性碎落片。试样破坏时发出清脆响声，表现为脆性破坏特征。

当中间主应力系数b为0和0.4 时，试验砂岩破坏表现为剪切破坏，破坏面出现大量细小岩粉及碎裂岩块，有明显的剪切摩擦的痕迹，且沿着卸荷面有裂纹扩展；当中间主应力系数b＝0.8时，试验砂岩沿着卸荷方向发生板裂破坏，局部出现剪切破坏；当中间主应力系数b＝1 时，岩石内部形成与卸荷方向垂直的粗糙破裂面，随着偏应力增大，破裂岩块屈服变形并发生板裂破坏，板裂现象表现为片状和薄板状。

由此可见：随着中间主应力增大，试验粉砂岩卸荷破坏模式由剪切−张拉复合破坏转变为板裂张拉破坏；同时，岩体卸荷破坏时所受偏应力比加载破坏时的大，所以，在相同的初始应力条件下，卸荷试样破坏更加剧烈。

3 变形特性

3.1 应力−应变关系

图5所示为不同中主应力系数条件下的应力−应变曲线(以编号SO-2 组为例)，由于试样破坏时使用应力控制，故只得到峰前应力−应变关系曲线。从图5可以看出：

1)与常规三轴压缩试验类似，真三轴加卸载试验应力−应变曲线也大致经历了岩石微裂隙压密—弹性变形裂纹扩展贯通—破坏阶段。试样屈服前有一定的塑性变形，但其破坏仍是脆性破坏。

2)粉砂岩在不同中间主应力系数下的侧向卸荷应力−应变曲线变化近似。最大主应变ε1和最小主应变ε3随b不断增大而增大，中间主应变ε2曲线的斜率越来越大。其原因是随着σ2增大，σ3方向卸荷，σ2方向的变形得到的约束由扩张(b＜0.5)逐渐变为压缩(b≥0.5)[18]，由泊松效应引起的侧向膨胀沿着卸荷面方向增大，较小的约束力增大了平行于卸荷面的裂纹扩展和沿着σ3方向的张性破坏。粉砂岩试样破坏时的应变如表2所示。

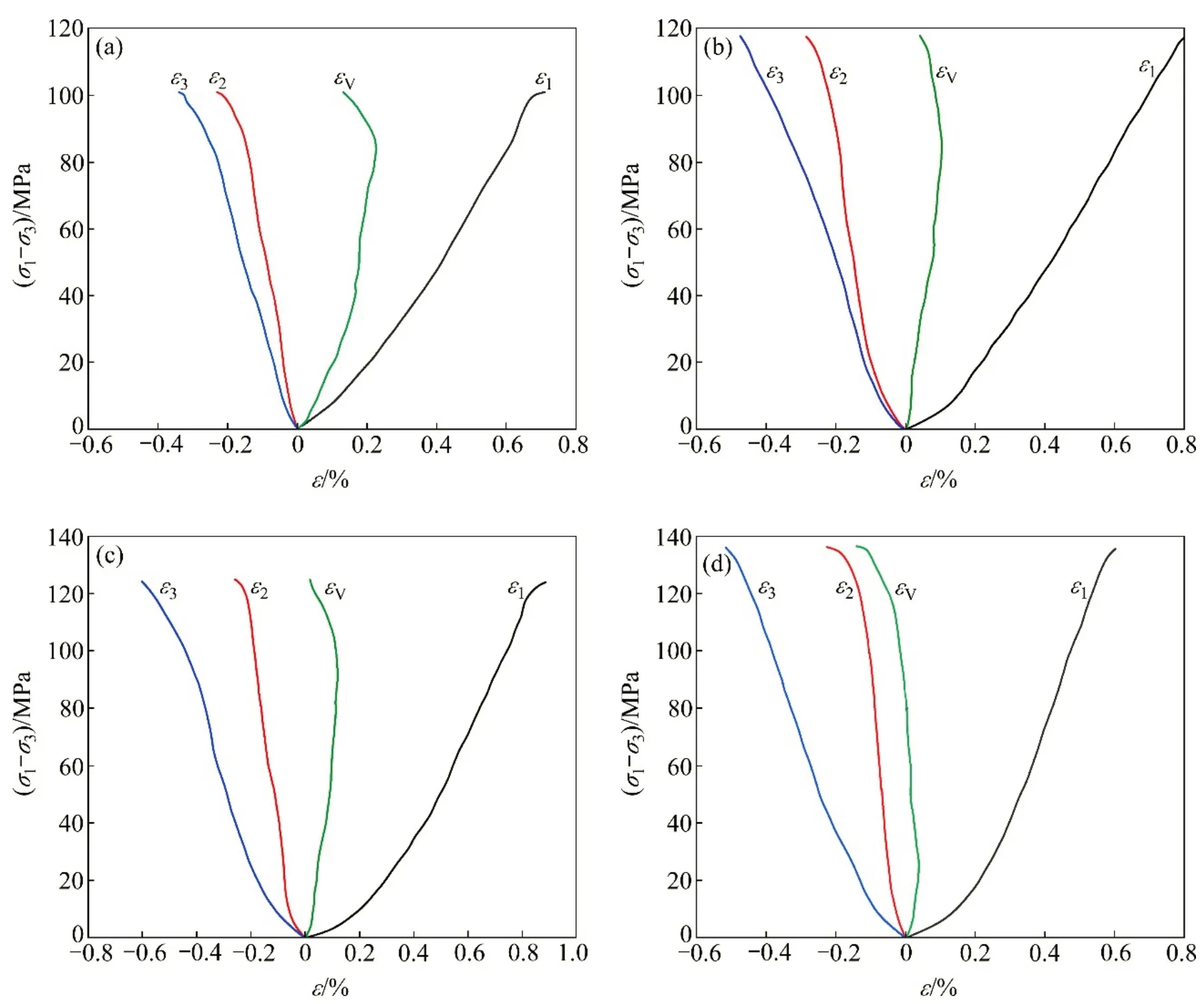
图5 不同中间主应力系数下卸荷试验应力−应变曲线Fig.5 Stress−strain curves of unloading tests in different intermediate principal stress coefficients

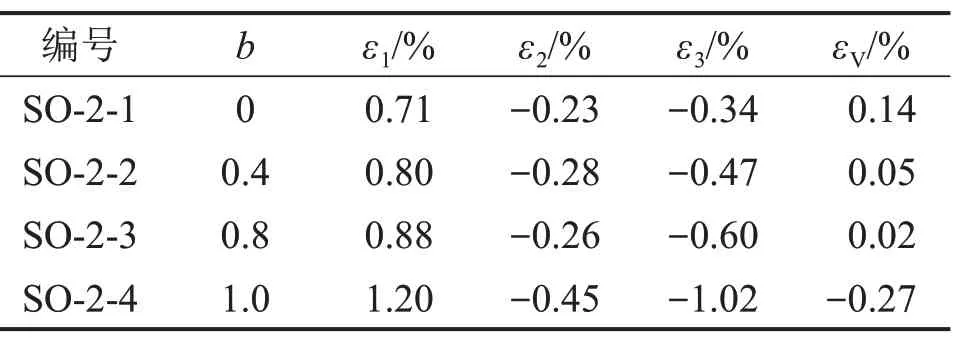
表2 真三轴侧向卸荷试验岩样破坏应变Table 2 Failure strain of rock specimens of true triaxial lateral unloading tests

3)体积应变曲线出现较明显的分段现象。当加载到一定阶段时，曲线负向弯曲，体积应变偏离线性段转变为非线性段，即发生体积回转现象；应变曲线偏离线性段的转折点随着b增大逐渐降低；试样体积应变εV随着b增大而减小，呈现扩容趋势。

3.2 变形模量

根据试验应力路径，加卸载过程中仅σ1和σ3中的1个主应力发生变化，故dσ1=0 或dσ3=0，且dσ2=0，增量型广义虎克定理可简化为

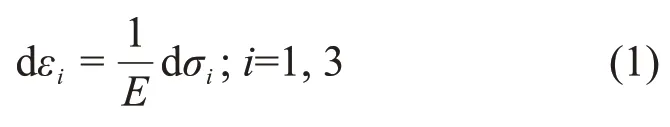
式中：dεi和dσi分别为应变和应力增量；E为卸荷过程中的变形模量。变形模量与卸荷量有关，使用对数函数拟合卸荷变形曲线(见图6)：

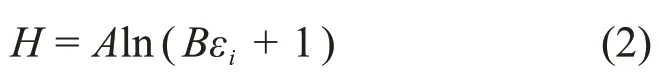
其中：

式中：A和B为拟合参数；H为卸荷量，表征应力卸荷程度；σ0为卸荷初始应力，为6 MPa。由式(1)和(2)得卸荷过程中变形模量E与H的计算公式(关系曲线见图7)：

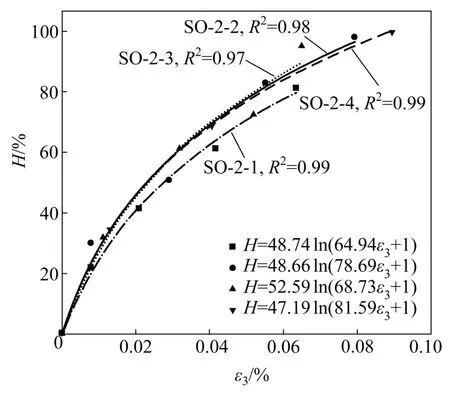
图6 ε3与H拟合曲线Fig.6 ε3−H fitting curves

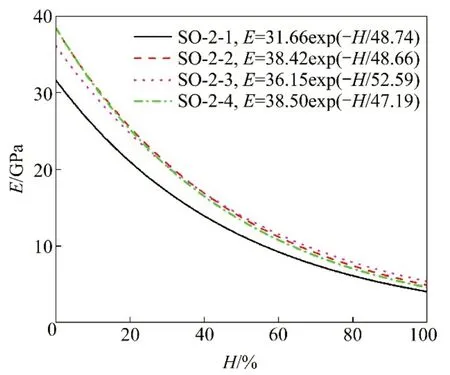
图7 E与H关系曲线Fig.7 Relationship between E and H

由图7可知：在卸荷过程中，粉砂岩变形模量呈指数下降；初始围压越大，卸荷变形更加剧烈，较小的卸荷应力能导致岩样发生剧烈破坏。

4 强度分析

4.1 真三轴卸荷强度特性

岩石强度在常规三轴应力条件下随围压增大近似呈线性增大，但在真三轴应力条件下表现更加复杂。粉砂岩破坏峰值强度随中间主应力的变化情况如图8所示。由图8可知：随着中间主应力系数增大，试样破坏时的最大主应力也逐步增大，可用二次多项式表示，其拟合结果较线性拟合结果更准确。

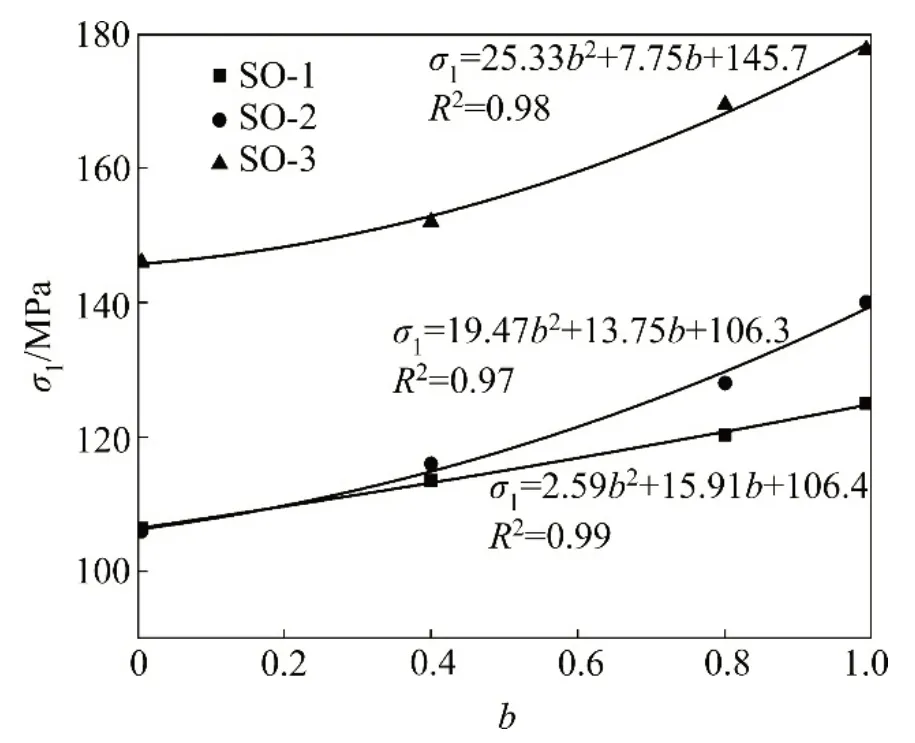
图8 中间主应力系数b与最大主应力σ1关系曲线Fig.8 Relationships between intermediate principal stress coefficient and the maximum principal stress

真三轴条件下中间主应力σ2对卸荷破坏峰值强度有较大影响。3 组试验中，当中间主应力b从0增大至1 时，粉砂岩卸荷破坏时的峰值分别升高17.5%，32.0%和21.6%，所以，粉砂岩侧向卸荷破坏峰值强度随中间主应力增加有所增大。

4.2 考虑中间主应力的岩体强度

MOGI[19]通过大量真三轴试验，主要考虑岩体破坏时的八面体剪应力τoct和有效中间主应力σm,2，提出强度准则：

AI-AJMI 等[20−22]将MOGI经验强度准则与Coulomb强度准则相结合，发现采用f(σm,2)的线性函数拟合较理想，并将之称为Mogi-Coulomb(简称Mogi-C)强度准则：

式中：c为黏聚力，MPa；φ为内摩擦角；p为Mogi-Coulomb 准则拟合直线与τoct轴的截距；q为拟合直线斜率。结合式(6)和(7)，由有效应力张量第一不变量I1、第二不变量I2推得Mogi-Coulomb准则的另外一种形式：

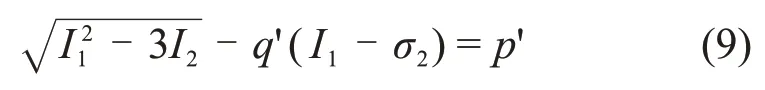
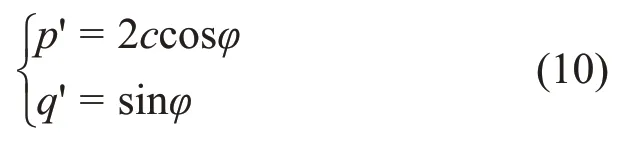
考虑中间主应力效应的Mogi-Coulomb强度准则拟合曲线见图9，由图9 得强度准则系数，结合式(8)可以分别得到Mogi-Coulomb 强度准则的c和φ及八面体剪应力强度平均偏差τ，如表3所示。τ计算公式为

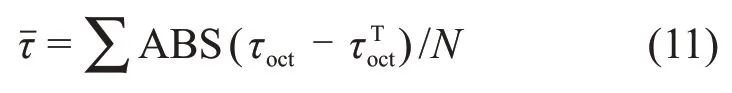
式中：ABS为绝对值函数，τoct和分别为强度计算值和试验值，MPa；N为试验次数。

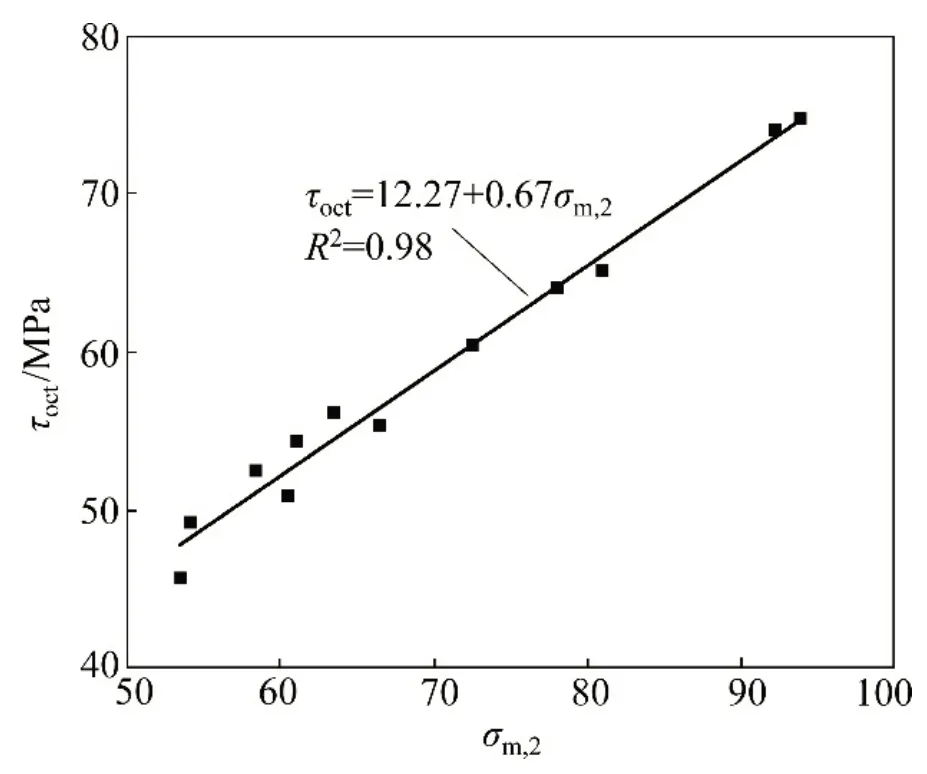
图9 真三轴侧向卸载破坏τoct-σm,2关系曲线Fig.9 τoct-σm,2 relationship of true triaxial lateral unloading tests

表3 真三轴侧向卸荷Mogi-Coulomb强度准则拟合结果Table 3 Mogi-Coulomb strength criteria’s fitting results of true triaxial lateral unloading tests

通过试验获得粉砂岩的黏聚力c、内摩擦角φ，代入式(10)得p′=26.03，q′=0.71。将试验值代入式(9)，得到p′平均值为25.40，与式(10)计算参数p′比较平均相对误差为2.4%。

由图9和表3 可以看出，试验结果与Mogi-Coulomb 强度准则的拟合结果吻合度较高。Mogi拟合的均值为0.98，拟合度较高，而且强度平均偏差τ较小。

对于拟合回归系数能否准确表示砂岩真三轴卸荷破坏强度，仍需要对Mogi-Colomb 强度准则的拟合方程进行显著性检验。根据拟合方程与式(5)，使用试验值σ2和σ3计算得到σ1和τoct的反算值，采用F检验法，得到反算值偏差分析结果如表4所示。

通过查F分布表求出临界值Fα(1,n-2)：

将表4中的F统计量与查F分布表中获得的不同显著性水平的临界值Fα(1,n-2)进行比较可见：3 组试验均有F>F0.01(1,2)，说明Mogi-Coulomb强度准则的拟合回归方程高度显著于α=0.01的检验要求，即拟合方程与实际试验重合概率为99%。所以，采用Mogi-Coulomb强度准则可以较好地反映试验砂岩在真三轴侧向卸荷应力条件下的强度特征。

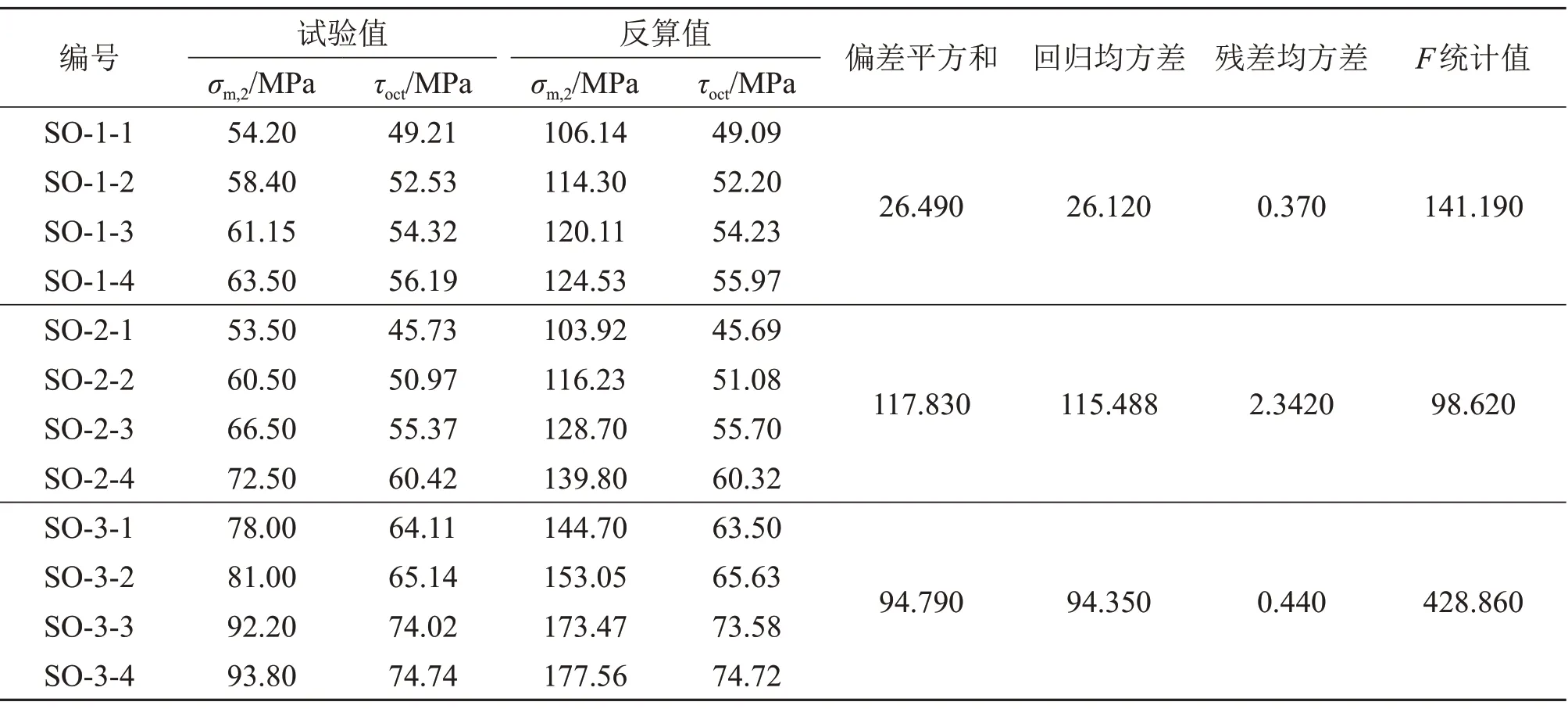
表4 粉砂岩强度Mogi-Coulomb准则反算值及方差分析Table 4 Back-calculated values of siltstone based on Mogi-Coulomb criterion and analysis of variance

5 结论

1)在真三轴应力条件下，粉砂岩破断面倾角θ随中间主应力增大近似呈线性增大，破坏模式由剪切−张拉复合破坏转变为板裂破坏。

2)真三轴侧向卸荷应力−应变曲线中试样破坏前发生塑性变形，但最终表现出脆性破坏特征。随着中间主应力增大，ε1和ε3增大，σ2方向因受约束，ε2曲线斜率增大，εV曲线表现出负向弯曲趋势；在卸荷过程中，粉砂岩变形模量随卸荷量增大而减小，近似呈负指数形式变化。

3)粉砂岩真三轴卸荷峰值强度与中间主应力关系拟合曲线用二次多项式表示较准确；Mogi-Coulomb强度准则的线性拟合效果较好，且回归方程满足显著性水平α=0.01的F检验要求，所以，使用Mogi-Coulomb准则能较好地反映粉砂岩真三轴卸荷破坏强度特征。