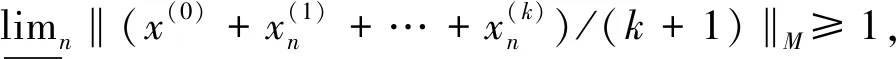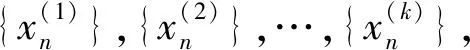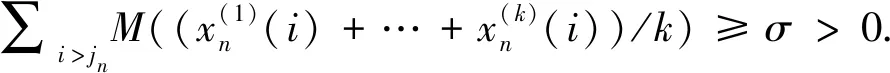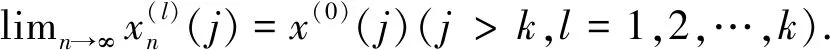赋Luxemburg范数的Orlicz序列空间的k一致凸点
段丽芬,左明霞
(1.通化师范学院数学学院,吉林 通化 134002;2.哈尔滨理工大学理学院,哈尔滨 150080)
众所周知,Orlicz空间的引入不但丰富和完善了Banach空间理论,而且带动了不动点[1]、逼近论[2]、微分方程[3-4]等领域的研究.而不动点性质很大程度上取决于所在空间的性质,所以在Orlicz空间发展过程中,与不动点有关的几何性质(如: 一致非方[5]、一致凸[6]、k一致凸[7]等)一直备受关注.作为k一致凸概念的直接推广——局部k一致凸也自然成为研究的热点,局部k一致凸Banach空间的特点也随之日渐清晰[8-9].关于Orlicz空间,其局部k一致凸和Orlicz函数空间局部k一致凸点的判据均已获得[10].本文拟采用处理序列空间的特殊技巧,研究赋Luxemburg范数Orlicz序列空间的k一致凸点,讨论该空间单位球面上点为k一致凸点的判别准则.
1 定义及符号
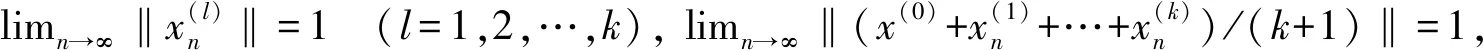
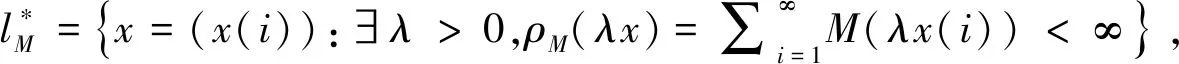
2 主要结果
定理1设M是N-函数,x(0)=(x(0)(i))∈S(lM)是k一致凸点的充要条件为: i)M∈Δ2;ii) 若μI≥k,则M∈2且{x0(j)|j∈NI}∩(∪i[ci,di))=φ,其中I={j∈N:|x(0)(j)|∈∪i(ai,bi]};(ai,bi],[ci,di)为M的线性区间.
证明 必要性: Banach空间单位球面上k一致凸点为k强端点,故M∈Δ2成立[11],只须证明ii)即可.
(a) 设I={1,2,…,k},j=1,2,…,k,当u∈[x(0)(j)-εj,x(0)(j)]时,不失一般性地设M(u)=Aju+Bj,其中常数Aj,Bj,εj>0,D=Ajεj.假设M∉2,则存在正数列un↓0,使M(un)<2-n,M(kun/(k+1))>(1-1/n)kM(un)/(k+1),n=1,2,….取正整数mn,有D-2-n≤mnM(un) (b) 假设存在j>k,|x(0)(j)|∈[c,d),当u∈[x(k+1),x(k+1)+ε]时,不失一般性地设M(u)=Au+B,且Aε=D.定义x(l)=(x(0)(1),…,x(0)(l-1),x(0)(l)-εl,x(0)(l+1),…,x(0)(k),x(0)(k+1)+ε,x(0)(k+2),…)(l=1,2,…,k),则类似可得A(x(0),x(1),…,x(k))≥ε1ε2…εk>0,矛盾. (b) 当μI≥k时,不妨设I={1,2,…,k},M∈2且{x0(j)|j∈NI}∩(∪i[ci,di))=φ,则 (1) (i) 若存在j∈{1,2,…,k},不妨设j=k,使得x(0)(k)∉∪i[ci,di),则x(0)(j)∉∪i[ci,di)(j≥k).类似于(a)的证明便可得结论. 定理2设M是N-函数,lM是局部k一致凸的充要条件是(i)M∈Δ2且M在[0,M-1(1/(k+1))]上严格凸;(ii)M∈2或M在[M-1(1/(k+1)),M-1(1/k)]上严格凸. 证明 必要性: 因局部k一致凸的Banach空间必然是k严格凸的,所以(i)成立[11]. 若(ii)不成立,即M∉2且存在M的线性区间[a,b]使得M(a)<1/k,则存在u∈(a,b]和v>0,满足M(u)<1/k,kM(u)+M(v)=1.记则x∈S(lM),但由定理1推知x不是lM的k一致凸点,这与lM是局部k一致凸矛盾. 充分性: 当M在[M-1(1+1/k),M-1(1/k)]上严格凸时,则对任何x(0)=(x(0)(i))∈S(lM),皆有μ{j∈N: |x(0)(j)|∈∪i(ai,bi]}