自由电磁场理论的量子规范变换和生成元判据
孙为民
(南京大学物理学院,江苏南京210093)
核子自旋结构问题的研究,自20世纪80年代后期发轫以来,在实验与理论的交互推动和促进下有了骄人的发展[1],在高能物理现象学界,形成了“高能自旋物理”独特的小型专业领域。JI[2]的原创性基础研究首次给出了核子自旋的规范不变分解方案,多年来,此方案被学界公认为最标准的分解形式,指引着自旋物理的研究方向和工作脉络。2008 年,CHEN 等[3]提出并建立了一种新的、完全QCD意义的核子自旋分解的整体性方案,在自旋物理领域引发了一股热潮[4-5]。 此后,研究者从不同角度,改进和发展了CHEN等的方案,并提出不同的意见和看法,极大地丰富了现有的知识结构与理论体系。其中LEADER[6]独树一帜,认为CHEN等[3]坚持的“规范不变性”完全没有必要,现实规范理论中,甚至连一个物理系统的总动量、总角动量算符也并非规范不变的。因此,他认为坚持“规范不变性”的分解原则是多余和不足取的,在构造一般意义的动量、角动量分解方案时,最基本的要求是“各部分的动量、角动量算符”是“相应的粒子场算符的平移、转动生成元”。据此提出最原始的“正则形式”的总动量和角动量分解方式才是自然和物理上唯一正确的。此后,CHEN[7]回应并指出,如果定义与考虑“物理的规范场、费米子场”算符,那么,文献[3]中的“动量、角动量算符”自然也满足这一“生成元判据”。文献[7]讨论的情形,实质上是限于所谓的“库伦规范”的 GIE(Gauge invariant extention,规范不变扩展形式),从数学角度看,这种所谓的“物理场”算符,就是通常所说的“Dirac变量”。文献[4]认为,对于一般的 GIE(即推广的Dirac变量),这种“生成元判据”自然是满足的。因而,这一点似乎已经有了“定论”。
本文将重新探讨这一问题。事实上,“生成元判据”的检验,需用到量子化场算符的“等时对易关系”,而在规范理论中,选择不同的量子化规范,会有不同的“算符等时对易关系”,产生的Hilbert空间都不一样。Dirac变量(也就是GIE)是规范不变的,它们之间的“等时对易关系”,也不一定就是“标准形式”。 然而,文献[4]却完全默认了这一点,自然认为这种“生成元判据”一定满足物理场。原则上,应从特定规范下的算符量子化方案出发加以检验。规范场理论对一般规范条件下的(算符)量子化形式无统一的处理方法,通常是对给定形式做特定的讨论。一般而言,任意2种不同规范下的量子理论的联系,即所谓的“量子规范变换”,是非常困难的,早在 20世纪 70年代,STROCCHI等[8]就提出了基本理论框架,描述了“量子规范变换”的构造语言,其中讨论的是量子电动力学,但并未得到一般情形的显式构造。本文将针对检验规范场理论中“生成元判据”的基本问题,在最简单的“自由电磁场理论”中,选取一类较普遍的“静态规范”作为实例,采用构造性方法,建立从“库伦规范”到“静态规范”的“量子规范变换”。然后,讨论新规范下的自由电磁场量子理论,包括 Poincaré群生成元的具体构造,并检验这种生成元判据的正确性。主要工作包括两部分:首先,建立理论构造的基础,对于电磁场的量子理论,本文所得的构造形式是新的;然后,用此理论具体分析“生成元判据”问题。本文讨论的是最简单的规范场系统,即自由电磁场,结果表明,这种“生成元判据”的成立依赖于具体的“规范条件”,即特定 GIE场的“定义条件”。本文工作对规范场理论以及核子自旋结构研究,均有一定的参考作用。
1 量子规范变换基本形式
本节的主要目的是建立“量子规范变换”的构造形式。 首先,依照文献[4]的观点,即规范势Aμ的“规范不变扩展”,将某一特定“经典规范条件”下的Aμ用场强Fμν表达(往往是一个非定域形式的积分表达式),使其成为“规范不变式”,与“洛伦兹不变扩展”类似。比如,一个相对论性粒子的“静止质量”平方满足:pμpμ=m2,从任何一个惯性参照系(假定考虑狭义相对论的平直闵可夫斯基时空)中看都是不变的。 GIE的基本实例,即“库伦规范GIE”。 库伦规范条件:∇iAi=0,可以唯一确定规范势Aμ(只要加上物理的边界条件:Aμ(x,t)||x|→∞=0),利用Fμν= ∂μAν- ∂νAμ,就可以得到库伦规范中的电磁势

式(1)称为“库伦规范 GIE”。 在自由电磁场情形下,式(1)可化为

其中,A⊥i是矢量势Ai的横向部分。在核子自旋结构问题的研究中,提出了多种GIE形式,有“光锥规范条件”A+=0的 GIE,“轴规范条件”A3=0的GIE等[9]。这些都是为特定目的设计的。在LEADER提出的规范场理论中,认为动量、角动量算符分解的“生成元判据”是“适用于物理的规范场和费米场算符”的,因而是正确的。这里的“物理场”等同于数学上“推广的 Dirac变量”,其实,就是GIE表达式,即“规范不变的场”。在特定规范条件(即GIE的“定义条件”)下,自然回到了原有的Aμ场。本文工作中,笔者试图从根本上进行检验,则需要研究由“GIE算符”出发的生成元算符的构造,及其之间的基本对易关系。GIE场事实上代表了特定规范下的规范势,因此,需要从这一类特定规范下的“量子规范理论”出发进行讨论。
STROCCHI等[8]所建立的理论框架为量子电动力学的“量子规范变换”提供了一种普遍性的语言,但他们并未给出任意2个“规范条件”下相应“量子电动力学理论”之间明显构造性的联系形式。本文将在一定意义上,从标准的库伦规范到较为广泛的“静态规范”之间,针对自由的电磁场理论建立“量子规范变换”的明显构造形式,并讨论这类“静态规范”下的量子化电磁场理论,包括Poincaré变换生成元的具体构造方式,从而明确回答了“生成元判据”是否成立这一问题。
“静态规范”是指这一形式的“线性规范条件”:PiAi=0,其中,Pi=(P1,P2,P3)是一个三分量的常数或微分算子,不包含对时间变量的微商运算,要求Pi中不显含时间或空间坐标(从而排除了Poincaré规范x⋅A=0这类情形),目的是保持整体理论表述形式的时空平移不变。
特定规范下的GIE,实质上就是此规范下的Aμ场。PiAi=0规范下的APμ场,同库伦规范∇iAi=0下的ACμ场,由于对应于同样的场强Fμν,两者之间,必然相差一个标量函数的四维梯度[10]:
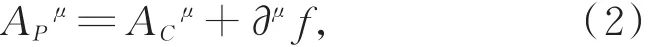
其中,标量函数f(x)实质上是依赖于场位形的。取式(2)的空间分量:,再由条件,就有

式(3)为决定未知函数f(x)的一个非齐次偏微分方程,可用标准的格林函数法求解,得到


具体采用哪一种格林函数,由边界条件决定。于是,有

类似地,由

得

最后,有

接下来建立“静态规范”PiAi=0下的量子场理论。规范场量子化问题的讨论,实质是独立自由度的考虑和量子场Hilbert空间的建立。通常在库伦规范量子化中,只有2个横场自由度被量子化,生成的Fock空间,只包含横极化光子态,而在洛伦兹规范量子化中,Aμ的4个分量皆被量子化,生成的量子态 Fock空间中,包含4种极化光子,且具有不定度规。
借助经典场意义的对映关系式(5)和(7)来构造PiAi=0规范下量子理论的基本思想。若库伦规范势ACμ中包含2个横向的物理自由度,那么,由式(5)和式(7)所构造的APμ亦如此。 既然,物理自由度数目一样,那么,可以直接在原有的“库伦规范的Fock空间”上,建立“新规范PiAi=0”的量子理论。下面将进行具体描述。
取定库伦规范量子化的Fock空间。此Fock空间有唯一的真空态和一套完整的横场算符的集合。理论上,任何一个物理态都可由场算符的多项式作用于真空态而得到。定义一种新的量子规范势算符APi:

这在数学上无疑是正确和可接受的,从物理意义看,无非是从原有的库伦场出发定义了一套新的场,是在场算符的意义上而非经典场函数的意义上定义的,此过程自然保证满足“算符规范条件”:0。 注意,此过程没有改换 Hilbert空间,即Hilbert空间始终没变,只是定义了一套新的场,满足另一种“规范条件”罢了。再定义:

于是,一套完整的“规范势算符”APμ(x)构造成功。
以上便是本文工作基础构造的出发点。虽然,规范条件PiAPi=0的形式有无穷多种选择,原有的库伦规范Fock空间上,就有无穷多套新规范势算符APμ,但其对应的“场强算符”却完全相同,均为
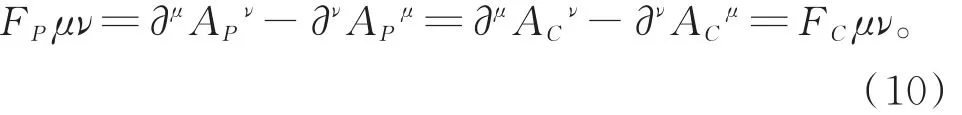
先看场算符之间“等时对易关系”的形式。库伦规范量子化中,共轭场变量为(AiC,EiC),其中电场为其间的标准等时对易子为

利用式(8),同时记EPi=ECi,可得


注意到,式(16)右端不再是标准的“三维横向Diracδ函数”形式,这是因为需要与“算符规范条件”PiAPi=0相一致。在一般的静态规范下,有可算出之间的等时对易式。利用式(8),就可得


其中,仅涉及横波极化和相应的自由光子态的产生湮灭算符。由式(8)可得


式(19)为“扭曲的平面波展开”式。
下面讨论新的量子化方案(规范条件PiAi=0决定的量子化形式)的定域性问题和微观因果性问题。众所周知,库伦规范下电磁场的量子化理论不是“定域”的,对任意2个时空点x,y,有


显然,一般情形下,此“对易子函数”对于类空间隔的两点也是非零的。因此,新规范下的理论也是非定域的。但是,与库伦规范相同,电磁场场强算符在类空间隔两点处总是对易的,则新规范下的理论也满足“微观因果性”的要求。
接下来,讨论 Poincaré变换生成元。 原有的“库伦规范”量子化中,理论上Fock空间承载了Poincaré群的一个无限维幺正表示。有10个守恒的 Poincaré群的生成元算符,即能量算符(哈密顿量算符)、动量算符、角动量算符、boost生成元算符等。在规范场理论的动量与角动量分解问题中,笔者关心的是动量、角动量算符。下面先构造哈密顿算符,因为,依照形式场论的观点,哈密顿算符应该是理论上的时间平移生成元。
因物理自由度仍是2个,Hilbert空间也没有变动,依据“规范不变性”的要求,有


由式(8),有


由式(8)的变换关系,易得

本文的理论构造,实质上就是在库伦规范量子化的Fock空间上,复制出一套“静态规范”0的自由电磁场量子理论。由于规范条件0的形式无限多,因此相应的“理论复本”也有无限多个。比如,可取“扭曲的库伦规范”:cij∇iAj=0,其中cij是一组数值系数,满足对称性要求:cij=cji,这类“规范条件”由cij来标记。其实,如果数值系数连续变化,“规范条件”样式就是连续的流形,若允许有更多的选择,整体结构会异常丰富,而所有“规范理论的复本”都是定义在原库伦规范的Hilbert空间上的。因此,可讨论从一种“理论复本”到另一种“理论复本”之间的过渡,或曰变换。很明显,这种两两变换的体式,形成了一个“变换群”,与前文的讨论结果一样,这种变换不是通过Fock空间上的幺正变换来实现的。无论从数学角度还是量子规范场论角度看,这样的研究都是有意义的。
2 生成元判据
文献[4]所言的“物理的规范场”,其实就是GIE场。从横场算符的角度看,库伦规范场ACi是“规范不变的”,依据式(8)和式(9)的构造,新的场,也是规范不变的。前文已经建立了量子化的理论要素,这里研究“自由电磁场”,因此,不存在“分解问题”(除总角动量分解为轨道和自旋部分外),需要说明的是,即便是“整体的动量、角动量算符”,也有非平凡的现象出现。
先看“动量算符”。在原有的库伦规范中,有

式(29)反映了理论空间平移不变的特点。规范条件PiAPi=0的构造式中,Pi是不显含时空坐标的,因此,此“规范条件”是空间平移不变的。利用式(8)中的构造,可得

于是,动量算符P同样也起着APi场的空间平移生成元作用。
再分析“角动量算符”。 库伦规范中,ACi(x)是三维矢量场算符,满足“生成元关系”:

那么,对于APi场,类似的关系式满足吗?从物理学角度看,从现有的ACi场出发,由式(8)的定义,给出场。因此,在相同的“量子场Hilbert空间”上,可由式(8)得到对应的“生成元变换式”。 注意,式(31)之所以成立,是因为ACi是转动的三维矢量。若由式(8)所定义的APi场是一个三维矢量场,则同样有否 则 必 有由 式(8),有因 此 ,只 有 当Pi=(P1,P2,P3)是一个真正意义的“三维矢量”时,才可说APi是一个真正转动的“三维矢量场”。库伦规范条件∇iAi=0无疑是符合这一要求的,但任意构造的“静态规范”PiAi=0往往不满足此条件,如“轴规范条件”A3=0,前文所述的“扭曲的库伦规范条件”cij∇iAj=0。
至此,可以得到结论:文献中的“角动量算符生成元判据”在“静态规范”的自由电磁场情形下,通常是不满足规范条件的。
那么,这一结论的物理意义是什么?前文已述,库伦规范的Fock空间架设了Poincaré变换群的无限维幺正表示,所以,10个 Poincaré群生成元算符有良好的定义,由式(8)和式(9)的构造性定义可以指明新的APμ(x)场算符的洛伦兹变换方式:若Pi=(P1,P2,P3)非真正的三维矢量,那么规范条件PiAi=0就不是“空间转动协变”的,此情形可类比于“库伦规范”∇iAi=0中的讨论。库伦规范条件是“空间转动不变的”,但在boost变换下,却非协变的,因此,在一般的boost变换下,可以定义标准的“boost生成元”算符,但不再满足“标准的boost算符同真正四维矢量场的对易式”。事实上,在一般的boost变换下,库伦规范势ACμ“先做一次标准的boost,再继续上一次附加的规范变换”,以保证在新的惯性参照系中,库伦条件满足:∇´iA´i(x´)=0。同样,当规范条件PiAi=0明显非转动协变时,对易关系式[Ji,APj]的具体形式(偏离了“三矢量变换”的标准形式)恰好表明,在三维空间转动下先做一次标准的“矢量转动”,再做一次“附加的规范变换”,以此,在转动后的新坐标系中,恢复“非协变的静态规范”:PiAPi=0。
于是得到,在自由电磁场情形下,由于GIE条件的多样性,即便对“物理的规范场”,通常也未能满足文献中所提出的“角动量算符的生成元判据”。
3 总结与展望
针对自由电磁场理论,建立了从库伦规范到特定“静态规范”的“量子规范变换”。这种显式构造,令“静态规范”下量子理论的结果更为充分与丰富。本研究可进一步推广,如当“规范条件”PiAi=0未能“唯一确定规范”时,本文所构造的“静态规范”下的量子理论其实是不唯一的,当PiAi=0条件下无法唯一确定规范时,相应的经典场方程(3)不能唯一确定“规范变换函数”f(x),于是,相应的量子场算符AμP(x)的构造方式就不唯一。本文只选择了一种最简单的构造形式,PiAi=0条件下的剩余规范自由度如何影响理论构造,有待进一步研究。
关于“生成元判据”,虽然本文只检验了“自由电磁场”的情形,但其物理问题的实质是清楚的,即如果“静态规范条件”PiAi=0不是“转动不变的”,相应的“物理场”算符就不满足标准的“转动生成元关系”。原则上,可做类似推广,但“生成元判据”成立的基础,即“规范条件”(GIE的定义条件)的转动变换不变性,不会改变。笔者期望在将来的工作中,这一问题有更明确的结论,包括由这一理论框架向非阿贝尔规范场情形的推广。

