我国地理可照时数空间分布模拟中尺度效应研究

李军 ，黄敬峰 ，龚围 ，王超 ，李冰

（1.重庆师范大学地理与旅游学院，重庆401331；2.重庆市高校GIS应用研究重点实验室，重庆401331；3.三峡库区地表过程与环境遥感重庆市重点实验室，重庆401331；4.浙江大学农业遥感与信息技术研究所，浙江 杭州 310029）

地理可照时数（duration of possible sunshine，简称PSD）是仅考虑地形和地理因子影响不考虑云雾影响时日出到日落的太阳照射时间，是地表辐射平衡、生态系统模型等的重要参数之一[1-2]，也是我国太阳能资源计算和评估的重要指标之一[3]。地理可照时数空间分布研究对于我国山地气候和农业气候资源区划及其开发利用、生态系统基础信息的空间化研究等具有重要意义[4-5]。

我国地域辽阔且多山，其中，南北纬度从4ºN到50ºN，跨度非常大，而且，山地面积约占国土总面积的三分之二，海拔从吐鲁番盆地的艾丁湖（－154 m）到珠穆朗玛峰（8 848 m），跨度非常大。受纬度、海拔、坡度、坡向等因素的影响，地理可照时数的空间异质性非常大。我国对于起伏地形下地理可照时数等太阳辐射要素的空间分布研究始于20世纪80年代初，以左大康[1]、翁笃鸣等[2]、傅抱璞等[4-5]、朱志辉[6]、李占清等[7]等为代表的学者，提出了不同的理论模型和算法，奠定了日后基于DEM的地理可照时数及其太阳辐射要素空间分布模型的理论基础。其中，对于地理可照时数，通常利用解析法或图解法确定，然而，不同地形有不同的解析算法，非常复杂，图解法相对容易，但其内外业工作相当繁琐，且精度不高。国外，DOZIER等[8]于20世纪70年代末首次在地形参数快速算法的基础上提出了基于DEM的太阳辐射空间化方法。之后，以BOCQUET等[9]、DUBAYAH 等[10]、DOZIER 等[11]、HETRICK 等[12]、KUMAR 等[13]、DANIEL 等[14]、PINDE 等[15]为代表的学者们开展了基于DEM的不同太阳辐射要素空间分布模拟及其与不同地形因子的定量关系研究。目前，由于全球高空间分辨率数字高程模型（DEM）数据的免费获取和数字地形分析的深入应用，基于DEM的地理可照时数等太阳辐射要素空间模拟算法已趋于成熟。

我国学者在此方面的研究始于20世纪90年代初，利用不同空间分辨率的DEM数据在不同区域进行了应用研究。例如，李新等[16]修正了基于DEM的日照时数空间分布模拟方法。谢阳生[17]在ViewGIS平台实现了可照时数等太阳辐射要素空间分布模型，并在宁夏西吉县的小流域进行了试验应用。陈华等[18]基于1：50 000数字化地形图得到了100 m分辨率的DEM，并在此基础上对北京西山门头沟区可照时数的空间分布进行了模拟。曾燕等[19]利用1 km分辨率的DEM数据并基于PCI的二次开发程序，实现了我国可照时数空间分布的模拟，并探讨了其受不同地形的影响。李军等[20]以20 m分辨率的DEM数据（源于1：10 000数字化地形图）为基础定量分析了浙江省仙居县可照时数的空间分布特征。孙娴等[21]基于100 m分辨率的DEM数据，考虑了坡度、坡向和地形遮蔽等地形因子对可照时间的影响，通过数值模拟，建立了陕西省山地可照时间的计算模型。潘用地[22]对起伏地形下日照时间-空间分布模型进行了修正，并检验了计算精度，其中，所用DEM数据的空间分辨率为90 m。张超等[23]利用基于DEM的起伏地形下实照时数的计算模型，以广西省巴马县为例，对其可照时数的空间分布进行模拟，采用的DEM为ASTER GDEM，分辨率约为30 m。由上述研究可知，在基于DEM的地理可照时数空间分布模拟中，DEM数据是重要的输入参数，对模拟结果的影响很大，由于DEM的格网间距不同，即空间分辨率存在差异，而分辨率是尺度的一个指示器，DEM的这种尺度效应导致其对地形的反映也存在差异。一般情况下，DEM的空间分辨率越小，其精度越差，对真实地形的概括程度越低，特别是坡度、坡向等微地形因子的误差越大[24]。针对研究区特点，选择合适的DEM是进行太阳辐射和气温等气象要素准确模拟的基础。其中，DEM的空间尺度是起伏地形下可照时数模拟结果差异的重要根源之一。目前，关于这方面的研究相对较少，张勇等[25]改进了日照时间计算模型，并在全国选取了6个典型地貌区进行了相关研究。但采用DEM的空间分辨率为500 m和1 000 m，相对较粗，对于地形复杂且较破碎的山区不能准确定量分析。姜创业等[26]利用1：250 000 DEM数据，从100 m和1 000 m 2种空间分辨率尺度，分析了DEM的空间尺度效应对陕西省天文辐射的影响。周文臻等[27]基于ASTER GDEM和SRTM 2种DEM数据源从30，90和1 000 m 3种空间分辨率尺度，分析了DEM对福建省天文辐射的空间尺度效应的影响。由于应用的区域相对较单一，分析DEM空间尺度效应对天文辐射的影响，其参考价值有限。

综上所述，考虑目前应用较广泛的3种DEM数据源、研究区范围大小以及数据计算量等诸多因素的影响，在全国选取6个典型地貌类型区为实验区，利用3种不同空间分辨率的DEM数据（分别源于GTOPO30´、SRTM 和 ASTER GDEM 数 据库）模拟起伏地形下不同空间尺度的地理可照时数分布，并定量分析它们之间的差异以及不同地形因子对模拟结果的影响。

1 实验区和不同空间尺度的DEM

1.1 实验区

根据我国陆地主要山脉的空间分布以及地形地貌特点，主要考虑山脉走向、纬度和地形起伏等因素，选取了6个实验区（见图1），分别为小兴安岭（编号：1）、太行山区（编号：2）、秦岭（编号：3）、青藏高原弧形山区（编号：4）、横断山区（编号：5）和东南丘陵（编号：6）。

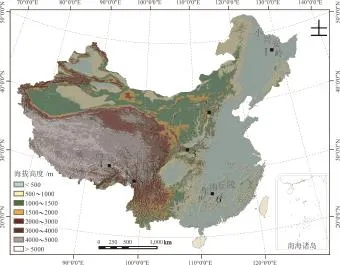
图1 全国6个实验区的地理位置Fig.1 The geographical location of six study areas throughout the country

每个实验区面积为2 916 km2（54 km×54 km），区域范围见表1。

1.2 不同空间尺度的DEM数据

分 别 从 GTOPO30´、SRTM v4.1 和 ASTER GDEM v2三种全球DEM数据库中截取得到上述6个实验区的DEM数据，并进行重采样，得到空间分辨率分别为900，90和30 m的6个实验区的DEM数据，其中，30 m空间分辨率的地貌晕渲图见图2。

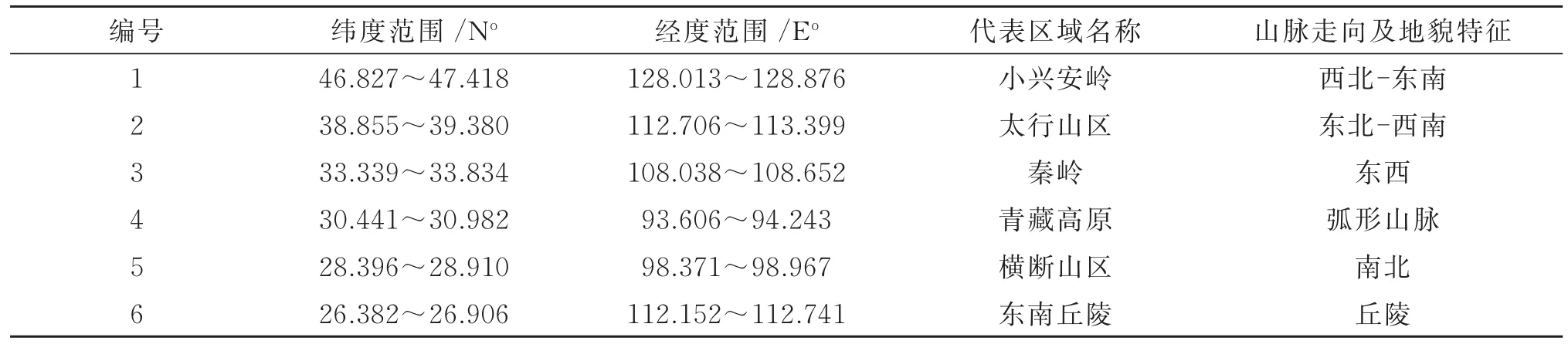
表1 实验区的地理区域范围Table 1 The geographic range of six study areas in China

2 地理可照时数分布式模型

2.1 起伏地形下的地理可照时数

根据左大康[1]、翁笃鸣等[2]的研究，起伏地形下，地理可照时数可表示为：

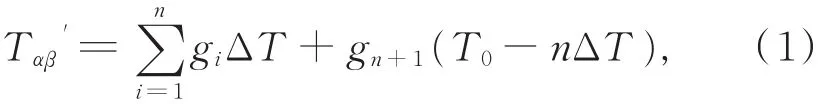
2.2 基础参数

关于起伏地形下地理可照时数分布式模型中基础参数计算的说明如下：

图2 实验区30 m空间分辨率的地貌晕渲图Fig.2 The geomorphologic map with 30 m resolution in study areas

（1）水平面的可照时数（T0）：可由式（2）得到：

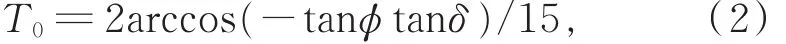
其中，φ为纬度，δ为赤纬。

（2）太阳赤纬（δ）：基于相关研究[28]，通过傅里埃级数展开得到：

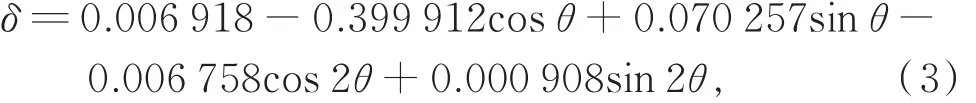
（3）地形遮蔽因子（gi）：起伏地形下一天内任意时段i的遮蔽情况取决于相邻两时刻的遮蔽情况。若相邻两时刻均可照，则此时段可照，地形遮蔽因子取1；若相邻两时刻均遮蔽，则此时段遮蔽，地形遮蔽因子取0；若相邻两时刻中某一时刻可照，而另一时刻遮蔽，则此时段的地形遮蔽因子取0.5。其中，任一时刻的地形遮蔽情况可利用ArcGIS的山体阴影函数得到：

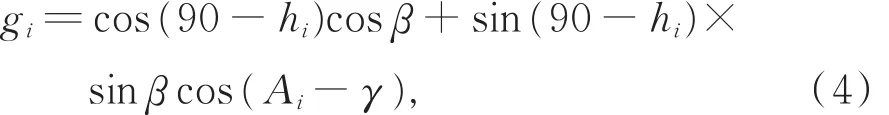
其中，β和γ分别为坡度和坡向。只要输入坡度、坡向以及任一时刻太阳在天空中的位置（太阳高度角和太阳方位角）即可，由此可见，地形遮蔽对地理可照时数的影响取决于坡度、坡向、太阳高度角和太阳方位角。

（4）任一时刻的太阳时角（ωi）及其对应时刻的太阳高度角（hi）和方位角（Ai）：

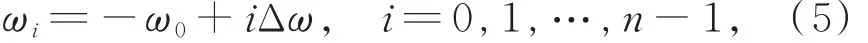
其中，-ω0、ω0分别为日出和日落时的太阳时角，ω0=arccos(-tanφtanδ)；Δω为时 角 步 长 ，Δω=

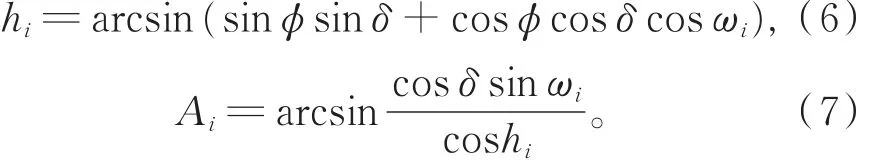
（5）时间步长（ΔT）：时间步长越短，计算精度越高，但计算时间越长。根据李占清等[7]的研究，时间步长取20 min和1 min时两者的计算结果仅差5%，本研究在综合考量计算量、计算时间和计算精度后，将时间步长设为20 min。

3 地理可照时数的不同空间尺度模拟

在起伏地形下的地理可照时数分布式模型中，输入DEM和相关地形因子等参数，利用ArcGIS的空间数据叠加运算等，可得到任何一天的地理可照时数，月或年的地理可照时数可通过逐日累加得到；气候学的相关论述表明：常取每月的第15日为代表日，并乘以当月天数作为该月的地理可照时数。限于篇幅，仅列出30 m空间分辨率实验区1月份的模拟结果（冬季的太阳高度角较小，地形影响更显著），如图3所示。

从图3可看出，地形对我国不同区域1月地理可照时数影响的差异显著，利用ArcGIS对空间数据分别进行统计，分析了6个实验区的中心纬度、海拔高度、地形起伏度、坡度、地形阴影、地表粗糙度、平面曲率、剖面曲率以及1月和7月地理可照时数特征值（平均值和标准差），其中，地形起伏度的邻域范围借鉴基于ASTER GDEM数据的相关研究，统计单元采用59×59的网格大小[29]。地形阴影采用基于ArcGIS的山体阴影算法（Hillshade函数）计算，其值为0～255的整数灰度值，值越小（颜色越暗）表明地形遮蔽越强，为了体现地形阴影值越大，地形遮蔽越强的特点，将255-Hillshade作为地形阴影值，此外，计算时太阳高度角和方位角分别取45º和135º，接近于一天的平均值时刻。地表粗糙度表示特定区域内地表面积与投影面积的比值。剖面曲率和平面曲率分别为地形表面在垂直和水平方向上扭曲变化程度的度量因子。各项特征值的统计结果见表2。

由表2可知，我国不同区域的地理可照时数差异非常显著，1月平均值在198.2～297.5 h，差值为99.3 h，标准差 在 20.3～78.5 h；7月平均 值在 323.6～429.1 h，差值为 105.5 h，标准差在 18.2～40.9 h。7月变化的绝对差异略大于1月，但相对差异小于1月，这主要是由于冬季太阳高度角较小，地形遮蔽影响更显著，空间异质性更大。造成地理可照时数差异的因素很多，从其分布式模型可知，主要有海拔、纬度、太阳赤纬、地形遮蔽等因子，这些因子均与地理位置和地形紧密相关，基于30 m DEM统计了各实验区有代表性的地理和地形因子特征值以及1月和7月可照时数（见表1），分析其间的关系，发现：影响1月、7月地理可照时数及其差异的因子分别为剖面曲率、海拔高度、纬度、地形阴影和地形起伏度，其中，1月地理可照时数随纬度、海拔高度、地形起伏度和地形阴影的增加而减少，随剖面曲率的增加而增加；7月地理可照时数随海拔高度和地形阴影的增加而减少，随纬度、地形起伏度和剖面曲率的增加而增加；而冬夏季节的差异和7月具有类似规律。

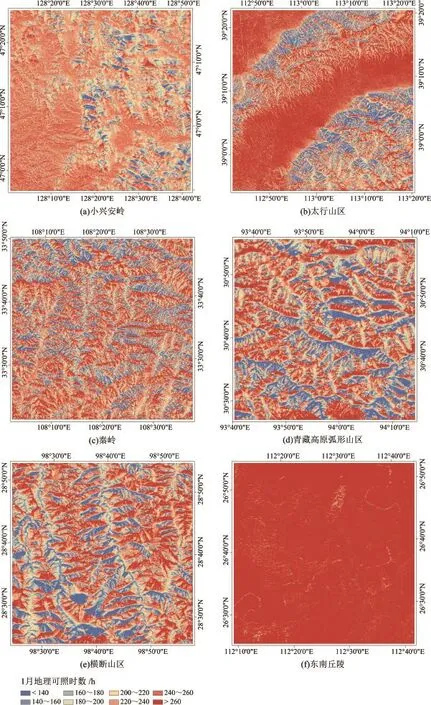
图3 实验区30 m空间分辨率1月份的地理可照时数Fig.3 PSD with 30 m resolution in January in study areas

进一步，在各实验区基于栅格像元进行可照时数与地理和地形特征因子间的多元线性逐步回归统计分析（样本数均为1 800×1 800=3 240 000个像元），结果见表3。

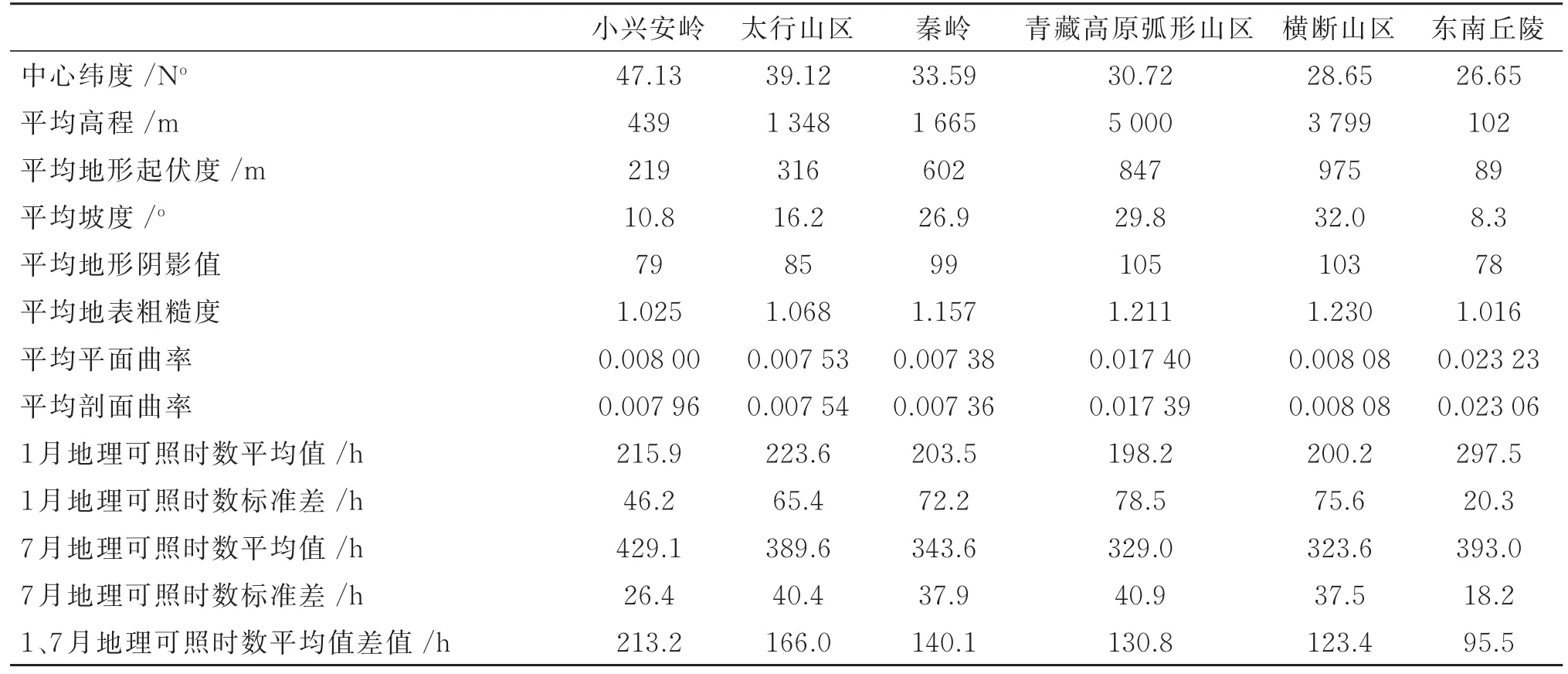
表2 实验区不同地形特征参数以及1月和7月地理可照时数的统计结果Table 2 The statistics of topographic factors and the characteristic values of PSD（mean monthly value and its standard deviation）in January and July in study areas

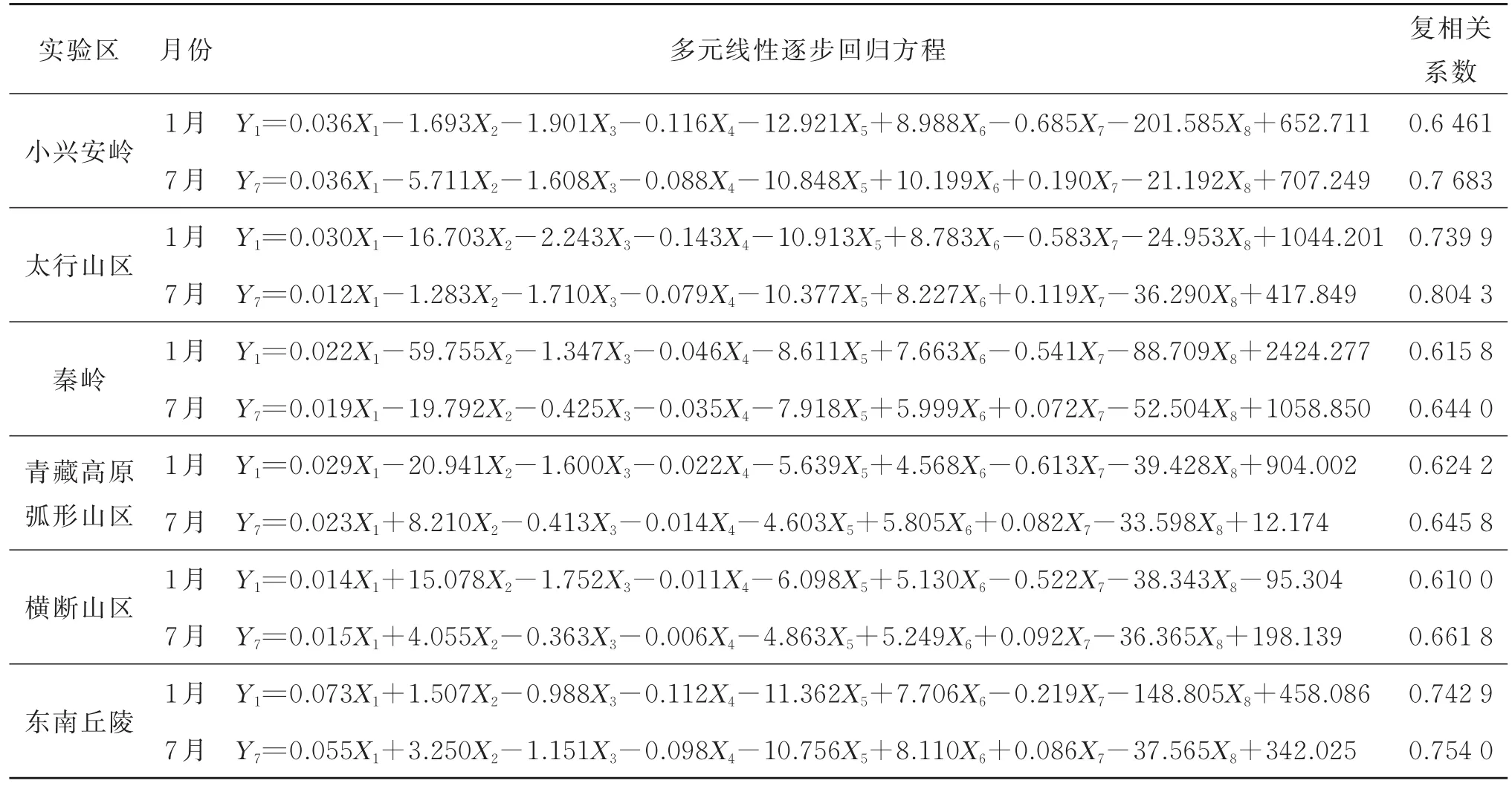
表3 实验区1月和7月地理可照时数与地形特征参数之间的回归关系Table 3 Regression relationship of PSD in January and July depending on topographic factors in study areas

由表3可知，各实验区1月和7月地理可照时数与上述地理和地形特征参数之间的复相关系数在0.610 0～0.804 3，经过信度1%的F检验，均表现为极显著相关，其中，太行山区和东南丘陵地区的相关程度相对较高，而且，同一实验区7月的复相关系数均大于1月；在上述地理和地形特征参数中，始终表现为正相关的为海拔高度和水平曲率，始终表现为负相关的为坡度、地形起伏度、剖面曲率和地表粗糙度，此外，地形阴影在1月表现为负相关，7月表现为正相关，纬度无明显规律。

4 不同空间尺度模拟结果对比

4.1 DEM数据的空间尺度效应

为了定量比较不同空间尺度可照时数模拟结果的差异性，首先，需要分析引起这种差异的重要来源——DEM数据的空间尺度效应，利用ArcGIS对空间数据进行统计分析，得到了基于3种不同空间分辨率DEM数据提取的7个地形特征参数的统计值，结果见表4。纬度空间数据基于每个栅格的地理空间坐标得到，差别很小，所以，未对其进行统计分析。

从表4中可看出：在影响地理可照时数的地理和地形特征因子中，基于不同空间分辨率的DEM提取的平均海拔高度、地表粗糙度和地形阴影之间均相差不大，而且，随着空间分辨率的减小（30 m至900 m），其平均值呈减小趋势，其中，海拔高度的减小幅度最小，其他地形特征因子对空间分辨率均非常敏感，特别是平面曲率和剖面曲率，均随空间分辨率的减小明显减小，其次是坡度和地形起伏度，其中，坡度随空间分辨率的降低而减小，地形起伏度随空间分辨率的降低而增加；针对不同实验区，东南丘陵地区的坡度、水平曲率和剖面曲率的空间尺度效应最明显，而海拔较高的青藏高原弧形山区和横断山区的平面曲率、剖面曲率、地形起伏度、坡度、地形阴影等地形特征因子也存在较显著的尺度效应，其中，地形阴影和地表粗糙度的尺度效应在6个实验区中是最明显的，而坡度的尺度效应却不及海拔较低的小兴安岭、太行山区和秦岭地区。

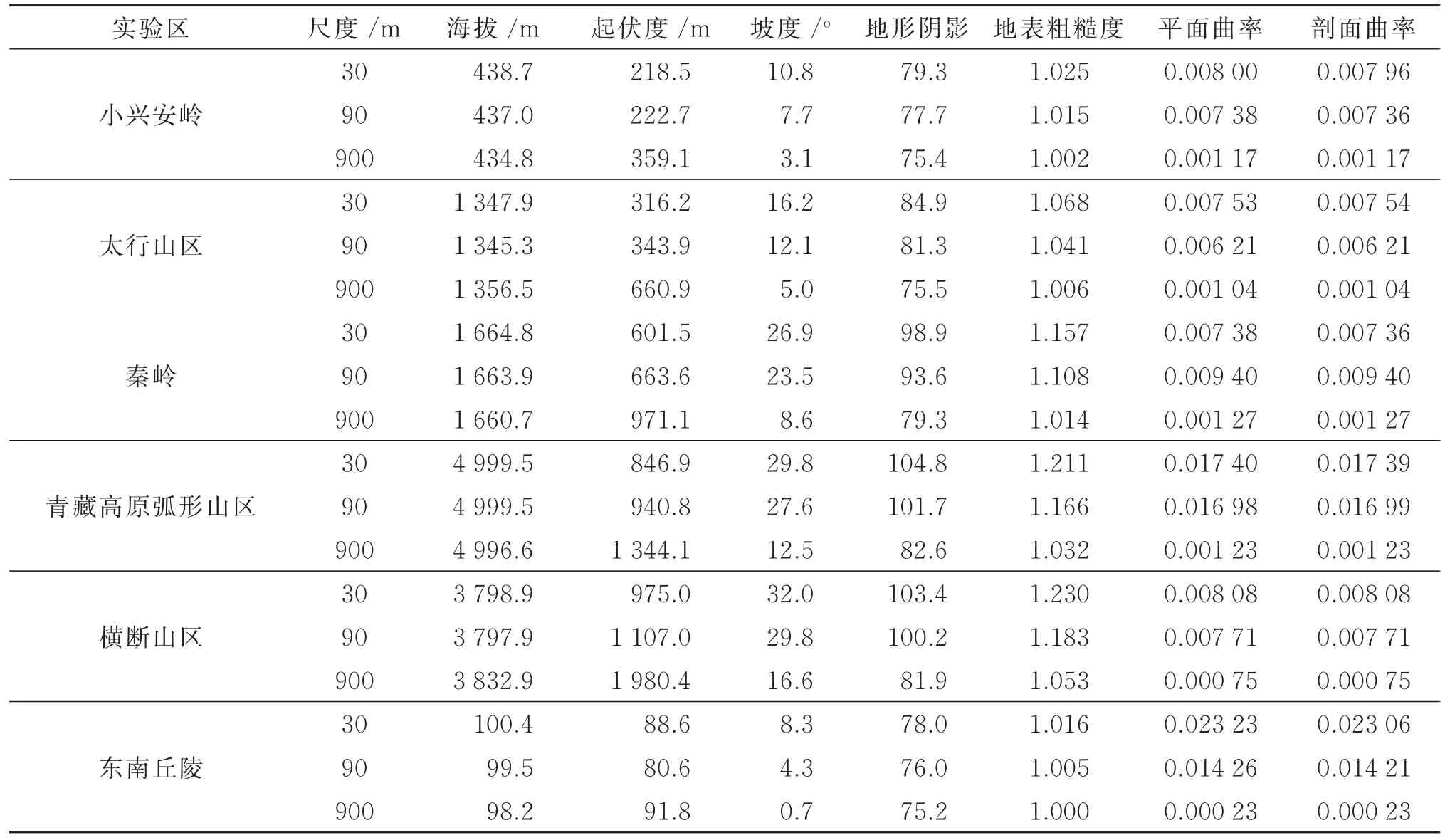
表4 实验区不同空间尺度地形特征参数的统计结果Table 4 The statistics of different terrain factors derived from DEM with three spatial scales in study areas

4.2 不同空间尺度地理可照时数对比分析

为了定量分析地理可照时数不同空间尺度模拟结果之间的差异，利用ArcGIS的空间分析功能，统计了我国不同区域6个实验区不同空间尺度1月和7月可照时数的特征值，结果见表5。

由表5可知：各实验区1月和7月地理可照时数的平均值均随空间分辨率的减小而增大，其标准差均随空间分辨率的降低而减小（空间异质性逐渐降低），1月地理可照时数平均值的增幅均大于7月，其中，青藏高原弧形山区冬夏季的季节差异最大，东南丘陵的差异最小；此外，无论1月还是7月，青藏高原弧形山区地理可照时数平均值增幅均最大（1月从198.2 h增至275.4 h，增加了38.9%，7月从329.0 h增至386.8 h，增加了17.6%），增幅最小的均为东南丘陵地区（1月和7月的增幅分别为8.2%和5.9%）；标准差减小幅度最大的是东南丘陵地区，1月和7月分别达到了89.7%和87.4%。上述不同空间尺度模拟结果的对比表明，DEM空间尺度效应对地理可照时数模拟结果的影响非常明显，随着DEM空间分辨率的降低，对地形表述的准确性减弱，特别是对平面曲率、剖面曲率和坡度等地形特征因子变化的描述明显减弱，标准差和精度明显降低，在本该被地形遮蔽而无日照的区域，其太阳高度角普遍大于地形遮蔽角，使得地理可照时数平均值偏大。此外，由于DEM空间尺度效应引起的地形因子对空间分辨率的敏感性在不同地区表现不同，则对地理可照时数的影响也不同，可根据研究需要和精度要求等考虑DEM空间尺度效应带来的影响。

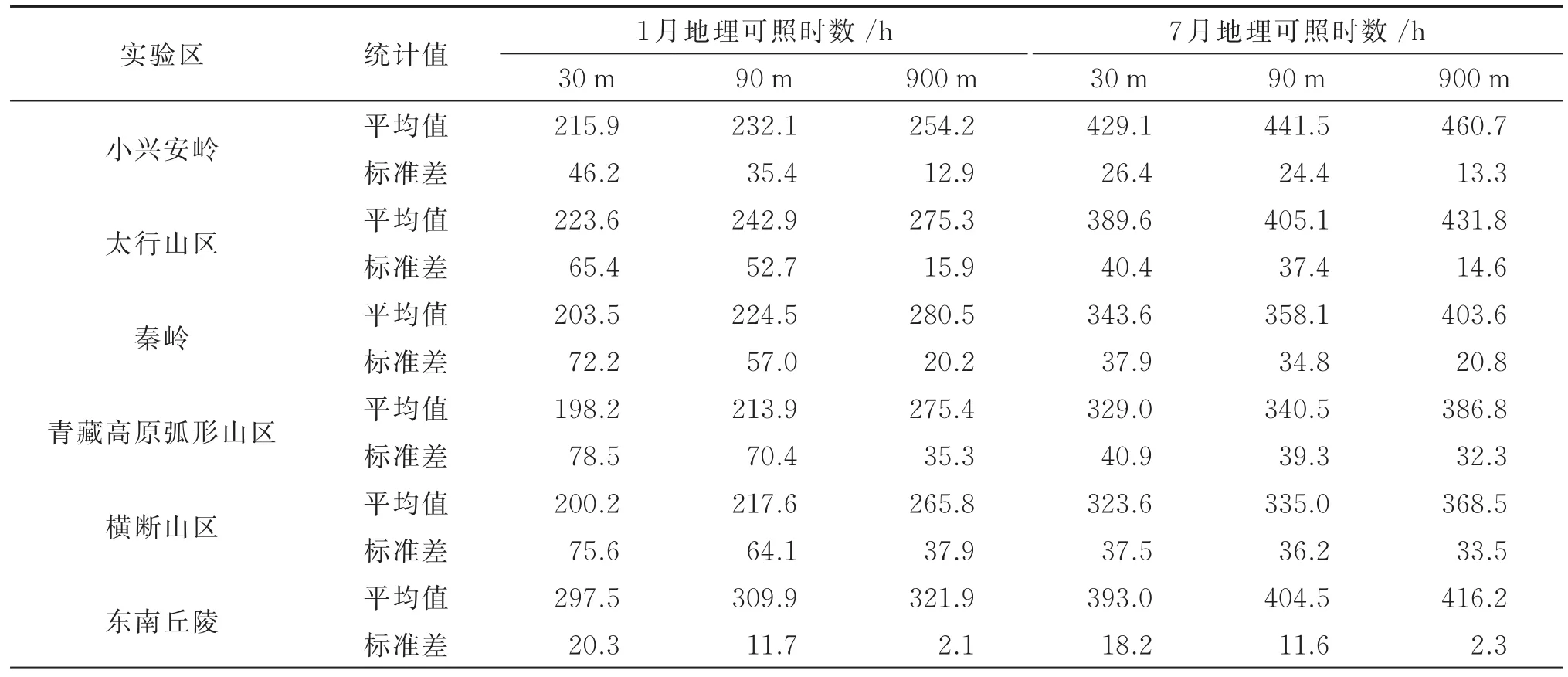
表5 实验区不同空间尺度地形特征参数的统计结果Table 5 Statistics of different terrain factors derived from DEM with three spatial scales in study areas

5 结 论

地形对地理可照时数的影响不可忽视，特别是在地形复杂多样且山区面积广大的我国，在基于DEM的太阳辐射要素空间分布模拟过程中，DEM空间分辨率对模拟结果影响很大，而DEM数据存在一定的空间尺度效应和不确定性。为了分析DEM空间尺度效应对我国地理可照时数的影响，选取6个不同实验区，基于3种不同分辨率的DEM和地理可照时数分布式模型，得到了不同空间尺度的模拟结果，分别进行了对比分析，得到如下结论：

5.1 我国地理可照时数空间分布差异明显，以30 m分辨率模拟结果为例，7月的绝对差异略大于1月，但相对差异小于1月，且受地形影响非常显著，1月、7月及其之间差异的影响因子分别是剖面曲率、海拔高度、纬度、地形阴影和地形起伏度，其中，1月随纬度、海拔、地形起伏度和地形阴影的增加而减少，随剖面曲率的增大而增加；而7月及其与1月的差异均随海拔和地形阴影的增加而减少，随纬度、地形起伏度和剖面曲率的增加而增加。

5.2 实验区1月和7月地理可照时数与地理和地形特征参数之间均表现为极显著相关，其中，太行山区和东南丘陵的相关程度较高，同一实验区7月的相关程度均大于1月；而且，始终表现为正相关的特征参数为海拔高度和水平曲率，始终表现为负相关的为坡度、地形起伏度、剖面曲率和地表粗糙度，此外，地形阴影在1月表现为负相关，在7月表现为正相关。

5.3 地形影响因子中，平面曲率和剖面曲率均对空间分辨率非常敏感，坡度和地形起伏度次之，海拔高度、地表粗糙度和地形阴影相对较弱；但不同实验区存在差异，例如，东南丘陵的坡度、水平曲率和剖面曲率的尺度效应最明显，而青藏高原弧形山区和横断山区的平面曲率、剖面曲率、地形起伏度、坡度、地形阴影均存在较显著的尺度效应。

5.4 地理可照时数不同空间尺度的模拟结果差异显著，各实验区的平均值均随空间分辨率的降低而增大，青藏高原弧形山区在1月和7月的增幅均最大，分别为38.9%和17.6%，东南丘陵增幅最小，1月和7月分别为8.2%和5.9%；此外，标准差均随空间分辨率的降低而减小，空间异质性逐渐降低，而且，冬夏季节差异也随空间分辨率的降低而减小，但不同实验区的表现程度不同，减小幅度最大的是青藏高原弧形山区，最小的是东南丘陵。

5.5 尽管本文给出了不同实验区1月和7月地理可照时数与地理和地形特征参数之间的定量关系，但地理可照时数的影响因子较多，机理复杂，而且，由于数据计算量等的限制，本文选取的区域范围相对有限，后续还需要选取更多、更大的区域进行分析，从而给出不同区域地理可照时数计算中较适合的DEM分辨率建议。

5.6 地理可照时数等太阳辐射要素的模拟较为复杂，但高空间分辨率DEM和数字地形分析功能的应用，使得模拟结果越来越精细和准确。然而，在模拟过程中，DEM的空间尺度效应及其不确定性等对模拟结果产生了较大影响，特别是在地形复杂的山区。一方面，空间分辨率、应用范围、数据计算量、研究目的以及模拟精度的要求等均需要考虑和平衡；另一方面，太阳辐射要素的精细化模拟是气温、降水等其他气象要素准确模拟的基础，因此，其对山区气候和生态环境的评价及其开发利用具有重要意义。